考虑车网耦合的地铁供电系统潮流计算研究

（西华大学电气与电子信息学院，四川 成都 610039）

为合理规划地铁牵引变电所容量和列车发车密度，供电系统设计时需对牵引网进行潮流计算，以获得网压和网流沿线路的分布。当前，地铁供电系统多采用DC750 V 或DC1.5 kV 双边供电方式。学者们对直流供电系统的潮流计算方法进行了研究，主要围绕地铁牵引供电系统建模方法及其解算方法展开。目前广泛使用的牵引供电系统模型可分为回路电流模型[1-2]和节点电压模型[3-7]。回路电流模型仅适用于简单的由接触网、钢轨和回流线组成的系统，常用于计算接触网、钢轨电压、电流等沿接触网纵向分布情况。与回路电流模型相比，节点电压模型适用于复杂拓扑结构的牵引网模型解算，同时适用于现有的其他供电制式下牵引网的模拟计算。

既有的牵引网模型解算方法可分为代数法[1-3]和潮流迭代法[4,7-8]。代数法在牵引网仿真计算初期得到广泛应用，其将电力机车等效为电流源，直接解算牵引网电压、电流的分布。随着交流传动机车和动车组的出现，电流源模型不再符合实际需求，功率源负荷模型逐步替代电流源负荷被应用于牵引网供电计算，其对应的潮流迭代法随之被广泛应用。文献[8]将列车视为功率源负荷，提出了一种基于12 脉波整流机组模型的城市轨道交直流统一迭代牵引供电解算方法。文献[9 -10]提出了地铁供电系统车网联合仿真模型，其中文献[9]将牵引计算的输出结果作为供电计算的输入。文献[11 -12]把逆变回馈装置引入地铁牵引供电系统，将多余的再生能量反馈至高压交流侧，并提出了地铁牵引供电系统建模和潮流计算方法。文献[13]不区分地面储能装置的类型，将其视为黑盒，提出了一种求解直流牵引供电系统的双层迭代算法。

以上文献建立了完整的地铁牵引供电系统模型，考虑了再生能量的吸收利用，但是并没有考虑地铁列车和牵引网2 个模块之间的反复耦合关系，没有把车网视为一个整体来仿真，忽略了车网实时耦合的影响。为此，本文提出了基于节点电压模型的地铁供电系统潮流计算方法，为体现网压对列车实际功率发挥的限制作用，推导了不同网压下列车的牵引特性，在此基础上，提出了一种考虑车网耦合的在线潮流计算算法，以计算列车全线路运行过程中的牵引网潮流分布，并基于HLA 仿真架构对算法进行实际线路的仿真研究。

1 地铁供电系统建模

1.1 双边供电系统

我国地铁供电系统主要采用双边供电方式。图1 是以变电所为单位的地铁双边供电系统。与其他供电系统相比，有其自身的特点。首先，系统负荷是移动的，因此求解的网络拓扑结构是时变的；其次，负荷的功率变化速度很快，并且在列车再生制动时，存在能量的反馈；另外，地铁供电系统中交流和直流并存，变电所一次侧为交流潮流计算，二次侧为直流潮流计算。本文中，只考虑直流潮流计算，即潮流计算从图1 中的牵引变电所开始。

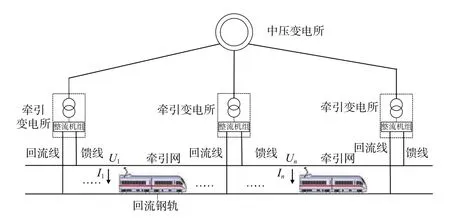
图1 地铁双边供电系统

1.2 模型建立

本文在建立地铁牵引网模型时，忽略次要因素的影响，做出以下基本假设。

1)不考虑交流侧电压的影响。假设交流侧容量无限大，且电压恒定。

2)牵引网和钢轨电阻是均匀的，可以使用集中参数描述。

3)在同一仿真步长内，不考虑牵引网电压变化对列车运行的影响。

4)假设列车在供电仿真步长内为恒功节点。

根据以上假设，构建直流牵引网络的物理模型，如图2 所示。

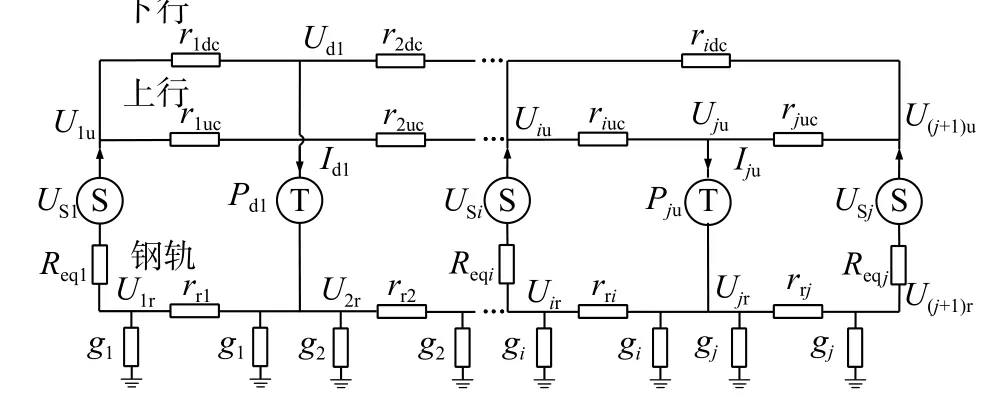
图2 地铁牵引网等效电路模型

直流牵引供电系统潮流计算主要和机车数量、机车位置、机车功率和牵引所直流侧电压有关。图2 中：Pju为机车吸收/反馈的功率；Uju为机车取流处网压；Iju为机车取流；riuc为第i段等效牵引网电阻；Uiu为第i个牵引所出口电压。另外，由文献[14]可知，直流牵引变电所内部可等效为电压源Usi串联电阻Reqi。按照均匀传输线理论，可将钢轨等效为π 模型，rri为第i段等效钢轨电阻，gi为第i段钢轨泄漏电阻。

1.3 模型求解

根据地铁牵引网物理模型生成牵引网的导纳矩阵。具体步骤如下。

1)扫描整个牵引供电网络的拓扑结构，如图3所示，获取每个列车在线路上的位置。

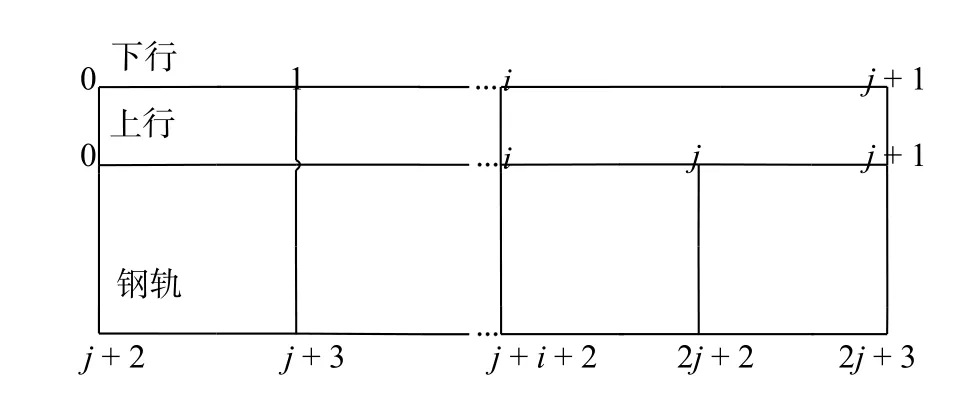
图3 地铁牵引网拓扑结构

2)对变电所和列车的位置进行排序。网络节点的编号顺序依次为变电所馈电节点、变电所回流节点、列车取流节点、列车回流节点，并按照先上行后下行列车的顺序处理，如图3 所示。

3)结合列车位置和牵引网导线基本参数等，解算出牵引网中每段线路的导纳，最后采用支路添加法[9]生成网络的节点导纳矩阵和节点注入电流，具体程序流程如图4 所示。现分别对牵引网中4 类不同节点进行分析。

变电所馈电节点的节点电压方程为

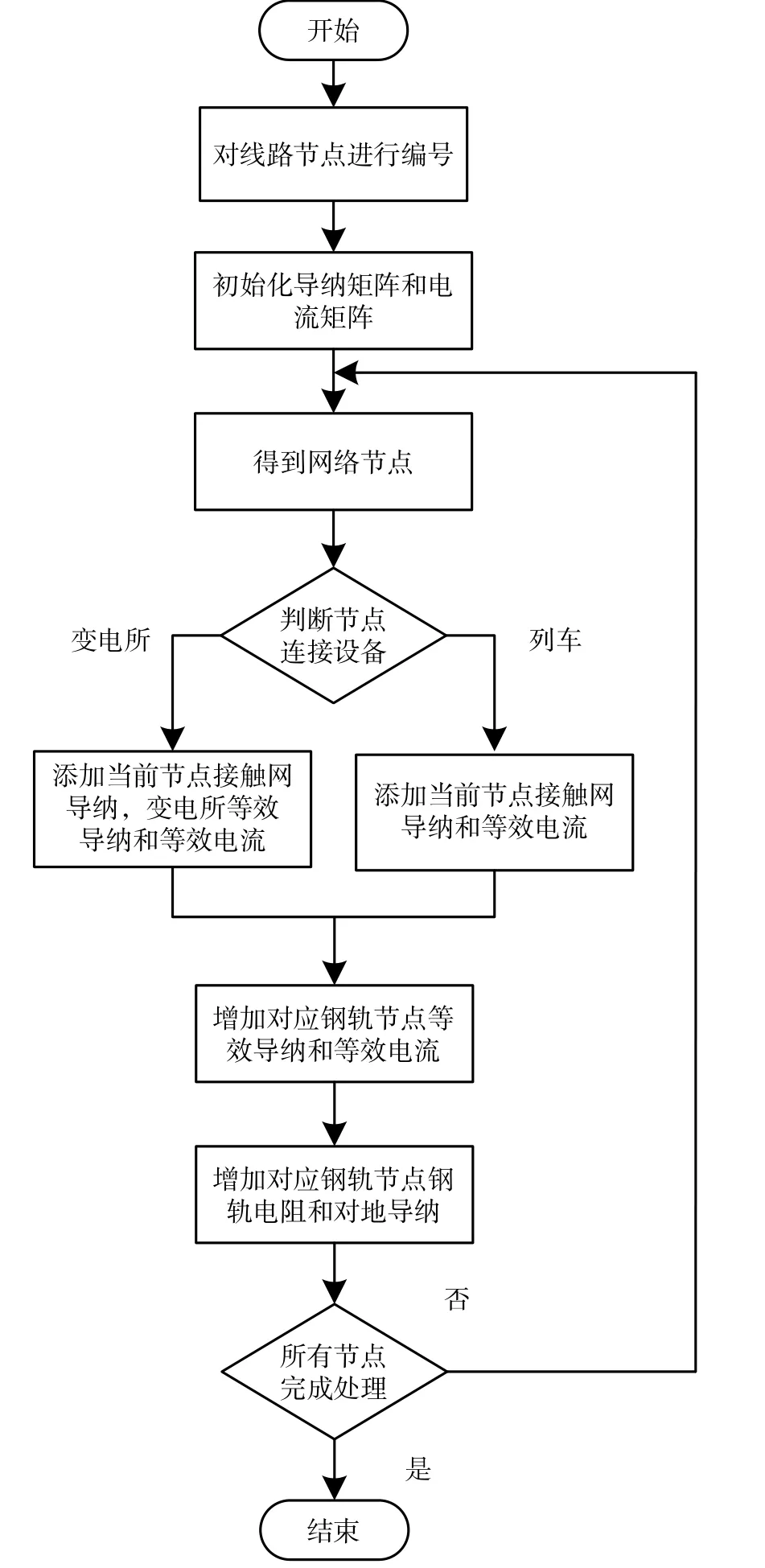
图4 牵引网节点导纳矩阵和节点注入电流矩阵生成流程图

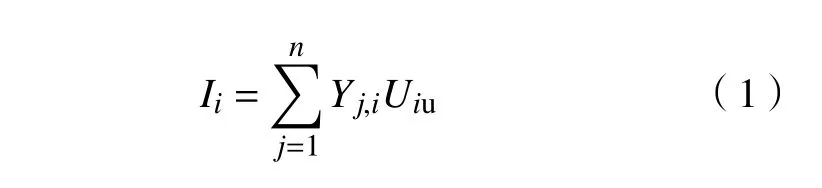
变电所回流节点的节点电压方程为

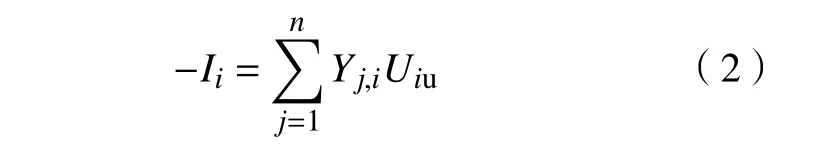
由于列车模型为恒功源，因此可以列出列车节点功率平衡方程。

列车取流节点为

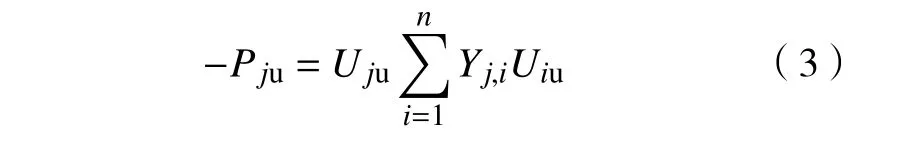
列车回流节点为

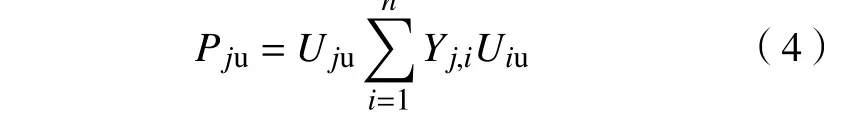
1.4 整流机组等效外特性曲线

城市轨道交通中牵引变电所内整流机组一般采用轴向分裂式三绕组变压器。该变压器在同一铁心柱上装2 个一次绕组和2 个二次绕组，一、二次的2 个绕组沿轴向上下排列，一般一次2 绕组并联，二次2 绕组分裂并且可以分别运行[15]。

本文中，牵引变电所采用12 脉波整流机组。根据文献[16]可得12 脉波整流电路耦合系数为时的稳态电压调整特性为

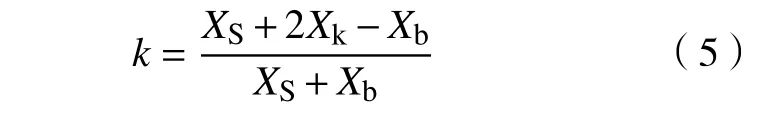
式中：XS为变电所交流电源系统阻抗；Xb为变压器半穿越阻抗；Xk为变压器穿越阻抗。由式（5）可得变压器的耦合系数k=0.35。

在变压器耦合系数k=0.35 时，文献[16]给出了整流机组稳态电压调整特性曲线的计算公式，如式（6）—（11）所示。

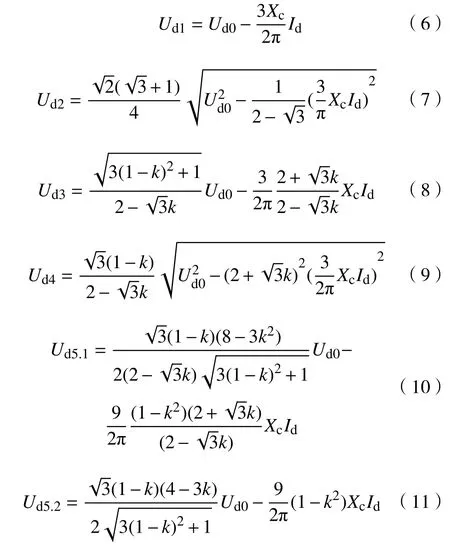
式（6）—（11）中：Ud0为整流机组理想空载直流电压；Xc为变压器换向电抗；Id为变电所馈线电流。整流机组外特性曲线如图5 所示。

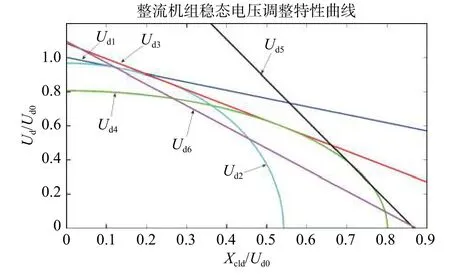
图5 整流机组稳态电压调整特性曲线

图5 中，分别将Ud1和Ud2，Ud2和Ud3，Ud3和Ud4，Ud4和Ud5，Ud5和Ud6的交点连接起来，可得整流机组等效外特性曲线，如图6 所示。

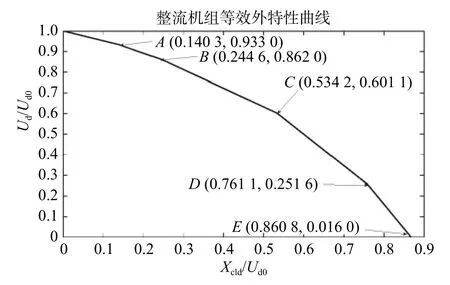
图6 整流机组等效外特性曲线

由图6 可以计算出变电所输出电流在不同范围内，牵引变电所的等效电压和内阻，如表1 所示。

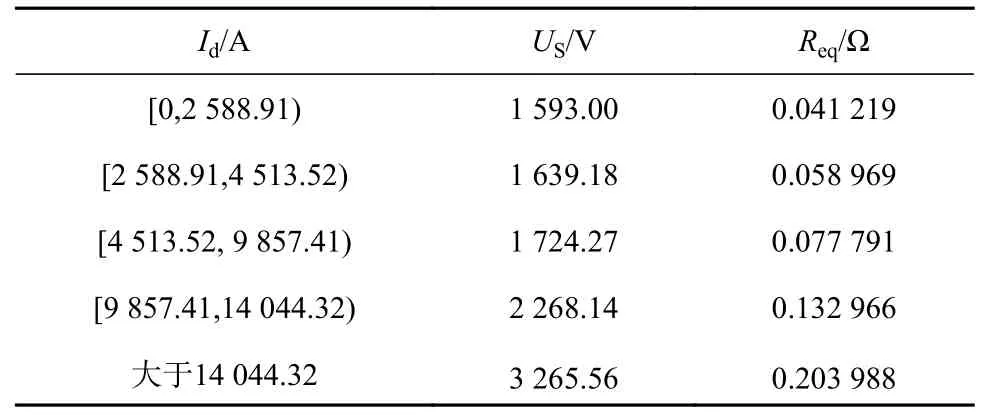
表1 不同负荷等级下变电所等效电压和内阻

1.5 直流牵引网潮流计算

考虑到地铁供电系统的特殊性，本文采用改进线性潮流法[15-16]计算牵引变电所输出功率P1，P2，···,Pn。具体计算步骤如下。

1）牵引变电所输出直流功率计算如式（12）所示。将地铁列车等效为恒功率源模型，每次迭代利用式（13）的注入电流进行计算；采用节点电压法求解潮流方程，如式（14）。

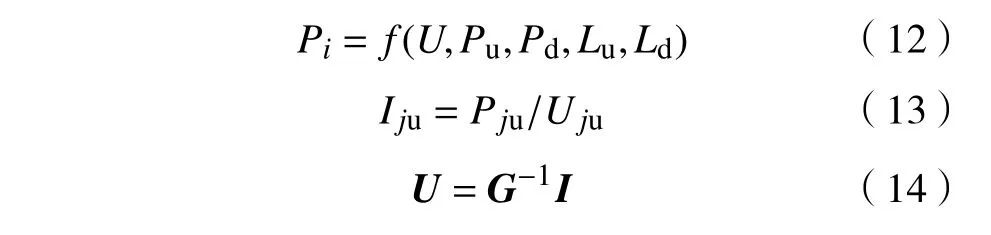
式（12）中：U={Usn,n=1,2,···,i,j,n}；Pu={Pun,n=1,2,···,i,j,n}；Pd={Pdn,n=1,2,···,i,j,n}；Lu={Lun,n=1,2,···,i,j,n}；Ld={Ldn,n=1,2,···,i,j,n}。式（14）中：U、G、I分别表示地铁牵引变电所处电压、导纳、电流矩阵。

2）设定各节点电压初始值，其中机车两端电压初始值U(j0u)=1.5 kV，U=[US1,US2,···,USn]可通过整流机组的外特性曲线获得。

3）将代入式（12）求出各机车等效注入电流初值。

4）利用Gause-Seidel 法得到第k次迭代后的各节点电压，k为迭代次数。迭代公式为

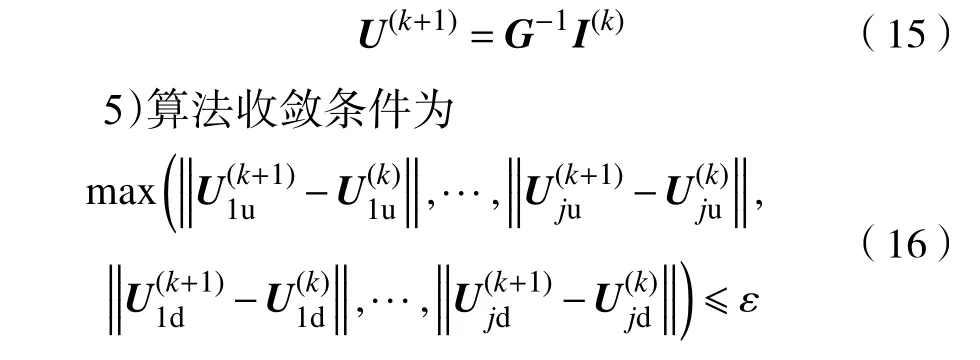
如果式（16）不收敛，则返回步骤1）；若收敛，则进入下一步计算。

整个算法流程采用双层循环结构：外层循环对牵引变电所工作区间进行调整，即调整Vsi和电阻Reqi的值；内层循环进行列车电压的迭代计算。算法流程图如图7 所示。

2 网侧电压对地铁列车实际发挥牵引力的影响分析

在地铁列车运行过程中，当列车网侧电压发生改变时，网侧电流也会随之改变。网侧电压和电流的改变会影响电机负载输出的牵引力，因此列车的牵引特性也应进行调整。

根据能量守恒定律

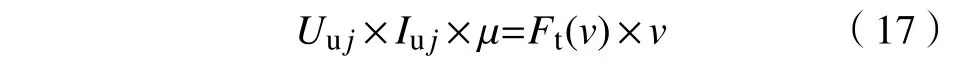
式中： μ为能量转换效率；Uuj为上行第j列车网侧电压；Iuj为上行第j列车网侧电流；Ft(v)为列车速度为v时的列车牵引力。列车牵引特性与网侧电流关系如图8 所示。

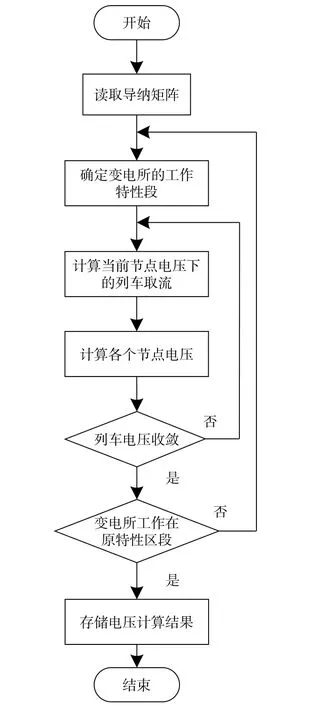
图7 牵引网电压求解过程

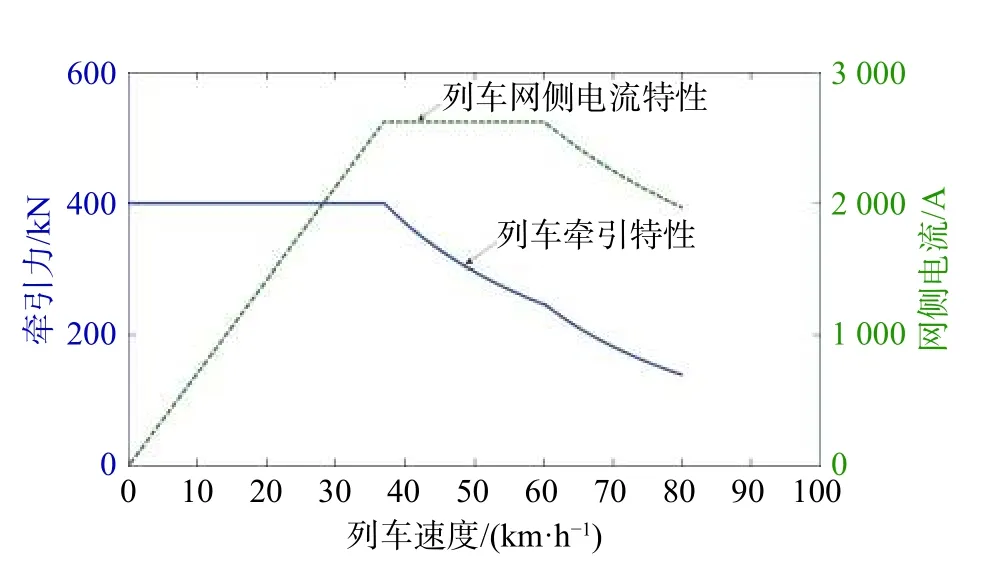
图8 列车牵引特性与网侧电流的关系

从图8 可知，在恒转矩阶段，网侧电流线性上升。当电流恒定时，牵引特性进入恒功阶段，当车速为60 km/h 时，牵引特性进入降功阶段，电流相应下降。由图8 和式（17）可进一步得出列车网压波动时的牵引特性与网侧电流关系，推导过程如下。

设列车分别运行在1.2 kV 和1.5 kV 电压等级下，且功率恒定。

当列车运行在1.2 kV 电压等级下，

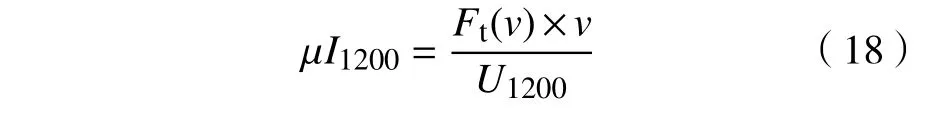
当列车运行在1.5 kV 电压等级下，

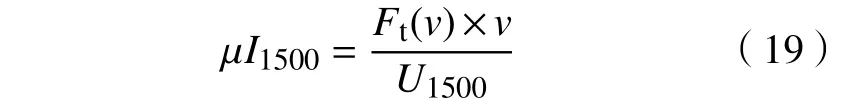
由式（18）和式（19）可得，

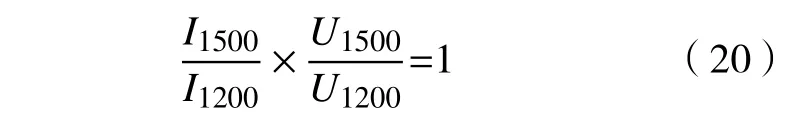
对式（20）右边进行恒等变化，得

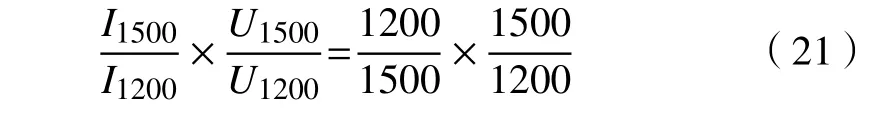
式（21）中，1200 和1500 分别对应1.2 kV、1.5 kV 电压等级，比较等式左右两边，网侧电压关系为

同理，网侧电流为

由此可得列车牵引特性与网侧电流的关系，如图9 所示。

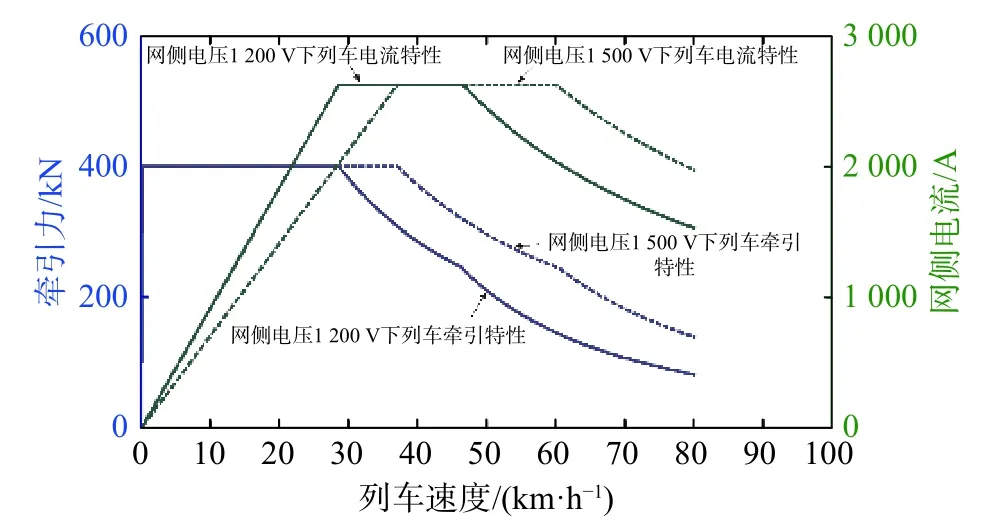
图9 列车牵引特性与网侧电流的关系

图9 中，在网侧电压为1.2 kV 情况下，为了保证启动加速度及恒转矩区间力矩不发生变化，根据式（17）可知，在网压降低的情况下，列车运行速度不变，为了输出额定电压下同样大小的牵引力，必须产生更大的网侧电流。另外，当网侧电压较小时，网侧电流的特性曲线线性上升速度更快，当电流上升到恒电流区时，对应的牵引特性曲线会进入恒功区。恒转矩和恒功区都相应收缩了U1200/U1500。此时，列车启动加速度可以保证，但是线性加速区比较短，所以列车启动平均加速度会略低于额定网压下的情况。

在额定载荷等级下，各电压等级下的牵引特性如图10 所示。

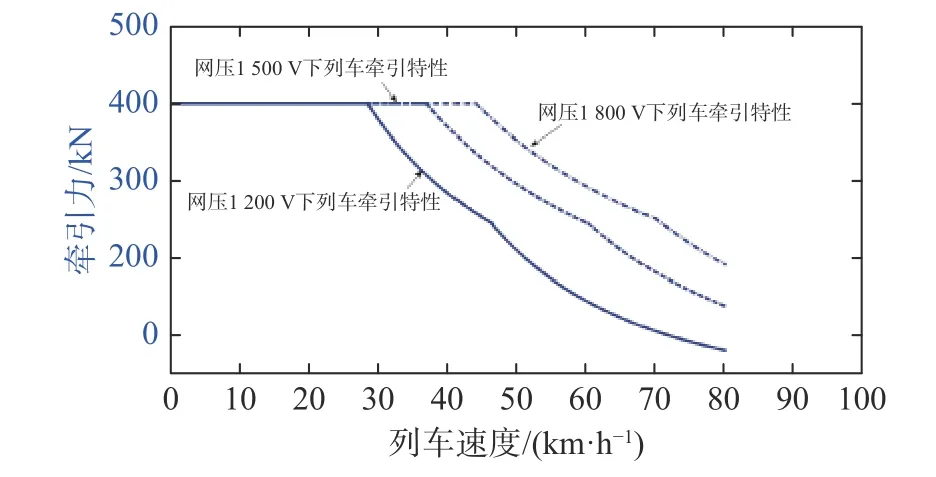
图10 额定载荷下不同电压等级时的牵引特性

若网侧电压升高到1.8 kV，网侧电流升高会变得更慢，网侧电流需要更多的时间才能上升到恒电流区。由于网侧电流的线性增长区域与牵引特性的恒转矩区域是对应的，所以此时牵引特性的恒转矩区会相应延长。通过计算可以得出恒功率转折点对应的速度变为原来的U1800/U1500，牵引特性沿横轴拉伸U1800/U1500倍。在1.8 kV 的网侧电压下列车的加速性能会略高于额定电压的加速性能。

综上所述，在不同网侧电压下，列车所呈现出的牵引特性是不一样的。在多列车运行与供电系统联合仿真过程中，网侧电压会不断变化。为了描述不同网压对列车运行的影响，建立列车三维牵引特性模型。常规的牵引特性图，以X轴描述列车速度，以Y轴描述牵引力。在此基础上，添加Z轴，以描述网侧电压。得到的不同电压等级下的牵引特性，如图11 所示。

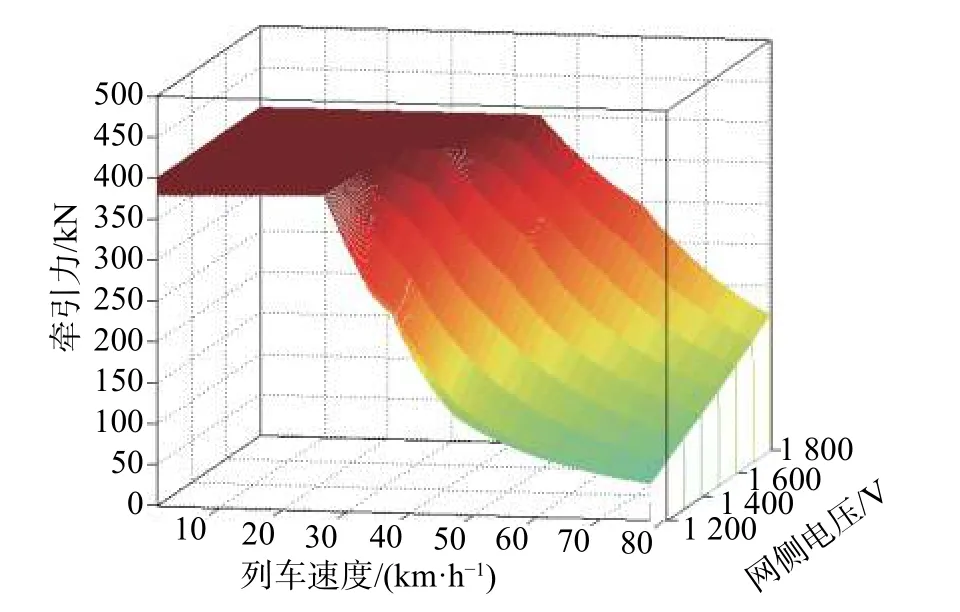
图11 列车三维牵引特性

以上分析表明，在低网压或高网压情况下，网压影响列车牵引力实际发挥，因此在牵引计算的同时须同步开展牵引网的潮流解算，根据网压判断列车的实际发挥功率，并在此基础上对列车运行过程进行求解。

3 基于HLA 架构的车网耦合仿真平台

3.1 HLA/pRTI

HLA（high level architecture）是美国国防部推出的一种分布交互仿真标准，也是一个开放的、支持面向对象的体系结构。RTI（run time infrastructure）是遵循HLA 标准的运行支撑框架软件，在仿真执行过程中负责联邦成员[17]间的信息交互。

本文采用pRTI 框架搭建仿真平台，将牵引供电仿真计算模块和车载控制器模块分别作为联邦成员加入联邦[17]进行仿真，各个联邦成员通过定义对象类和交互类收发数据，其数据更新机制如图12 所示。

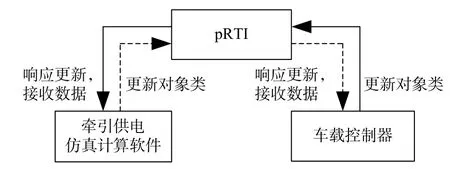
图12 pRTI 数据更新机制

3.2 车网耦合下的供电系统潮流解算

车网耦合下供电系统潮流解算平台如图13 所示。

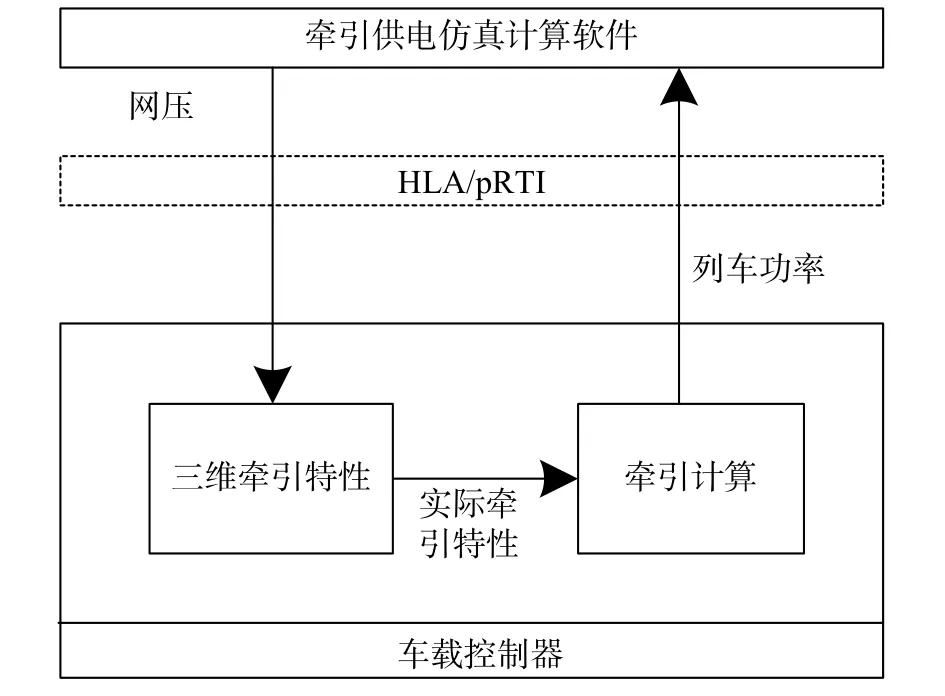
图13 车网耦合下供电系统潮流解算平台

进行车网耦合工况下牵引网潮流计算时，先由车载控制器牵引计算模块确定列车运行需求功率，通过pRTI 传递给牵引供电仿真计算软件，然后供电计算软件根据当前功率和初始网压U0进行迭代后得到实际网压，该网压再通过pRTI 传递给车载控制器的三维牵引特性模块，由该模块计算获得当前网压下的列车牵引特性曲线，最后将该曲线传递给牵引计算模块。耦合工况下牵引网潮流计算过程如图14 所示。

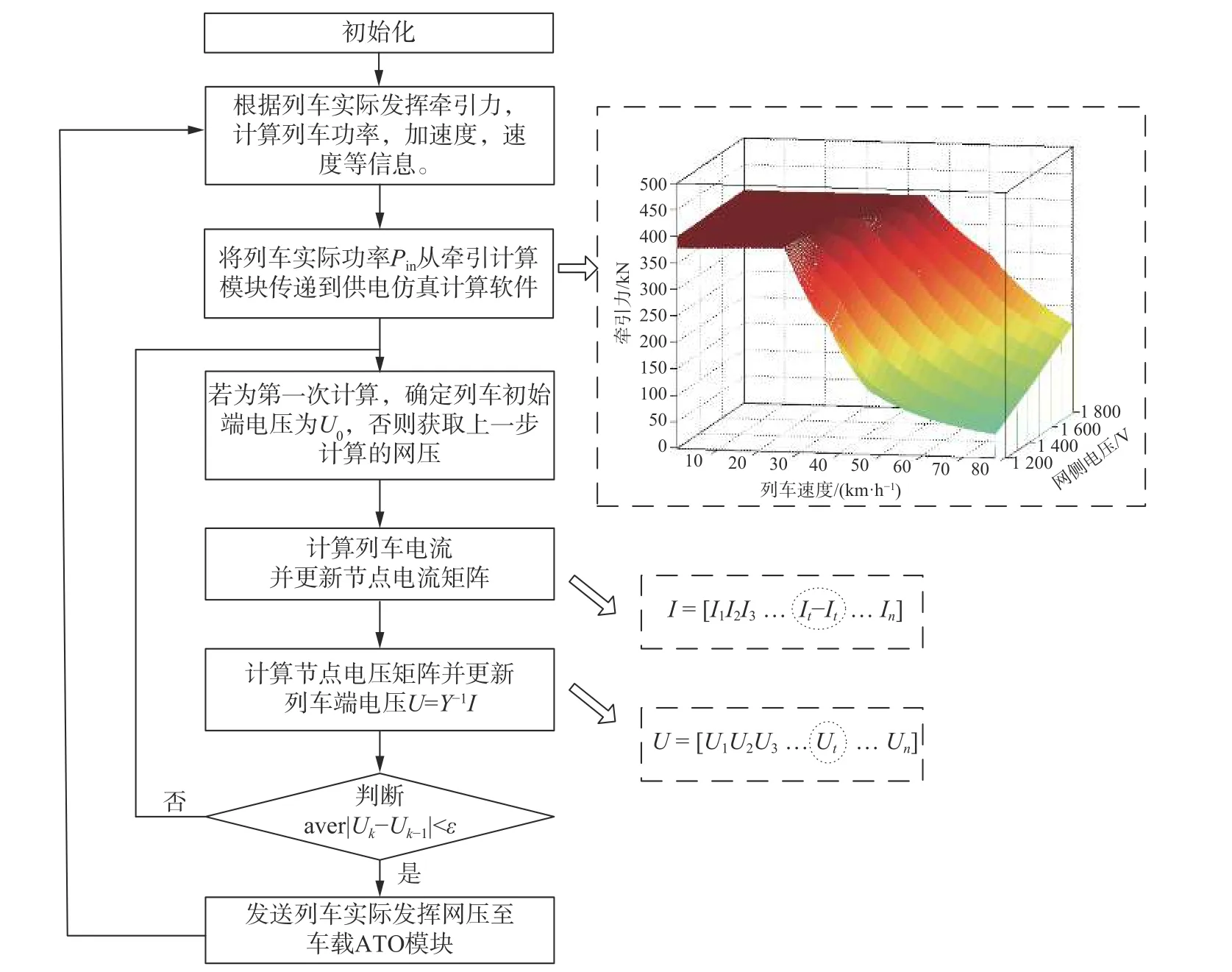
图14 耦合迭代潮流计算流程图

4 仿真算例与分析

本文选取深圳地铁一号线首期工程线路（罗湖站—侨城东站）进行仿真验证。

4.1 仿真条件

列车编组为4 动2 拖，主电路采用VVVF 控制，最高运行时速为80 km/h，以最大能力运行。列车载荷质量为342.6 t，运行基本阻力Fr=9.19+0.001 334v2(kN)，v取km/h。

牵引变电所采用2 台相同参数的12 脉波整流机组并联运行，整流机组参数如表2 所示。

表2 整流机组基本参数

4.2 仿真分析

4.2.1 极大值原理

上下行列车在同一时刻相对发车，以上行第一列车为观测对象，基于极大值原理[18]，本文分别仿真罗湖站—国贸站考虑车网耦合（考虑网压对列车牵引性能发挥的影响）和不考虑车网耦合（不考虑网压对列车牵引性能发挥的影响）2 种情况。列车运行的速度-距离曲线和牵引力-距离曲线如图15所示。

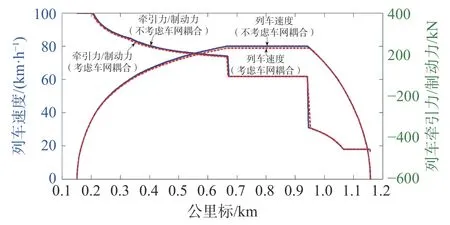
图15 单区间速度-距离和牵引力-距离对比图

在列车起动阶段，列车向网侧取流导致电压降低，由三维牵引特性可知，恒转矩区会缩短，此时的加速性能略低于理想额定情况下的加速性能。在图16 的网压-距离曲线中，在恒功阶段，不考虑车网耦合时的网压略低于考虑车网耦合时的网压。

从图16、17 中可知，考虑车网耦合时，在起动阶段，列车牵引力由于受到网压的制约而无法完全发挥，列车实际发挥功率也因此受到影响，故考虑车网耦合情况下列车在牵引工况时的网压高于不考虑车网耦合情况下列车处于牵引工况时的网压，机车取流则相反。

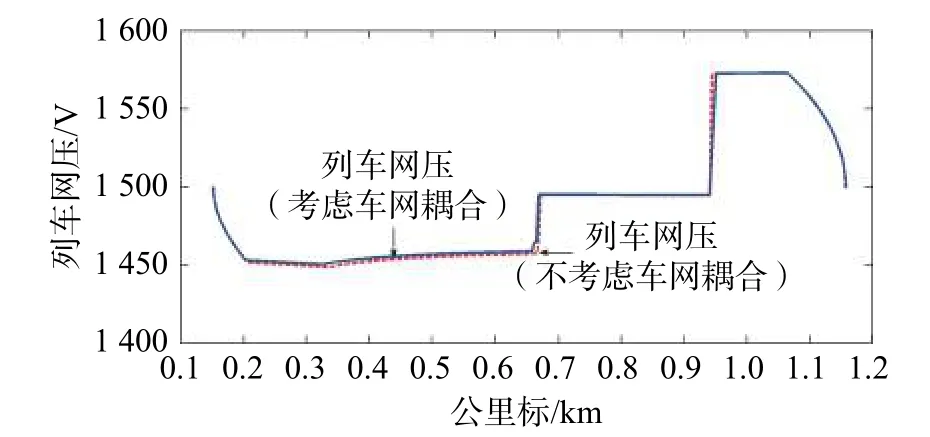
图16 列车网压-距离对比图

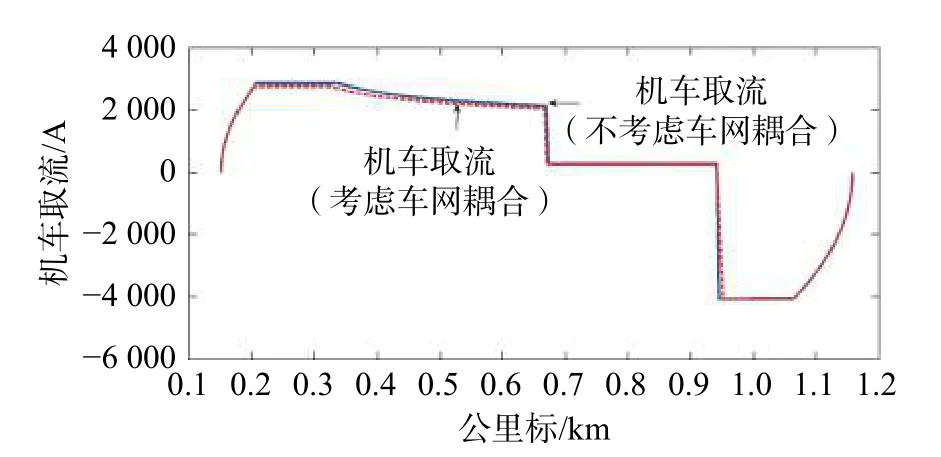
图17 列车网流-距离对比图

图18 示出当变电所容量降低为原来的1/2时，上行第一列车的网压变化曲线。由图可知，除恒速阶段外，列车在全力牵引和制动阶段时（再生制动），牵引变电所的容量对列车运行网压有显著影响。

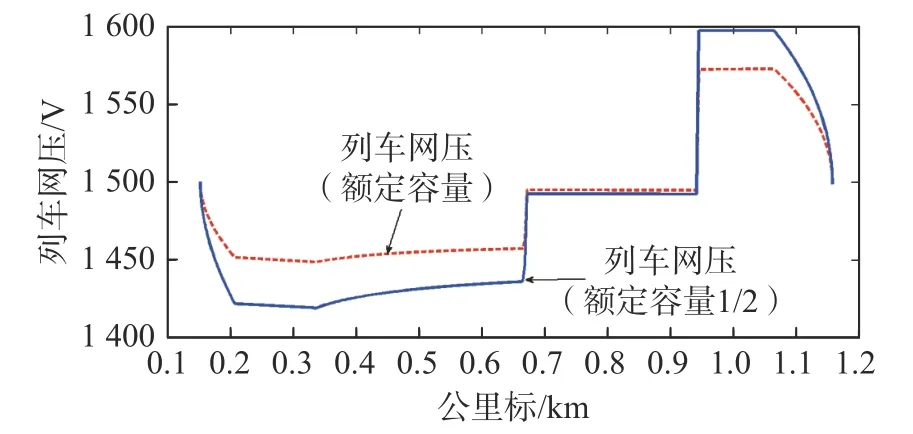
图18 不同变电所容量下列车运行网压

图19 和图20 分别示出在不同发车间隔下，上行第一列车的网压变化情况。

由图19 可知，当发车间隔为120 s 时，线路上的2 辆列车同时制动，会导致网压较大幅度的上升。由图20 可知，当发车间隔为100 s 时，前车制动时，后车恰好在牵引，可抵消由于列车再生制动引起的网压上升。

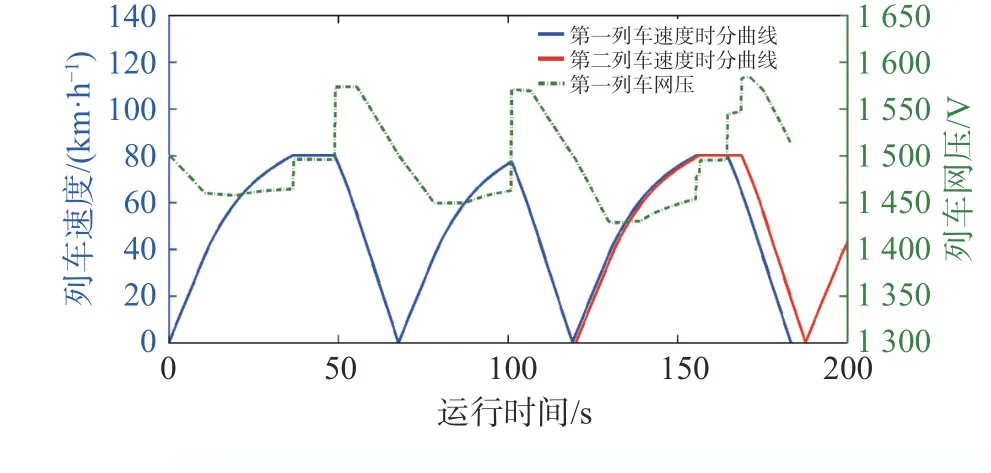
图19 列车网压变化（120 s 发车间隔）

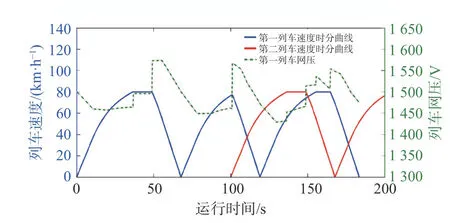
图20 列车网压变化（100 s 发车间隔）

图21 示出变电所容量为额定值（100 MVA）与非额定值（50 MVA）时的潮流迭代过程，迭代收敛误差为0.1 V。

图21 迭代误差曲线图

由图21 分析可知，在变电所容量不同的情况下，本文所采用的潮流算法均能达到很好的收敛效果。因为直流潮流计算采用连续线性潮流法求解，迭代过程中节点导纳矩阵保持不变，且节点导纳矩阵为对角占优矩阵，因此迭代过程必收敛。

4.2.2 遗传算法

本文基于自适应遗传算法[19]，进一步仿真了100 s 和120 s 发车间隔条件下列车运行网压的变化，其结果如图22 和图23 所示，其网压分布规律与基于极大值原理得到的结果类似。不同之处在于，由于采用了遗传算法，在120 s 和100 s 发车间隔条件下，列车由恒速转入制动之间插入了一段惰行，所以图22 所示第二列车的峰值网压下降6 V，图23 所示第2 列车在制动停车阶段的峰值网压下降3 V。

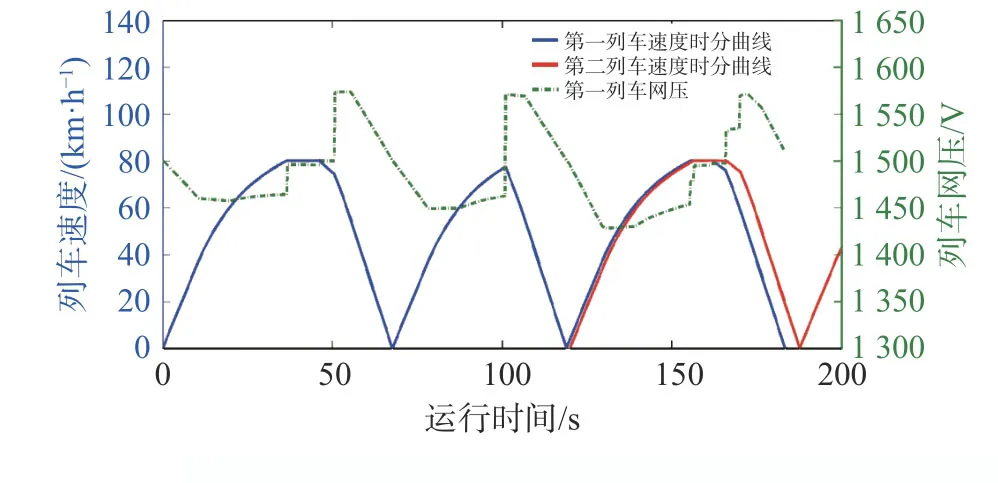
图22 列车网压变化（120 s 发车间隔）

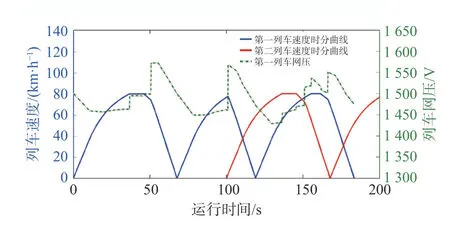
图23 列车网压变化（100 s 发车间隔）

5 结论

本文提出了一种地铁供电系统车网耦合下的潮流计算方法，可计算当列车牵引力发挥受网压限制时全线运行过程中的牵引网潮流分布，并基于HLA 仿真架构建立了列车运行与供电系统耦合仿真平台。通过对基于极大值原理和遗传算法的仿真算例进行分析，得到如下结论。

1）当列车轮周牵引力因网压波动受限时，列车运行速度曲线将受到影响，在网压波动较大时尤为明显。因此，当变电所容量过小、列车功率过大或多列车运行情况下，研究列车优化操纵策略须考虑网压对列车运行的影响。

2）当列车轮周牵引力因网压波动受限时，考虑车网耦合进行潮流计算得到的网压比未考虑车网耦合进行潮流计算得到的网压高，反映了车网耦合下列车运行网压分布。

3）多列车运行时，通过合理设置发车时间间隔和列车间的运行工况组合，可有效地抑制网压波动，使列车牵引/制动性能得到正常发挥。

4）耦合模型为进一步研究供电系统容量约束下的列车群控制策略具有重要意义。