整合资源重变式，深化认知建模型

李丽萍

几何图形是现实物体的抽象。教学中教师应该将资源进行适当的整合，借助变式还原图形的本质。练习的设计除基本的技能训练外，还不能忽视对知识本质和解决问题方法的探寻。形成思维方式比单纯地掌握公式更重要，建立模型比会用公式计算更重要。

一、抓住原型，感受知识联系

有一道习题：如图1，圆环的面积是628 cm2，阴影部分的面积是（  ）cm2。这道习题得分率仅为31.5%，可以引发我们的思考。

此题的原型（如图2所示），已知圆的面积是21.98平方厘米，求正方形的面积是多少平方厘米？（已知单个圆的面积求正方形的面积）。如果认为此题需要结合逆向思维，可先解决“已知正方形的面积求圆的面积”。

这类题型学生最大的障碍在于怎么求出圆的半径，但越是想要求出半径，越无从下手。如何突破这个思维定势？回到图2，仔细观察，正方形的边长等于圆的半径r，正方形的面积就等于r2。看来，求圆（正方形）的面积直接需要的条件是r2，而非r。把r2看作一个整体代入S圆=πr2。反过来，已知圆的面积求正方形的面积（r2）：r2=S圓÷π。

回到圆环这道题，同样的道理：图中外圆的半径等于大正方形的边长，内圆的半径等于小正方形的边长，阴影部分的面积可以表示为R2-r2，把R2-r2看作一个整体代入S环=π×（R2-r2）中求，得到S阴=S环÷π。

把“圆环”降为“圆”，不是简单“两个”变“一个”，这里体现着知识之间的内在联系，在变与不变的思考辨析中，学生学会在变式中找到原型，在原型中发现解决这类题型的方法。

二、举一反三，巩固解题方法

从一题出发让学生学会举一反三，巧用整体代入法解决类似的问题。就如，教师可以提问：“这个正方形能不能换成其他图形，这个方法还适用吗？”在教师的引导下，学生想到可以用等腰三角形替换原来的正方形，此时只要抓住这个等腰三角形面积是原来正方形的，再用整体代入法来解决就简单多了。

教师还可以出示变式题组，继续引导学生发散思维。

（1）图3，正方形的面积是12平方厘米，求阴影部分的面积（π=3.14，下同）。解题思路：S正=4r2=12→r2=3→S阴=3π=9.42 （cm2）。

（2）图4，大正方形的面积是20平方厘米，求阴影部分的面积。解题思路：S正=4r2=20→r2=5→S阴=20-5π=4.3（ cm2）。

（3）图5，已知阴影部分的面积是16平方厘米，求圆环的面积。解题思路：S阴=2R-2r2=16→R2-r2=8→S环=8π=25.12  （cm2）。

有同一维度的拔高，也有多个维度的提升，由浅入深，由表及里，让学生在举一反三中，发现其中的规律，达到突破难点的目的，培养学生的观察、分析能力。

三、还原本质，促进认知深化

（一）分析错因，返“璞”归真

在学生的练习中，我们不难发现这样的错误：S环=π×（R-r）2。教师需要帮助学生厘清形式相似的π×（R2-r2）和π×（R-r）2有什么本质上的不同。

回到生活中常见的箭靶，有9个圆环，虽然每个圆环的环宽一样，但是从里往外，圆环的面积是越来越大。如果S环=π×（R-r）2的话，得到结果都相等，这就产生矛盾，所以两个数的平方差和这两个数差的平方是不同的。通过对错因的分析，加深学生对圆环面积公式的理解，也使其明白在射箭比赛中为什么射中不同环的得分不一样。

另外，部分学生还理不清外圆的半径、内圆的半径、环宽三者关系。如：苏颂公园里有一个直径6米的圆形喷水池，要在它的周围铺上1米宽的小路。求小路的面积是多少平方米？此题学生往往会这样做：内圆的面积，3.14×（6÷2）2=28.26（m2）;外圆的直径，6+1=7（m）;外圆的面积，3.14×（7÷2）2=38.465（m2）;圆环的面积：38.465-28.26=10.205（m2）。

学生的解题思路是没有错，错在求外圆的直径时忘了加另外一端的小路的宽度。现实中的“型”本质在于图中的“形”，如果学生在做题时能够借助“形”来辅助理解外圆的半径=内圆的半径+环宽、外圆的直径=内圆的直径+2条环宽，相信学生在碰到类似题时便不会再有困惑。

（二）借助史料，还原本质

学生受知识正迁移的影响，认为圆环的面积只能是外圆的面积减内圆的面积。还能转化成什么？回顾圆的面积推导过程，我们利用“化曲为直”的方法，把圆的面积转化为等面积的近似长方形，想象一下：圆环是不是也可以这样拉直？在北师大版教材的“数学万花筒”中有这样的介绍，可以把一个由草绳编织成的圆形茶杯垫片，沿着半径剪开后可拼成一个等腰三角形。圆环可以看作两个同心圆，它们都转化为三角形重叠在一起，相差部分就是梯形，上底是2πr（内圆的周长），下底是2πR（外圆的周长），高是R-r（半径之差），梯形的面积就是圆环的面积。这个方法在我国古代数学专著《九章算术》中有记载：今有环田，中周九十二步，外周一百二十二步，径五步。问田几何。答曰：二亩五十五步。术曰：并中外周而半之，以径乘之为积步。

四、拓展延伸，建立数学模型

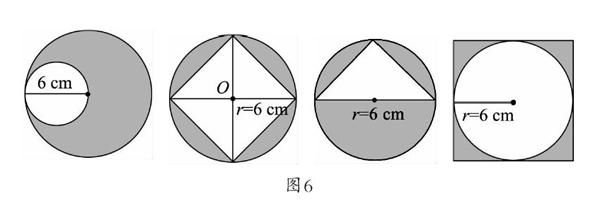
在学生理解掌握了圆环的概念、圆环面积的计算之后，我们很有必要针对这类图形建立数学模型，让学生由感性认识提升到方法的概括。于是笔者设计这样一组题型（如图6）。学生通过计算每个图形阴影部分面积后，归纳总结出计算方法的相同之处。这组题都不是圆环的面积，但用的方法跟求圆环的面积思路（大的面积-小的面积）是一样的，从而拓展了计算组合图形面积的一般方法，建立数学模型。

通过对一道习题的研究与思考，发现学生需要一个呈现知识及关系的平台，来沟通知识间的内在联系和深化认知;教师教学需要精选范例，关注变式，整合习题资源，还原知识本质，有效落实教学目标，用“做”悟“学”，立足思维起点并向深处迈进。

（作者单位：福建省厦门市同安区新城小学 责任编辑：王彬）