VMD的AR模型和关联维数在齿轮故障特征提取中的应用*
2021-01-06周小龙张耀娟马风雷
周小龙 张耀娟 王 尧 马风雷
(①北华大学机械工程学院,吉林 吉林 132021;②长春工业大学机电工程学院,吉林 长春 130012)
齿轮传动具有效率高、装配方便、易于润滑等优点,在旋转机械设备中应用广泛。由于工作环境恶劣,齿轮是易损元件,齿轮故障是导致机械设备失效的主要原因[1]。因此,对于齿轮故障特征的提取及诊断方法的研究具有十分重要的意义[2]。
当齿轮出现故障时,其振动信号常表现出非线性特征[3]。分形理论中的关联维数[4]可有效反映该类信号的不规则性和复杂程度[5]。然而,工程实际测得的机械振动信号中含有大量环境噪声,关联维数对信号的信噪比十分敏感,若直接计算原始信号的关联维数,结果可靠性低,难以实现工作状态和故障类型的识别;另外,为全面监测设备的运行状态,信号采集过程中的采样频率和时长不易过小,由此造成采集到的数据量庞大,若直接对其关联维数进行估计,计算量巨大。所以在计算关联维数前有必要对原始信号进行降维处理,以提升关联维数的计算效率,提高故障特征提取的效率。
经验模态分解(EMD)是近年来由Huang[6]等提出的一种处理非线性信号的有效方法,但EMD在分解过程中存在模态混叠问题,集合经验模态分解[7](EEMD)是目前解决该问题最常用的方法,但受限于总体平均次数,EEMD向信号内添加的白噪声无法完全消除,不具有完备性。变分模态分解[8](VMD)是非递归式信号分解方法,可将复杂信号分解成若干个具有调幅-调频特性的固有模态函数(IMF)分量,具有良好的噪声鲁棒性,可更为有效地抑制模态混叠问题的产生。
基于上述分析,笔者将VMD的自回归(AR)模型和关联维相结合,应用于齿轮故障特征提取。对实测齿轮振动信号的分析结果表明,所提方法可有效应用于齿轮故障诊断。
1 基本理论
1.1 基于VMD的AR模型
对于齿轮振动信号x(t),VMD算法首先对其建立变分约束模型:
(1)
式中:∂t为对函数求时间t的偏导数;δ(t)为单位脉冲函数;K为模态分解个数;uk(t)为第k个模态分量;ωk为uk(t)的中心频率。
引入增广拉格朗日函数ζ,将约束问题转化为非约束问题:
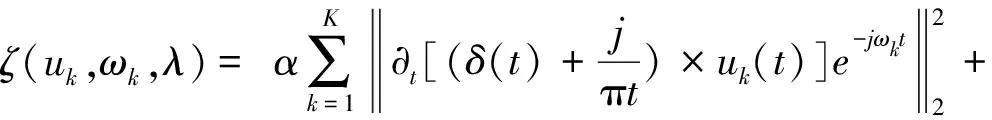
(2)
式中:α为二次惩罚因子;<>表示向量内积。
采用交替方向乘子法求解式(2)变分约束模型的最优解。求得的模态分量uk及中心频率ωk分别为
(3)
(4)
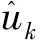
给定判定精度e>0,若满足迭代约束条件:
(5)
则停止迭代,输出结果;否则继续迭代,直至满足上式为止,最终得到模态分量uk和ωk。
对VMD分解得到的任一IMF分量ui(t)建立AR模型AR(m)[9]:
(6)
1.2 关联维数
关联维数主要用于刻画系统的非线性行为,描述其复杂性。在此采用关联维数计算最常用的G-P算法,其计算步骤如下:
设{φ1,φ2,…,φk}为齿轮振动信号经VMD分解得到的1个IMF分量ui(t)的AR(m)模型参数序列,k= 1,2,3,…,m,相空间重构后的一对相点为

(7)

(8)
则φi和φj间的欧式空间距离rij:
rij=|φi-φj|
(9)
设r为距离阈值,C(r)为距离rij小于r的点对数在所有点对数中的比例:
(10)
式中:N为总相点数;θ(x)为Heaviside函数,即:
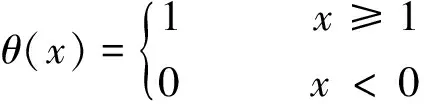
(11)
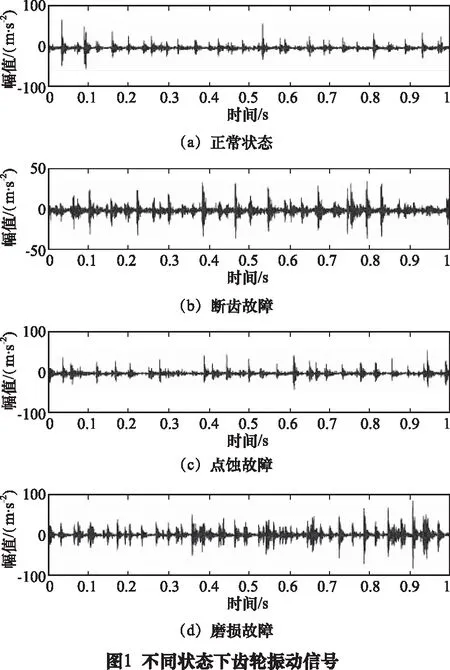
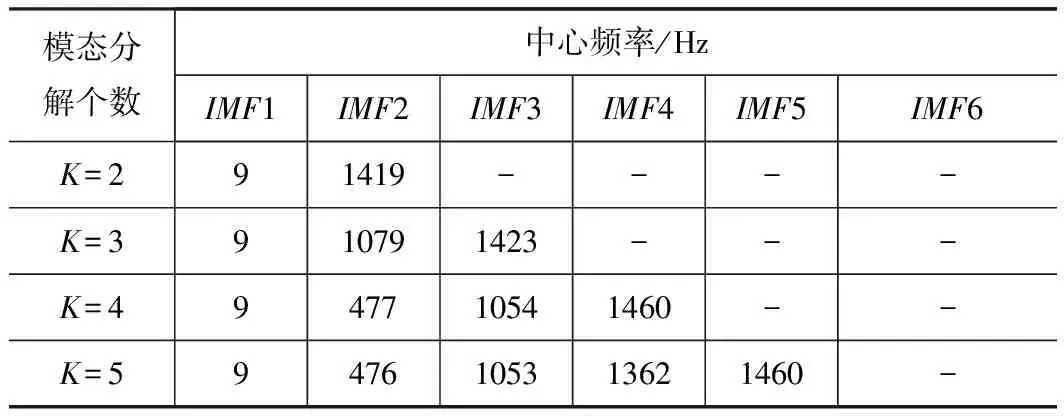
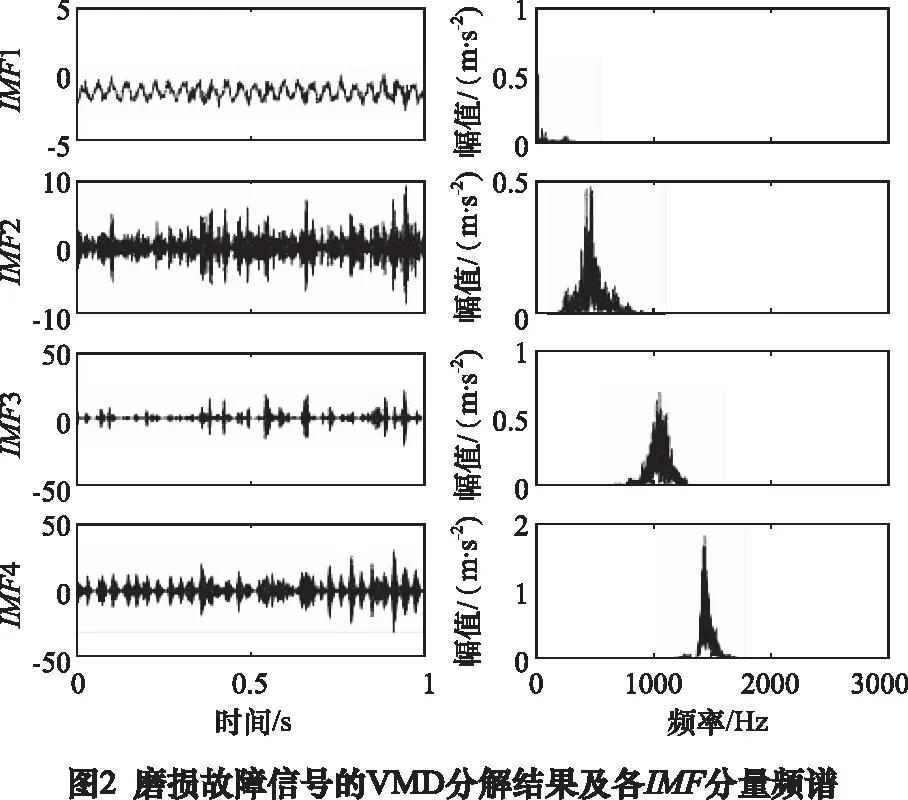
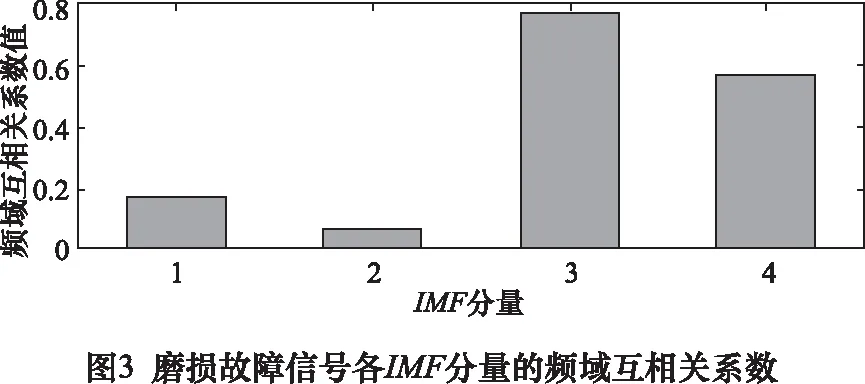
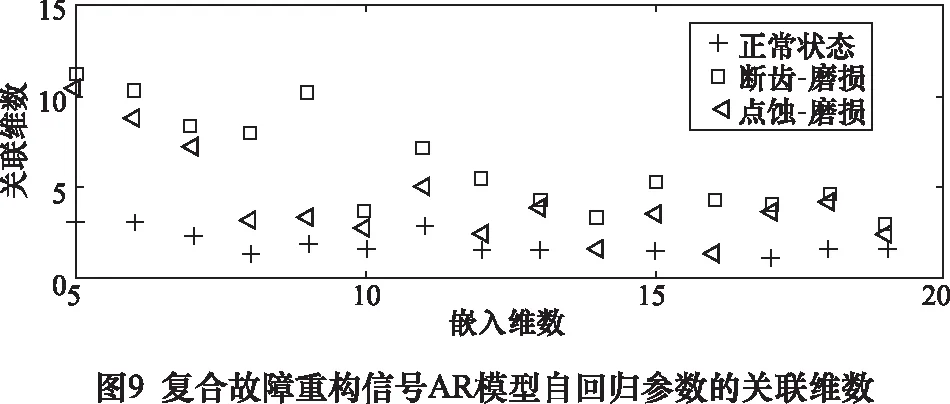
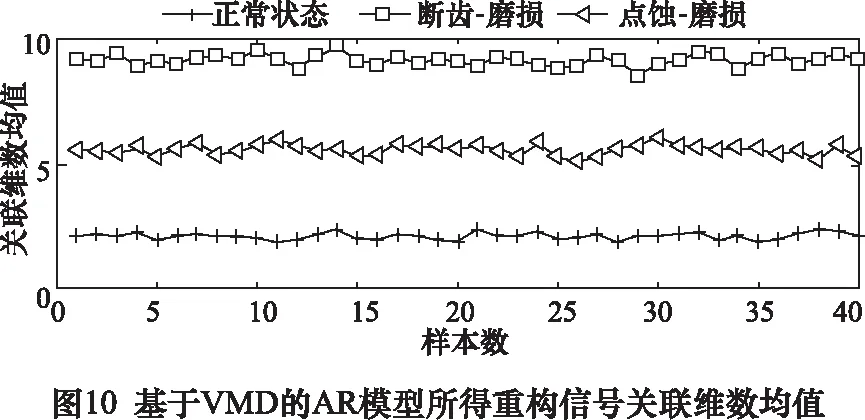
C(r)为关联积分,表示相空间中两点间距rij C(r)∝rD (12) 式中:D为关联维数,可根据下式对其具体求解: (13) 因此,分别以lnr和lnC(r)为横、纵坐标,则lnC(r)-lnr变化曲线的斜率对于逐渐增大的嵌入维数n逐渐收敛于一个值,则该值即为关联维数D。 为验证所提方法的有效性和实用性,在机械故障模拟综合试验台进行齿轮断齿、点蚀和磨损故障的模拟。其中,输出轴和输出轴齿轮为标准直齿轮,齿数分别为75和55,模数为2 mm,磨损故障设置在小齿轮上,断齿和点蚀故障设置在大齿轮上。 试验过程中,电动机转频为50 Hz,输入轴转速为1 500 r/min,加速度传感器型号为KD1001L型,安装在齿轮箱轴承座上。数据采集系统的搭建以ADA16-8/2(LPCI)型采集卡为基础,采样频率5 120 Hz,采样时长5 s,分析时长1 s。不同状态下,随机选取1组采集到的齿轮加速度信号的时域波形如图1所示。 由图1可知,不同状态下齿轮振动时域波形存在相似性,信号中包含较多噪声和背景干扰成分,若对此信号进行关联维数计算,势必会影响计算准确性,降低故障检测精度。 为有效滤除干扰成分的影响,对上述信号进行VMD分解,通过频域互相关准则选取敏感IMF分量用于信号重构,以实现信号的信号去噪与提纯。 由VMD算法可知,模态分解个数K的选取恰当与否将直接影响分解效果。本文以各IMF分量中心频率是否出现相近值法确定K的最佳值。 选取图1d齿轮磨损故障信号,对其进行VMD分解,不同K值下各IMF分量的中心频率如表1所示。 表1 不同K值对应的各IMF分量中心频率 由表1可知,当K=3时,IMF1和IMF2的中心频率数值相差很大,表明出现了欠分解现象;当K= 5时,IMF4和IMF5的中心频率数值十分接近,表明出现了过分解现象。因此,可认为模态分解个数K的最优取值为4。 惩罚参数α决定了分解得到的各IMF分量的带宽,通过对大量齿轮振动信号分解结果的测试并结合文献[8],本文选取α= 2 000。 基于上述分析,磨损故障信号的VMD分解结果和各IMF分量的频谱如图2所示。 由图2可知,VMD分解结果较为合理,各IMF分量的频率集中在其中心频率附近,未出现明显的频率发散现象。 为更好地提取故障特征,需选取分解结果中可有效表征故障信息的模态分量进行信号重构。按式(14)分别计算各IMF分量与原信号间的频域互相关系数[10],结果如图3所示。 (14) 式中:设Gu、Gx分别为信号ui和xi功率谱;fa为分析频率;ui为IMF分量;xi为原齿轮振动信号。 由图3可知,IMF1为表征低频迭代误差分量,IMF2为表征噪声干扰分量,故其频域互相关系数值非常小。因此,将IMF3和IMF4作为敏感模态分量用于信号重构。重构信号的时域波形如图4所示。 由图4可知,重构信号的时域波形内冲击成分得到有效凸显,信号特征明显。按上述步骤,对图1中其余信号进行VMD分解,并计算各IMF分量的频域互相关系数以获取重构信号。 为有效提升关联维数的计算效率和准确性,对经VMD重构的信号建立AR模型,采用最终预测误差(PPE)准则确定模型阶数m,并由时延相图法重构AR模型自回归参数的相空间,计算其关联维数。 不同状态下齿轮重构信号的AR模型自回归参数的关联维数计算结果如图5所示,其中嵌入维数取值范围为5~19。 由图5可知,不同状态下重构信号AR模型自回归参数的关联维数除在个别嵌入维数上数值较接近外,总体区分度较好。由此表明,可将该关联维数作为特征向量对齿轮的故障类型进行诊断。 图6为不同嵌入维数下直接对原始齿轮振动信号计算所得关联维数。图7是原始齿轮振动信号建立AR模型后所得AR模型自回归参数的关联维数。由图6和图7可知,不同状态下齿轮振动信号的关联维数十分接近,难以对其工作状态进行有效区分。究其原因,主要是实际采集到的齿轮振动信号中含有大量环境噪声,关联维数对信噪比敏感,从而影响了其计算结果的准确性;此外,齿轮振动信号的AR模型自回归参数虽然凝聚了其工作状态和运行规律的重要信息,但其本质是线性预测模型,难以实现非线性信号的准确建模。 结合图5计算结果,选取嵌入维数为5、6、9时关联维数均值作为特征值以实现对齿轮工作状态和故障类型的高效识别。 图8给出了输入轴转速1 500 r/min,分析时长1 s条件下,本文方法处理所得每种状态下40个样本的关联维数均值。由图8可知,在选定嵌入维数上的关联维数均值可有效区分齿轮工作状态,实现故障类型的诊断。由此可知,齿轮振动信号经VMD重构后,信号内的背景噪声得到有效滤除,对重构信号建立AR模型,实现了非线性齿轮振动信号的线性化,AR模型自回归参数保留了不同状态信号间的特征差异,并有效剔除了信号中的随机干扰,保证了关联维数的计算准确性,可作为评判齿轮状态的依据。 为检验所提方法的适用性,使用同样的故障齿轮设置断齿-磨损和点蚀-磨损复合故障。 选取输入轴转速1 500 r/min,分析时长1 s条件下,正常、断齿-磨损和点蚀-磨损每种状态各40个振动信号作为测试样本。随机选取1组不同状态下齿轮振动信号,按本文处理步骤计算所得关联维数的结果如图9所示。 由图9可知,当嵌入维数为6~9时,各状态区分明显,因此特征值选取其关联维数均值。不同状态下40个测试样本关联维数的均值如图10所示。由图10可知,基于VMD和AR模型的关联维数对齿轮复合故障具有较好区分能力,在选定嵌入维数上的关联维数均值可有效对齿轮的故障类型进行识别。从而验证本文所提方法可有效用于齿轮复合故障状态的诊断。 齿轮发生故障时,其振动信号呈现出非线性特性并伴随大量噪声干扰成分,采用传统非线性特征刻画参数难以准确提取故障特征。VMD是一种自适应、非递归式信号分解方法,利用其将齿轮振动信号分解为多个IMF分量,并根据频域互相关系数准则滤除信号内的背景噪声重构信号,对重构信号建立AR模型并获取自回归参数,实现了齿轮故障信号线性化处理,保证了关联维数的计算准确性。通过齿轮的单一故障和复合故障的分析,证明了所提方法的实用性和可行性。2 试验研究
2.1 信号采集
2.2 信号预处理
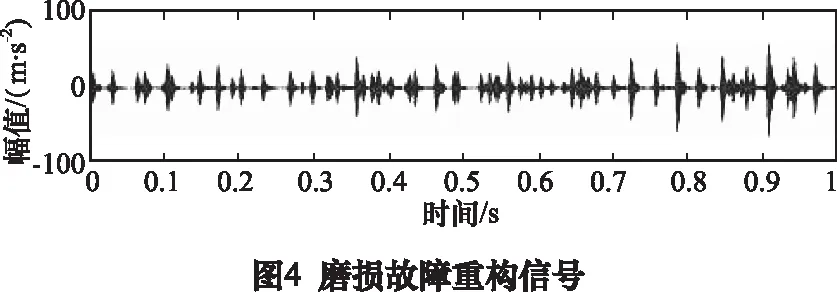
2.3 单一故障的齿轮信号特征提取
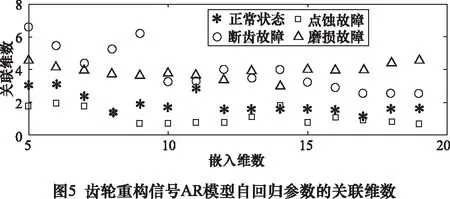
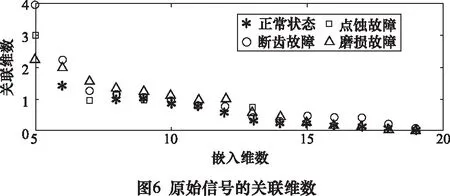

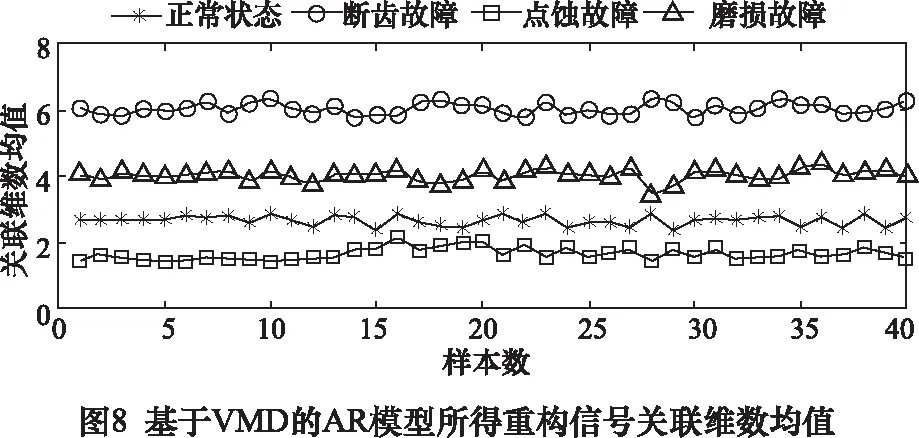
2.4 复合故障的齿轮信号特征提取
3 结语
