基于虚拟材料的滚珠丝杠进给系统建模及其时变特性研究*
2021-01-06陈勇将汤文成华洪良刘宵阳
陈勇将 汤文成 郭 魂 华洪良 刘宵阳
(①常州工学院航空与机械工程学院,江苏 常州 213032;②东南大学机械工程学院,江苏 南京211189)
滚珠丝杠进给系统被广泛应用于数控机床中,其性能直接影响着数控机床的加工精度与质量。在高速切削过程中,滚珠丝杠进给系统是时变系统,其动力学模型会随工作台位置和负载工件质量的变化而改变[1]。对滚珠丝杠进给系统振动特性、时变特性等动态特性进行研究,建立其准确的动力学模型至关重要。
滚珠丝杠进给系统动力学模型主要包括集总参数模型、混合模型和有限元模型[2-3]:集总参数模型不能分析系统的时变特性;混合模型只对丝杠采用连续弹性梁模型,其他部件简化成集中质量和弹簧阻尼单元,模型精度较差;有限元模型精度较高,但建模难度大。结合部模型的精确构建是进给系统混合与有限元模型准确建立的共性问题,其模型误差是系统结构动力学建模误差的主要来源[4]。因此,要建立准确的滚珠丝杠进给系统动力学模型,关键在于构建精确的结合部动力学模型。
在机床结合部建模方法中,基于虚拟材料的建模方法具有较高的精确性、较广的适用性和较强的实用性[5],因此,对此结合部建模方法开展的研究也越来越广泛和深入[6-10]。然而,基于虚拟材料结合部建模的研究仍停留在部件级分析阶段,对于滚珠丝杠进给系统不能只重视各结合部孤立的研究,更要开展系统级的结合部虚拟材料模型建模研究,才能建立准确的滚珠丝杠进给系统动力学模型。
1 滚珠丝杠进给系统动力学模型的建立
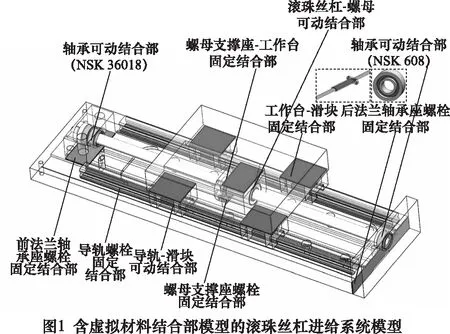
滚珠丝杠进给系统主要包括滚珠丝杠副、轴承及导轨等零件,它存在螺栓固定结合部和滚珠丝杠-螺母运动结合部、滚动导轨-滑块运动给合部与轴承运动结合部两种类型。基于虚拟材料的结合部动力学参数化建模法,滚珠丝杠进给系统固定结合部和运动结合部虚拟材料模型示意如图1所示。
采用多目标优化算法获得系统结合部虚拟材料模型的参数是一种有效的参数获取方法[11-12]。以仿真固有频率和试验固有频率之间差值的最小化目标函数计算模型,如式(1) ,选择带精英策略的非支配排序的遗传算法(NSGA-II)作为多目标优化算法。基于分形理论建立系统结合部虚拟材料模型参数的解析模型,以此解析模型求解得到的动力学参数变化范围作为约束条件。针对滚珠丝杠进给系统结合部虚拟材料参数的获取,基于多目标优化方法获取其参数可采用单独和整体两种获取方法。
(1)
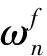
1.1 结合部虚拟材料模型参数的优化初值
滚珠丝杠进给系统结合部虚拟材料模型参数主要包括弹性模量、泊松比、密度和厚度。栓接固定结合部虚拟材料层的厚度一般约为1 mm,滚动导轨-滑块与轴承运动结合部的厚度值为滚珠直径值,滚珠丝杠-螺母运动结合部厚度值为螺母内径与丝杠外径差值,所以设计变量为弹性模量、泊松比和密度。考虑微凸体接触变形存在的三个阶段,基于两微接触点之间互相作用的弹性模量求解公式,可得到虚拟材料结合部的弹性模量求解公式为[5]
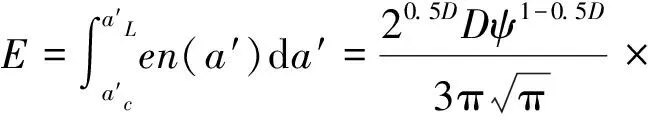
(2)
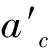
结合部虚拟材料的泊松比解析模型建立的关键是切变模量的构建,泊松比的表达式为
(3)
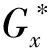
结合部虚拟材料的密度常用平均密度计算公式来计算:
(4)
式中:m1、m2分别为两工件微凸体层的质量;V1、V2分别为两工件微凸体层的体积;ρ1、ρ2分别为两工件微凸体层的密度;h1、h2分别为两工件微凸体层的厚度;Aa为结合面的名义接触面积。
1.2 结合部虚拟材料模型参数获取的多目标优化方法
针对滚珠丝杠进给系统结合部虚拟材料参数的获取,基于多目标优化方法获取其参数可采用两种方法:一是单独获取到各结合部的虚拟材料参数,即设计变量为单个结合部的弹性模量、泊松比、密度和厚度,目标函数为含单个结合部试件的仿真固有频率和试验固有频率之间差值的最小化;二是整体获取到全部结合部的虚拟材料参数,即设计变量为全部结合部的弹性模量、泊松比、密度和厚度,目标函数为系统整机的仿真固有频率和试验固有频率之间差值的最小化。
2 滚珠丝杠进给系统建模方法验证
为了验证基于虚拟材料方法建立的滚珠丝杠进给系统模型,搭建了如图2所示的滚珠丝杠进给系统模态测试平台,此平台主要由力锤、三轴加速度计、数据采集器、实时动态分析模块以及计算机组成。被测量滚珠丝杠进给系统主要结构参数见表1。实验测量:螺母在3个不同位置时的进给系统固有频率与振型,螺母移动位置的参照面为靠近前法兰轴承座的导轨起始端面,如图2所示,螺母位置1处、2处和3处距导轨起始端面分别为0 mm、115 mm和230 mm;含单个结合部试件的固有频率与振型。
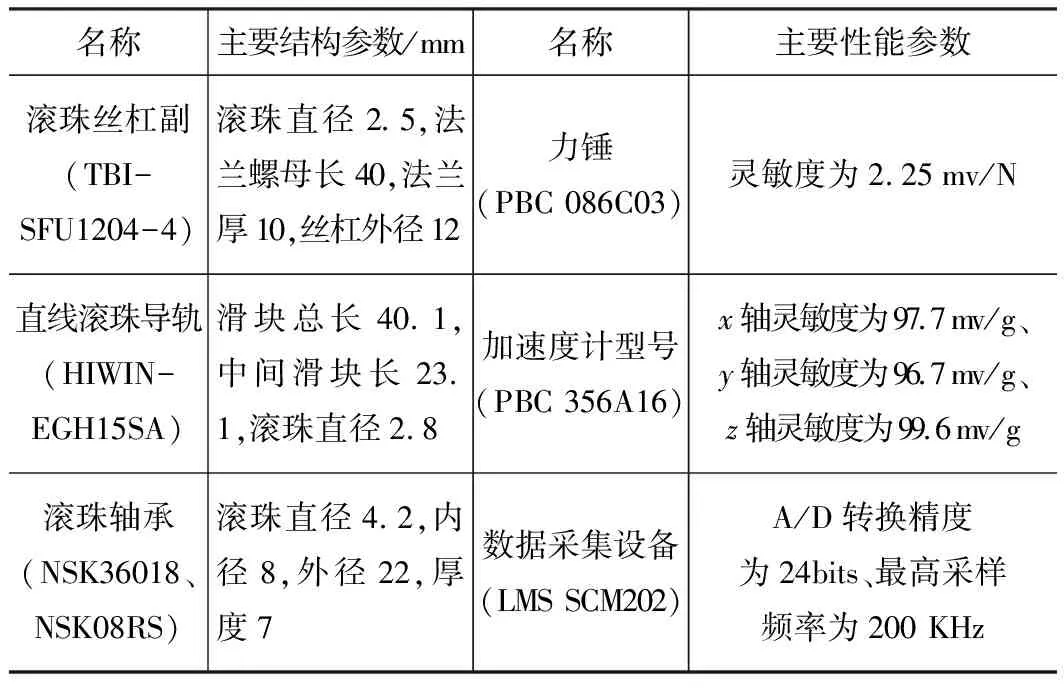
表1 滚珠丝杠进给系统模态测试平台主要参数
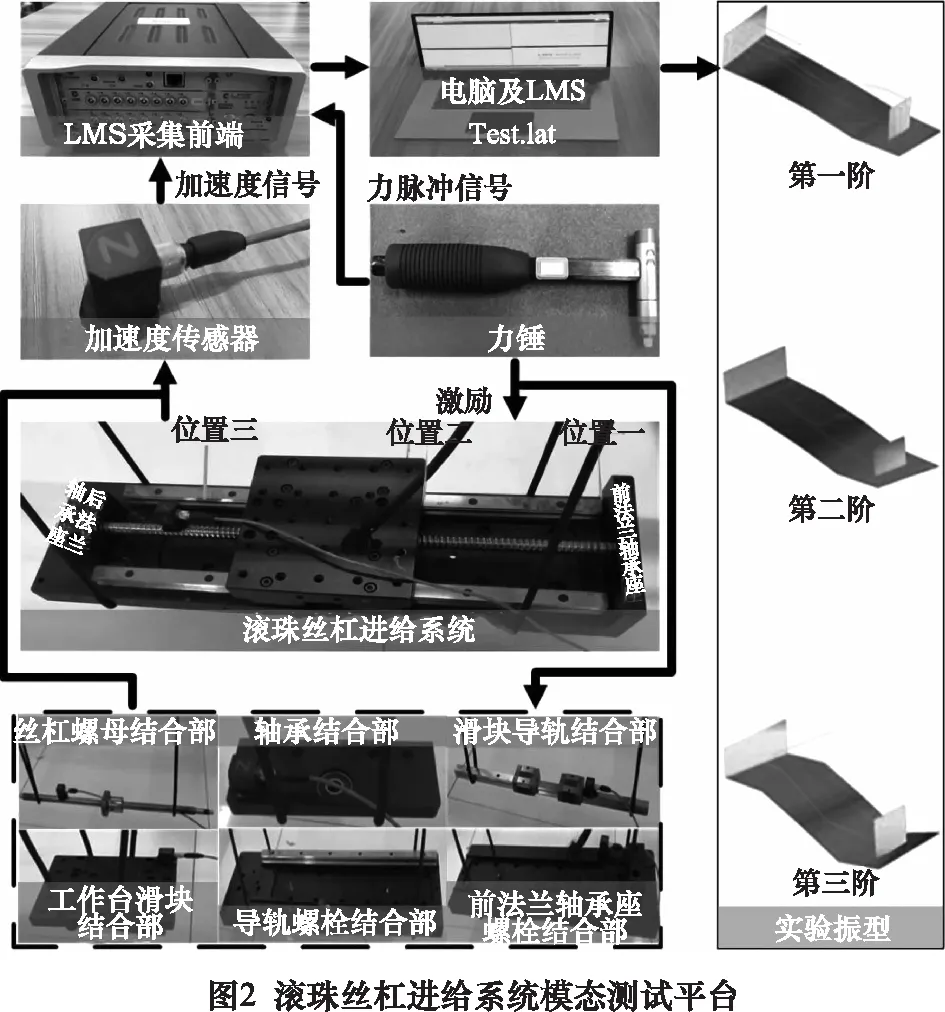
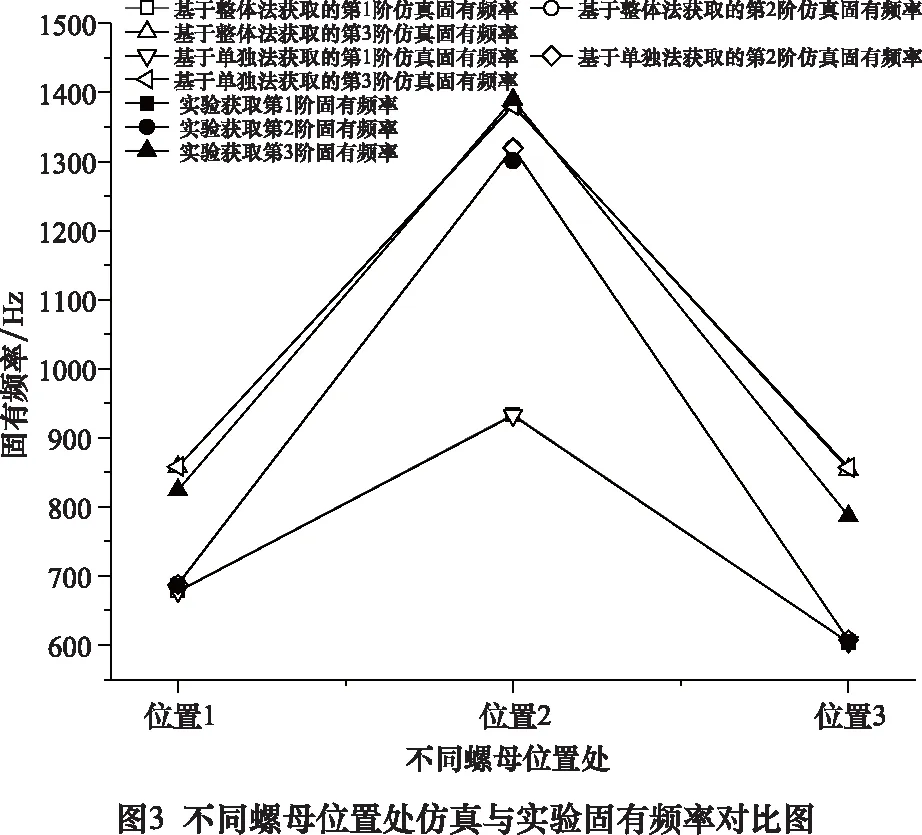
模态实验采用移动力锤法,传感器安装在丝杠上,通过橡皮绳悬挂滚珠丝杠进给系统试件来模拟自由边界条件,在试件上布置了32个激励点。根据模态有效质量比计算结果可知,需取3阶试验固有频率参与到目标函数的优化过程。通过对比试验模态振型与理论模态振型的相似性,确定此3阶试验固有频率具体选择的阶数。由获得的实验振型可知,在3个不同螺母位置处,皆有一阶与滚珠丝杠进给系统仿真振型对应的实验振型未获取到,分别为螺母位置1处、2处及3处的第2阶、第1阶及第2阶实验振型。同时可知,滚珠丝杠进给系统前3阶振型,以丝杠的弯曲振动为主,伴有底板的扭转振动。由图3可知,基于滚珠丝杠进给系统虚拟材料动力学模型仿真得到的固有频率与模态实验获取的固有频率基本吻合,且基于整体获取法获取参数的仿真固有频率更为接近实验固有频率。
3 讨论
3.1 两种方法获取的结合部虚拟材料模型参数的对比与分析
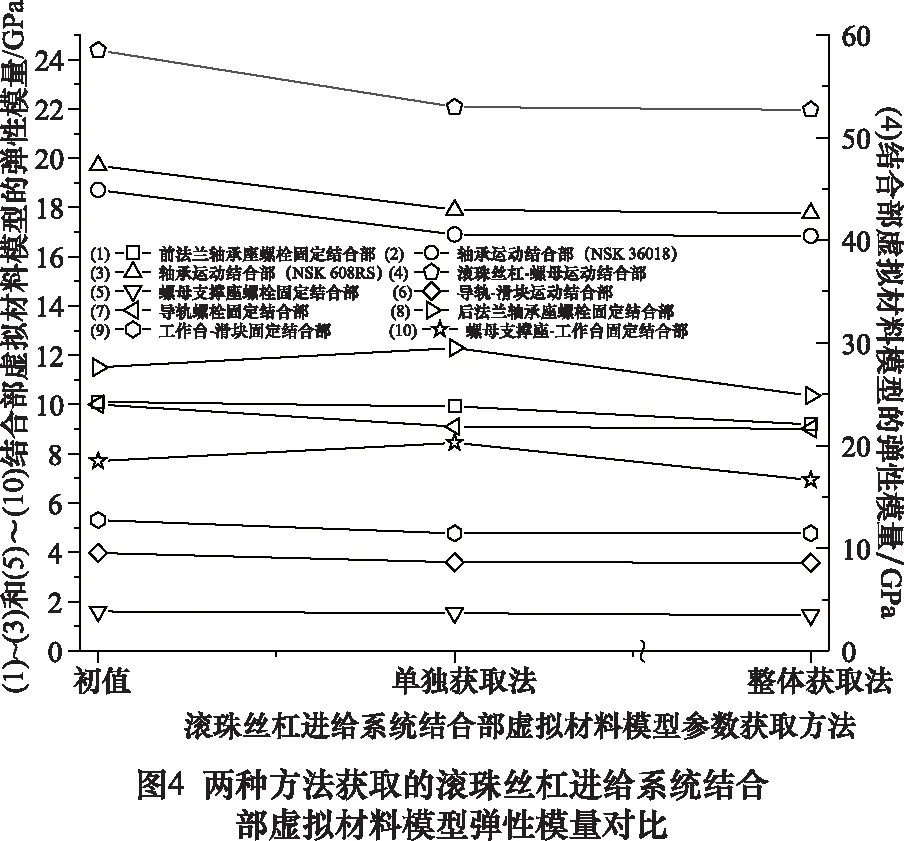
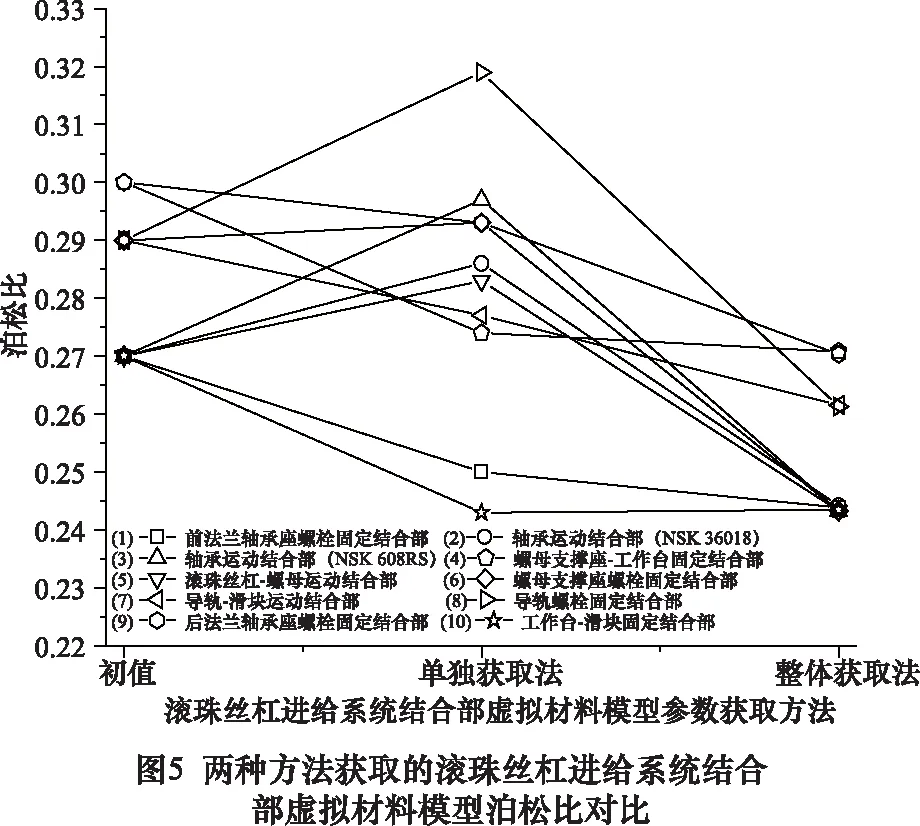
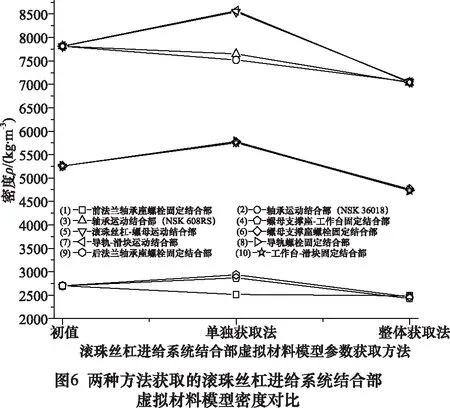
由图4~6可知,基于多目标优化方法整体获取的结合部虚拟材料模型参数值都小于初值和单独获取法的获取值,这主要是由于整体获取法的目标函数为系统整机的仿真固有频率和试验固有频率之间差值的最小化,而滚珠丝杠进给系统整机固有频率较绝大部分单独部件的固有频率低(含各结合部的单独部件固有频率,以下简写成“各结合部的固有频率”)。
同时可知,基于多目标优化方法单独获取各结合部虚拟材料模型参数值相较于整体获取法的获取值有着一定的分散性,这与单独获取法目标函数为各结合部试件的仿真固有频率和试验固有频率之间差值的最小化有着直接关系。因为各结合部试件的固有频率都不一样,而整体获取法的获取值相对集中于3个区域,尤其是结合部虚拟材料模型的泊松比和密度,这与选取3阶试验固有频率参与到目标函数的优化过程不无关系。滚珠丝杠-螺母运动结合部虚拟材料模型的弹性模量值最大,由已有研究可知,滚珠丝杠进给系统中滚珠丝杠-螺母结合部接触刚度相对较大,从宏观角度看弹性模量可以表征结合部的接触刚度。
3.2 螺母位置与负载质量对进给系统振动的影响
由上可知基于整体获取法获取的滚珠丝杠进给系统结合部虚拟材料参数,将其获取的参数代入至仿真模型,据此分析不同螺母位置与负载质量对进给系统动态特性的影响。在高速切削过程中,螺母位置与负载质量在不断变化,这种变化会影响滚珠丝杠进给系统的振动模态。由图3可知,随着螺母位置从位置1移至位置3,即螺母远离参照面的过程中,滚珠丝杠进给系统的前三阶固有频率皆先变大后减小。在螺母位置2处,即丝杠中间位置处的前三阶固有频率最大。这是由于螺母扮演了移动弹性支撑的角色,其位置变化会导致进给系统的刚度跟随其产生相应的变化:当螺母处于丝杠两端时,系统的总体支撑刚度最小;当螺母处于丝杠中间位置时,系统总体支撑刚度较大,其固有频率也就越高。由图7可知,工作台负载质量越大,系统刚度越小,系统的固有频率越小。工作台负载质量对进给系统固有频率虽有影响,但不如螺母位置对进给系统固有频率的影响。

4 结语
(1)基于多目标优化方法单独获取各结合部虚拟材料模型参数的获取方法计算量小,但操作繁杂,需要对各个结合部都进行试验模态分析与仿真模态计算。基于多目标优化方法整体获取全部结合部虚拟材料模型参数的获取方法计算量大,需要同时优化全部结合部的参数,但操作简单,只需对滚珠丝杠进给系统进行一次试验模态分析与仿真模态计算,并通过实验证明其获取参数更为可靠。
(2)由于整体获取法基于系统整机的固有频率,故基于多目标优化方法整体获取的结合部虚拟材料模型参数值都小于初值和单独获取法的获取值。
(3)随着螺母位置和工作台负载质量的改变,滚珠丝杠进给系统的动力学模型具有时变特性。工作台负载质量对进给系统固有频率虽有影响,但不如螺母位置对进给系统固有频率的影响。
