人工智能技术的教学讨论*——以粒子群算法为例

肖文波 叶国敏 陈 敏 程小金 龚勇清

(南昌航空大学国家级大学物理实验教学示范中心 江西 南昌 330063)

随着世界上人工智能教学的快速发展[1],国内《新一代人工智能发展规划》提出：人工智能教育培养日益迫切.不仅高校提倡人工智能应用于教学[2],更有中小学开设人工智能课程[3].将人工智能纳入教学中,不仅推动了人工智能与教师教育的深度融合实现高效管理[4,5],而且推进了人工智能与教育的共生发展[6,7].当前研究关注人工智能应用中某一课程或者某一专业教学改革方面,例如人工智能与统计学课程[8]、麻醉学专业等结合[9].而实际上,人工智能教学不能仅停留在知识获取、技能学习上,还需要聚焦创新能力的培养[10,11].由此有研究探讨了人工智能课程中的基本算法与模型,培养学生基本知识与解决问题能力[12].但仍然缺乏以人工智能教学为基础,分析并讨论其中问题及注意事项.

为此,本文以人工智能技术中粒子群算法为基础,讨论了人工智能基本原理;并应用于基于光伏发电最大功率点的跟踪[13],探讨了粒子群寻优算法的建立原理与方式,结合教学及学生学习心得总结出了教学注意事项.该研究为人工智能技术的教学与实践提供参考.

1 粒子群算法介绍

人工智能技术是模拟思维过程和智能行为(如学习、推理等)的学科,主要是通过逻辑思维来不断学习与进步.人工智能技术中粒子群算法是1995年Kennedy和Eberhart首次提出,是通过模拟鸟群觅食行为发展而来的一种多极值函数全局优化方法[14～16].实际上,粒子群智能算法教学目标有3个方面：

第一，学生能够理解粒子群算法的基本概念以及流程.

第二，学生能够掌握粒子群算法的实现原理及模型公式.

第三，学生能够知道影响粒子群算法的主要参数.

下面就围绕上述3个目标阐述.

1.1 粒子群算法的流程

粒子群算法的基本流程如下.

第一步，初始化粒子,首先初始化粒子群算法中各个参数的数值,主要包括种群规模、学习因子、惯性权重等.

第二步，评价粒子,由适应度函数计算出粒子的适应值.

第三步，寻找群体中的个体最优值和全局最优值.

第四步，更新粒子的位置和速度.

第五步，重新计算粒子的适应度值并和之前的比较.

第六步，更新个体最优值与全局最优值.

第七步，检验是否终止,如果搜索结果达到收敛精度或者是设定迭代次数,那么迭代终止并输出最终解.如果不满足,就跳转至第四步继续迭代计算.

具体过程如图1所示.

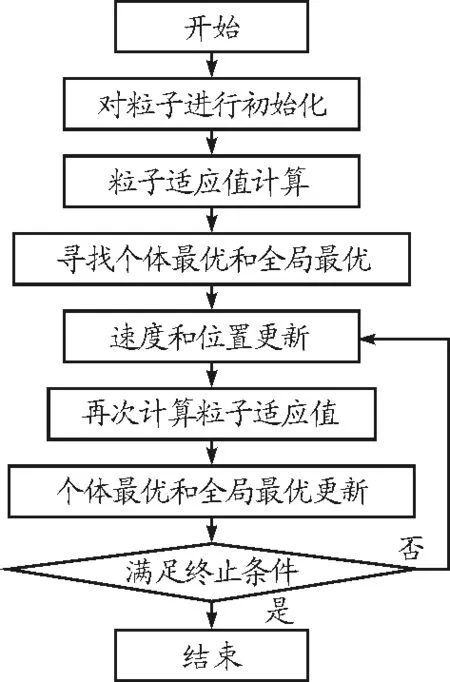
图1 粒子群算法流程图

1.2 算法实现原理及模型公式

算法实现原理是通过迭代找到最优解,在种群规模N的粒子群中迭代,粒子通过跟踪两个“极值”来更新自己.第一个就是粒子本身所找到的最优解,另一个极值是整个种群找到的最优解,即全局极值.

找上述两个最优值时,根据如下的公式来更新自身的速度(v)和位置(x).

(1)

(2)

式中,ω为惯性权重,d表示搜索空间维数,i表示粒子序号,c1和c2为学习因子,r1和r2为(0,1)之间均匀分布的随机数,t表示迭代次数.Pbest表示个体最优值和Gbest表示全局最优值.每次迭代中,速度都限制在[-vmax,vmax]内.群中每个粒子都从初始速度与位置开始,按照上述公式迭代计算,直到满足条件.

1.3 粒子群算法中主要参数

由上述原理与模型公式,可以看出算法中参数有着重要的意义,将会直接决定算法的终止时间以及精确度等.以下将介绍算法中典型参数意义.

种群规模N：算法的收敛时间受种群规模大小的直接影响,如果N比较小,那么算法很有可能陷入局部极值,但是收敛时间较短;当N很大时,算法的精确性与收敛性提高,但是也会增加计算的复杂度.

粒子的最大速度vmax：合理的最大速度可以避免算法迭代时出现发散.vmax较大时,虽然粒子的寻优速度快,但是越过最优值的可能性较大.如果vmax过小,虽然不会越过最优解,但是粒子搜寻速度过慢并且容易限于局部极值难于摆脱,降低算法效率.

惯性权重ω：粒子群算法中最为重要的研究参数.算法的初始阶段,较大的ω能够防止算法陷入局部最优,在算法的后期,较小的ω能够提升收敛速度,并且使收敛更加平稳.

学习因子c1和c2：c1调整粒子飞向个体极值的比重,c2调整粒子飞向全局极值的比重.学习因子比较小时,会导致粒子在接近目标区域时被拉回;学习因子较大时,粒子搜索速度太快导致越过目标地区.

2 粒子群算法应用

2.1 遮荫下光伏发电最大功率点的获取

对1×2串联光伏阵列的8种遮荫下最大峰值功率进行跟踪,阵列在遮荫下光伏发电原理[17,18]的Matlab/Simulink仿真数据如表1所示.表1是串联光伏阵列中第一块电池和第二块电池的光照强度不同,对应的每一种遮荫下峰值功率也不一样.

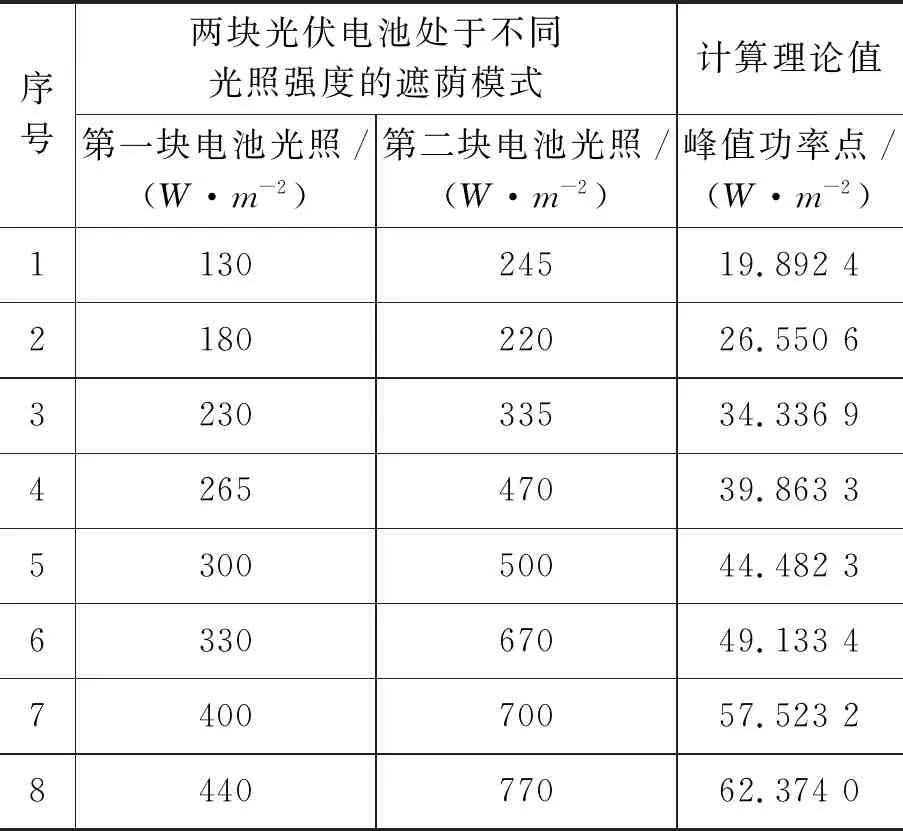
表1 八种遮荫模式下电池功率及其峰值电压

2.2 采用粒子群算法寻优时参数影响的讨论

粒子群算法中的参数将影响人工智能技术的性能,为此教学中需讨论参数对寻优的影响规律.对上面8种遮荫下峰值功率进行寻优,主要通过改变种群规模、学习因子、惯性权重、最大速度等参数,讨论了平均跟踪时间与峰值功率跟踪精度变化.

2.2.1 种群规模

根据调整种群规模的大小,来分析种群规模对粒子群算法的速度和精度的影响,设置了5组种群规模,其具体结果如表2所示.

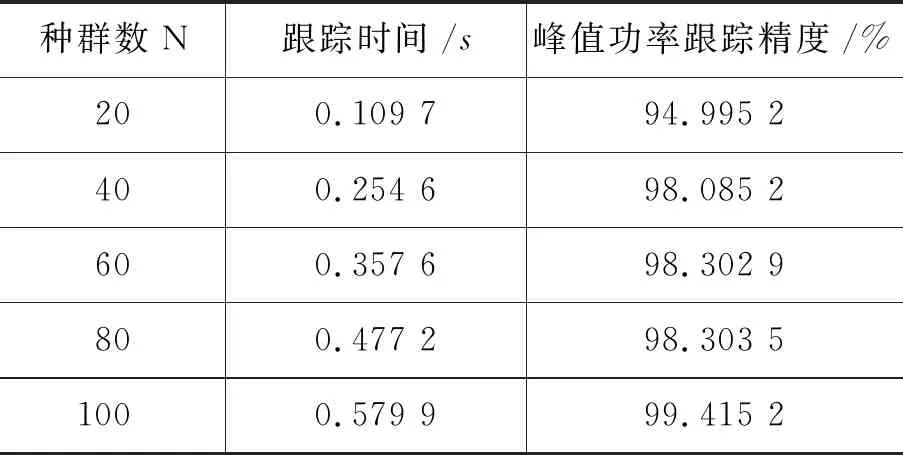
表2 不同种群规模下算法寻优的跟踪

由上表可知,种群数目从20到100时,时间从0.109 7 s增加至0.579 9 s,峰值功率跟踪精度从94.995 2%增加至99.415 2%.综上所述,种群越大速度越慢,搜索精度越高.

2.2.2 学习因子

设置了5组学习因子,来分析学习因子对算法速度和精度的影响,具体结果如表3所示.

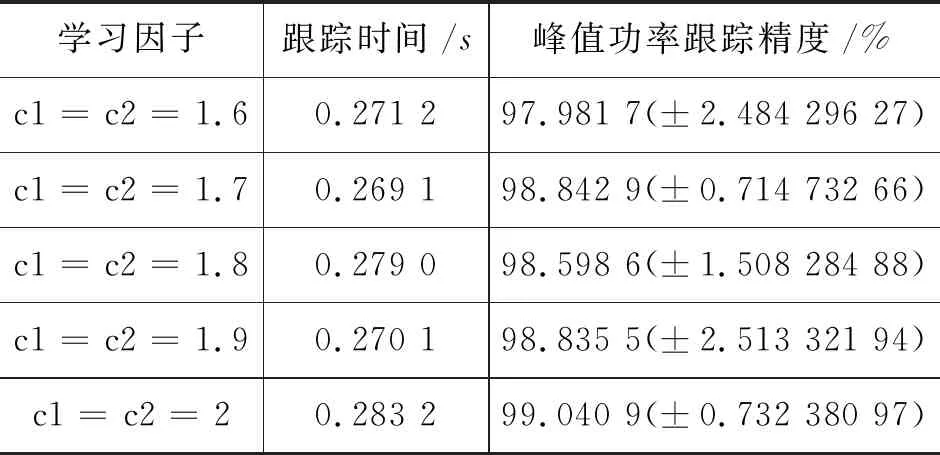
表3 不同学习因子下算法寻优的跟踪

由上表中跟踪时间上看,当c1=c2=1.7时,粒子群算法的跟踪时间在所设5组中是最短的;从峰值跟踪精度上看,当c1=c2=2时,其粒子群算法的峰值精度在所设5组中是最高的.由此,可知合理的学习因子可以减少跟踪时间,提高跟踪精度.此外,可知跟踪时间越长,其精度越高.

2.2.3 惯性权重

设置了5组惯性权重,来分析惯性权重对粒子群算法速度和精度的影响,具体结果如表4所示.

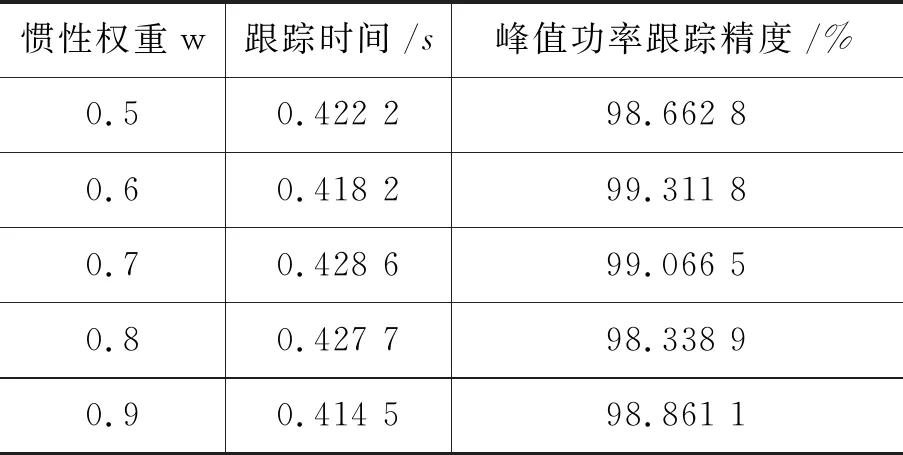
表4 不同惯性权重下算法寻优的跟踪

由上表中跟踪时间、精度可以看出,惯性权重在0.6～0.7中,其展现出的性能更为稳定,虽然时间不是最佳,但是其精度是最好的.优化的惯性权重有利于粒子群算法的搜索.

2.2.4 最大速度

设置了5组最大速度,来分析最大速度对粒子群算法速度和精度的影响,具体结果如表5所示.

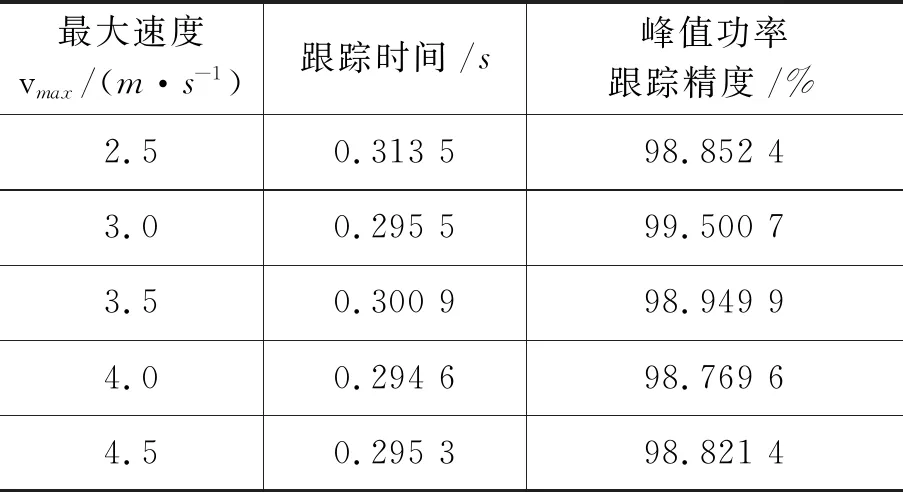
表5 不同最大速度下算法寻优的

从上表可以发现,最大速度vmax=3 m/s时,精度是最高的,当最大速度vmax=4 m/s时,其跟踪时间最短.综上所述,最大速度在2.5～4.5 m/s中时,粒子群算法的跟踪时间与精度方面有优势.

3 教学讨论

上述智能算法技术平台搭建好后,应用于教学过程中;根据学生认识、熟悉和掌握算法的程度以及实验后的讨论,得出开展该类算法实验需要注意的事项,并总结了提高教学效果的途径.具体如下.

(1)在实验之前,较多学生对算法相关知识与基础预习少,导致他们对实验内容还是不清楚且很难理解到实验的真谛,这就有悖做实验的目的.所以,该类实验也会降低教师的授课质量,增加教学难度.为了提高教学质量,任课教师最好通过网络手段在课前给学生们提供相关知识的指导,例如通过QQ、微信平台、邮件等发相关资料给学生们,并提醒他们及时预习.

(2)实验中的重点、难点是具体问题与人工智能算法结合时的知识表示.本文中结合粒子群算法对遮荫下光伏发电最大功率点的预测是实验内容,但明确算法的流程及其原理是目的.重点是培养人工智能与具体应用的结合能力.由于部分学生缺乏光伏发电最大功率点的预测知识,并且纠结于matlab/simulink软件上实现各种仿真模块的使用，导致他们对算法结论的理解不足,无法体会到算法的特点等.所以,该类实验教学中,应该重点强调教学结果的讨论,以便学生得出明确结论.

(3)人工智能算法与传统学科最大的区别在于,传统学科的知识体系大都是公式化的.而目前人工智能算法是概率化、训练化的.尤其是该类算法可以和学生的兴趣爱好、生活习惯等结合,应用算法来分析各种具体问题.此外,还要引导学生对算法本身思考,具体就是在选择知识表示时应该考虑的影响因素及规律有哪些？建立正确的分析模型.而不只是编程操作一下.

(4)实验的教学手段中,除了相关理论知识的讲解,当然实践操作也很重要.编程算法过程中,碰见问题,任课教师不要简单粗暴地直接回答问题,而应该引导学生们之间互动地解决问题.互动学习更能增加学生的热情,让学生投入到实验中去.

总之,尽管人工智能教学目前很“火”,但重要是帮助学生将人工智能置身于智能科学的大背景中,既包含了自然智能、计算智能等学科,更要包括逻辑判断、非线性处理等学科.此外,也提醒教育管理者要进一步完善人工智能相关课程体系的配置和优化.

4 总结

人工智能技术的建立及其特征的教学讨论,有利于学生理解相关知识.为此,本文以粒子群算法为例,结合遮荫下光伏发电最大峰值功率跟踪进行了阐述,并讨论了教学注意事项.通过上述教学讨论,得出及时预习相关基础知识有利于学生理解人工智能技术,结合具体问题讨论人工智能算法将有利于学生掌握技术,拓展人工智能技术应用范围并引导学生对算法本身思考将有助帮助学生建立正确模型,建立互动式解决实验问题将增加学生的学习热情.