堆积刚性链条下降的多次碰撞求解*

赵 斌 吴庆春 汪连城 金远伟

(南京工程学院数理部 江苏 南京 100875)

链条下落运动是典型的变质量体系，一直备受广大师生的关注，它也是大学物理“质点系动量定理”教学中常选用的典型问题[1,2]．链条下落时，没有碰撞时是自由下落(图 1)．文献[2]指出了这一下落过程中能量损失的原因是链条间的非弹性碰撞．本文仍只考虑下落速度与下落链条长度的函数关系，我们采用碰撞的节点处速度是不连续的描述，即引入第一类间断点或者跳跃间断点．由于链条是刚性，链条碰撞过程是完全非弹性碰撞，我们细致推导给出了下降过程中每下降一段链条的能量损失和下落过程的总能量损失，并计算了下落时间、加速度．当链条分段足够小时，即通过求极限给出了柔软绳的结果．

1 链条下落问题和动量定理的求解

为了后面工作的对比参考，这里我们首先简介一下大学物理中链条下落问题和动量定理的求解过程[2]．如图1所示，初始一柔软刚性链条单位长度的质量为λ，链条放在有一小孔的桌上，链条一端由小孔稍伸下，其余部分堆在小孔周围．由于某种扰动,链条因自身重量开始下落.求链条下落速度v与下落距离y之间的关系．

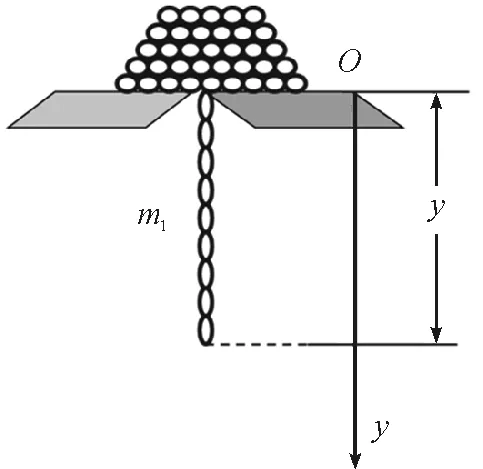
图1 柔软链条下落示意图，竖直向下为Oy轴正向

设各处摩擦均不计，且认为链条软得可以自由伸开．动量定理的求解如下：在t时刻，设链条的下垂长度为y，下落速度为v，下垂部分的质量m1=λy．该部分链条的动量

p=λyv

外力冲量

Fexdt=m1gdt=λygdt

利用质点系的动量定理(Fexdt=dp)有

λygdt=λd(yv)

上式两边同时乘以v，得到

λgydy=λvd(yv)

替换变量，两边积分

给出了v与y的关系

由此算出下落长度为y的过程中机械能总的损失为

2 多次碰撞下落的求解模型

假设均匀、离散的链条每一截链的长度为Δl, 质量为m0，则单位长度的质量

在第ti时刻，下垂了i节链条，此时，该下垂部分的长度iΔl, 记为位置坐标yi=iΔl， 质量为im0=λyi.由于下落中的碰撞过程，位置yi点，速度不连续，即此位置处左右极限不相等,为跳跃间断点，记为

这里用速度在yi处的左右极限表示该位置发生碰撞前后的速度值， 由于是刚性链条，碰撞前后下落链条的质量从im0变成(i+1)m0．在这个过程中第(i+1)段小链条突然受到了已下落i节链条的脉冲力，然后整体一起下落运动．这可以视为一个碰撞过程，而且是完全非弹性碰撞．碰撞前后速度发生了跃变，即在同一位置处速度不连续，为间断点．根据动量守恒，则碰撞前后瞬间的速度关系为

考虑第i(i≥2)节链条从yi+到y(i+1)-的下落过程中[yi+表示在位置yi完成碰撞，y(i+1)-表示在y(i+1)处还未碰撞，yi=yi-=yi+]，整体做自由落体运动，有

(1)

于是利用式(1)和上面的动量守恒得到的vi-和vi+递推关系，我们可以计算出

利用数列求和公式[3]可以得到

(2)

(3)

在i足够大的极限情况下，式(2)、(3)同时趋近于连续的计算表达

利用式(2)、(3)，我们可以很容易计算第i次完全非弹性碰撞过程损失的机械能δei

(4)

由于非弹性碰撞，损失的机械能量转化为热． 第i次下落过程中，i节链条先是整体自由下落Δl，获得的动能增加为λgyiΔl，随后第i碰撞损失的机械能为δei，δei相对于第i(i≥2)次下落获得的动能之比(ξi)为

(5)

的微分可以得到

可以看出这与式(5)的极限表述是一致的．

利用表达式(4)，我们对i求和可以计算下落到yn位置链条总共损失的机械能

整理可以写成

(6)

我们发现式(6)对所有n都成立(包括n=1)，当n足够大时，式(6)正是前面动量定理给出的结果．

由下落速度的表达式(2)、(3)可以计算第i次下落需要的时间Δti，由于第i次下落过程中，i截链条整体自由下落Δl，速度由v(i-1)+增大到vi-，则

(7)

同样，通过求和得到下落到yn处的需要下落时间

(8)

表达式(8)是下落n段链条需要的时间．对于不同的n值, 可以计算得到

随着n增大，表达式(8)是收敛的．由连续软绳的计算结果

可以得到下落的加速度

下落时间与下落位移y的函数关系为

令y=yn，定义相对误差

我们可以通过数值计算相对误差来考察表达式(8)的收敛性：n=1 000，δtn=0.023；n=105,δtn=0.002 4；n=106,δtn=7.5e-4．可以看出当n趋近无穷大时，表达式(8)收敛为

前文已经提到，在刚性链条下落的过程中，除去下落节点的位置处，下落的加速度都是g．由于我们引入了速度间断的模型，自然会导致下落节点的加速度是奇点．这里我们可以通过定义一个链条下落过程的平均加速度来回避节点的奇性．定义第i个链条完整下落过程的平均加速度

(9)

由于是刚性链条，碰撞是瞬时的，将式(7)的下落时间代入式(9)可以得到

(10)

3 结论

我们严格推导了堆积刚性链条下降的多次碰撞求解的明确表达，给出了从离散到连续的数学表述．其中一系列完全非弹性碰撞的严格计算有助于学生理解相关变质量系统的物理过程，以及培养学生建立不同数学模型求解物理问题的能力．