MATLAB编程在层合板强度分析中的应用1)
2021-01-06董纪伟陈培见程红梅罗宁张桂民
董纪伟 陈培见 程红梅 罗宁 张桂民
(中国矿业大学力学与土木工程学院,江苏徐州221116)
强度问题是复合材料板力学性能研究和结构设计的核心问题之一。从分析尺度来看,板的强度分析包括宏观力学、细观力学和微纳米力学分析[1]。其中,层合板强度的宏观力学分析是复合材料力学课程的教学重点和难点。由于该问题理论性强、逻辑关系复杂、数学运算繁琐、手工计算量大,学生在学习时往往会产生畏难情绪,接受知识困难。另一方面,MATLAB以其强大的数学计算、符号运算、图形处理等功能和简单易学的编程语言,作为辅助手段可促进学生对知识的理解和应用,提升教学效果。目前,在力学基础课和专业课中已有许多应用MATLAB的成功案例[2-5]。本文将探讨一种基于MATLAB编程的层合板强度分析方法,通过该方法不仅可使问题的求解大为简化,还便于讨论主要参数对层合板强度的影响,为层合板的强度设计提供依据。
1 问题的提出[6]
如图1所示的三层正交铺设对称层合板,其正交铺设比m=0.2,总厚度为t,承受轴向拉力Nx作用。各单层材料为玻璃/环氧,其性能为:E1=54 GPa,E2=18 GPa,ν21=0.25,G12=8.8 GPa,Xt=Xc=1050 MPa,Yt=28 MPa,Yc=140 MPa,S=42 MPa。试用MATLAB求层合板的极限载荷Nx/t,并讨论正交铺设比对极限载荷的影响。
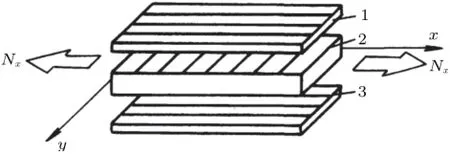
图1 三层正交铺设对称层合板示意图
正交铺设层合板单层刚度形式简单,强度分析的运算量相对较小,因此常作为《复合材料力学》教材中的典型例题[6]。然而,由于层合板破坏过程复杂,破坏形式多样,手工计算过程仍较为繁杂,且计算效率低,每次只能预测一种参数下的层合板强度。事实上,对于正交铺设层合板,正交铺设比m是影响其力学性能的主要参数,它表示0°层总厚度与90°层总厚度的比值。那么,既要研究正交铺设比对层合板强度及破坏规律的影响,从而对该类层合板进行合理的厚度设计,又要保证计算效率,手工计算显然是不可行的,而应采用参数化编程的方法对该问题进行分析。
2 层合板的强度分析及MATLAB编程
要将复杂的层合板强度分析通过计算机编程实现,首先应对强度分析过程中涉及到的基本理论和强度分析流程有一个清晰的认识,再将其转化为计算机语言进行计算分析。
2.1 层合板的单层应力计算
层合板的破坏是其单层板逐层破坏的过程,而大多数关于单层板的强度理论都是基于应力的理论,因此,单层板的应力计算是层合板强度分析的基础。基于经典层合板理论,层合板单层应力分析流程如图2所示。
首先,由各单层的正轴模量计算出层合板的正轴柔度矩阵S,然后对其求逆得到正轴刚度矩阵Q,如下所示
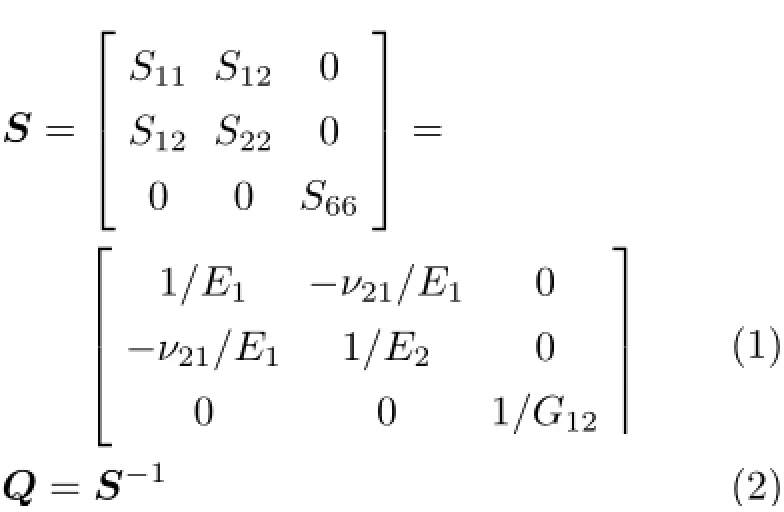
对于例题中的正交铺设层合板,0°层的偏轴刚度和正轴刚度相同,90°层的偏轴刚度只需将正轴刚度系数Q11与Q22互换,即
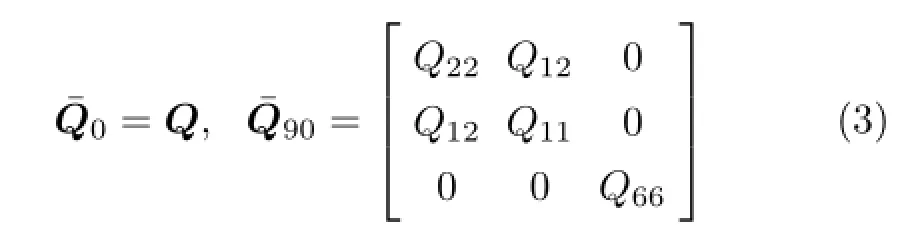
其次,计算层合板的刚度和柔度。对于正交铺设对称层合板,不存在拉弯或拉剪的耦合,因此单向受拉时只需计算其拉伸刚度A,对其求逆得到层合板柔度A′,计算公式为
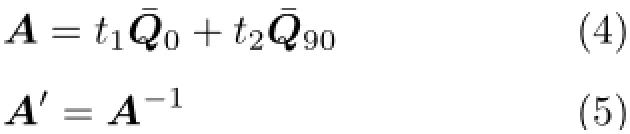
其中t1=mt/(m+1),t2=t/(m+1)。

图2 层合板单层应力计算流程图
再次,计算层合板的中面应变。在轴向拉力Nx下,该层合板的内力-应变关系为
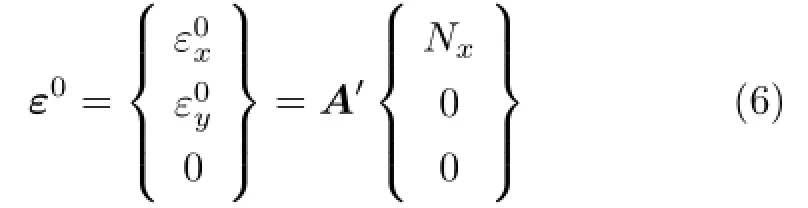
最后,计算各单层的应力。由单层的应力-应变关系得0°和90°层的应力分别为
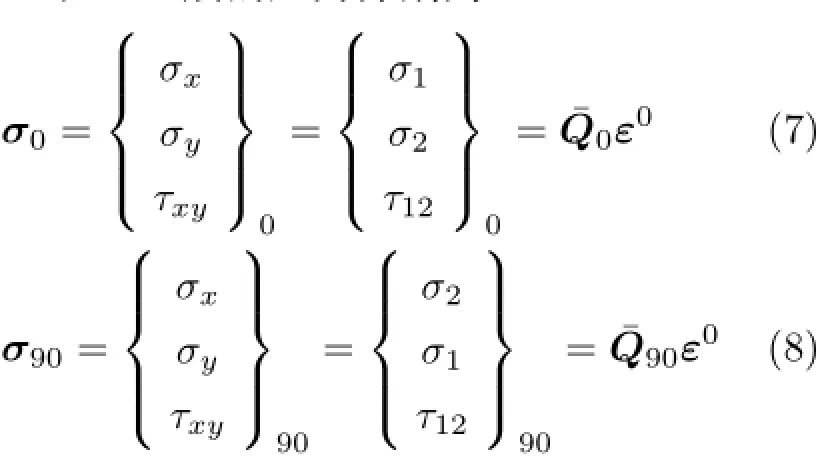
单层板的刚度及层合板应力的计算分别用两个函数文件表示,程序如下:

2.2 单层板的强度准则
进行强度分析时,需选择合适的强度理论判断各单层是否发生强度失效。考虑到单层板拉、压强度的不同,本文采用目前最流行的Tsai-Wu张量强度理论作为单层板的强度失效判据,其表达式为
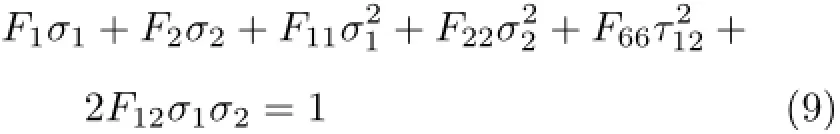
式中
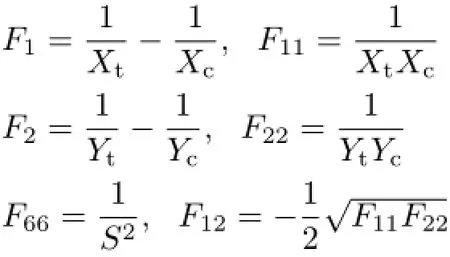
其中Xt和Xc分别表示纤维方向(纵向)的抗拉、抗压强度;Yt和Yc分别表示垂直纤维方向(横向)的抗拉、抗压强度;S表示面内剪切强度。
计算Tsai-Wu准则方程左边项的MATLAB程序如下:

2.3 强度分析流程
单层的破坏并不意味着整个层合板的破坏,但会使该单层的刚度降低,通常情况下采用刚度折减法对其进行处理。由于单层板的破坏具有各向异性,在对某破坏层进行刚度折减时,并不是将其所有的刚度系数都降为零,而应根据破坏类型对其刚度系数进行相应的折减,具体折减方案见表1。
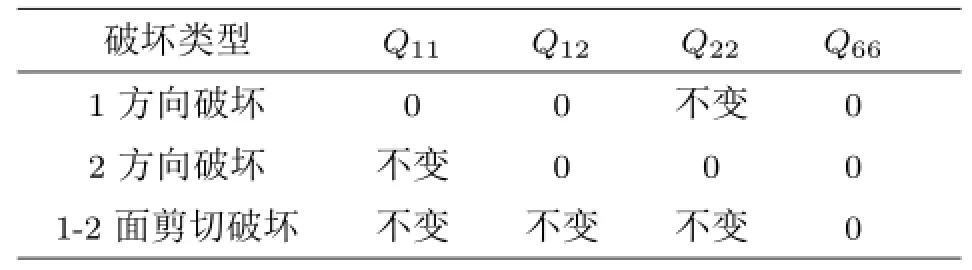
表1 单层板的刚度系数折减方案
表1 中,各单层的破坏类型可由最大应力理论确定。根据式(7)和式(8)计算出发生破坏单层主方向的应力,若某个应力分量接近相应的基本强度值时,单层板就沿该方向发生破坏。例如:若σ1>0,σ2>0,σ1<<Xt,σ2≈Yt,|τ12|<<S,则该层就沿2方向发生破坏。
对破坏的单层进行刚度折减后,应重新计算层合板的刚度和柔度,再检验是否有新的单层发生连锁破坏,如果有,则重复刚度折减的步骤,直到没有连锁破坏发生为止。接下来,由于层合板刚度的降低,使其载荷-变形关系变为非线性,应采用载荷增量法进行下一步的计算,即:假设载荷增量ΔNx,由式(6)~式(8)计算中面应变增量Δε0和各层应力增量Δσ,将此时各层的总应力σ再代入强度准则中确定下一次破坏时的载荷。以此类推,直到所有层沿加载方向均不能承载,则层合板最终破坏,此时的载荷即为层合板的极限载荷。
基于上述理论,例题中层合板强度分析的流程如图3所示。
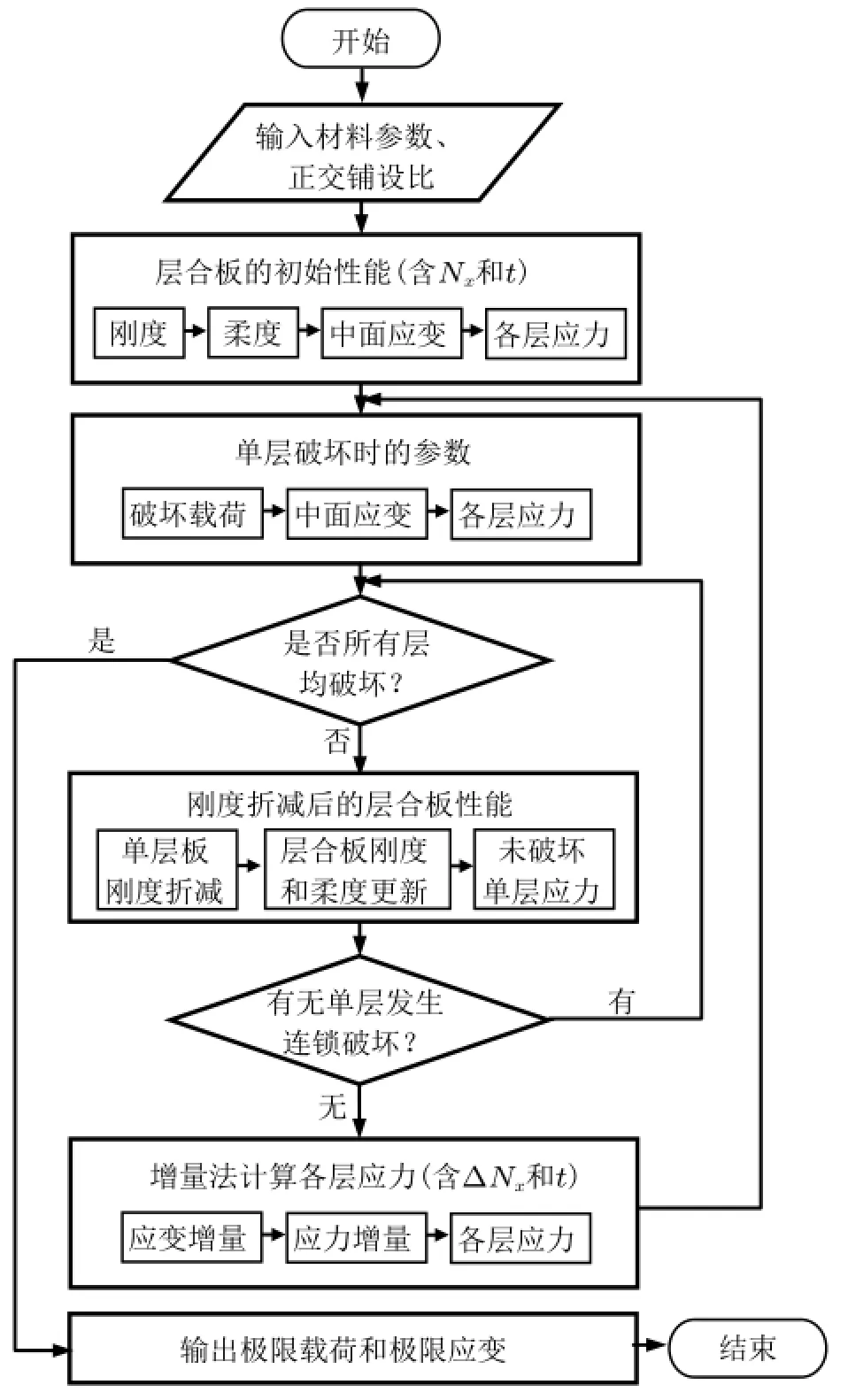
图3 层合板强度分析流程图
求解过程中,需根据Tsai-Wu准则确定单层破坏时的载荷Nx/t或载荷增量ΔNx/t,这就需要求解一元二次方程,手算比较困难,而利用MATLAB符号运算的功能比较容易实现,以求解首次破坏时的Nx/t为例,其程序如下
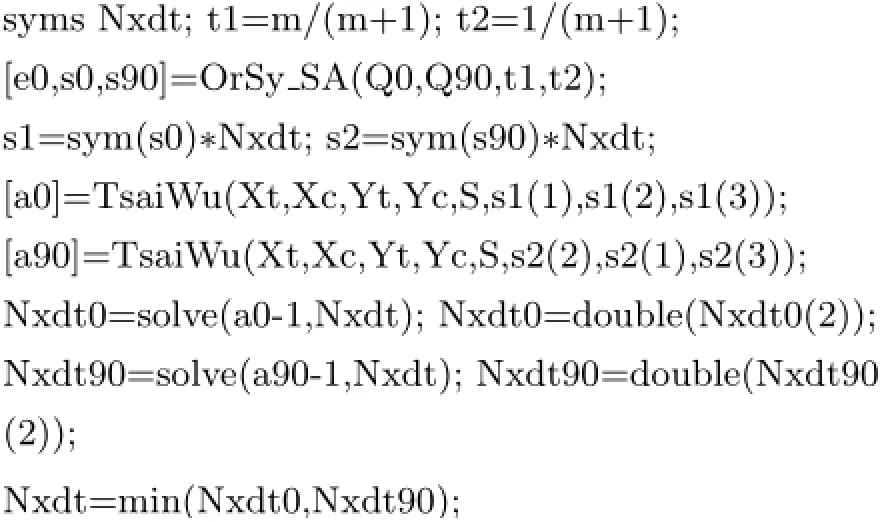
按照图3所示的分析流程,编制MATLAB主程序求解例题,函数文件为“function[ex,Nxdt]=OrSy TFA(E1,E2,miu21,G12,Xt,Xc,Yt,Yc,S,m)”,该函数返回的参数为层合板的极限载荷和极限应变,而计算过程中的铺层失效信息、每次破坏时的载荷和应变通过fprint语句输出到结果文件“fail.dat”中。
3 结果及讨论
编制完M文件后,在MATLAB的命令行窗口对该函数进行调用,语句为[ex,Nxdt]=OrSy TFA(54000,18000,0.25,8800,1050,1050,28,140,42,0.2),执行完该语句可得到本例的计算结果为:拉伸极限载荷(Nx/t)u=198.33 MPa,极限应变ε0x=0.019 06,与文献[6]的结果基本吻合,存在微小差别的原因在于文献[6]采用的是Hill-Tsai强度准则,而本文考虑了单层板拉、压强度的不同,采用了Tsai-Wu强度准则。
图4 为拉伸极限载荷随正交铺设比的变化规律。从图中可以看出,极限载荷Nx/t随m的增大而增大,这是因为x方向为0°层的纵向,但对90°层却是横向,则0°层x方向的承载能力远大于90°层,m增大即为0°层的比例增加,因此Nx/t也随之增加。
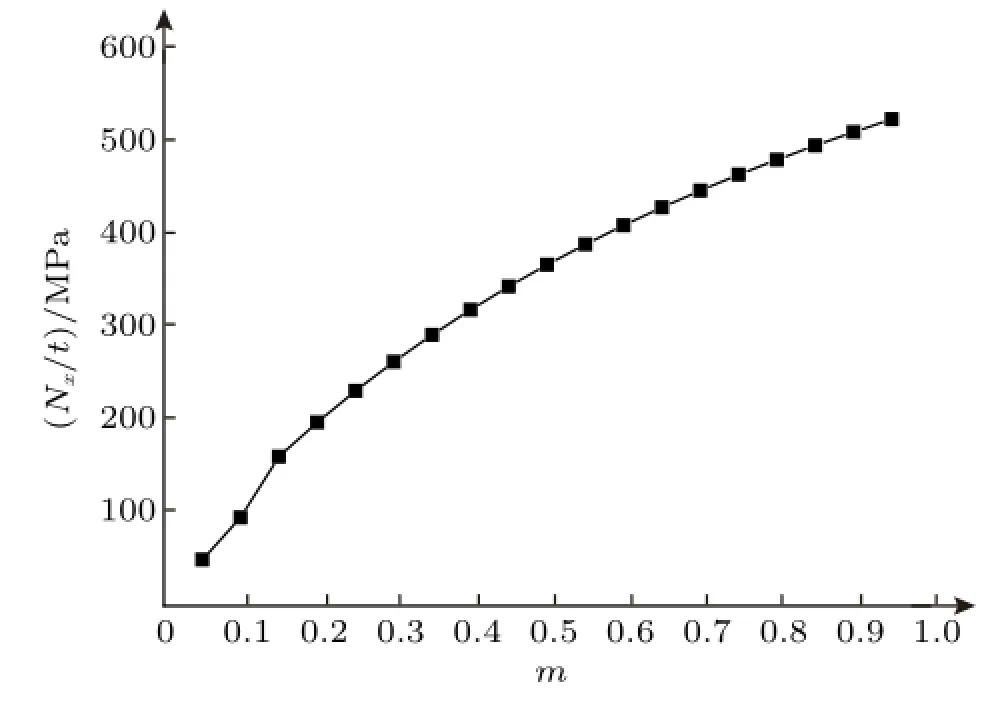
图4 拉伸极限载荷随正交铺设比的变化规律
但不难发现,当m从0.1增加到0.15时,Nx/t增幅突然提高,随后逐渐减小,这是为什么呢?可以通过在“fail.dat”文件中分析层合板的破坏过程寻找答案。图5显示了m分别为0.05,0.1和0.15时层合板的破坏过程。从中可以看出:当m≤0.1时,90°层的破坏随之引起0°层y方向的连锁破坏,但0°层在x方向还可以继续承载,需要用增量法进行第二次计算,层合板经历两次加载过程即发生破坏;但当m>0.1时,90°层的破坏不会引起0°层的连锁破坏,层合板的破坏经历三次加载过程才最终破坏。由此可见,当单层破坏时,检验有无其他层发生连锁破坏这一步是十分必要的。
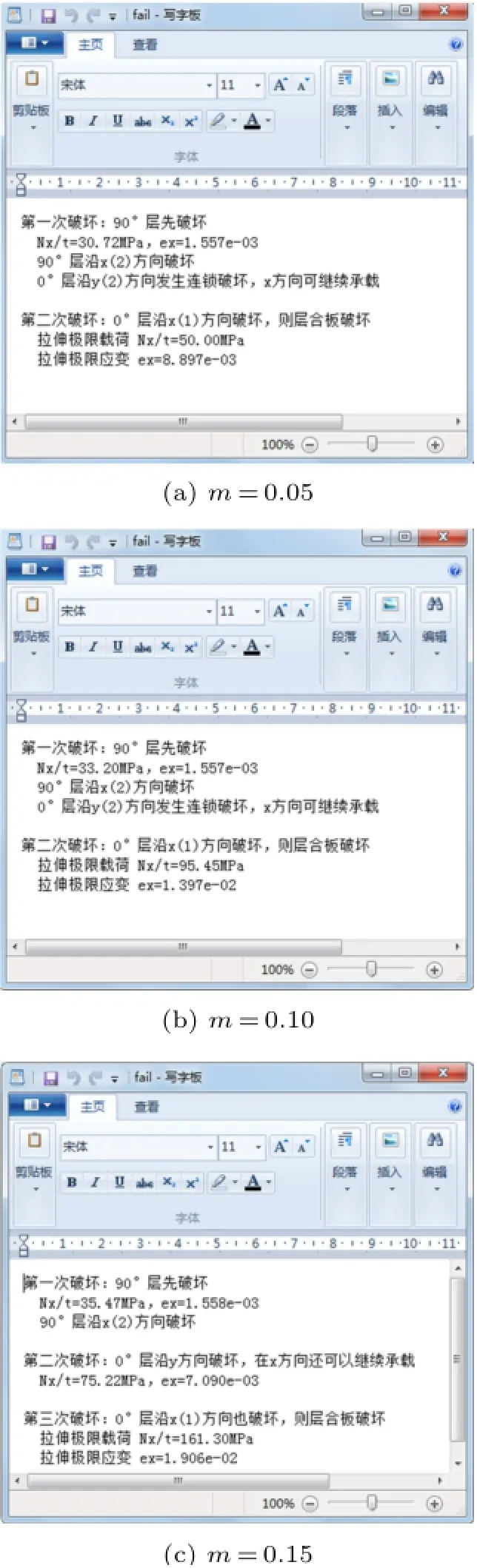
图5 层合板破坏过程的记录文件
4 结论
本文以复合材料力学课程中的难点--层合板的强度分析为例,提出一种将MATLAB编程引入复合材料力学课程中的方法。相比传统教学中繁琐的公式计算和推导相比,该方法的优点在于:(1)化繁为简,提高计算效率。层合板的强度分析往往需要多步计算才能最终得到极限载荷,计算工作量庞大。但事实上,每步计算都包含许多重复的部分,如:单层板的应力计算、单层破坏载荷的计算等。利用MATLAB编程,既可将这些需重复计算的部分编制为子函数进行调用,使程序更简洁,还可解决许多复杂的数学计算问题,使得分析过程大为简化。(2)便于对该问题进行参数化讨论。采用参数化编程,不只局限于对一种参数下的层合板进行强度分析,还可研究层合板的强度及破坏规律随某些参数的变化规律,为层合板的设计提供可靠的理论依据。
