一种“有无穷远虚铰的三刚片规则”的证明方法1)

刘亚菲 舒开鸥 郭子涛 张雷

(九江学院建筑工程与规划学院，江西九江332005)

三刚片规则是平面体系几何组成分析的核心方法，对于规则中含有无穷远虚铰(连接两刚片的两平行链杆)的情形，往往是教学难点，由于现行教材[1-2]中均没有对这一情形详细易懂的证明，影响了学生对知识的理解。相关文献[3-4]虽给出了证明方法，但采用的是本科阶段并未涉及的射影几何知识，无助教学应用。

本文应用理论力学[5]中刚体平面运动学知识，分析了虚铰和无穷远虚铰的运动学特性，提出了两个运动学定理，在此基础上结合其他运动学基本理论，针对有无穷远虚铰的三刚片规则，给出了详细且简明的证明，方便了学生更好理解这一规则，也开拓了平面体系几何组成分析的新思路。

1 两个定理及其证明

1.1 定理一：两刚片(或其扩展部分)在虚铰处速度

相等

证明：设刚片I和刚片II的角速度矢分别为ω1和ω2，它们在O点(两刚片上或刚片的扩展部分上与虚铰位置重合的点)的速度矢分别为vO1和vO2，杆AC和杆BD的角速度矢分别为ωAC和ωBD，并设矢量AC=aOA，BD=bOB，如图1。

对刚片I和刚片II，分别以O点为基点，有

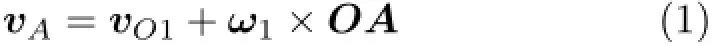
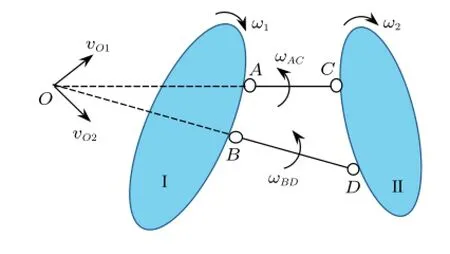
图1

对杆AC和杆BD，分别以A点和B点为基点，结合式(1)和式(2)有

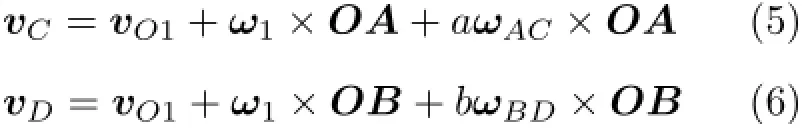
式(5)减去式(3)，式(6)减去式(4)，得

注意到杆AC和杆BD不平行，即OA和OB不平行，若要式(7)成立，必有

此时可得：vO1=vO2，于是“两刚片(或其扩展部分)在虚铰处速度相等”成立。

1.2 定理二：无穷远虚铰(两根平行链杆)连接的两刚片，角速度相等

证明：设刚片I的速度瞬心为O点，刚片I和刚片II角速度矢分别为ω1和ω2，两平行链杆AC和BD的角速度矢分别为ωAC和ωBD，如图2。对杆AC和BD，分别以A点和B点为基点，有对刚片II，以D点为基点，结合式(9)有

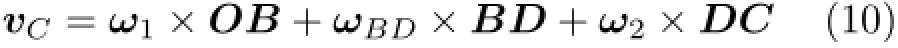
式(10)减去式(8)，并将BA=OA-OB和DC=BA+AC-BD代入，得

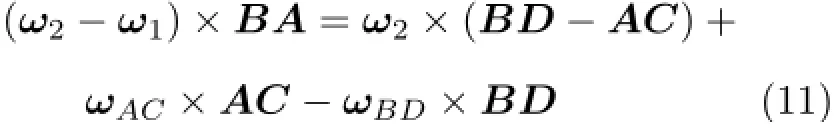
式(11)等号左侧的结果矢量在平面内垂直BA；由于杆AC和杆BD平行，故等号右侧的结果矢量在平面内垂直AC或BD，又由于BA不可能与AC或BD平行，若要式(11)成立，必有等号两边都为0，得：ω2=ω1，于是“无穷远虚铰(两根平行链杆)连接的两刚片，角速度相等”成立。

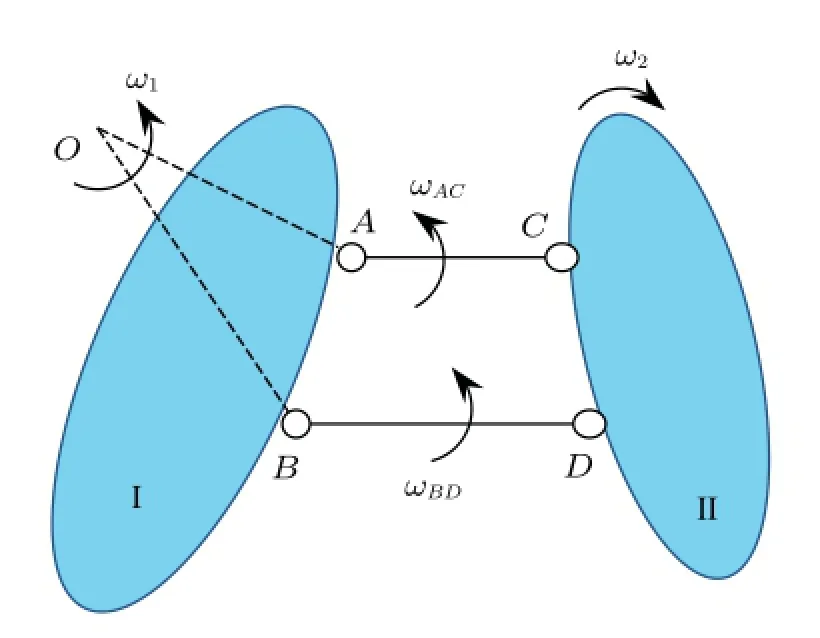
图2

2 有无穷远虚铰的三刚片规则的证明

2.1 有一个无穷远虚铰的情形

三刚片规则中，若有一个无穷远虚铰，且它不与另两铰的连线平行，规则仍然成立，即体系是无多余约束的几何不变体系，如图3。

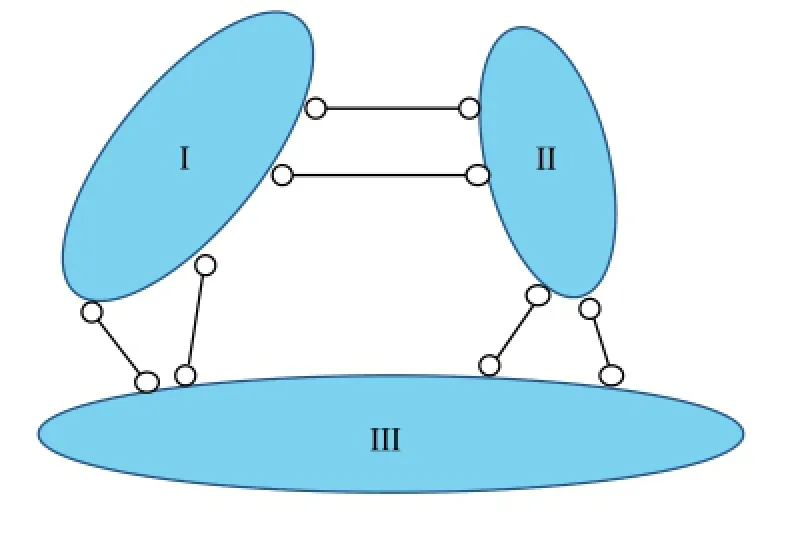
图3

证明：固定刚片III，由定理一可知刚片I在虚铰A处及刚片II在虚铰B处的速度必均为零，因此若刚片I和刚片II能动，则只能分别绕A和B转动，又因为用无穷远虚铰连接，由定理二可知刚片I和刚片II的角速度相等，设为ω，如图4。设A和B到链杆CD的距离分别为a和b，不难得出C和D两点的速度在链杆CD上的投影分别为：vCD=ω·a，vDC=ω·b。在链杆CD上根据速度投影定理，得

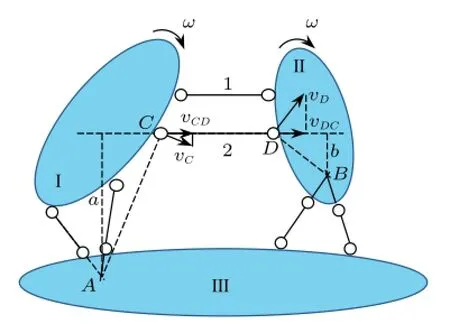
图4

考虑到链杆CD与两虚铰A和B的连线不平行，即a/=b，若要式(12)成立，只能有ω=0，这表明刚片I和刚片II均只能固定不动，即体系几何不变。

2.2 有两个无穷远虚铰的情形

三刚片规则中，若有两个无穷远虚铰，且它们不平行，规则仍然成立，即体系是无多余约束的几何不变体系，如图5。

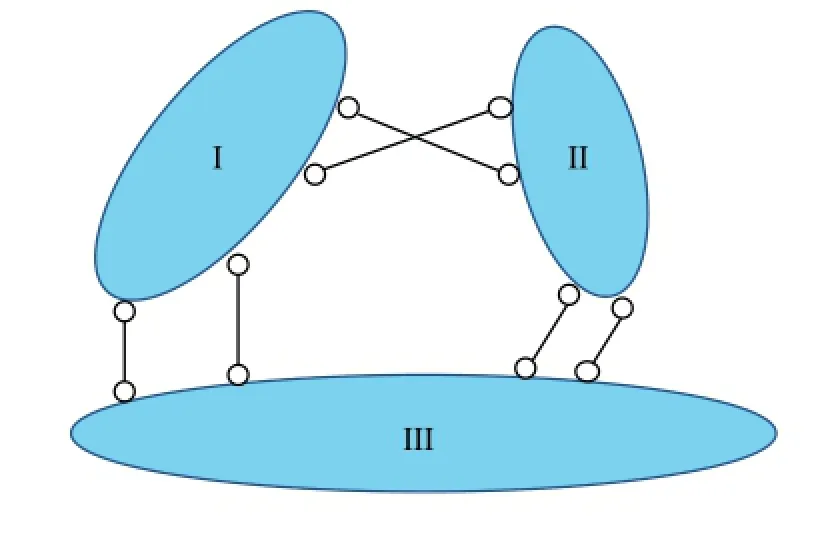
图5

证明：固定刚片III，由于与刚片III均由无穷远虚铰连接，由定理二可知若刚片I和刚片II能动，则只能分别沿垂直无穷远虚铰方向平动，设它们的速度矢分别为v1和v2，如图6。因为两无穷远虚铰不平行，故必有v1/=v2，刚片I和刚片II由虚铰A连接，由定理一知它们在虚铰A处的速度相等，即v1=v2，于是只能有v1=v2=0，这也表明刚片I和刚片II只能固定不动，即体系几何不变。

图6

2.3 有三个无穷远虚铰的情形

三刚片规则中，若连接三刚片的三个铰均为无穷远虚铰，则体系是几何可变体系，如图7。

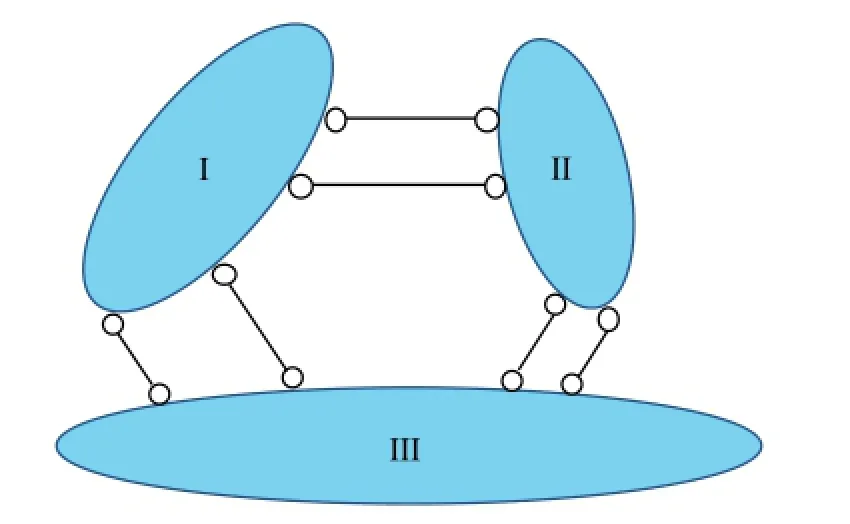
图7

证明：固定刚片III，由于与刚片III均由无穷远虚铰连接，由定理二可知若刚片I和刚片II能动，仍只能分别沿垂直无穷远虚铰方向平动(即两刚片角速度均为0，自然满足定理二)，设速度分别为v1和v2，如图8。此时只要v1和v2沿连接刚片I和刚片II的无穷远虚铰方向上的分量相等，即满足速度投影定理，于是v1和v2可不必都为0，这表明刚片I和刚片II至少有一个可动，即体系几何可变。

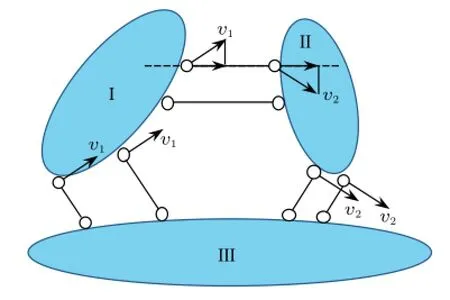
图8

3 结语

本文利用理论力学中刚体平面运动学知识，解决了结构力学中有无穷远虚铰的三刚片规则的证明问题，不仅使结构力学知识更易于理解、掌握，也直观体现了理论力学基础知识在力学学习中的意义与价值，还为力学教学中各课程的交叉融合提供了很好示范。

以本文对有无穷远虚铰的三刚片规则的证明为启发，在平面体系尤其是复杂体系(不能用两刚片规则或三刚片规则等基本方法分析的体系)的几何组成分析中，可尝试建立基于刚体平面运动学基本理论的新的分析方法。以图9的复杂体系为例[6]，简要说明这一分析方法。

图9

体系中A、B和C三点是固定不动的，若体系可变(即可动)，则杆AD、BD和CG只能分别绕点A、B和C转动，假设D点速度vD向下，则点E和F速度vE和vF均向下，如图10。在杆EG上利用速度投影定理，可知点G速度vG向右，再在杆FG上利用速度投影定理，得根据式(13)不难得到vD和vE均为0，于是各结点均固定不动，即体系几何不变，求出体系的计算自由度为0，所以该体系为无多余约束的几何不变体系。

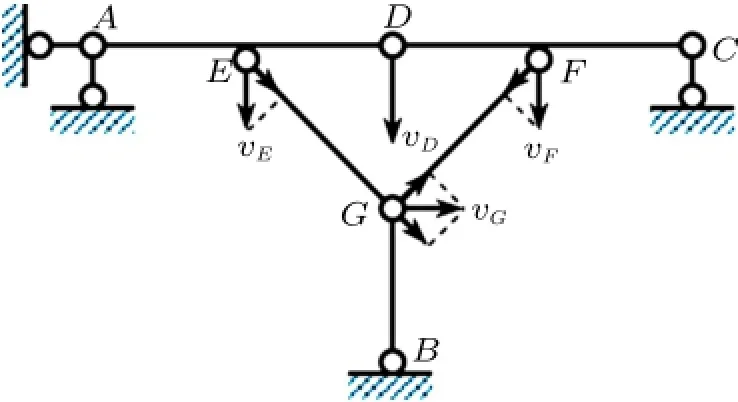
图10