复杂载荷作用下梁的弯曲变形微分求积法求解1)
2021-01-06葛仁余吕良伟朱浩杰聂子龙张金轮
葛仁余 吕良伟 朱浩杰 聂子龙 张金轮
(安徽工程大学建筑工程学院,安徽芜湖241000)
材料力学中求平面弯曲梁的挠度和转角采用的基本方法是弯矩方程积分法,即首先建立挠曲线近似微分方程,进行二次积分运算再结合边界条件获得挠度方程和转角方程。但是弯矩方程积分法分析梁的弯曲变形时,需要事先获得梁上任意位置的弯矩方程,当梁上作用任意分布载荷时确定梁的弯矩方程十分困难[1-3]。另一方法是载荷方程积分法[4],需要进行四次积分运算结合边界条件才能得到挠度方程。当任意分布载荷为简单的线性表达式时,由载荷方程积分法可以获得弯曲变形的精确解,但是,当分布载荷为非线性表达式时,载荷方程积分法运算过程将会繁琐冗长。积分法是计算弯曲变形的基本方法,其优越性在于可用解析方法得到挠度方程和转角方程,但是,当梁上作用较多外载荷时,需要分段建立弯矩积分方程和载荷积分方程,而在分段积分时,积分常数的个数分别是分段数的两倍或四倍,因此,用积分法求解复杂载荷的变形问题时,耗费在积分运算和积分常数确定方面的工作量很大,也容易出错,使得积分法在工程实际计算中的应用受到较大的限制。
正是弯矩方程积分法或载荷方程积分法在工程实际计算中受到较大的限制,本文引入微分求积法[5]求解任意复杂载荷下梁的弯曲变形问题。首先,根据叠加原理将作用在梁上的复杂载荷分解为各个单独载荷,再由微分求积法将各个单独载荷作用在梁上的载荷方程边值问题转化为求解线性代数方程组问题,通过Fortran语言编制通用程序计算,从而获得梁的挠度和转角的数值解,最后,将计算结果累计叠加,从而获得多个载荷作用下梁的挠度和转角。该法使梁的弯曲变形计算得以程序化,可避免弯矩方程积分法和载荷方程积分法中确定积分常数时一系列繁琐的代数运算,尤其对于积分方法求解区间分段数较多的梁弯曲变形计算非常适用,因此,本法在求解梁的弯曲变形教学中具有巨大的功效。
1 梁的载荷方程及微分求积法原理
1.1 单个载荷作用下梁的载荷方程
如图1所示,梁长为L,抗弯刚度为EI,q0为常数。图1(a)有作用在梁上的任意分布载荷q(x)=q0f(x),图1(b)有作用在梁上的集中载荷F=q0L,图1(c)有作用在梁上的集中力偶Me=q0L2。以变形前的梁轴线为x轴,垂直向上的轴为y轴,变形后梁的轴线将成为xy平面内的一条曲线,称为挠曲线,挠曲线上横坐标为x的任意点的纵坐标称为挠度,记为y=y(x);变形中梁的横截面对其原来的位置转过的角度θ,称为转角,记为θ=y′(x),在图1所示的坐标系中,向上的挠度和逆时针方向的转
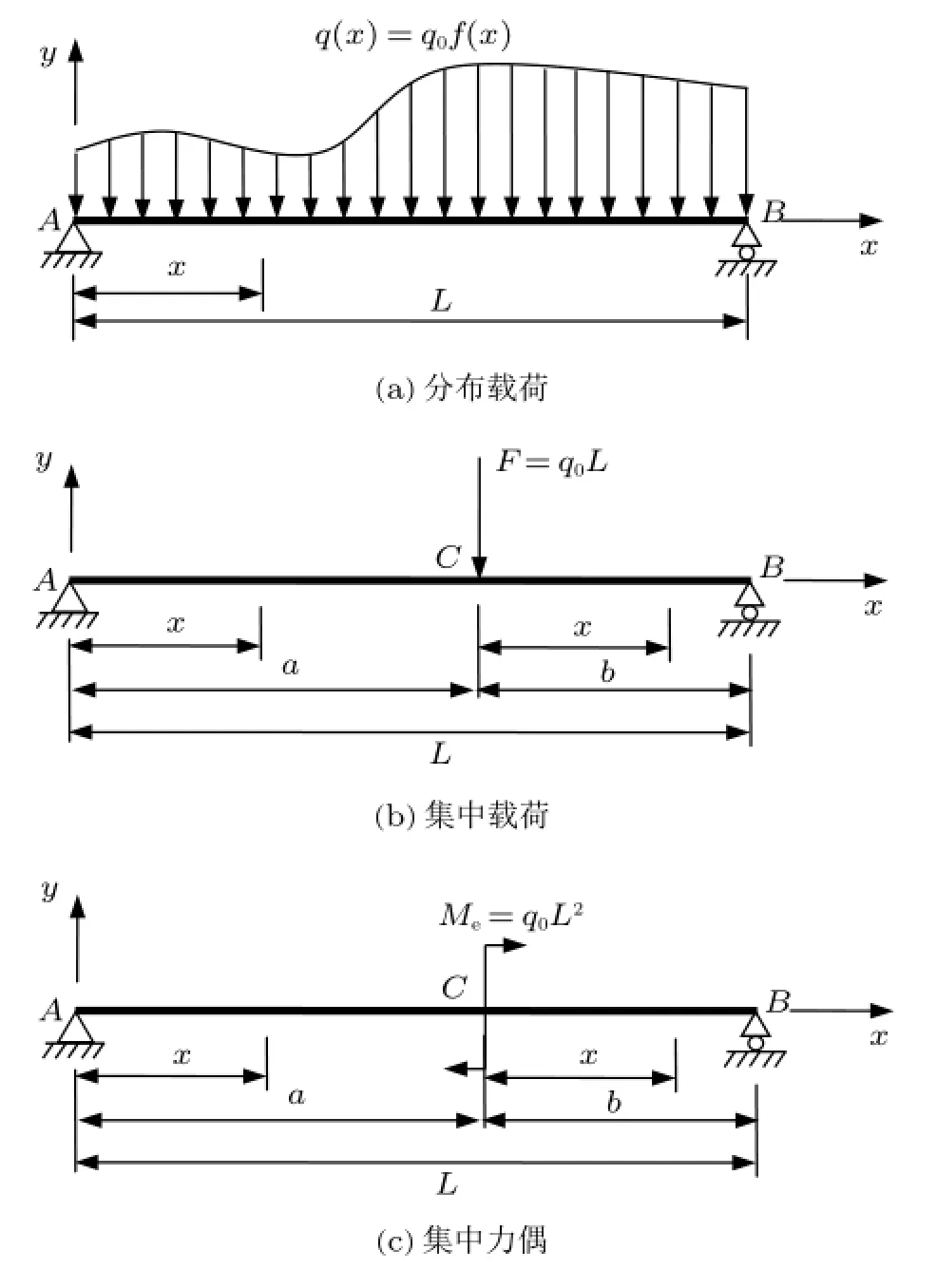
图1 单个载荷作用下的简支梁
角为正,反之为负。根据文献[4],图1(a)梁的载荷方程为
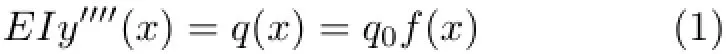
为了便于编程计算,引入无量纲变量ξ=x/L,ξ∈[0,1],将其代入式(1)可得
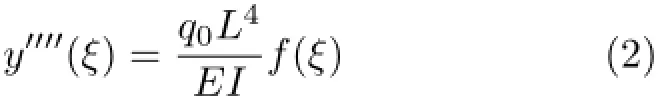

图1 (a)简支梁两端的边界条件为因此,图1(a)任意分布载荷下的梁的弯曲变形问题,就是在边界条件式(3)下,求解微分方程式(2)的边值问题。同理,根据文献[4],图1(b)和图1(c)梁中,设AC梁段的挠度为yI(x),引入无量纲坐标ξ=x/a,x∈[0,a],ξ∈[0,1],梁的载荷方程为

设CB梁段的挠度为yII(x),引入无量纲坐标ξ=x/b,x∈[0,b],ξ∈[0,1],梁的载荷方程为

图1 (b)和图1(c)简支梁两端的边界条件为
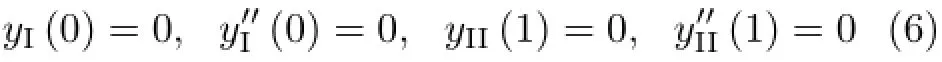
图1 (b)和图1(c)简支梁在C处的交界条件为
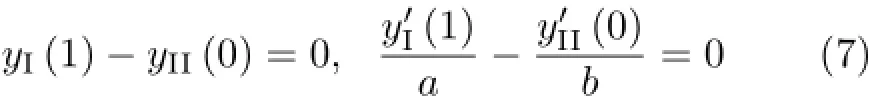
在集中载荷作用下有
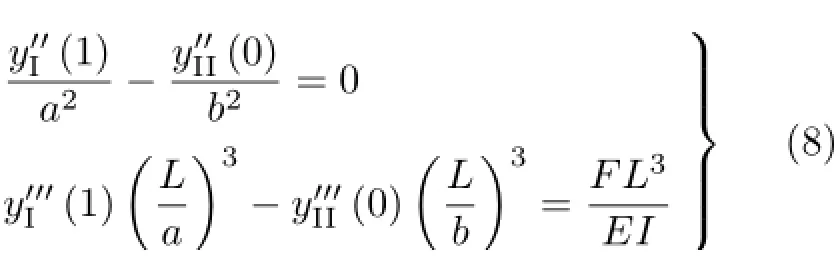
在集中力偶作用下有
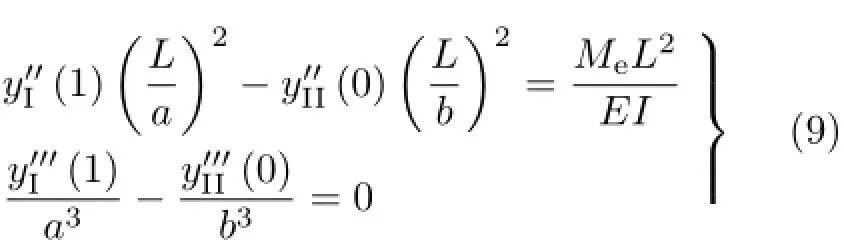
因此,图1(b)集中载荷作用下的梁的弯曲变形问题,就是在边界和交界条件式(6)~式(8)下,求解微分方程式(4)和式(5)的边值问题。图1(c)集中力偶作用下的梁的弯曲变形问题,就是在边界和交界条件式(6)、式(7)和式(9)下,求解微分方程式(4)和式(5)的边值问题。
至此,根据叠加法原理,任意多个载荷共同作用下的梁的弯曲变形,可由单个分布载荷q(x)=q0f(x)、集中载荷F=q0L和集中力偶Me=q0L2单独作用在梁上变形的叠加而获解。
1.2 微分求积法计算梁的载荷方程
微分求积法是Bellman等[5]于1971年提出的基本理论,该方法求解微分方程具有公式简单、编程方便、计算量少和精度高等优点。不失一般性,以1.1节图1(a)单个分布载荷作用下梁的变形为例,将梁长区间ξ∈[0,1]均匀等分为n段n+1个节点ξi,ξ0=0,ξn=1表示的近似值(i=0,1,···,n)。
将微分方程式(2)中待求函数y(ξ)用节点函数值进行拉格朗日插值来描述,即
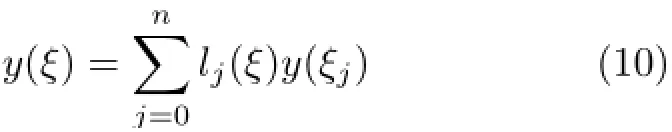
式中lj(ξ)为拉格朗日插值基函数。将式(10)求导,得
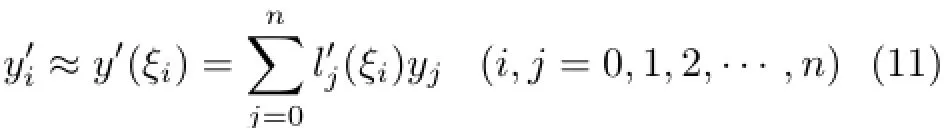
式(11)写成向量和矩阵形式,得

这里,
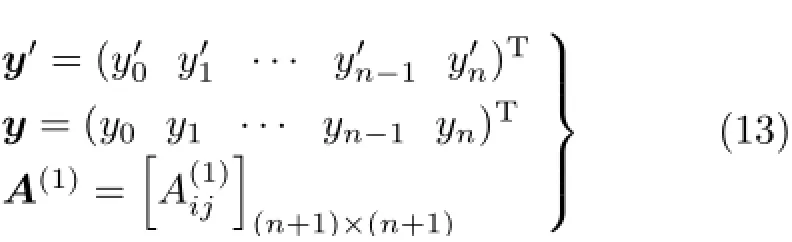
A(1)称为权系数矩阵,矩阵元素高阶导数顺次地采用低阶导替换,逐步递推可得
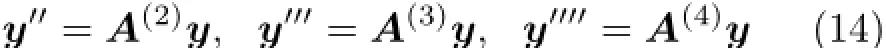
其中,

令q0L4/(EI)=1,以下同。将式(14)代入式(2),写成向量和矩阵形式,得

其中,f=(f(ξ0)f(ξ1)···f(ξn-1)f(ξn))T。
不失一般性,以图1(a)简支梁为例,设I为(n+1)×(n+1)阶单位阵,将边值条件式(3)写成向量形式
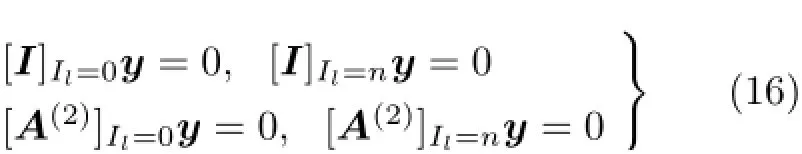

行、第n行置换,得新向量则有这里,采用Fortran语言编制通用程序计算,由高斯主元消去法求解式(17)线性代数方程组获得未知量y。同理,1.1节的图1(b)集中载荷和图1(c)集中力偶分别作用下梁的弯曲变形也可类似用微分求积法编制程序获解。
2 教学实例分析
为了验证本文微分求积法程序化求解受复杂载荷作用的梁弯曲变形的可行性和精确性,本文通过3个教学实例进行分析。设梁长为L,抗弯刚度EI为常量,分布载荷为q(x),集中载荷为F=q0L,集中力偶为Me=q0L2(q0为常数),在以上三种载荷共同作用下,由微分求积法求解梁的挠度和转角。
2.1 教学实例一
如图2所示,在课堂教学中,为了验证微分求积法分析梁弯曲变形问题的精确性,我们使用Fortran语言编制通用程序计算,用数值计算方法代替繁杂的载荷方程积分法。按等步长方式布置离散节点,在梁长区间AC段和CB段上,皆取离散单元数为n=16,节点数为n+1=17,计算结果如表1所示,由表1可知,微分求积法计算简支梁中点挠度yC、两端转角θA和θB结果与文献[4]精确解完全吻合,充分说明了微分求积法在教学中计算受弯梁挠度和转角的可行性和精确性。
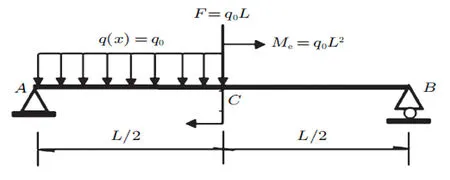
图2 教学实例一简支梁外载荷示意图
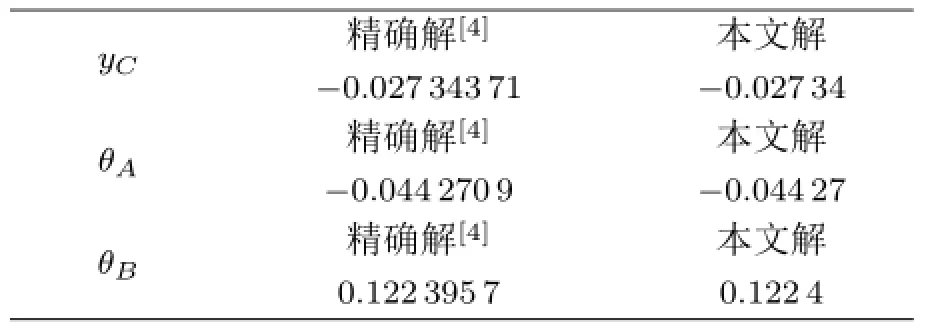
表1 简支梁弯曲变形的数值解与精确解对比
图3~图4 是图2简支梁在复杂载荷作用下的挠度和转角微分求积法计算值与精确解的对比,计算结果表明:微分求积法获得梁的挠度曲线y(x)和转角曲线θ(x)的数值计算结果与文献[4]精确解曲线完全重合,再次验证了本文微分求积法计算复杂载荷作用下受弯梁挠度和转角的精确性。
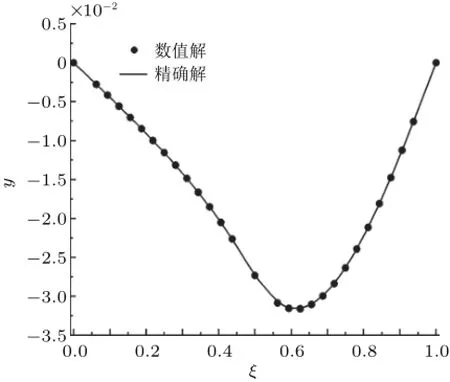
图3 教学实例一:简支梁的挠度曲线
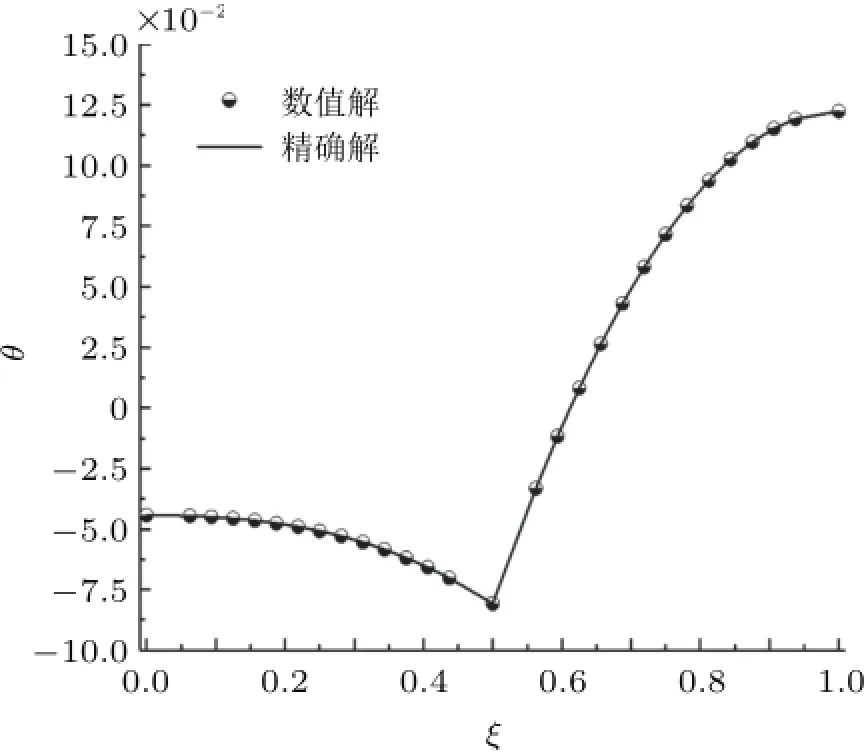
图4 教学实例一:简支梁的转角曲线
2.2 教学实例二
如图5所示,由于作用在梁上的分布载荷q(x)=q0cos[sin(x/L)]为非线性表达式,课堂教学中运用载荷方程积分法求解,耗费在积分运算和积分常数确定方面的工作量很大。若采用微分求积法编制通用程序计算,则可避免人工积分法运算过程的繁琐冗长问题。同时,为了验证微分求积法的收敛性,在AC段和CB段区间取离散单元数分别为n=8,12,16和20,按等步长方式布置离散节点,由微分求积法获得图6和图7计算结果。由图6和图7可知:当n=8时计算值误差较n=12时大,随着区间离散单元数n的增加,梁的挠度和转角加速收敛,当n≥16时,梁的挠度曲线和转角曲线完全收敛。

图5 教学实例二:简支梁外载荷示意图
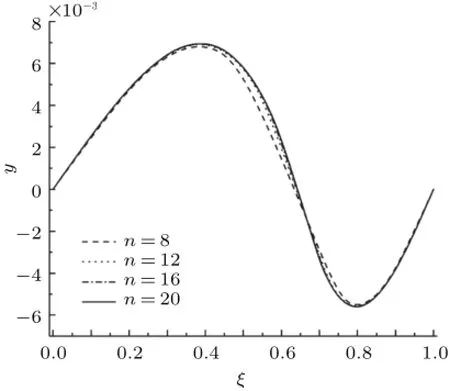
图6 教学实例二:简支梁的挠度曲线
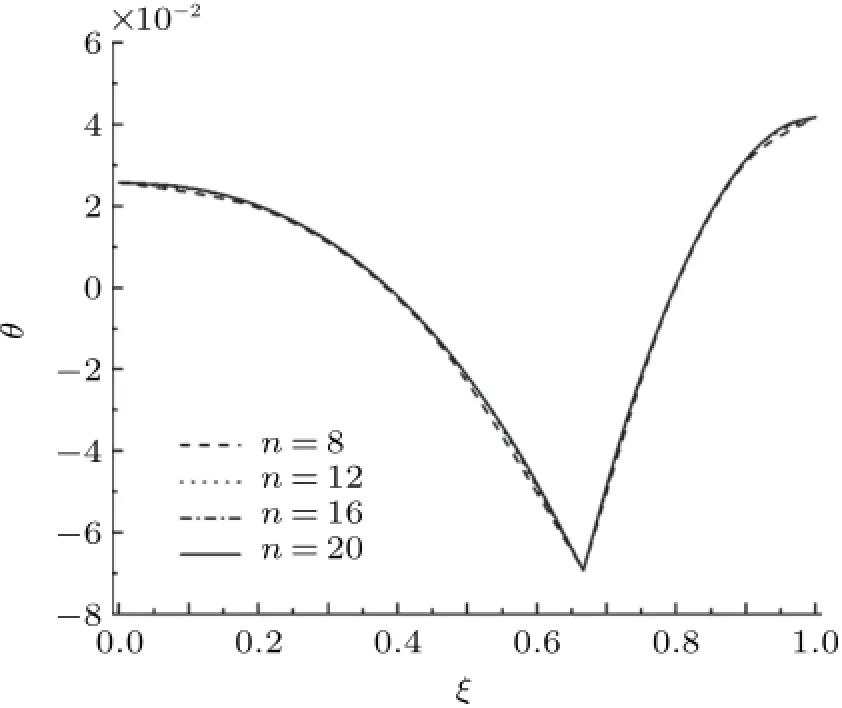
图7 教学实例二:简支梁的转角曲线
2.3 教学实例三
算例2.1和2.2简支梁的区间分段数为2段,为了验证微分求积法可以求解更多的区间分段数,算例2.3的简支梁求解区间分段数为3段,如图8所示。在梁长区间AC段、CD段和DB段上,皆取离散单元数为n=16,节点数为n+1=17,按等步长方式布置离散节点,由微分求积法获得梁的挠度曲线y(x)和转角曲线θ(x),分别如图9和图10所示,与文献[4]精确解曲线完全重合。
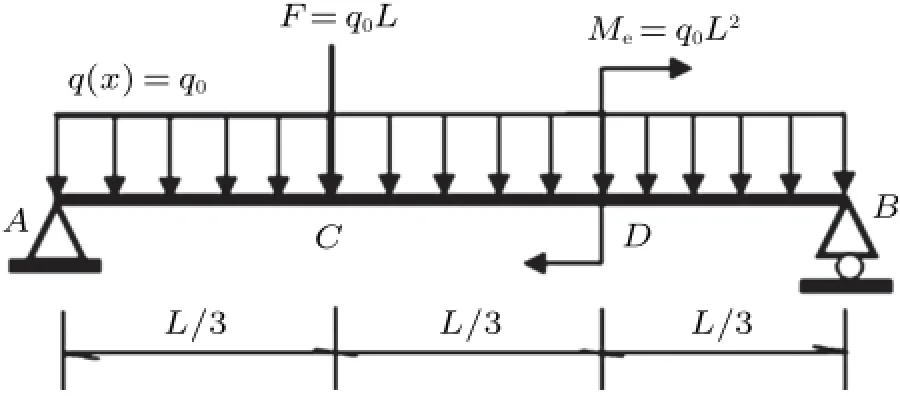
图8 教学实例三:简支梁外载荷示意图
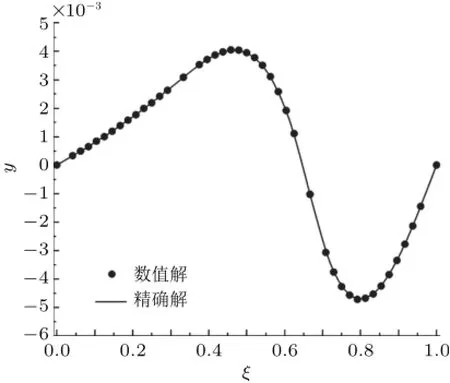
图9 教学实例三:简支梁的挠度曲线
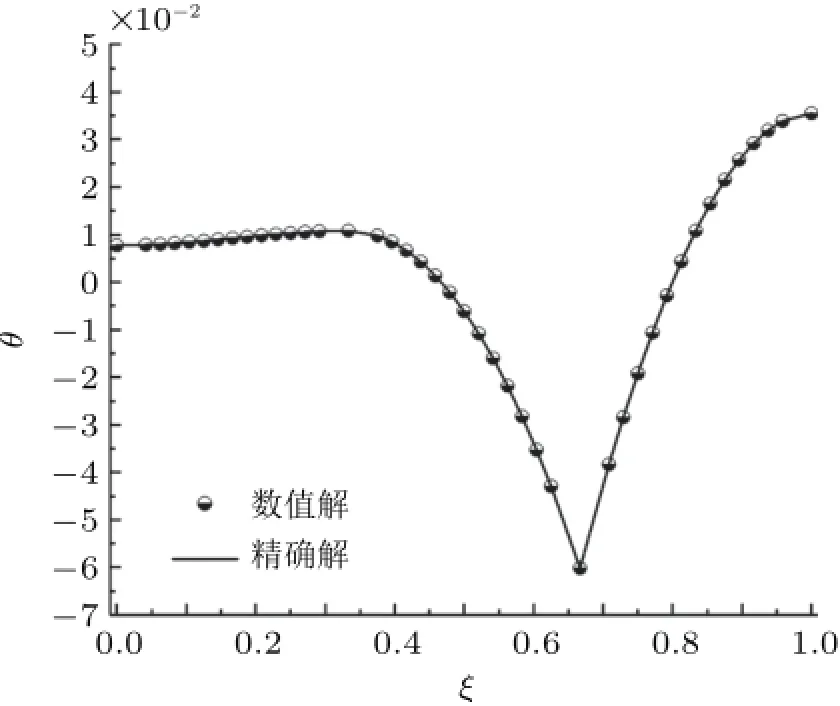
图10 教学实例三:简支梁的转角曲线
3 结语
(1)当梁上作用较多复杂载荷时,需要分段建立载荷方程,积分运算过程繁琐冗长,尤其分布载荷为非线性表达式时,人工积分法运算过程十分繁琐。采用微分求积法编制通用程序计算,无论分布载荷为线性表达式还是非线性表达式,梁的分段数有多么多,受弯梁的挠度和转角皆可顺利获解。文中教学实例2.1和教学实例2.3给出了数值解与精确解完全吻合的计算结果,验证了微分求积法在弯曲变形计算中的可行性和精确性。
(2)在弯曲变形课堂教学中,当载荷方程积分法求解梁的弯曲变形问题受到限制时,我们可以借助Fortran语言编程计算获得数值解,这一教学过程既让学生体会到求解方法的多样性,提高学生的学习积极性和兴趣,也让学生们掌握编制程序解决力学问题的一技之长,对他们今后的学习与工作都有较大帮助。
