理论力学教具DIY系列(三)悬崖勒马玩具的原理及分析

高云峰

(清华大学航天航空学院，北京100084)

我曾经为学生设计过一个“悬崖勒马”的探究项目：小马身上连一根绳子，加上配重后，可以让小马走到悬崖边上(桌面边界当悬崖，图1)。让学生探究配重与小马的运动学和动力学关系，即如何让小马不落下悬崖但是又尽可能走得远？

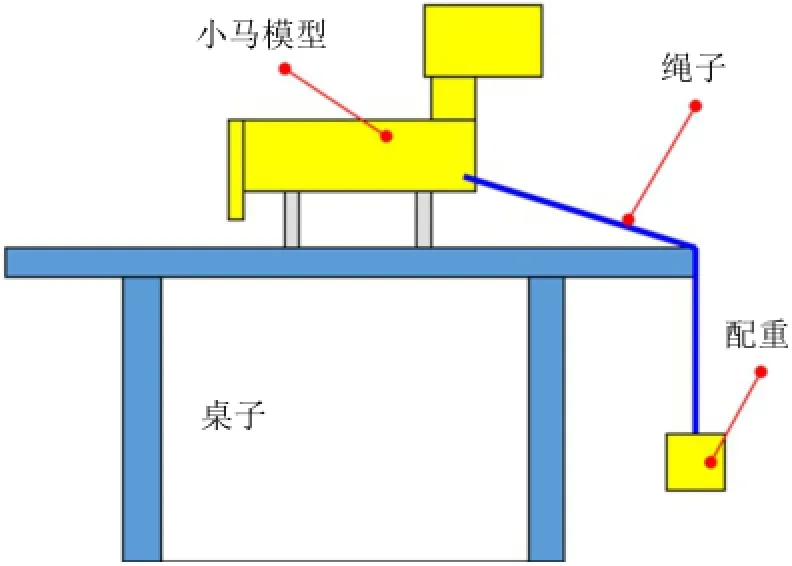
图1 探究活动

后来中央电视台导演到我实验室参观，对我设计的一些科学游戏(包括悬崖勒马)很感兴趣，后面就合作变成了《加油！向未来》节目中的大型游戏。节目中把小马改为小车，人坐在其中。把人和小车作为一个整体，配重暂不考虑尺寸大小。即使这样简化后，装置的运动也是很复杂的，原因是它的自由度在1～5之间变化。

1 第一阶段建模

这一阶段小车完全在台面上运动，系统有一个自由度：小车质心位移x。装置的模型见图2，参数如下：小车长为a，高为b，质量为m1；质心距离前端为a1，距离底部为b1；系绳处距离底部为h；配重质量为m2；绳长为l，不计质量且不可伸长；台面长为L，摩擦系数为μ1。装置各部分受力图见图3，这一阶段绳子拉动小车运动，绳子与台面角度为θ，边缘A点考虑为一段微小圆弧(只影响绳子与接触面的张角，不影响水平位移)，摩擦系数为μ2，绳子与圆弧的张角为π/2-θ。

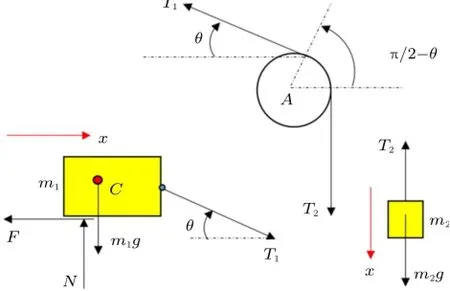
图3 第一阶段受力图

根据各部分的受力情况，可以列出动力学方程及补充条件为

其中tanθ=h/(L-x-a1)。

方程(1)是微分-代数方程，在数值计算中，可以先把¨x当作代数量，求出¨x后再求微分方程(在下一篇中详细介绍)。在方程(1)中令¨x＞0，可以得到小车从静止到运动的临界质量比为

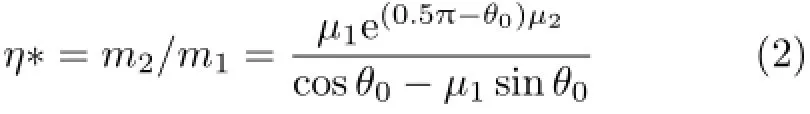
其中tanθ0=h/(L-a1)。

方程(1)适用的范围是x+a1≤L(即小车前缘没有冲出边界)，一旦小车冲出边界，绳子就会摆动起来，受力图和方程都要改写了，进入第二阶段。

2 第二阶段建模

第二阶段受力图如图4所示。当小车前缘超出了桌面平动时，系统有二个自由度：小车质心位移x、绳子摆角β。绳子摆动时可以考虑空气阻尼(如果小车停止在平台上，绳子长时间摆动)。

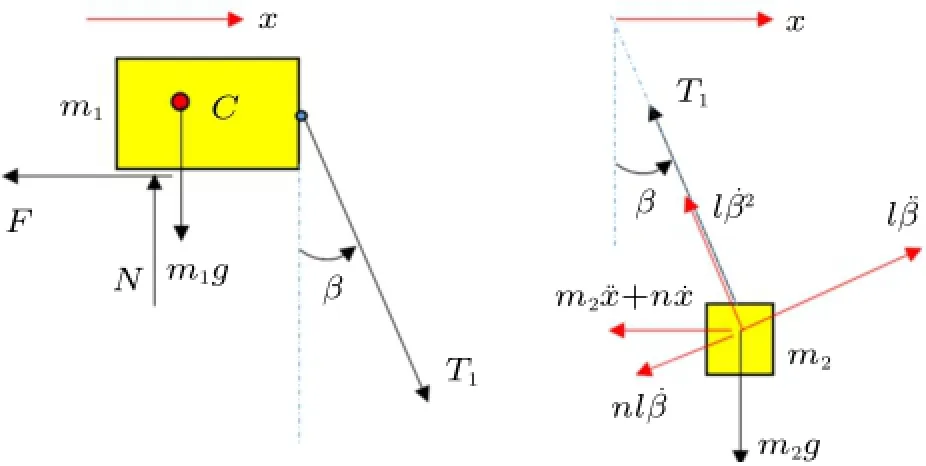
图4 第二阶段受力图

小车的动力学方程直接可以列出，但要注意配重的悬挂点在运动，可以采用非惯性系中的处理方法，加上牵连惯性力后再列相对运动微分方程，得到如下方程

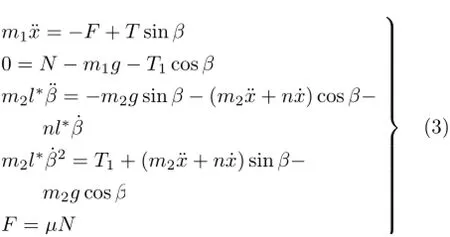
其中l*=l，β≥0;l*=l-h，β＜0。方程(3)的终止条件是：小车出现绕A点的转动，具体为

该条件一旦满足(已经不安全了)，进行第三阶段。

3 第三阶段建模

第三阶段受力图如图5所示。当小车超出桌面较多时且产生转动时，系统有三个自由度：小车质心位置x和y、转角α、绳子摆角β，但是由于小车与台面接触还有一个约束方程

图5 第三阶段受力图

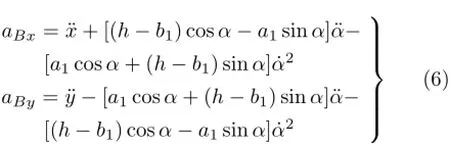
这时要注意绳子端点B的加速度为不考虑空气阻尼，从而得到系统的动力学方程为

其中f(α，β，F，N，T1)是已知函数。方程(7)要与约束方程(5)和方程(6)联立才能求解。在求解过程中，一旦满足N=0或小车尾部超出平台边缘，表示小车脱离台面，进入下一阶段。

4 第四阶段建模

第四阶段受力图如图6所示。当小车脱离桌面且绳子绷紧时，系统有自由度：小车质心位置x和y、转角α、绳子摆角β。B点的加速度仍是式(6)。

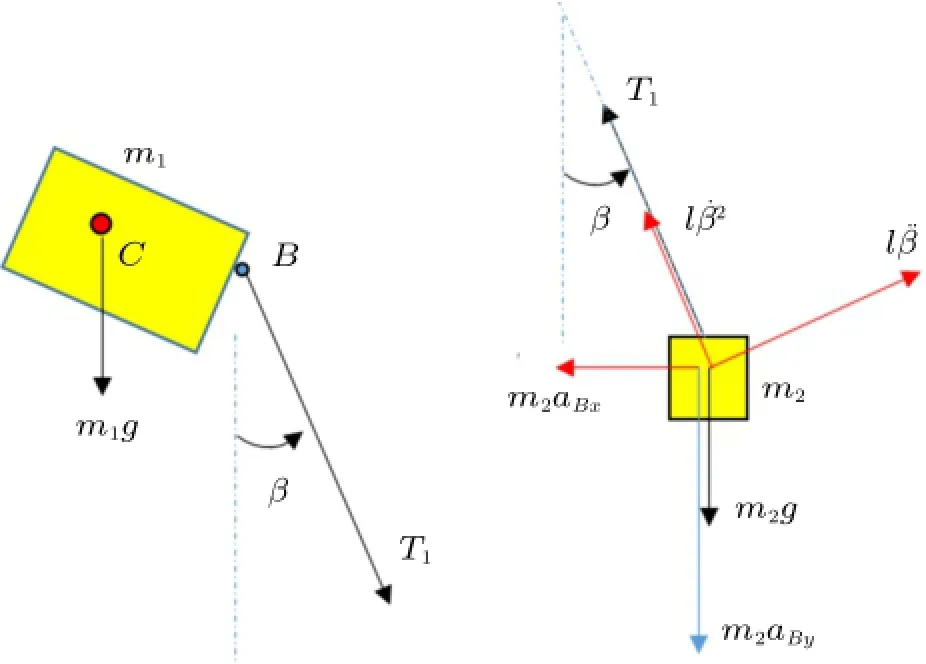
图6 第四阶段受力图

从而得到系统的动力学方程为

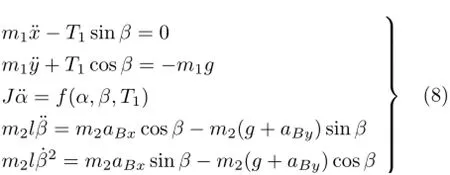
其中f(α，β，T1)是已知函数。在求解过程中，一旦满足T1≤0，就表示小车与配置之间的绳子松弛了，进入下一阶段。

5 第五阶段建模

当小车与配重之间绳子未绷紧时，是五自由度问题：小车质心位置x和y、转角α、配重质心位置x2和y2。不过动力学方程却很简单，有

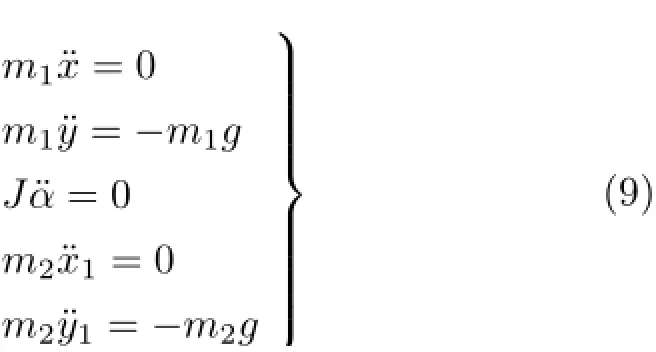
6 部分计算结果及结论

在一定的配重下，小车前部可以冲出台面边缘而最终停住，其原理是：绳子的拉力是小车前进的动力，而摩擦力是小车刹车的原因。关键是：绳子拉力的水平分量随小车前进而减少，而摩擦力分量随小车前进而增加。

对于载人游戏，安全是第一位的，所以首先要确定配重的范围，即

小车质量比与最终位移关系如图7所示，从图中可以看出，配重与小车的临界质量比为η*=m2/m1=27.43%(具体可由式(2)得到)，η＜η*时小车不能运动，η＞η*时小车才能运动起来。η=29.60%时小车前缘已经到了台面的边界(但是安全)，η＞35%时小车整体冲出台面边界(危险)。从表演的角度，质量比η≈34%时最刺激：前缘能冲出台面，配重摆动起来，小车最终安全停留在台面上，根据方程(3)和方程(4)，令加速度为零及y=b1，β=0，该情况下小车前缘最多可以伸出边界a1m1/(m1+m2)≈0.6 m，当然实际上要保守一点。

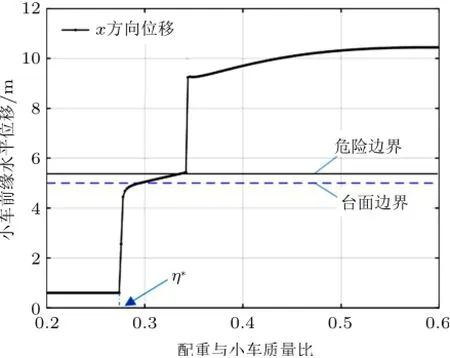
图7 质量比与最终位移关系

但是图7有一个疑问，如果η比η*稍大一点，小车为什么会先运动然后停在台面上？图8是不同质量比情况下小车的速度与位移关系，可以看到：不同质量比情况下小车均是先加速再减速，其中牵引小车的绳子角度是关键：开始时θ小，拉力T1的水平分量大，小车加速；当小车向前运动使θ变大后，一方面拉力T1的水平分量变小，另一方面压力分量增加使摩擦力增加，导致小车减速。如果小车速度降到0之前就到了危险边界(L+a1m1/(m1+m2)=5.6 m)，则会冲出台面。

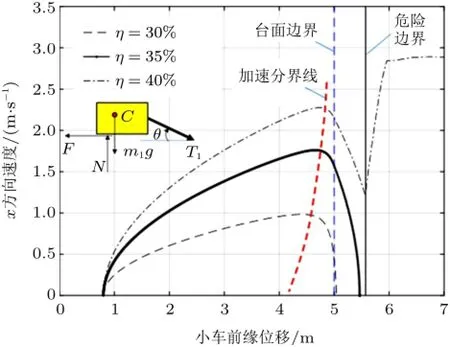
图8 不同质量比的位移与速度关系

另一个问题是，图7中的曲线为什么会有两个明显的跳跃？

第一个跳跃点是在临界质量处，这好理解：当η＜η*时拉力小于摩擦力，小车静止不动，一旦η＞η*小车就会运动，所以在η*处有一个跳跃。另一处跳跃发生在刚好冲出台面的情况，也许第二阶段小车到达危险位置时水平速度为零，但是进入第三阶段后，小车绕台面边缘A转动起来，又会产生水平的速度分量。

以质量比η=30%为例，看看小车在运动过程中各种力随时间(图9)或位移(图10)的关系。可以看出水平方向的合力(绳子拉力分量减去摩擦力)开始大于0使小车加速，当小车前缘出了台面后水平分量小于0使小车减速。可以看出小车前缘在到达台面边界时各种力都有突变，以压力变化为例，可以从方程(1)和方程(3)中解出跳变的幅度，令方程(1)中θ=90°，方程(3)中β=0，˙β=0，有从而得到小车第一阶段最后时刻的压力为N-=m1(m1+m2)g/(m1-m2μ)=1383 N，而第二阶段初始时刻压力为N+=(m1+m2)g=1300 N，其他力的跳跃也可以类似分析。

图9 力随位移变化关系

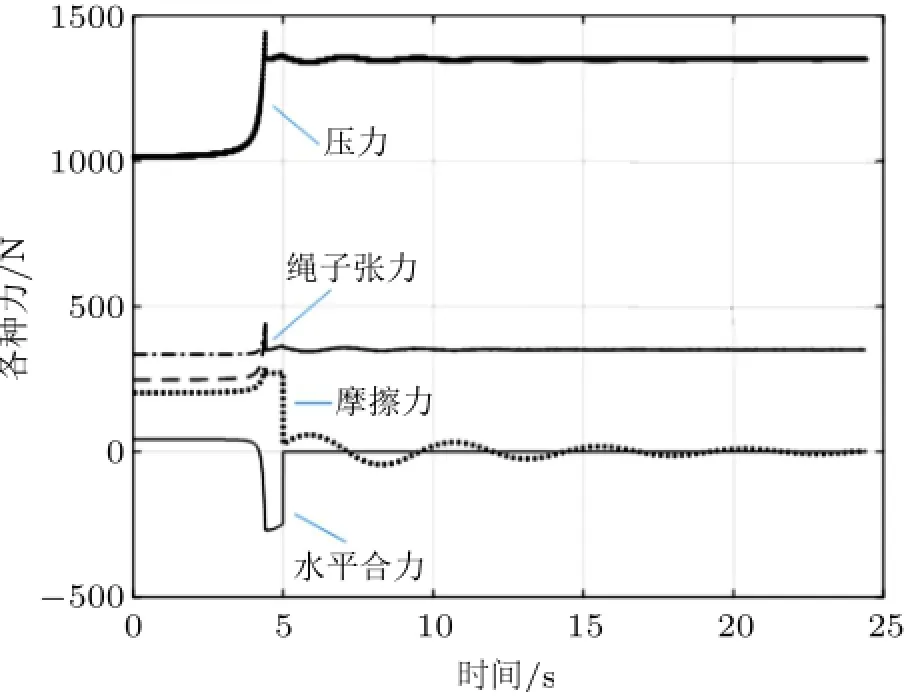
图10 力随时间变化关系

最后可以看看小车冲出台面但最终停在台面上的各种曲线变化：图11中绳子角度开始接近与台面平行，后来摆动起来，角度产生周期性变化，由于有空气阻尼，最终静止。图12中摩擦力开始较小，小车接近台面边缘时，绳子拉力方向接近垂直，压力增加导致摩擦力增加，小车冲出台面后摩擦力趋于零，但由于配重的摆动，导致摩擦力的方向也会变化。

图11 角度随时间的变化关系

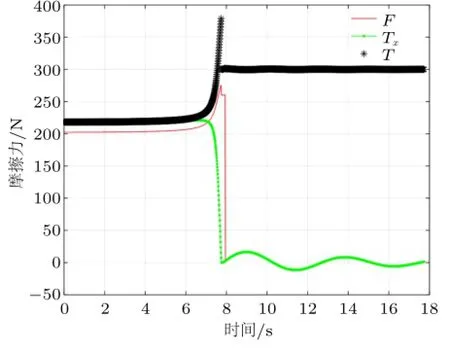
图12 力随时间的变化关系

7 结语

悬崖勒马问题看上去简单，但是过程中自由度数目一直在变化，可以让学生了解到实际问题是如何建模、分析、计算的。本文解释了悬崖勒马的原理，给出了配重与小车的临界质量比，给出了安全位置和危险位置，分析了压力突变的范围，并对小车运动的整个过程进行了数值仿真，得到了丰富的数据、曲线和动画演示，可让学生对这一问题有全面、深入的了解。