岩石单轴压缩实验边界条件反演研究1)
2021-01-06吴佳宁邢同振宋义敏
吴佳宁 邢同振 宋义敏
*(北方工业大学土木工程学院,北京100144)
†(北京理工大学宇航学院,北京100081)
在人类生产和实践过程中,岩石是重要的生产材料,岩石材料的力学参数作为采矿、岩土、地下空间等工程在设计、施工和运行维护过程中的基础数据,对于整个工程和人员的安全保障影响重大。因此,对于岩石的边界条件和力学参数的研究具有重要的理论和实践意义。
对于岩石的边界条件和力学参数的研究,专家学者取得了一些有意义的成果。袁风波[1]基于地应力实测数据和数值模拟手段,使用神经网络算法和遗传算法进行优化,反演了岩体地应力场;陈亮[2]基于有限元基本原理,建立结构的数值模型,反演了桁架、梁和方板的力学边界条件;邱道宏等[3]基于主应力测量数据,建立数值计算模型,利用神经网络反演了初始地应力场;黄亚哲[4]将计算得到的边界条件和力学参数代入到有限元数值模型中,通过小波神经网络优化求解的方法反演了初始地应力场;付玉华等[5]基于实测的离散点应力值,使用有限元法和有限差分法优化目标函数,反演了构造应力场边界力。通过以上研究成果可以看出,反演方法是获取岩石边界条件和力学参数的重要手段。
本文基于有限元方法推导岩石参数反演方程组,通过数字散斑相关方法观测岩石单轴压缩实验的位移场,将位移场作为已知量,反演岩石单轴压缩实验的边界条件和岩石试件的力学参数。
1 反演方程组推导
单元基本方程为[6]

式(1)中,k为单元刚度矩阵,q为节点位移矩阵,F为节点外载荷矩阵,单元刚度矩阵k展开形式见式(2)。i,j,m为三角形单元的3个节点。
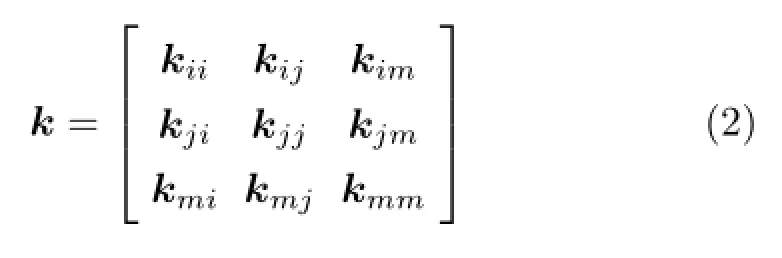
以两个3节点三角形单元为例,推导参数反演方程组。图1是一个厚度为t的正方形,划分为e1和e2两个3节点三角形单元,共4个节点,节点顺序按逆时针排列。
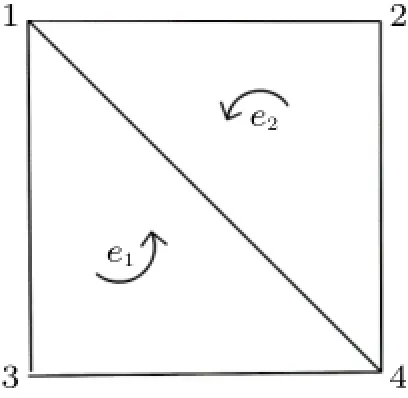
图1 单元示意图
单元e1和e2的单元刚度矩阵ke1和ke2表示为

整体刚度矩阵是各单元刚度矩阵之和,即

每个子矩阵都可以由式(6)计算得到
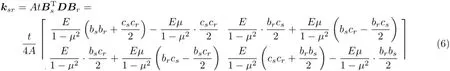
式中,A为单元面积,t为厚度,μ为泊松比,E为弹性模量,s=i,j,m,r=i,j,m。将式(6)和式(5)代入基本方程,得到参数反演方程组T为已知参数矩阵
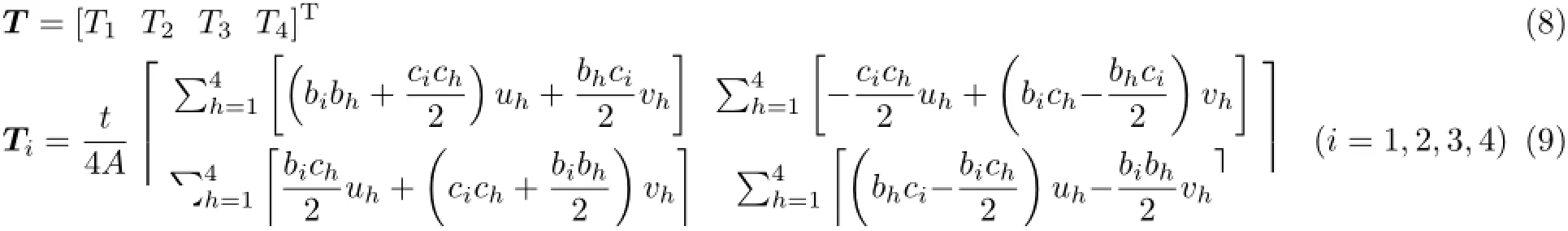

式中,h代表与i在同一单元的所有节点号。C为未知弹性参数矩阵,F为节点外载荷矩阵
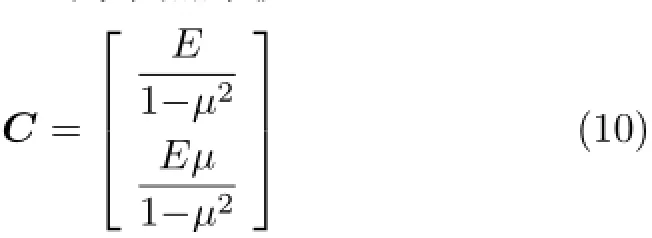
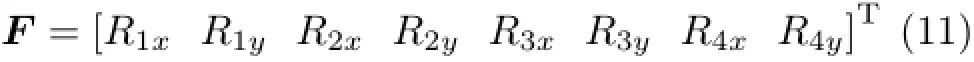
将两单元拓展到多单元,假设节点数为n,则未知弹性参数矩阵C不变,已知参数矩阵T和节点外载荷F分别为
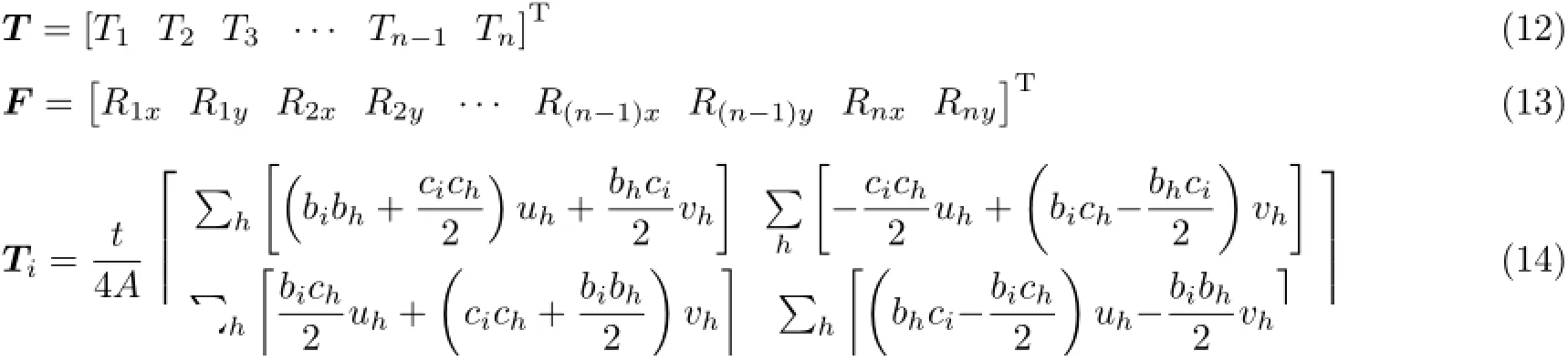
式中,i=1,2,···,n。
2 岩石单轴压缩实验
2.1 实验准备及过程
实验选取红砂岩材料,制成长方体试件,长和宽均为50 mm,高为100 mm,通过精细打磨的方式使试件各个端面平整,选择一个长50 mm,高100 mm的平面制作人工散斑场。
实验系统分为加载系统和数字散斑相关方法图像采集系统。加载系统使用RLJW-2000型液压伺服控制试验机,对试件施加单向压缩载荷,使用位移加载方式,加载速度大小为0.1 mm/min。数字散斑相关方法图像采集系统由CCD相机、光源和计算机三部分组成,图像采集速率为每秒2帧,图像分辨率为1600×1200像素,物面分辨率为每像素0.088 mm。
实验开始前,在试件上下端面和上下压板上均匀涂抹一层润滑剂,减小摩擦力的作用效果,调试试验机压头与试件上端面稍微接触,调整CCD相机的位置、焦距和光圈,使成像效果最佳;实验开始,试验机对试件进行单轴压缩加载,试件上端保持固定,下端产生向上的位移;同时,图像采集系统开始采集散斑图像,直到试件发生破坏,停止加载和数据采集;实验结束后,对采集到的数据进行计算分析。
2.2 实验分析及结果
使用数字散斑相关方法计算加载过程中试件的变形场,单轴压缩的应力与应变曲线如图2所示,将加载初始时刻采集的散斑图像作为参考图像,在应力与应变曲线上按照等应变间隔选取标识点1~5,计算红砂岩加载过程中5个标识点对应时刻的位移场,标识点1~5对应的采集时间、载荷、应力和应变量值见表1。
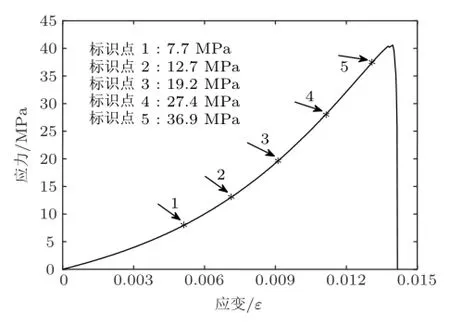
图2 单轴应力与应变曲线
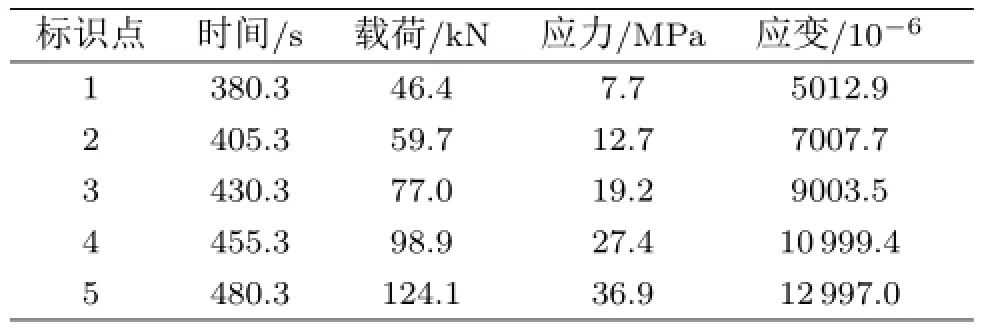
表1 标识点1~5参数值
以标识点5时刻为例,试件位移场云图如图3所示。随着加载进行,在水平方向上,试件由中间向左右两侧移动,位移场等值线出现“X状”分布,这是由试件上下端面与压机之间存在摩擦力导致的;在竖直方向上,随着加载进行,等值线呈水平分层分布,在加载过程中,试件上压板保持固定,下压板施加向上的位移,竖直方向的等值线量值由上至下逐渐增大。

图3 标识点1~5位移场云图
根据试件尺寸,将试件划分为数量一定的3节点三角形单元,以3×5网格为例,单元划分网格示意图如图4所示。在水平方向上,将散斑场平均分成3等份,竖直方向上平均分成5等份,共划分了30个单元,24个节点。以实验计算得到的位移场为已知量,将单元内的已知点位移值代入到有限元方程中,优化求解各个节点位移。
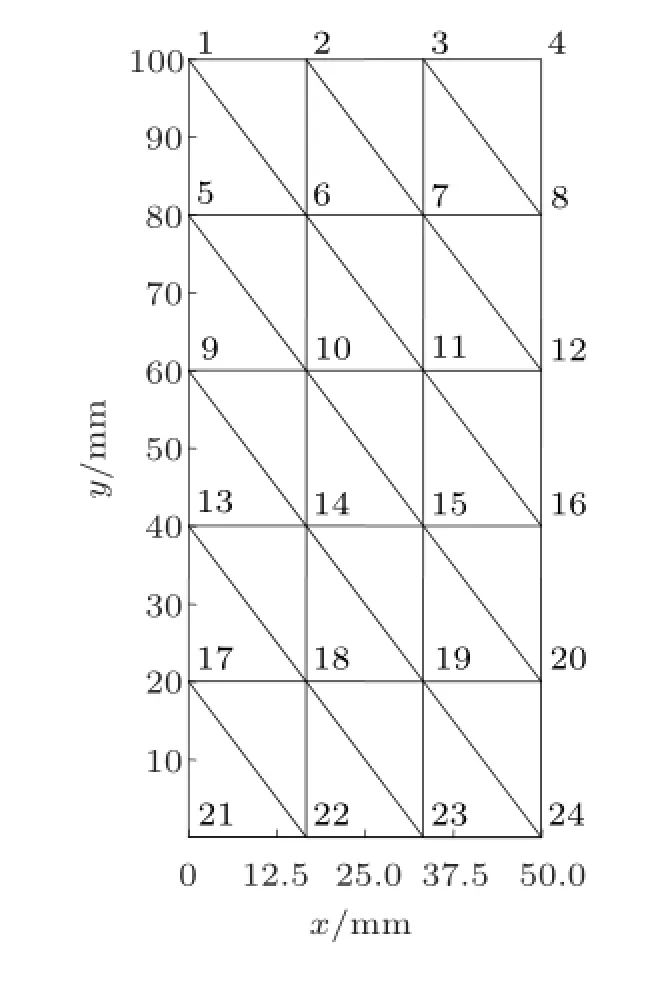
图4 网格划分示意图(3×5)
节点位移计算方法如下:假设在任意一个节点为i,j,m的三角形单元中,数字散斑相关方法计算已知点的数量为n,位移为u1,v1,···,un,vn,通过已知点坐标计算的形函数为Ni1···Nin,Nj1···Njn,Nm1···Nmn,三角形单元3个节点的坐标在划分网格时已经确定,将以上数据代入到式(15)中,采用最小二乘法进行优化,计算得到节点位移值ui,uj,um,vi,vj,vm。
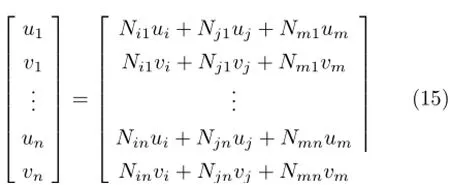
由于一个节点可能存在于多个单元中,因此在不同单元中,同一个节点计算得到多个位移值,将多个位移值的均值作为该节点的划分网格节点位移值。例如,在标识点5中,图4中的所有网格节点位移插值结果见表2。
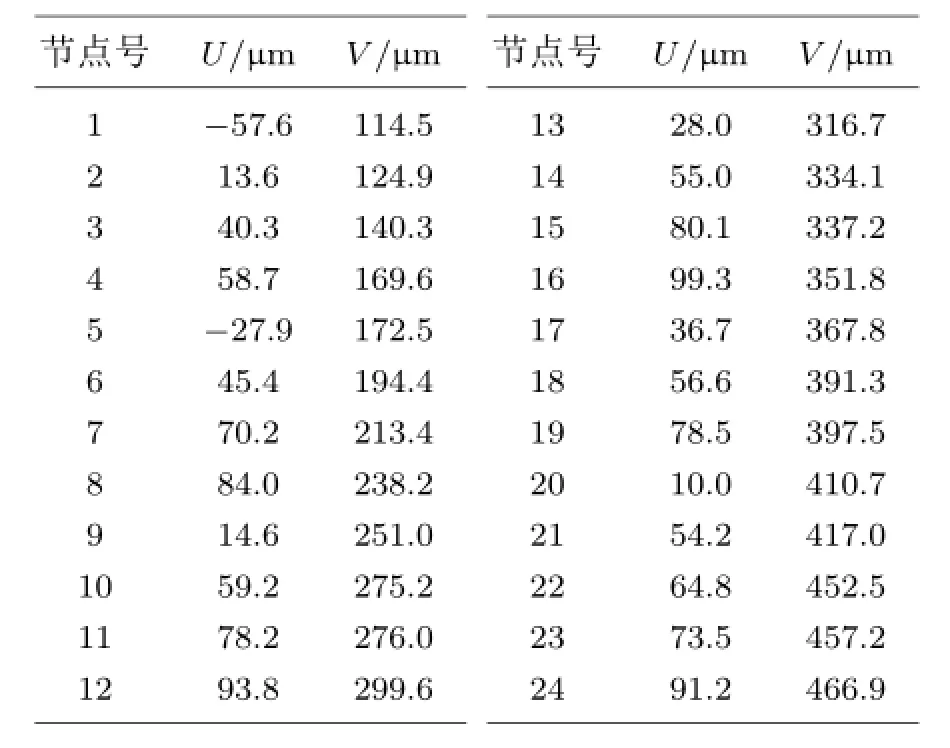
表2 节点位移计算结果
试件上端面竖直方向位移值为0,根据实验加载中的力和位移关系,认为外载荷平均分布到试件下端面的各个节点上。由于单轴压缩加载位移等值线在水平方向大致呈“X状”分布,试件上下端面与上下压板之间存在摩擦力,试验机和数字散斑采集系统均不能测量得到边界条件摩擦力的量值大小,需对试件上下端面水平方向节点外载荷进行反演。根据单轴压缩实验条件设置,试件上端面节点承受水平方向的节点外力,试件下端面节点承受水平和竖直方向的节点外力,其余节点不承受外力。
3 边界条件和弹性参数反演结果
在参数反演方程组式(7)中,假设岩石的弹性模量E和泊松比μ未知,散斑场划分3节点三角形单元网格的节点数共为n个,其中,上/下边界节点数为n1个,参数反演方程组是由2n个方程和2n1+2个未知量组成的超定方程组,使用最小二乘法进行优化,计算得出红砂岩单轴压缩的弹性模量E、泊松比μ和上下端面的水平方向外载荷值。其中,弹性模量E的初始值为8 GPa,上限为100 GPa,下限为1 GPa,泊松比μ的初始值为0.25,上限为0.5,下限为0,停止迭代条件为未知数的变化差值小于10-8。优化计算部分程序如图5所示。

图5 优化计算部分程序
将散斑场划分为5×10的3节点三角形网格单元,即在水平方向上将散斑场平均分为5等份,共10个单元,在竖直方向上将散斑场平均分为10等份,共10个单元。分别计算5个加载时刻的弹性力学参数和岩石单轴压缩实验上下端面边界条件,计算结果见表3,其中,FX1~FX6为试件上端面水平方向的节点外力,FX7~FX12为试件下端面水平方向的节点外力,FY为已知的试件下端面竖直方向的均布节点外力。
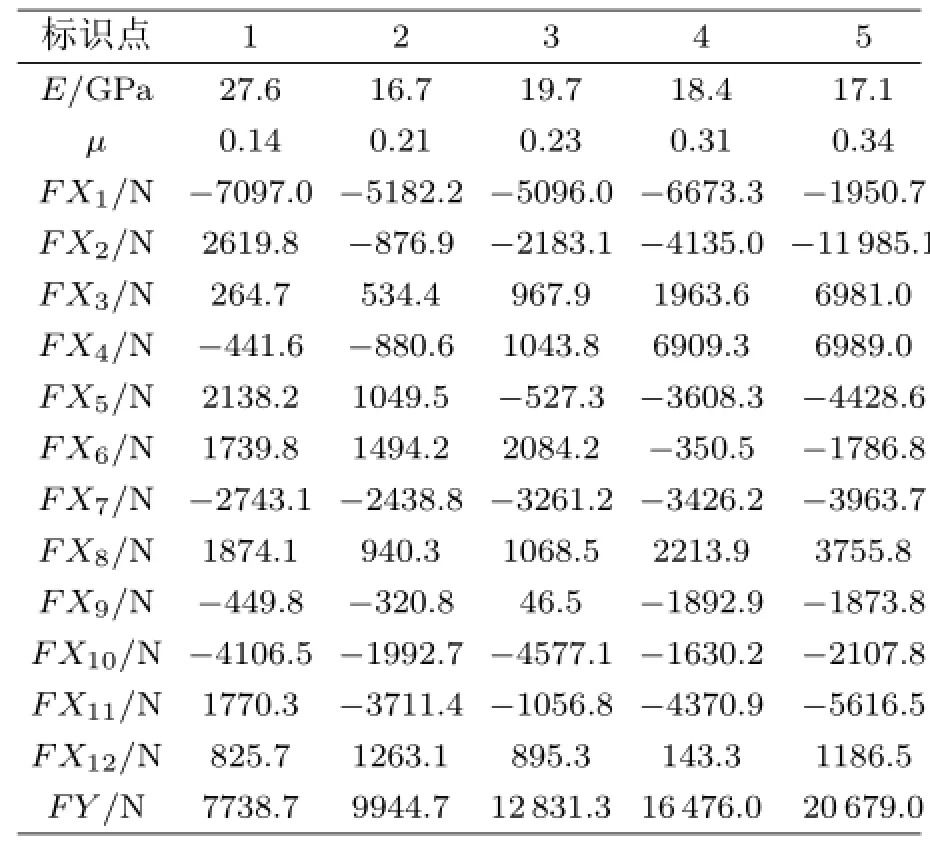
表3 标识点1~5计算结果
表3 的计算结果如图6和图7所示。通过图6可以看出,水平方向的相邻节点外载荷方向可能不一致,量值大小也不完全统一,计算结果与节点位移量值大小和方向密切相关,由于岩石是非均质的材料[7-8],某个位置的微小裂隙或者结构构造弱化都会导致其在加载过程中出现较大裂隙,位移量值比该点周围点的位移量值大,进而导致力的特征差异。从图7中可以看出,随着加载进行,弹性模量为18 GPa左右,加载后期趋于稳定,泊松比在0.14~0.34之间,随加载进行呈现逐渐增大趋势。
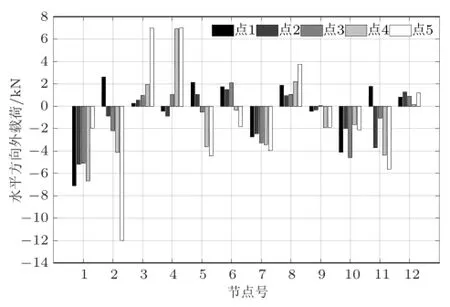
图6 边界条件计算结果
4 结论
本文通过有限单元法和数字散斑相关方法对岩石单轴压缩实验的边界条件和弹性参数进行反演。可以得到如下结论:
(1)利用本文所发展的方法,可以实现材料的边界条件和弹性参数反演。
(2)随着加载进行,反演得到的弹性模量为18 GPa左右,并且加载后期趋于稳定;泊松比在0.14~0.34之间,随加载进行呈现逐渐增大趋势。
(3)在水平方向上,相邻节点外载荷的方向和量值大小具有一定差异,产生此种结果与岩石材料的非均匀性及各个节点的位移量值差异较大有关。
