碳纤维织物摩擦力的影响因素及其交互作用

2021-01-06解锡明

毛纺科技 2020年8期

解锡明，吴宁，李帅

(天津工业大学纺织科学与工程学院，天津 300387)

碳纤维增强复合材料由于其比强度、比刚度高和轻质化等优点正逐渐取代传统金属材料而被广泛应用于航空航天、汽车、风电和船舶等领域。不同于金属材料，纤维增强复合材料层合板是由各向异性的单层织物增强体铺层后和基体复合固化而成，其损伤过程和破坏机制异常复杂[1-3]。

液体模塑成型技术(LCM)是复合材料成型工艺的重要加工方法之一[4-6]。与传统的手工铺层或高压蒸馏法相比，该方法适用于大批量生产，并且可获得高达60%的纤维体积分数。但在LCM合模时，织物及其纱线会与模具发生摩擦，而摩擦往往会引起织物的局部缺陷，如起皱或纱线断裂[7]，这会影响树脂的流动与浸渍，造成最终成品力学性能下降[8-10]。

因此，对LCM合模时织物与模具之间的摩擦行为进行研究，有助于更好地理解、掌握和优化LCM过程。为此，越来越多的学者关注于织物与模具之间的摩擦行为与复合材料最终成品之间的关系[11-13]。AVGOULAS等[11]用平板摩擦法，并结合自行开发的光学微观观察法探究了碳纤维单向布在LCM工艺中合模的摩擦机制。试验结果表明：随着压强从6.4 kPa增加至320.0 kPa，碳纤维单向布与平板的真实接触长度从理想长度的1.5%增加至11.0%，由此造成了摩擦力的增加。并结合界面剪切模型[14]与赫兹接触理论[15]验证了试验结果。SACHS[13]为了研究Twintex@PP(一种玻璃纤维与聚丙烯的混纺织物)与金属模具之间的摩擦行为，设计了7种不同的平板摩擦装置。研究结果表明：7种不同的摩擦装置测得的平均摩擦因数相差不超过5%。平均摩擦因数不同的原因在于不同的摩擦装置导致的加载力分布的不匀。NAJJAR等[12]为了模拟LCM工艺合模中的织物与模具、织物与织物之间的摩擦行为，采用自制的摩擦装置测试并分析了0.28 tex碳纤维织物(G1151)间以及0.28 tex碳纤维织物与有机玻璃模具、铝制模具之间的摩擦因数。此外，还分析了加载力与温度对上述3种摩擦副的摩擦性能影响。试验结果表明：织物/织物、织物/有机玻璃、织物/铝的摩擦行为具有各向异性，其摩擦因数均随着加载力与温度的升高而下降。MONTERO[10]为了深入了解摩擦现象对玻璃平纹织物造成的影响，研究了0°/0°、0°/90°、90°/90°和0°/45°这4种铺层方式在不同加载力与摩擦速度的情形下的织物间的摩行为。研究结果表明：0°/0°与0°/90°的摩擦特性相似，且压力的增加会导致4种铺层方式的摩擦因数的减小，而速度的增加则会导致4种铺层方式的摩擦因数增大。

以上学者对织物间的摩擦以及平板与织物间的摩擦行为展开了大量的研究，但根据复杂结构复合材料的设计需要，通常会使用不同曲率的模具及厚度的织物预制体。然而，现有研究还未涉及到具有曲率的模具与多层织物之间的摩擦行为。本文研究采用自制的摩擦装置，结合响应面分析法研究织物层数、摩擦速度、加载力、磨头曲率的交互作用对碳纤维平纹织物表面摩擦力的影响。

1 试验部分

1.1 主要材料

碳纤维平纹织物示意图见图1。该织物由江苏恒神股份有限公司织造，经纬向密度均为45根/(10 cm)。织物经纱纬纱均为HF40-12k国产碳纤维，该型号的碳纤维纱线拉伸强度为5 490 MPa，模量294 GPa，泊松比为0.3。

图1 碳纤维平纹织物示意图

3种不同曲率的磨头示意图见图2。其材料为43CrMoV轴承钢，曲率为0、0.24、0.48。

图2 3种不同曲率的磨头示意图

1.2 摩擦试验仪器与方法

采用美国布鲁克公司的摩擦磨损试验机(UMT-TriboLab)，并在试验中采用单向运动模式，加载力传感器规格为0～20 N。

为了模拟合模过程中碳纤维平纹织物与磨头之间的摩擦行为，设计了一套摩擦试验装置，摩擦试验上下夹具装置示意图见图3。如图3(a)所示，上端的固定器可插入具有3种不同曲率且长度为20 mm的金属磨头。试验所用碳纤维平纹织物的尺寸为85 mm×40 mm。为了防止碳纤维平纹织物在摩擦试验中脱散，使用无纺布胶带将其四边固定，并保证织物未被无纺布胶带覆盖的区域为60 mm×30 mm。然后，使用自制的底层夹具沿着织物的纬向将其前后两端固定。金属磨头插入固定器后，将固定器与传感器相连接，通过Z向加载器对固定在下方底座上的碳纤维平纹织物施加法向载荷(N)，通过电磁传感器记录试验过程中摩擦力(F)的变化。试验时，上方磨头固定不动，下方织物沿纬向进行一次单向运动以实现碳纤维平纹织物与磨头之间的摩擦。

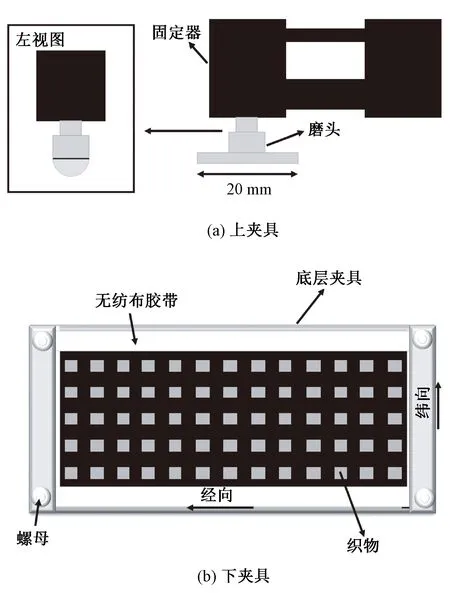
图3 摩擦试验上下夹具装置示意图

1.3 损伤表征

将碳纤维纱线从磨擦后的平纹织物中抽取出来，再使用日本威信VIXEN PC-230 数码显微镜 PC-230拍取侧面图像；之后利用ImageJ 1.46 r软件提取图片边缘信息，使得图片中碳纤维纱线的毛羽变得清晰易于分辨；接着使用该软件的自由选取功能，选取出纤维束上下2个部分毛羽区域，得到该区域部分的灰度值曲线。灰度值越大，则表明毛羽量越多，即纱线损伤越大[16]。

1.4 试验方案

由于LCM工艺涉及到织物层数、摩擦速度、加载力、磨头曲率，因此这4个参数被选定为试验参数。设置织物层数为1、3、5层，且方向铺层均为90°；摩擦速度选定为0.1、1.0、1.9 Hz(即2.4、24.0、45.6 mm/s)，该滑动速度范围包涵了多层织物成型过程中滑动速度的范围[10]；实际生产过程中，复合材料成型的压强范围多为0～100 kPa[13]，故测试压强选为16.7、41.7、66.7 kPa。由于名义接触面积为120 mm2，故施加的加载力设定为2、5、8 N。

根据响应面分析软件提供的模型，设织物层数A、摩擦速度B、加载力C、磨头曲率D这4个参数为自变量；设摩擦测试时产生的摩擦力为响应值Y。响应面因素水平编码表见表1。

表1 响应面因素水平编码表

2 结果与讨论

2.1 响应面数据分析

利用Design Expert 8.0.6 软件，根据 Box-Behnken 的中心组合设计原理,设计了4因素3水平共29个试验点的响应面分析试验，并对试验数据进行回归分析。响应面试验设计及结果见表2。

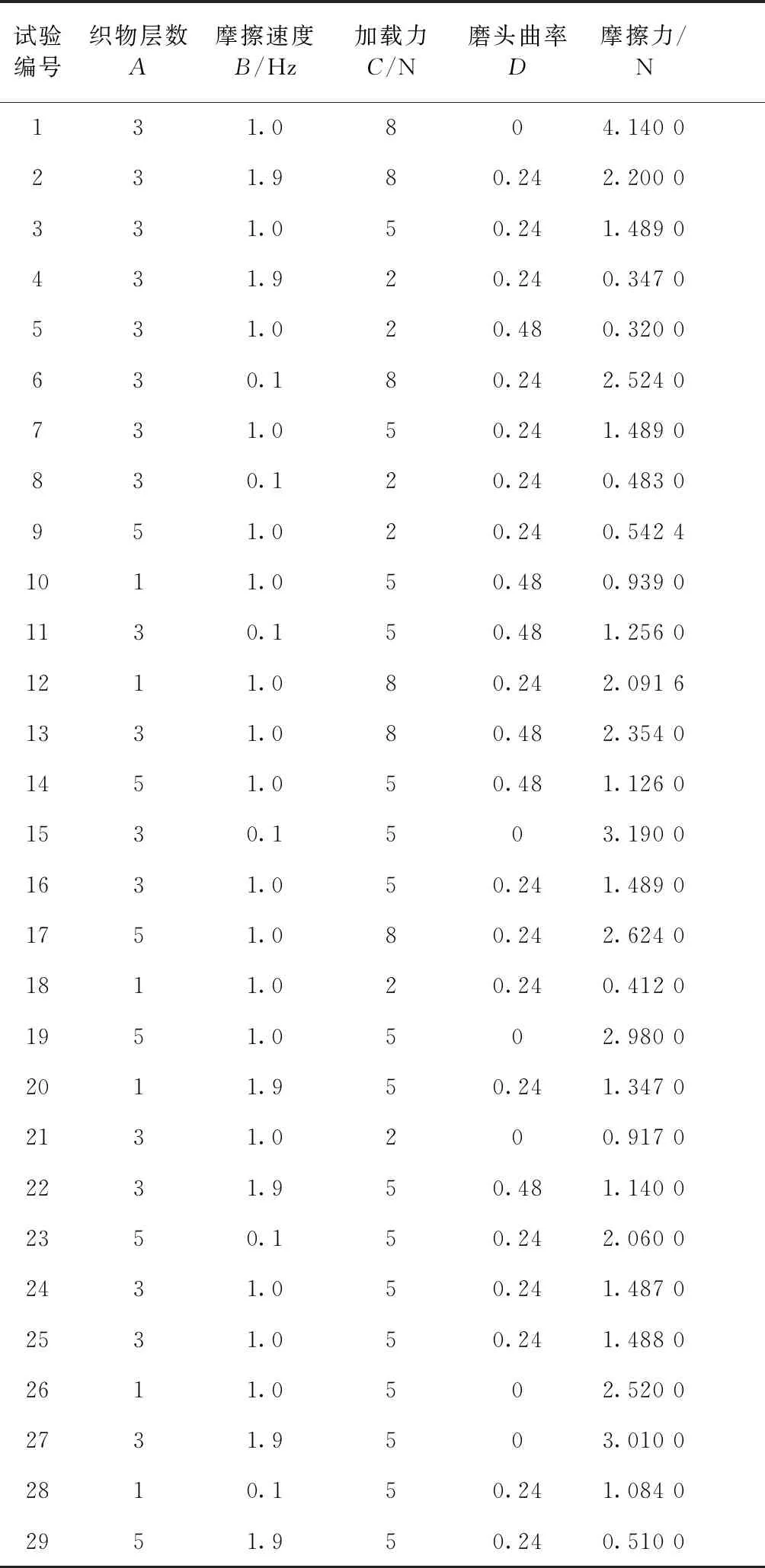
表2 响应面试验设计及结果

采用方差分析(ANOVA)确定二次回归模型的显著性和适应度，以及显著的相互作用对响应值摩擦力的影响。响应面方差分析结果见表3。P值即概率，反映某一事件发生的可能性大小。统计学根据显著性检验方法所得到的P值，一般以P<0.05为显著，P<0.01为非常显著，其含义是由抽样误差所致的样本间的差异概率小于0.05或0.01。若二次回归模型P值小于0.000 1,表明该模型在95%置信水平下显著。由表3可知，织物层数A，加载力C，磨头曲率D对摩擦力的产生的影响较大。但当P值>0.1，则表明模型项不显著[17]。由于摩擦速度B的P值>0.05，说明尽管织物层数B对摩擦力会产生影响，但引起的摩擦力变化幅度并不大。

表3 响应面方差结果分析

失效拟合项决定了二次回归模型的精确程度。一般情况下，如果失效拟合项不显著，则表明模型与试验数据拟合良好。失效拟合项的P值越大，则说明模型越精确，回归效果越显著。在本文研究中，发现缺乏拟合参数的P值分别为0.122 2，且大于0.050 0，说明二次回归模型充分描述自变量(织物层数、摩擦速度、加载力、磨头曲率)与响应值(摩擦力)之间的关系。

决定系数(R2)充分反映了因变量与自变量(预测变量)之间的关系。R2值介于0与1之间，若R2越接近1，则表明回归拟合效果越好，一般认为超过0.8的模型拟合度比较高。由表3可以看出，R2值为0.964 5，说明二次回归模型的拟合程度高。

表3中调整R2(0.928 0)及预测R2(0.795 2)值均接近 1，且二者的差值为0.13，小于0.2，这表明二次回归模型和试验数据之间具有良好的一致性。

如表3所示，本文研究中的充分精度为21.134 0，而充分精度一般要求大于4，故二次回归模型适用于本文摩擦试验。此外，变异系数(CV值)较低，为15.96%，表明试验数据准确可靠[18]。

残差被定义为试验值和预测值之间的偏差。如果试验误差是随机的，二次回归模型具有合理性，则残差服从正态分布。为了确定残差是否服从正态分布，首先需要分析二次回归模型的充分性。利用拟合正态分布对残差进行预测，并与试验得到的残差进行对比。响应面试验残差分析见图4。

图4 响应面试验残差分析

由图4(a)可知，残差与正态概率的函数曲线近似一条直线，故残差服从正态分布。图4(b)为残差与预测摩擦力对比，可以看出，数据点在图中随机分布，说明原始测量值与响应值无关。由此可以推断，二次回归模型能够较好地描述织物层数、加载力、摩擦速度、磨头曲率对摩擦力产生的影响。图4(c)为摩擦力与4个试验参数之间的离群点t图，表示每次试验运行的残差值。可以根据图4(c)确定哪一次试验运行有较大的残差，可以看出，所有的研究残差都在[-3,3]区间内，说明拟合模型对响应值有很好的逼近性。综上所述，残差服从正态分布，二次回归模型具有合理性。

2.2 织物层数与摩擦速度的交互作用分析

由表3可知，在模型的交叉项中只有AB、CD对磨头与碳纤维平纹织物间的摩擦力有着显著性影响。其中AB的P值为0.039 4，CD的P值为0.003 8，故只对织物层数与摩擦速度、加载力与磨头曲率的相互作用进行讨论。

织物层数与摩擦速度的交互作用对摩擦力的影响见图5。图5(a)等高线的形状反映了各因素之间交互作用的强弱，等高线形状越接近椭圆，则表明各因素之间的交互作用越强；等高线形状越接近圆形，则各因素间的交互作用越弱。

图5 织物层数与摩擦速度的交互作用对摩擦力的影响

图5(b)响应面的形状反映了各因素对于响应值的显著程度。响应面越陡，则表明显著性越大。由图5可知，虽然织物层数与摩擦速度的交互作用对摩擦力有着一定的影响，但是影响程度有限。因此就总体趋势而言，随着织物层数的增加并伴随着摩擦速度的减小，磨头与织物间的摩擦力逐渐增大。如图3(b)所示，碳纤维织物仅两端被固定，并没有完全被约束。因此在摩擦试验过程中，碳纤维织物层与层之间存在相互运动。当相邻两层碳纤维平纹织物的纬组织点因上述情况而产生相互碰撞时，便会造成摩擦力增加。织物层数越多，这样的组织点间发生的碰撞的频率就越多，由此产生了摩擦力随着织物层数的增加而增加的现象。当摩擦速度增加时，则磨头与最顶层碳纤维织物的接触时间就会减少，导致磨头与织物间的黏附力减弱[19]，因此摩擦力随着摩擦速度的增加而减小。

2.3 磨头曲率与加载力的交互作用分析

磨头曲率与加载力的交互作用对摩擦力的影响见图6。可以看出，其地形图的等高线为椭圆形，故可以直观地得出磨头曲率与加载力之间的交互作用对摩擦力有着较为明显的影响。因此，就总趋势而言，当磨头曲率的减小并伴随着加载力的增加，则磨头与织物间的摩擦力逐渐增加。这是因为，当磨头曲率逐渐减小时，磨头的弯曲程度逐渐减小，故在相同条件下磨头与碳纤维平纹织物间的接触面积越大。由界面剪切理论可知[14],2个物体间接触面积越大，则物体间黏附力越大，因此摩擦力也就越大。

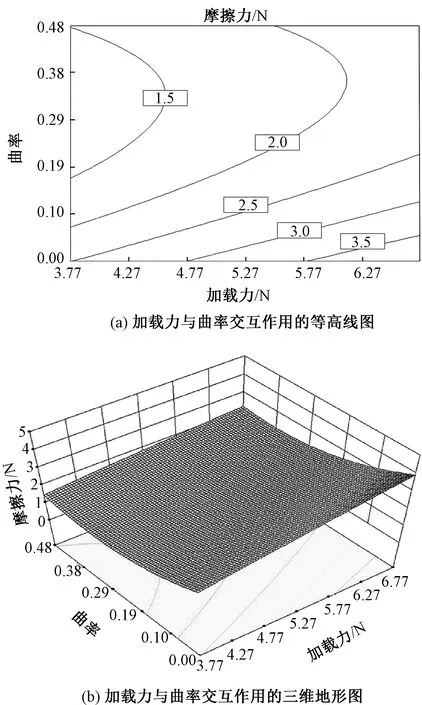
图6 磨头曲率与加载力的交互作用对摩擦力的影响

摩擦力的增加与接触面积有着紧密的联系。由赫兹理论可知，不同曲率的磨头与近似圆柱体的碳纤维长丝的接触可以简化为圆柱体与平板之间的接触[20]，故可得式(1)：

(1)

式中：Ar为磨头与织物间的真实接触面积，mm2；R为碳纤维长丝的半径, μm;L为磨头与碳纤维长丝的接触长度, mm;N为加载力, N;E*为磨头和碳纤维的等效模量；n为磨头与碳纤维长丝的接触根数。

由于碳纤维纱线的宽度会随着加载力的增大而增大，故磨头与碳纤维长丝的接触根数会随着加载力的增大而增加[21]。此外，磨头与碳纤维长丝的接触长度也会因为加载力的增大而增加[22]，且碳纤维长丝半径、磨头和碳纤维的等效模量均为常数，故由式(1)可知，加载力的增大会导致真实接触面积的增大，进而导致黏附力的增大，最终导致摩擦力增加。

磨头曲率对摩擦力变化规律的影响见图7。可知，磨头曲率不仅能够影响摩擦力的大小，还能影响摩擦力变化的规律。当磨头曲率为0.24和0.48时，其摩擦力-位移曲线近似正弦函数曲线；而当磨头曲率为0时(摩擦形式即为平板与织物摩擦)，摩擦力-位移曲线并没有明显的规律。这是因为磨头曲率为0.24和0.48时，磨头具有一定的弧度。

图7 磨头曲率对摩擦力变化规律的影响

在这样的情形下，当磨头与碳纤维平纹织物发生相对运动时，磨头会与平纹织物的纬组织点会发生碰撞，从导致摩擦力的增加，形成波峰[23]；由于摩擦方向是沿着经向，经组织点的高度较纬组织点高度低，磨头与经组织点的摩擦形式相当于磨头与纱线间的摩擦，故而形成摩擦力-位移曲线的波谷[23]。

碳纤维平纹织物磨损后的纬纱形貌见图8。磨头曲率不为零时，与磨头相接触的纬组织点在接触之后基本保持原来的形貌；而当磨头曲率等于零时，与磨头相接触的纬组织点在摩擦之后不仅会产生严重的形变(见图8(a))，而且其内部会发生严重的长丝取向紊乱(见图8(b))。这种碳纤维纬纱的损伤会极大地影响磨头与其之间的接触情形，造成摩擦力-位移曲线的无规律现象。

图8 碳纤维平纹织物磨损后的纬纱形貌

不同加载力作用下3种磨头曲率与织物间的摩擦力关系见图9。

图9 不同加载力作用下3种磨头曲率与织物间的摩擦力的关系

由图9可知，当加载力不大于5 N时，摩擦力随着磨头曲率的增加而下降；但当加载力为8 N时，曲率从0.24增加至0.48后，摩擦力却有所增加(从2.62 N增加至2.66 N)。该现象与摩擦对纤维长丝造成的损伤有关。纱线的损伤通常表现为毛羽量的增加，毛羽量的增加会加剧摩擦时碳纤维束内部相互作用，并最终导致摩擦力的上升。

2种磨头曲率下碳纤维纱线的灰度值见图10。可知，曲率为0.48时的纱线灰度值曲线基本上高于曲率为0.24的灰度值曲线。灰度值越高，则表明纱线产生的毛羽量越大。这是因为磨头曲率的增大造成真实接触面积的减小，故当加载力不变时，平纹织物中的碳纤维纱线所承受的压强增大，碳纤维纱线会因为较大的压强而产生损伤。