三支决策视角下的属性约简加速方法*

2021-01-06姜春茂刘安鹏

计算机工程与科学 2020年12期

姜春茂，刘安鹏

(哈尔滨师范大学计算机科学与信息工程学院，黑龙江哈尔滨 150025)

1 引言

三支决策[1 - 3]是在决策粗糙集理论[4]基础上提出的一种三分而治思想，其核心是将论域分为3个子集，分别对3个子集采取不同的策略来处理不确定性决策。为了提高知识约简的提取速率,Yao[5]利用渐进式粒度计算思想进一步提出了序贯三支决策。属性约简[6-8]作为粗糙集理论[9]的核心研究内容，常常受到众多学者关注，其核心是在给定度量准则的前提下删除冗余属性的过程。在实际应用中，研究者往往对特殊决策类中的数据格外关注。在此基础上，Chen等[10]提出了集成属性约简的概念。集成属性约简虽然平衡了各决策类的需求，但同时也增加了计算约简的时间消耗。为了提高属性约简的计算效率，本文借助序贯三支决策思想提出了一种加速方法。新方法每次向约简集合中添加属性的同时排除部分无关属性来提高约简计算效率，以降低时间消耗。

2 基础知识

在粗糙集理论中，一个决策系统可表示为一个二元组DS=〈U,AT∪D〉，其中，U是所有对象的集合，称为论域；AT是条件属性的集合；D为决策属性集合且AT∩D=∅。

定义1给定一个决策系统DS，当D的取值都为离散型时，论域上的划分如下所示：

U/IND(D)={X1,X2,…,Xq}

(1)

其中，对于∀Xp∈U/IND(D),Xp表示第p个决策类。IND(D)={(x,y)∈U×U:∀ai∈AT,ai(x)=ai(y)},ai(x)表示样本x在属性ai上的取值。

另外，[x]D表示与x属于同一个决策类的样本集合。

传统粗糙集模型仅适用于处理离散型数据，不适合处理实际应用中的连续型或混合型数据。Hu等[11]提出了邻域粗糙集模型，该模型有效解决了传统模型在数据离散化后信息的丢失问题。具体方法是通过条件属性提供的信息计算样本间的距离，通过距离构造样本的邻域关系，最终借助邻域关系来处理复杂型数据。

定义2[12]给定一个决策系统DS,给定邻域半径δ，邻域关系可定义为：

N= {(x,y)∈U×U:rA(x,y)≤δ}

(2)

其中，∀x,y∈U,rA(x,y)表示样本x与y之间的距离，本文采用欧氏距离来计算；A为属性集合。

进而可以得到样本x的δ邻域为：

δA(x)= {y|rA(x,y)≤δ}

(3)

其中，δ为邻域半径，且δ>0。

定义3给定一个决策系统DS,U/IND(D)={X1,X2,…,Xq},∀Xp∈U/IND(D),Xp关于属性集合A的下近似集和上近似集可定义如下：

(4)

(5)

基于下近似集和上近似集的概念可将论域划分成3部分，即：正域POS(X)、边界域BND(X)和负域NEG(X)，形成基于粗糙集的三支决策[12]，其定义如下所示：

(6)

{x∈U|(δA(x)⊆Xp)∧(δA(x)⊆)}

(7)

(8)

其中，上标C表示补集。

可见，正域中的对象表示确定属于决策类Xp的样本，负域中的对象表示确定不属决策类Xp的样本，而边界域中的对象表示不确定属于决策类Xp的样本，相对应地可以分别给予接受、拒绝和不承诺(延迟决策)的语义解释。

3 属性约简

3.1 度量准则

根据应用场景的不同，属性约简有多种度量准则，常用的度量准则包括近似质量[13,14]和条件熵[15-18]等。本文以近似质量来构造约简求解的约束条件。下面给出近似质量的定义。

定义4给定一个决策系统DS,U/IND(D)={X1,X2,…,Xq},∀B⊆AT,D关于B的近似质量定义为：

(9)

其中,|X|表示集合X的基数。

显然0 ≤γ(B,D)≤ 1成立。γ(B,D)表示根据条件属性B,确定属于某一决策类别的样本占总体样本的比例。

本文计算约简时采用的是基于适应度函数的搜索方法，基于近似质量的属性重要性评价如下：

定义5给定一个决策系统DS,∀B⊆AT，B是DS中的一个关于近似质量的约简当且仅当γ(B,D)≥γ(AT,D)且∀B′⊆B,γ(B′,D)<γ(B,D)。

属性重要性的评价建立在样本粒化的基础上。样本粒化是通过条件属性提供的信息构造邻域关系，得到论域上粒化结果的过程。根据信息粒化结果可以计算某一度量值，进一步当某个属性加入到属性集合中，相应度量值的变化可以用来评估属性的重要度。由此，属性重要度如式(10)所示：

Sigγ(ai,B,D)=γ(B∪{ai},D)-γ(B,D)

(10)

其中ai∈AT。在属性约简中，常用的搜索策略包括添加属性、删除属性以及先添加后删除属性策略。本文采用添加式策略计算约简，即从空集开始逐个加入重要度最大的属性，直至满足约束条件为止。

3.2 传统添加式属性约简算法

胡清华等[12]提出了基于邻域粗糙集的前向贪心数值属性约简算法，该算法将属性重要性作为评价指标，通过贪心策略将当前重要度最大的属性添加至约简集合。该算法的具体描述如算法1所示。

算法1基于邻域粗糙集的前向贪心数值属性约简算法

输入：决策系统DS=〈U,AT∪D〉,半径δ。

输出：一个γ约简B。

步骤1计算γ(AT,D)；

步骤2B←∅；

步骤3 Do

(1)∀ai⊆AT-B,计算属性ai的重要度Sigγ(ai,B,D)；

(2)选出一个重要度最大的属性b,令B=B∪{b}；

(3)计算γ(B,D)；

Untilγ(B,D)≥γ(AT,D)；

步骤4返回B。

算法1的时间复杂度为O(|U|2·|AT|2),其中，|U|为论域中样本数目，|AT|为条件属性数目。该算法把所有决策类别作为一个整体计算，来选出重要度最大的属性，进而得到约简结果。该算法的好处是能够根据决策属性进行有效约简，但计算无法细化到具体的决策类别中。在实际应用中，研究者往往更加关注那些影响特定决策类别的属性，因而发展出集成属性约简的研究。

3.3 传统集成属性约简算法

首先给出集成环境下的局部近似质量的定义。

定义6[19]给定一个决策系统DS,U/IND(D)={X1,X2,…,Xq},∀B⊆AT,Xp关于B的局部近似质量表示如下：

(11)

结合式(9)和式(10)可以推导出集成环境下单个决策类Xp的局部属性重要度为:

Sigγ(ai,B,Xp)=γ(B∪{ai},Xp)-γ(B,Xp)

(12)

通过局部属性重要度分别求解各个决策类下重要度最大的属性，将得到的结果进行综合后得到侯选属性。集成属性约简算法[19]如算法2所示。

算法2传统集成添加式约简求解算法

输入：决策系统DS=〈U,AT∪D〉，半径δ。

输出：一个γ约简B。

步骤1计算γ(AT,D)；

步骤2B←∅；

步骤3 Do

T←∅；

Forp= 1：q

(1)∀ai⊆AT-B，计算属性ai的重要度Sigγ(ai,B,Xp)；

(2)选择aj，满足Sigγ(aj,B,Xp)= max{Sigγ(ai,B,Xp);∀ai⊆AT-B}；

(3)令T=T∪{aj}；

EndFor

选择T中出现频次最多的属性b，B=B∪ {b}；

(4)计算γ(B,D)；

Untilγ(B,D)≥γ(AT,D)；

步骤4返回B。

算法2的时间复杂度为O(q·|U|2·|AT|2),其中q为决策类的数目，|U|为论域中样本数目，|AT|为条件属性数目，T为所有决策类下选出的重要度最大的属性集。该算法的优势在于平衡了各个决策属性的需求，不足之处在于该算法在迭代过程中增加了计算量，导致求解约简的时间消耗增加。

4 基于三支决策的属性约简加速方法

为了缩短集成环境下属性约简的时间，本文提出了一种基于三支决策的属性约简加速方法。该方法的核心在于结合了序贯三支决策思想，在选择属性的同时排除部分无关属性，在迭代过程中减少侯选属性的数量，以达到降低时间消耗的目的。首先给出m层序贯三支决策S3WD(Sequential Three-Way Decisions)的构造过程如图1所示。

Figure 1 Construction process of sequential three-way decisions图1 序贯三支决策的构造过程

通过将BND(延迟决策域)中的候选属性迭代三分，最终转化为二支决策从而得到约简集合B，此时B=POS1∪POS2∪…∪POSm，m的取值与数据中冗余属性(NEG域中对象)和终止条件相关，且当约简的终止条件固定后，数据中冗余属性越多，所需的m值越小。

定义7给定第i层侯选属性集Pi(X),∀Xj⊆BNDi-1,Sig(Pi(Xj))表示属性Xj的重要度，则第i层的正域、边界域和负域划分规则如下所示：

(13)

BNDi(X)={x∈U|0<

(14)

(15)

其中，1≤i≤m，Sigmax(Pi(X))为第i层重要度最大的属性。Sig(Pi(Xj|[x]BNDi-1))为第i层的候选属性Xj的属性重要度。

4.1 属性约简加速算法

将加速方法应用到前向贪心数值属性约简算法中，具体步骤如算法3所示：

算法3基于三支决策的属性约简加速算法

输入：决策系统DS=〈U,AT∪D〉，半径δ。

输出：一个γ约简B。

步骤1计算γ(AT,D)；

步骤2B←∅;POS←∅;BND←AT;NEG←∅;

步骤3 Do

(1)∀ai⊆AT-B-NEG，计算属性ai的重要度Sigγ(ai,B,D)；

(2)将重要度最大的属性aj放入正域(POS)，将重要度为0的属性放入负域(NEG)，其余属性放入边界域(BND)；

(3)令B=B∪{ai}；

(4)计算γ(B,D)；

Untilγ(B,D)≥γ(AT,D)；

步骤4返回B。

算法3的时间复杂度为O(|U|2·(|AT|+|BND1|+…+|BNDm-1|)),其中|U|为论域中样本数目，|BNDi|为中间域属性数目。相比于算法1，算法3在迭代时将无关属性排除，避免了这些属性在约简过程中进行无效计算，因而对约简效率的提高有帮助。

4.2 集成属性约简加速算法

在集成环境下该加速方法同样适用，具体步骤如算法4所示：

算法4基于三支决策的集成属性约简加速算法

输入：决策系统DS=〈U,AT∪D〉，半径δ。

输出：一个γ约简B。

步骤1计算γ(AT,D)；

步骤2B←∅;POS←∅;BND←AT;NEG←∅;

步骤3 Do

T←∅；

Forp= 1：q

(1)∀ai⊆AT-B-NEG，计算属性ai的重要度Sigγ(ai,B,Xp)；

(2)选择aj,满足Sigγ(aj,B,Xp)=max{Sigγ(ai,B,Xp):∀ai⊆AT-B}；

(3)令T=T∪{aj}；

EndFor

选择T中出现频次最多的属性b放入正域(POS)，将重要度为0的属性放入负域(NEG)，其余属性放入边界域(BND)；

(4)B=B∪{b}；

(5)计算γ(B,D)；

Untilγ(B,D)≥γ(AT,D)；

步骤4返回B。

算法4的时间复杂度为O(q·|U|2·(|AT|+|BND1|+…+|BNDm-1|)),其中q为决策类的数目，|U|为论域中样本数目，|BNDi|为中间域属性数目，T为所有决策类下选出的重要度最大的属性集。加入三支决策加速方法后，算法4相比于算法2在约简的计算过程中降低了计算量。

5 实验与结果分析

为了验证所提加速方法的有效性，本文从UCI数据集中选取了8组数据进行实验，对应用了加速方法的算法(新算法)与传统算法在分类精度和时间消耗上的差异进行了比较。数据集的描述如表1所示。实验环境为PC机，双核1.00 GHz CPU,4 GB内存，Windows 10操作系统，Matlab R2016b 实验平台。

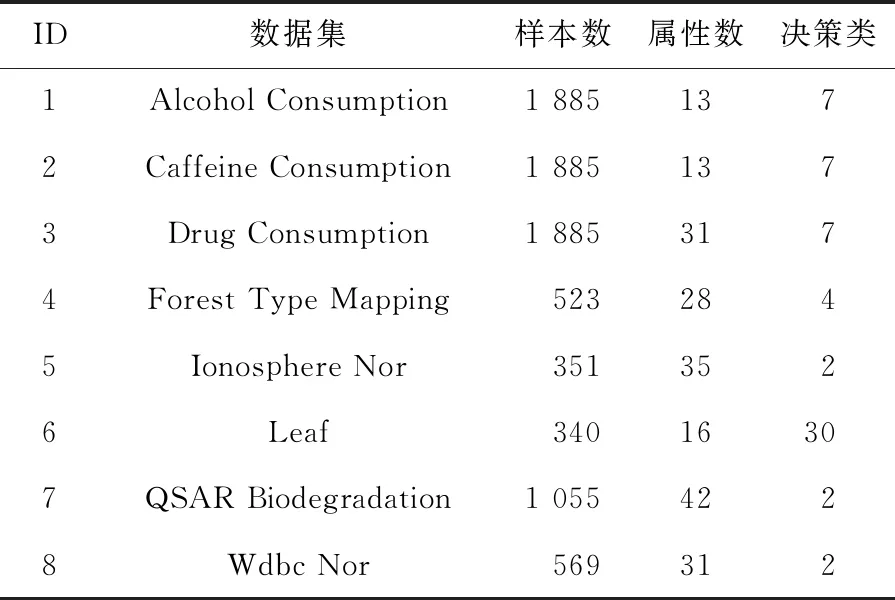
Table 1 Description of data sets表1 数据集描述

实验采用了5折交叉验证[20]的方法，选取10个不同的半径，分别为0.02,0.04,…,0.2。5折交叉验证的具体过程是将实验数据中的样本平均分成5份，即U1,U2,…,U5。第1次使用U2∪U3∪…∪U5作为训练集求得约简B1，使用U1作为测试集并利用B1中的属性计算分类精度；第2次使用U1∪U3∪…∪U5作为训练集求得约简B2，使用U2作为测试集并利用B2中的属性计算分类精度；依次类推，第5次使用U1∪U2∪…∪U4作为训练集求得约简B5,使用U5作为测试集并利用B5中的属性计算分类精度。

本组实验以近似质量为约简的度量准则，用邻域分类器NEC(NEighborhood Classifier)[11]和SVM分类器[21]对测试集中的样本进行分类。实验在全局环境和集成环境下分别进行，将传统算法与新算法进行对比分析。分别计算并比较了算法1～算法4的时间消耗及分类精度。

5.1 约简时间消耗对比

实验过程中记录了2种算法在近似质量度量指标上约简求解的时间消耗，详细的比较结果如表2所示。

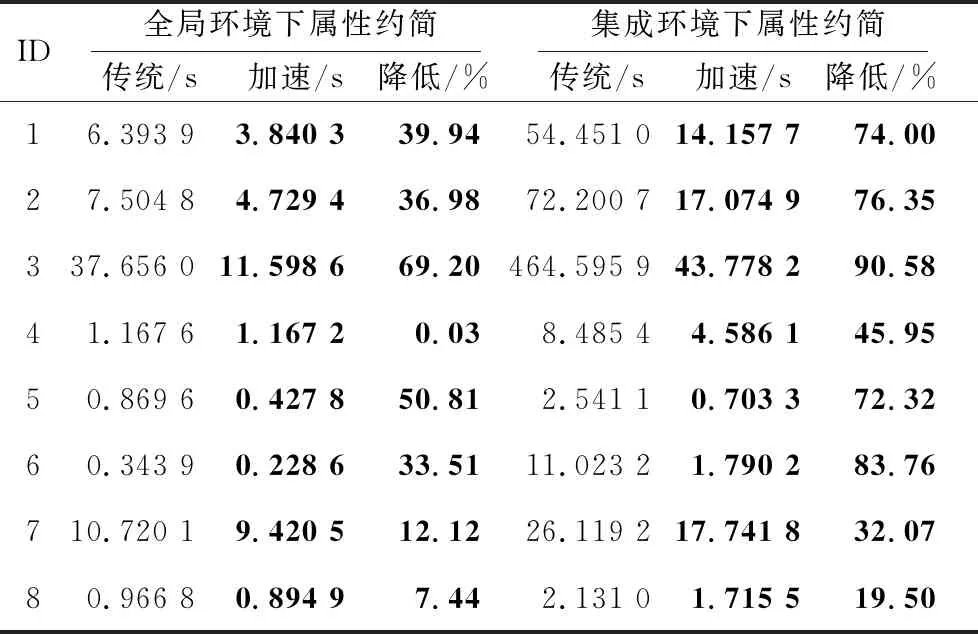
Table 2 Comparison of reduction time consumption between traditional and accelerated algorithms表2 传统算法与加速算法的约简时间消耗对比

由于篇幅有限，表2中数据集名称采用与表1中相同的ID号替代。通过实验发现，结合了三支决策思想的新算法，无论是在全局环境下还是在集成环境下，均能够有效降低约简的时间消耗。这是因为加速算法通过减少侯选属性的数量，降低了约简的计算时间。值得注意的是，在集成环境下每剔除一个冗余属性，会同步减少所有决策类别下约简的计算量，所以同一数据集在集成环境下应用三支加速约简方法，加速效果会更加明显。

5.2 约简结果的分类精度对比

图2和图3分别展示了在以近似质量为度量准则前提下，采用了加速方法的算法3和算法4与传统属性约简算法1和算法2在NEC分类器[11]和SVM分类器[21]上的分类精度对比。实验结果表明，在大部分半径下，算法3和算法4得到的分类精度优于算法1和算法2的，可以说明采用加速方法后的新算法具有不弱于传统算法的分类精度。

Figure 2 Comparison of classification accuracy between traditional algorithms and new algorithms in global environment图2 全局环境下传统算法与新算法的分类精度对比

Figure 3 Comparison of classification accuracy between traditional algorithms and new algorithms in ensemble environment图3 集成环境下传统算法与新算法的分类精度对比

5.3 实验分析

通过对比NEC和SVM分类器上约简结果的分类精度发现，新算法相比于传统算法拥有更好的分类性能。同时，新算法的时间消耗更低，说明基于三支决策的属性约简加速方法在保证分类器分类性能的前提下，有效降低了约简的时间消耗。这是因为新算法在每次循环选择属性时，仅判断划入边界域的侯选属性，减少了对无关属性的计算，因而在保证分类性能的同时能带来更好的时间性能。