混凝土楔形体在水电站导流围堰稳定性优化中的应用

黄 亮

(江西省宜春市水利水电工程监理有限公司，江西 宜春 336000)

0 引 言

围堰指的是在水利工程建设中，为了建造永久性水利设施而修建的临时性维护结构。其作用是防止水和土进入修建位置，方便围堰内部排水工作，为开挖基坑准备基础工作。围堰主要用于水工建筑中，一般在用完后拆除。围堰属于一种临时性挡水建筑物，对于结构来讲需要具有稳定、防渗、抗冲的性能[1]。在施工技术上，要方便使用后的拆卸，结构布局上水流平顺。楔形体下底面是梯形或平行四边形，上底面变成与下底面平行边平行的线段的一种拟柱体。过流围堰是指在一定条件下允许堰顶过水的围堰，过流围堰可以承担挡水任务，一般建设在洪枯流量比值大，水位变幅显著的河流。水电站导流围堰受到很多外部因素的干扰，为此研究混凝土楔形体在水电站导流围堰稳定优化中的应用，利用混凝土楔形体硬度大的优点，增强围堰的稳定性[2]。国内外施工水电站采用过流围堰的形式较多，国外早在1966年就已开始过流围堰工程的设计研究，截至到目前，已经建造成多种过流围堰工程，有着成熟的知识理论体系。国内也已经形成诸多的导流围堰工程，构建出多种行之有效的研究理论，增强了水电站工作过程的安全[3]。

1 混凝土楔形体在水电站导流围堰稳定性优化中的应用

1.1 控制围堰开裂特征参数

混凝土楔形体在水电站导流围堰运用时，导流围堰分布着一个渗流场，围堰的渗透系数较小，所以设定其量级为1E-10 m/s,围堰在接缝处的单位宽度流量就可表示为：

(1)

其中：b为围堰宽度；v为运动黏滞系数；vb为裂缝处的渗流速度；J为围堰裂缝处水力坡降；g为重力加速度。

在相同的渗透系数下，根据达西定理，混凝土楔形体在围堰中表现出的流量数值va就可计算为：

(2)

式中：k为渗透系数。

将上述两项渗透计算公式联立，得到混凝土楔形体运用后的渗透系数表达式：

(3)

式中：各个参数含义不变。

在上述渗透参数的控制下，选用不同水电站过流围堰的参数，见表1。

在表1所示的各项参数下，将导流围堰按照实体单元处理，以式(3)的渗透系数为参考，构建导流围堰局部的数值模型坐标系，见图1。

表1 不同水电站过流围堰的参数

图1 数值模型坐标系

以图1所示的数值模型为研究对象，导入表1中的各项系数至数值模型坐标中，模拟不同控制混凝土楔形体的开裂缝数值大小，汇总不同缝宽数值下产生的裂缝数量，见表2。

表2 模型不同缝宽产生的裂缝数量

由表2所示的数值可知，在不同缝宽数值下，裂缝数量基本可以维持在数值6及以下[4]。以表2中最大缝长及缝宽数值为自变量，构建开裂优化方程，开裂优化方程可表示为：

(4)

其中：L为裂缝长度；D为开裂深度；a为混凝土楔形体的强度；c为混凝土楔形体水泥含量。

按照上述计算公式优化导流围堰开裂特征参数，降低裂缝对围堰稳定性的破坏[5]。对开裂参数优化后，控制围堰导流过程的渗透量，最终计算得到混凝土楔形体在水电站稳定优化中的稳定系数[6]。

1.2 减少导流渗透量

采用上述优化后的开裂特征参数，在图1的模型中，计算过流水体的压力水头数值，计算公式可表示为：

(5)

其中：h为围堰的水体高度；c为围堰水体的流量参数；s为围堰的横截面积；其余参数含义保持不变。

过流围堰不同数值的开裂缝宽有着不同的压力水头[7]，假设围堰堰体分边界水头分布存在两种边界，数量关系可表示为：

(6)

式中：x,y,z均为分界位置数值；κ为分边界；t为导流时间；φ为分布函数；其余参数含义不变。

当过流围堰出现隔水边界时，式(6)中q=0，水压的各向渗透系数相等[8]，此时水体的压力水头数值就是z。但在实际水电站导流围堰中，还常常包含流量边界，此时流量边界就可表示为：

(7)

式中：f为流量；其余参数含义不变。

结合上述得到的边界数量关系，得到导流围堰的压力水头等值线，见图2。

图2 压力水头等值线

以图2所示的压力水头等值线相等的数值为相同的水流流向，在相同水流方向上，采用摩尔-库伦模型分析相同水流方向导流在围堰产生的渗透量[9]，在混凝土楔形体的参与下，计算渗透量的主应变增量，数量公式可表示为：

(8)

式中：e为混凝土楔形体产生的弹性；p为塑性应变；ε为形变参数。

根据广义的胡克定律，计算该部分水压在不同方向产生的应变增量，计算公式可表示为：

(9)

式中：σ为增量数值；下角标1,2,3分别为模型的不同坐标方向；α1、α2分别为弹性系数，存在如下数量关系：

(10)

式中：K为上下游水头差；G为水体渗透速度。

在使用混凝土楔形体稳定优化过流围堰时，当混凝土楔形体的剪应力达到临界值时，稳定优化过程会进入屈服状态[10]，该状态可表示为：

|τn|=g(σn)

(11)

上述数量关系中，混凝土楔形体在实际应用时，可根据不同状态的临界值，控制不同屈服状态[11]，进而控制水体的导流渗透量，维持围堰的稳定。

1.3 优化稳定系数

在应用混凝土楔形体后，以上述计算得到的开裂系数与渗透量数值为基础，将此时稳定优化过程视为折线型实用堰计算，计算得到堰上头水H。计算公式可表示为：

(12)

其中：γ为淹没系数；m0为流量系数；B为河道宽度；Q为单位流量。

在该数量值的控制下，长时间的水流冲击会在围堰处形成冲击坑[12]，混凝土楔形体会在围堰下游形成一个稳定消力池，稳定过程可表示为：

(13)

其中：q为水头损失；h为围堰首端水深；d为混凝土楔形体半径；y为水体的流经距离；s为水体流经时间。

根据上述计算处理公式，在混凝土楔形体的参与下，控制得到不同稳定系数[13]，围堰的稳定性系数变化见图3。

图3 稳定性系数变化

由图3所示的稳定性系数变化规律可知，随着混凝土楔形体控制得到的流速数值不断增大[14]，稳定性数值也就越小。在实际使用混凝土楔形体稳定优化水电站导流围堰时，引入一个动能校正系数[15]，进而控制围堰水流的速度，将水电站的围堰划分为不同的区段，计算不同区段的消能率。计算公式可表示为：

(14)

其中：E1为一区段的消能率；E2为二区段的消能率；E0为总区段的消能率。

在实际优化时，从水电站的下游河道开始，逐级向导流围堰的上游计算，最终完成对稳定系数的优化。综合上述处理，最终完成研究分析。

2 实 验

2.1 实验准备

实验采用混凝土原材料制成3种不同的混凝土楔形体用于实验，混凝土的配比情况见表3。

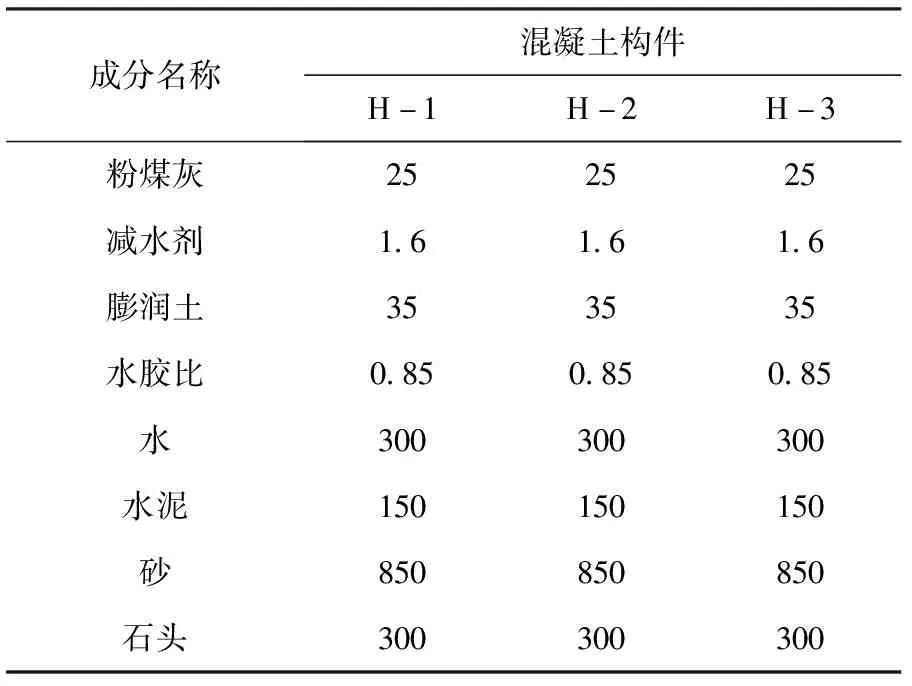
表3 混凝土含量配比

如表3所示的配比制成3种相同配比的混凝土楔形体，计算混凝土楔形体在实际使用时的各项性能参数。性能参数见表4。

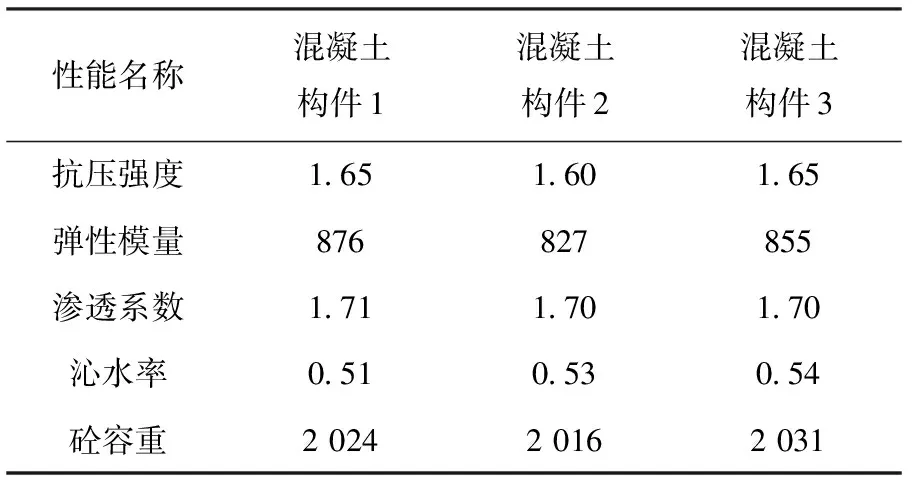
表4 混凝土构件性能参数

在上述性能参数的控制下，采用图4所示的围堰布置结构进行实验。

图4 导流围堰布置结构

在图4所示的围堰布置结构中，控制围堰堰体的水流速度维持在0.5 m/s的上升速度，计算未使用混凝土楔形体前围堰的稳定性系数，并使用一种传统应用方法与文中研究的应用方法进行对比，对比3种应用方式的性能。

2.2 结果及分析

基于上述实验准备，设定水电站内的水流速度为0.5 m/s上升方向，实验时间为50 h，设定开裂测量时间点每隔5 h测量一次，以围堰堰体的开裂数值为对比标准，在不同应用条件下，围堰的开裂数值结果见表5。

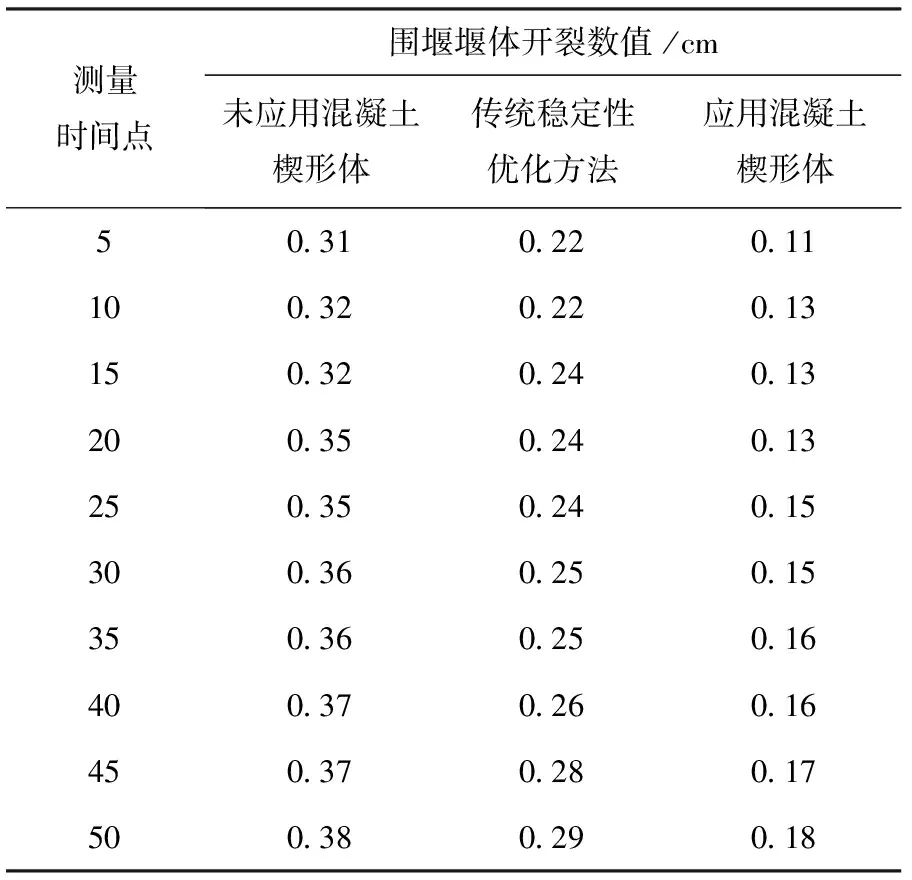
表5 围堰堰体开裂数值

由表5所示的围堰堰体开裂数值可知，3种不同的应用条件对围堰堰体有着不同程度的剪切力，不同的剪切力形成不同的开裂数值。未使用混凝土楔形体行稳定性优化方法形成的开裂数值较大，在最终测量时间点形成的开裂系数为0.38 cm，开裂数值最大；采用传统稳定性优化方法的围堰堰体最终形成的开裂数值为0.29，开裂数值较小；而文中应用了混凝土楔形体的稳定优化方法最终形成的开裂数值为0.18。综合上述对开裂数值的研究可知，应用了混凝土楔形体的稳定性优化方法能够有效地控制围堰堰体的开裂系数。

保持上述实验环境不变，在3种不同的稳定性优化条件下，采用瑞典圆弧法计算围堰的安全性系数，计算公式如下：

(15)

其中：F为安全系数；MR为抗滑力矩；Ms为土体绕圆心下滑的滑动力矩。

根据上述计算公式，取应用3种不同性能系数的混凝土楔形体的平均值作为最终的稳定性系数，最终得到3种应用条件下的稳定性数值。稳定性数值结果见图5。

图5 安全系数变化

由图5所示的安全系数变化可知，在直接对水电站导流围堰稳定性进行优化时，水电站导流围堰的安全系数在1.9左右，安全系数数值最小；在应用传统稳定优化方法时，计算得到的安全系数在2.1左右，要比稳定性优化时未使用混凝土楔形体时的安全性数值要大；而稳定优化过程中应用了混凝土楔形体的应用方法最终得到的平均安全数值为2.3左右，综合上述安全数值，文中研究的应用方法得到的围堰安全数值更大。

3 结 语

水电站导流围堰的稳定是水电站正常发电工作的重要前提，混凝土楔形体在围堰过程中能够起到稳固围堰稳定性的作用，为此研究混凝土楔形体在水电站导流围堰稳定优化中的应用。利用混凝土楔形体来优化围堰的稳定性，能够改善传统稳定性优化方法开裂数值过大、围堰安全数值过低的不足，具有一定的实用性。