基于SVM-NSGA Ⅱ的耐久性混凝土配合比多目标优化

刘富成，邓婷婷，王成龙，吴贤国，王洪涛，高 飞，黄汉洋

(1.湖北交投十巫高速公路有限公司，湖北 十堰 442000；2.华中科技大学 土木与水利工程学院，湖北 武汉 430074；3.中建三局集团有限公司，湖北 武汉 430064；4.中建商品混凝土公司，湖北 武汉 430070)

提高混凝土耐久性是延长建筑使用寿命的主要手段之一，近些年来，混凝土耐久性不足造成了大量混凝土结构破坏事故，为了减少建筑安全事故的发生，混凝土耐久性问题引来了越来越多国内外学者的关注。由于抗冻性、抗渗性是反映混凝土早期耐久性的重要指标，因此在研究混凝土配合比优化问题中，考虑抗冻性、抗渗性很有必要。又因为控制混凝土经济成本一直是工程项目的重要目标之一，因此，研究不同配合比下，综合考虑混凝土的耐久性问题和成本问题是十分有价值的。

近年来，国内外学者基于原材料配合比对混凝土耐久性问题的研究主要集中在预测和优化问题方面。在基于配合比对混凝土耐久性预测的研究中，王丽学等[1]对不同配合比混凝土试件进行冻融试验并预测，发现水灰比越大混凝土损伤越大；王露等[2]用三元一次回归预测水泥强度，发现矿渣水泥掺量越多，后期强度增长越快；冯忠居等[3]建立GM(1,1)预测模型，研究了不同配合比掺合料对混凝土耐久性的影响；Amini等[4]提出统计单变量和多变量回归模型，进行逐步回归分析，验证混凝土耐久性能；Behforouz等[5]使用人工神经网络(Artificial Neural Network，ANN)对混凝土耐久性进行预测，验证了ANN在预测这类混凝土耐久性方面有较高的准确性。在基于配合比对混凝土耐久性优化的研究中，哈娜[6]利用数学模型，采用梯形模糊数确定指标权重，优化混凝土配合比；李肖[7]利用功效函数法优化混凝土的成本系数和功能系数，筛选出耐久性最佳的配合比方案；毕继红等[8]以胶凝用量、矿物掺料种类及掺量对配合比优化并发现优化后混凝土水泥石为致密状态；蒋正武等[9]采用正交试验设计方案，利用客观权重赋予法确定了各权值，获得了最佳配合比；Shafiq等[10]用方差分析ANOVA(Analysis of Variance)技术对混凝土中纳米二氧化硅和偏高岭土含量进行优化，以获得最小氯离子渗透值。

以上研究均对提高混凝土耐久性提供了参考，但是以往研究一方面主要是针对混凝土耐久性进行预测，配合比优化研究主要是利用正交试验和经验公式，难以实现快速准确地确定配合比优化方案。因此，本文提出一种SVM-NSGAⅡ智能算法，首先以相对动弹性模量和氯离子渗透系数作为耐久性评价指标，基于混凝土原材料和配合比样本数据采用SVM(Support Vector Machines)模型对耐久性指标进行模拟得到其非线性关系函数；然后将两个函数作为NSGAⅡ(Nondominated Sorting Genetic Algorithm Ⅱ)算法的适应度函数作为两个优化目标，同时以混凝土成本函数作为另外的优化目标，进行配合比多目标优化，达到优化混凝土配合比以及经济成本的目的。

1 理论基础

1.1 支持向量机基本原理

支持向量机(SVM)作为一种智能算法，可以很好地克服非线性问题，具有全局性且适用于小样本[11]。本研究利用支持向量机预测混凝土耐久性，即是利用核函数学习输入指标与输出指标之间的规律进而做出决策的过程。

设定一组样本集T，样本内输入因素(自变量)xi和输出因素(因变量)yi呈线性函数关系。

T={(x1,y1),(x2,y2),…,(xn,yn)}

(1)

可假设这种线性函数关系为：

f(x)=WTx+b

(2)

式中：WT为权重系数向量；b为对xi赋予权重乘积后所发生的偏置数。

引入拉格朗日(Lagrange)函数，再用非线性映射函数φ(x)将非线性关系数据中的输入输出变量(xi,yi)映射到高维特征空间中，利用核函数在高维特征空间建立线性回归模型。当K(xi,xj)=φ(xi)φ(xj)时，优化问题为：

(3)

式中：α，α*为Lagrange乘数；C为其惩罚系数；K(xi,xj)为核函数，此时便可求得非线性支持向量回归机的函数表达式为：

(4)

1.2 NSGAⅡ算法基本原理

2002年，Deb等[12]为提升遗传算法的性能，对NSGA进行改进，得到带精英策略的非支配排序遗传算法(NSGAⅡ)。NSGAⅡ很大程度上降低了计算的复杂程度、拓宽了采样空间[13]。

NSGAⅡ算法最核心的特点是快速非支配排序、拥挤距离及精英策略。其中NSGA的非支配排序为O(MN3)(M为目标数，N为种群大小)，改进后非支配排序O(MN2)，从而提升了排序的速度。拥挤距离法采用了拥挤度和拥挤度比较算子计算每个解的距离。第i个解的拥挤距离计算如下：

(5)

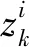
NSGAⅡ算法引入了精英策略，扩大了采样空间，避免了最佳个体的丢失，提高了算法的运算速度和鲁棒性。

1.3 基于SVM-NSGAⅡ算法的多目标优化模型构建

现实生活中，很多输入变量和输出结果之间是高度非线性的关系，为了获取两者之间具体函数形式，可以利用支持向量机模型替代传统的数学函数。同时可将支持向量机模型作为遗传算法适应度函数，实现更为精确的优化。SVM-NSGAⅡ算法的具体流程如图1所示。

图1 基于SVM与多目标遗传算法配合比优化流程

1.3.1 基于SVM混凝土耐久性预测

Step1：数据获取及预处理

根据实际工程情况，通过查阅大量文献，以常见重要的混凝土配合比参数作为混凝土耐久性预测输入参数。将相对动弹性模量和氯离子渗透系数作为预测输入参数。

数据预处理主要是对数据进行归一化，避免样本出现数据过大或过小的情况，导致数据被淹没或不收敛[14]。本文将输入变量和输出统一到[-1,1]区间，实现数据归一化，使得每个特征在预测过程中起到效果。

Step2：核函数参数优化

核函数对支持向量机预测精度有很大的影响。在不同预测模型中，应根据研究特点选择合适的核函数[15]。由于高斯核函数既有径向基核函数的优势，还有良好的抗干扰能力，本文将采用高斯核函数当作预测模型的核函数进行研究，其表达式为：

(6)

式中：xi为输入变量；x为输出变量。

在确定核函数后，为了确保支持向量机的泛化水平，本文将采用K折交叉验证，进行网格搜索对核函数宽度参数g和惩罚系数C进行优化。其中，网格搜索法是一种全局搜索法，在避免局部最优的同时节约时间[16]；K折交叉验证常用于支持向量机模型性能的验证[17]，主要作用是避免支持向量机模型欠学习或过学习状态。

Step3：预测结果分析

为了验证SVM模型的预测精度，通过两个模型性能的指标均方根误差RMSE和拟合优度R2来进行检验。均方根误差RMSE体现预测值与真实值的离散程度，拟合优度R2用于验证预测值与真实值之间的拟合程度，两个指标分别由公式(7)(8)得出。

(7)

(8)

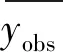
1.3.2 NSGAⅡ多目标优化

Step1：建立目标函数

(1)基于SVM的混凝土耐久性目标函数

引入SVM混凝土耐久性回归预测算法替代传统数学函数作为多目标遗传算法中的目标函数，可以很好地解决输入变量与输出目标之间存在复杂非线性关系，无法给出具体函数表达式的问题。

混凝土抗冻性回归函数maxf1和混凝土抗冻性回归函数minf2分别表示为：

maxf1(svm(x1,x2,…,xn))

(9)

minf2(svm(x1,x2,…,xn))

(10)

式中：xi为混凝土组成成分。

(2)混凝土经济成本函数

建筑施工工程中，除了应该考虑混凝土耐久性之外，成本也是不可忽视的目标之一，经济成本minf3目标函数表达式为：

(11)

式中：vi为各个混凝土组成成分的单位质量成本价。

Step2：建立目标约束范围

为了使得生成的方案更加合理可行，需要对方案生成时的各个因素设定限制范围，形成变量的约束条件，约束条件的一般形式为：

bil

(12)

式中：xi为第i个设计参数；bil和biu分别为第i个设计参数值的下限和上限。

Step3：NSGAⅡ多目标优化

当目标函数和约束条件都确定下来之后，便可基于NSGAⅡ算法实现多个目标优化，可以找到基于配合比参数的混凝土耐久性的Pareto最优解集。与传统GA相比，NSGAⅡ算法的关键步骤主要有两个：

(1)在设置初始种群后，NSGAⅡ算法将通过快速非支配排序后，利用三个遗传机制获得首批子代种群。

(2)第二代种群将父、子代合并，再一次通过快速非支配排序，计算个体之间拥挤距离之后，按步骤(1)再次产生新的子代种群。

2 基于SVM-NSGAⅡ算法的混凝土耐久性多目标优化

2.1 工程项目

我国东北高寒高盐碱地区某高速公路项目，对混凝土耐久性有比较高的要求。因此，本文基于该高速公路项目获取混凝土配合比试验数据及相对动弹性模量和氯离子渗透系数的数据样本(其中相对动弹性模量为经过300次冻融循环后的相对动弹性模量，氯离子渗透系数为28 d氯离子渗透系数)，以C50混凝土为研究对象研究混凝土耐久性。实验中所用到的水泥是吉林亚泰天鹅牌P·O52.5水泥，产地是黑龙江省安达市；所用到的粉煤灰是国电双辽I级粉煤灰；所采用的高效减水剂来自于中交武汉港湾工程设计研究院有限公司。

2.2 基于SVM的混凝土耐久性预测

2.2.1 数据获取与预处理

本文从混凝土配合比层面来研究其对混凝土耐久性的影响，选取相对动弹性模量和氯离子渗透系数作为SVM预测模型的输出指标。通过查阅大量文献和工程实况，将水胶比、水泥用量、砂子用量、石子用量、粉煤灰用量、减水剂用量，膨胀剂用量和硅灰用量作为输入特征指标。通过现场实验，基于正交试验设计了36组，为了保证SVM预测模型的预测效果更加精准，以正交试验为基础，将实验数据集扩充到100组，样本数据如表1所示，从全部样本随机抽取80组样本构成训练集，剩下的20组样本作为测试集。对输入和输出特征指标进行归一化处理。

表1 输入和输出指标样本数据

2.2.2 核函数参数优化

根据1.3节的分析，选择5折交叉验证法和网格搜索法对SVM模型的核函数宽度参数g和惩罚系数C进行选优，分别得到相对动弹性模量和氯离子渗透系数核函数最优参数，图2，3分别为相对动弹性模量、氯离子渗透系数预测参数优化结果3D视图。

图2 相对动弹性模量参数优化3D视图

从图2中可知，惩罚系数bestC=16，核函数参数bestg=0.035897，此时均方根误差CVmse=0.0019962。表示C=16，g=0.035897，在5-CV验证后的均方误差值最小。

同样，从图3中可知，惩罚系数bestC=27.8576，核函数参数bestg=0.57435，此时均方根误差CVmse=0.0023188。表示C=27.8576，g=0.57435，在5-CV验证后的均方误差值最小。

图3 氯离子渗透系数参数优化3D视图

2.2.3 预测结果分析

基于SVM核函数参数优化的结果，利用训练集进行学习模拟，分别建立SVM相对动弹性模量预测模型和氯离子渗透系数预测模型，再利用测试集对训练集的预测模型进行检验。根据上述步骤，相对动弹性模量训练集预测结果如图4a，测试集预测结果如图4b；同理氯离子渗透系数训练集预测结果如图5a，测试集预测结果如图5b。

图4 相对动弹性模量预测结果

图5 氯离子渗透系数预测结果

从图4能够发现，SVM模型能够很好地预测相对动弹性模量的变化。图4a为相对动弹性模量训练集预测模型，均方根误差为0.071，拟合优度为0.97192，可以看出该模型拟合结果很好，其预测值与实际值之间误差非常小。图4b为SVM模型对训练集预测回归函数的检验，其中均方根误差为0.066，拟合优度为0.96686，混凝土抗冻性的支持向量机预测模型对测试集样本的预测值与试验值吻合的非常好。以上可以说明该模型对相对动弹性模量预测具有良好的效果且具有较好的泛化能力。

同理可得，从图5中可以看出SVM预测模型对氯离子渗透系数预测同样具有良好的效果。

2.3 基于SVM-NSGAⅡ算法混凝土耐久性多目标优化

2.3.1 建立目标函数

在实际工程项目中，为了确保混凝土耐久性可以满足建筑使用安全标准，一般都会采用性能良好、质量较优的原材料，但是这往往会增加混凝土的经济成本，因此，为了在保证项目中混凝土耐久性的同时，尽可能降低混凝土的经济成本，本文将以混凝土耐久性和经济成本为目标进行多目标优化。

(1)基于SVM的混凝土抗冻性目标函数

混凝土的抗冻性将用相对动弹性模量来衡量，根据式(9)可得混凝土抗冻性目标函数maxf1：

maxf1(svm(x1,x2,…,x8))

式中：x1～x8分别为水胶比、水泥用量、粉煤灰用量、砂子用量、石子用量、减水剂用量、膨胀剂用量、硅灰用量。

(2)基于SVM混凝土抗渗性目标函数

混凝土的抗冻性将用氯离子渗透系数来衡量，根据式(10)可得混凝土抗渗性目标函数minf2：

minf2(svm(x1,x2,…,x8))

(3)混凝土经济成本函数

建筑施工工程中，除了应该考虑混凝土耐久性之外，成本也是不可忽视的目标之一，根据工程实际情况获得混凝土原料价格：水泥单价为0.37元/kg、水的单价为0.002元/kg、砂的单价为0.105 元/kg、石的单价为0.102元/kg、粉煤灰单价为0.38元/kg、减水剂的单价为4.65 元/kg，膨胀剂的单价为7.1元/kg，硅灰的单价为1.25 元/kg。根据式(11)可得经济成本目标函数minf3：

minf3=0.37x2+0.002x1(x2+x3+x8)+0.38x3+

0.105x4+0.102x5+4.65x6+7.1x7+1.25x8

2.3.2 建立多目标约束范围

本文选择P·O52.5水泥，加入适量的粉煤灰改善混凝土的强度、耐久性，加入高效减水剂增强混凝土和易性。根据规范以及工程实际等要求确定合理的配合比参数取值范围，其中水胶比为0.28～0.4，水泥用量为330～450 kg·m-3，粉煤灰用量为56～98 kg·m-3，砂用量为620～860 kg·m-3，石用量为1030～1155 kg·m-3，减水剂的含量为0.5%～1.6%，膨胀剂的含量为0.5%～1.2%，硅灰的含量为18～28 kg·m-3，同时考虑规范对混凝土施工配制强度要求，根据式(12)确定配合比优化的约束条件：

式中：fcu,k为混凝土立方体抗压强度标准值。

2.3.3 基于NSGAⅡ的多目标优化

在混凝土耐久性和经济成本的目标函数以及混凝土配合比约束范围后，基于NSGAⅡ进行多目标优化。本文取NSGAⅡ算法的交叉算子为0.7，变异算子为0.01，种群大小为40，最大进化代数和停止代数为60，以混凝土耐久性和经济成本为目标，利用NSGAⅡ算法进行全局寻优，迭代60次后得到最优配比组合，如图6所示，计算得到满足条件的40组优化结果如表2所示。

图6 多目标最优配合比组合

从图6中可以看出，随着相对动弹性模量的增加以及氯离子渗透系数的降低，混凝土的经济成本呈上升趋势；同时随着氯离子渗透系数的降低，相对动弹性模量也在不断减少。其中氯离子渗透系数在1.5～3 cm2/s之间取值，相对动弹性模量在92%～98%之间取值，混凝土经济成本函数在390～430元之间取值。

由于项目处于高寒高盐碱环境，项目对混凝土耐久性要求比较高，其中混凝土经过300次冻融循环后相对动弹性模量在95%以上，28 d氯离子渗透系数在2.5×10-8cm2/s以下，混凝土耐久性才可以达到项目耐久性的目标。从表2中可以看出，当相对动弹性模量和氯离子渗透系数均达到目标耐久性要求时，最低的混凝土经济成本为399.84元，此时单位体积混凝土水胶比为0.306，水泥用量为394.26 kg，砂用量为808.1 kg，石用量为1068.07 kg，粉煤灰用量为63.33 kg，硅灰用量为3.78 kg，减水剂用量为1.67%，膨胀剂用量为3.29%。

表2 三目标优化结果对应的配比参数取值

3 结 论

(1)本文建立一种基于SVM-NSGAⅡ多目标优化模型，首先利用SVM对混凝土耐久性主要指标相对动弹性模量和氯离子渗透系数实现高精度预测，在此基础上根据项目实际条件，将以上混凝土耐久性指标的预测回归函数作为适应度函数，以混凝土经济成本函数为另一个适应度函数，结合规范及工程项目的要求建立原材料及配合比相关的约束条件，利用NSGAⅡ算法进行多目标优化，得到最优配合比。

(2)选取水泥用量、砂用量、粉煤灰用量、水胶比等8个因素作为最优输入变量集构建基于SVM预测混凝土抗冻性和抗渗性模型，预测结果表明采用SVM算法对混凝土抗冻性和抗渗性进行预测的精度很高。其中，在对混凝土抗冻性进行预测时，均方根误差为0.066，拟合优度为0.96686；在对混凝土抗渗性进行预测时，均方根误差为0.081，拟合优度为0.97599。说明了SVM模型在混凝土耐久性预测中的可行性以及有效性。

(3)结合规范和项目实际要求，以混凝土经济成本函数作为目标适应度函数之一，同时将混凝土抗冻性和抗渗性SVM回归预测函数作为另外两个目标适应度函数，进行NSGAⅡ多目标优化后，相对动弹性模量、氯离子渗透系数以及混凝土经济成本分别为95.1056%，2.46643×10-8cm2/s，399.84元，得到混凝土抗冻和抗渗性优良且材料成本最低的配合比组成，通过实验其强度、工作性能以及耐久性能指标均符合工程实际要求。结果表明，该方法是一种智能、精确、高效的配合比优化方法，在工程生产中具有非常好的应用价值，对工程实践具有一定的指导作用。