剪切膜单元用于模拟内填钢筋混凝土墙板的可行性分析
2021-01-06王沁心王华飞
王沁心,顾 强,齐 益,王华飞
(1.苏州科技大学 土木工程学院,江苏 苏州215011;2.河海大学 土木与交通学院,江苏 南京210098)
钢框架内填钢筋混凝土剪力墙(SRCW)结构是在钢框架中填充钢筋混凝土墙板作为结构抗侧力体系,混凝土墙板一般通过抗剪连接件与钢框架组合,承受水平力,其具有较好的侧向强度、刚度、延性和经济性。
对大型钢框架内填钢筋混凝土剪力墙结构进行内力分析时,采用精细的有限元划分往往由于所需内存和机时过大而难以实现,寻求内填墙板的简化分析模型具有实际意义。
国内外已对钢框架内填钢筋混凝土剪力墙结构的内力简化分析方法做了很多的试验和研究[1-7],2018年中国标准设计研究院牵头编制完成的《钢框架内填墙板结构技术规程(征求意见稿)》第5.3.2条提出,钢框架内填墙板在分析模型中不宜承受竖向荷载,主要承担水平荷载。在建模分析时,将正常的各向同性的墙板拉压刚度乘以0.1系数进行折减,而剪切刚度保持不变。也可以采用纯剪切单元。
本文对用剪切膜单元模拟墙板的适用性进行了研究,比较了用剪切膜单元和平面应力单元模拟墙板时,SRCW结构弹性内力分析结果产生的差异。评估了使用剪切膜单元模拟墙板的可行性。
1 有限元模型
1.1 钢材本构
有限元模型的钢柱、钢梁选用Q355B钢,弹性模量ES=206 GPa,钢材泊松比为0.28。
1.2 混凝土本构
(1)平面应力单元。使用ANSYS时,内填钢筋混凝土墙板采用整体式模型,假设钢筋弥散在混凝土中,利用配筋率及剪切模量折减系数修改单元刚度矩阵的物理矩阵,得到适用于主要承担水平荷载的剪力墙材料本构。
普通平面应力单元采用的物理矩阵是

本文用于混凝土剪力墙板时,根据《钢框架内填墙板结构技术规程(征求意见稿)》第5.3.2节对物理矩阵进行如下修正

式中,Ec'=Ec/(1-μc2),Ec为混凝土的弹性模量;Gc=Ec/[2(1-μc)];μc=0.2。矩阵中的0.1系数是考虑开裂及避免墙板承担较大竖向荷载对混凝土拉压刚度的折减,Ku=0.4是考虑混凝土开裂对抗剪刚度的折减。
参考文献[8]推导的钢筋物理矩阵及整体式钢筋混凝土剪力墙模型物理矩阵,平面应力单元弥散钢筋的物理矩阵为

式中,Es为钢筋的弹性模量;ρsx、ρsy分别为内填墙沿x轴、y轴的配筋率。
将式(2)和(3)相加,即可得到配筋的混凝土墙板平面应力单元的物理矩阵式(4)。
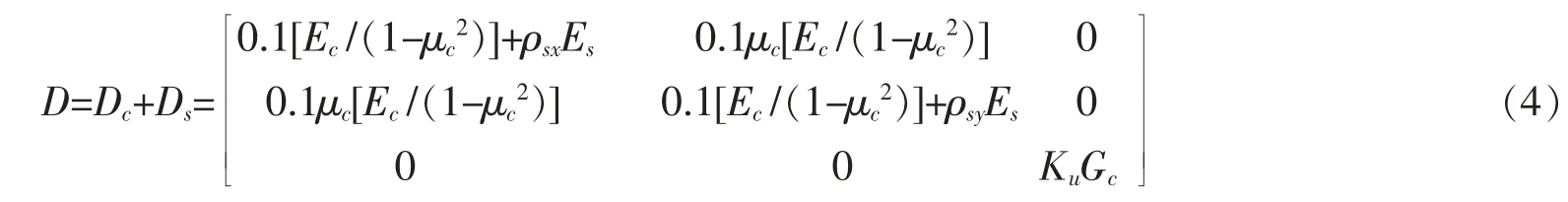
由式(4)可看出钢筋混凝土墙板平面应力单元建模时采用的弹性剪切模量为

(2)剪切膜单元。与平面应力单元相比,剪切膜单元只有弹性剪切模量这一个参数,故其不能反映墙板配筋的影响。其应用时只需填写弹性剪切模量,即按式(5)折减的剪切模量。剪切膜单元为矩形四节点平面单元,节点位于四个角点,每个节点有两个自由度,剪切膜单元只承受剪力,单元四个角点必须与其他有轴向刚度和抗弯刚度的单元节点相连,且一层墙板只划分为一个单元,可有效节约计算机内存及机时。
2 单元设计
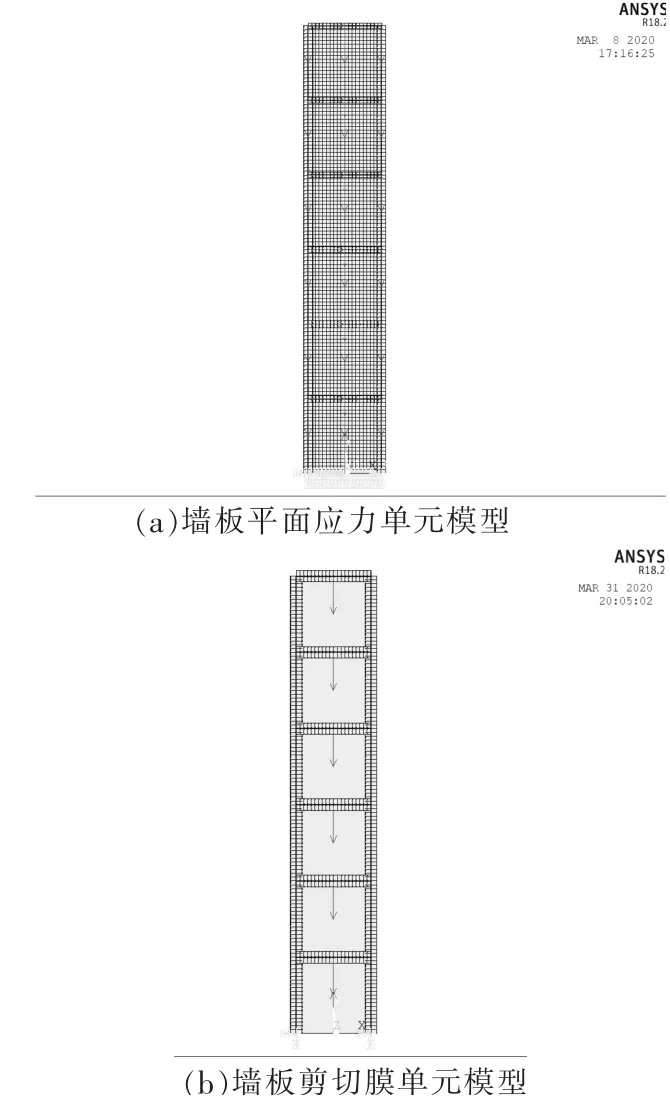
图1 单元类型
单元划分见图1。钢柱钢梁均采用beam188单元;钢筋混凝土墙板分别采用plane42单元和shell28单元。本文主要研究目的是墙板的内力分析模型,对抗剪连接件不做研究,假定抗剪连接件能可靠传递钢框架与钢筋混凝土墙板间的相互作用,连接件不破坏,将内填墙与梁柱绑接,即梁柱与墙板连接处的点(NODE)具有相同的位移。
结构底部与地面固接,在plane42单元模型中约束底部各点的所有自由度,在shell28单元模型中约束框架柱脚的所有自由度。
3 BASE算例设计

图2 结构平面布置图
结构平面布置见图2。设计一个6层钢框架内填钢筋混凝土剪力墙结构算例BASE。层高3.3 m,边跨6.6 m,中跨3.3 m。结构抗震设防烈度为7度(0.15g),设计地震分组第一组,场地类别Ⅱ类。墙板混凝土强度等级C25,钢材选用Q355B。该结构抗侧力体系由钢框架内填钢筋混凝土剪力墙组成,承担全部水平荷载,其他框架结构仅承担竖向荷载。竖向荷载根据《建筑结构荷载规范》(GB50009-2012)[9]取值,水平地震作用根据底部剪力法计算。
经设计后,框架柱截面1至6层均为H型钢500 mm×500 mm×24 mm×26 mm,框架梁截面1至2层为H型钢400 mm×300 mm×16 mm×18 mm,3至6层为H型钢400 mm×250 mm×14 mm×18 mm。剪力墙厚度第1至6层分别为280 mm、260 mm、240 mm、200 mm、140 mm和140 mm,钢筋为HPB335,配筋率1至6层分别为0.538%、0.579%、0.628%、0.754%、0.748%和0.748%。
用ANSYS软件进行弹性内力分析比较的平面结构为图2计算榀的中间带墙跨,采用前文所述材料本构,施加的荷载组合为1.2倍的重力荷载代表值与1.3倍的水平地震作用之和。
4 BASE算例计算结果对比分析
4.1 层间位移
图3 及图4为plane42和shell28单元模型的结构变形图,结构变形形状与裸钢框架受水平荷载作用时表现出的剪切变形形状不同。剪力墙板有增大结构抗侧刚度的作用,结构变形表现出弯曲变形的特征,plane42单元和shell28单元都很好地模拟了这种特征。略有差别的是,使用剪切膜单元计算出的结构位移略微偏大,可能是由于剪切膜单元无法考虑钢筋的影响,不能完全模拟出钢筋混凝土剪力墙的抗侧刚度所致。
表1 为BASE算例两个模型的层间位移角对比。可以看出,shell28与plane42模型模拟的层间位移角基本相似,最大层间位移角均出现在第5层,shell28模型与plane42模型模拟的层间位移角差异随层数增加而增大。Plane42作为最常用的平面应力模拟单元,其精度是可信的,故认为shell28单元模型随结构层数增加层侧移误差增大。虽然两个模型计算的水平位移略有差别,但差异较小,可以认为shell28单元在计算结构的水平位移时替代效果较好。

图3 plane42单元结构变形图

图4 shell28单元结构变形图

表1 BASE算例两模型层间位移角对比
4.2 剪应力云图对比
图5 及图6所示为两个模型的剪应力云图,钢框架柱中剪应力十分微小,而剪力墙中剪应力较大。Plane42单元的剪力墙中剪应力从第1层到第6层呈现递减的趋势,且在每一层墙板对角带状区域的剪应力较大。而shell28模型与plane42模型计算结果不同,在用剪切膜单元模拟剪力墙时,一块墙板为一个单元虽然可大大减少计算机内存和机时,但计算精度显得粗糙。在结构的第1层到第5层,墙板剪应力都表现出没有太大差别,其中第5层显示出有轻微变化。另外分析单独一块墙板可以发现,shell28单元因无法划分多个网格的缘故,不能像plane42单元那样能表现出剪力墙对角线受力的特征,也就是说其剪应力分布平均。
可以认为在研究结构的剪应力分布时,shell28单元的替代性较差。

图5 plane42单元剪应力云图(单位:N/mm2)
4.3 竖向荷载分担对比
图7 和图8分别为两个模型的框架轴力图,由于水平荷载产生的倾覆力矩较大,两柱轴力为一拉一压。从框架轴力的分布来看由于shell28与梁柱交点相连,故框架柱的轴力不像plane42单元模型那样呈线性分布,而是分段式均匀分布。
表2 为两个模型框架柱及剪力墙分担竖向荷载的占比,其中剪力墙承担的竖向荷载通过各层剪力墙底部在Y方向上的应力对横截面积分而来,该值与各层框架柱底部轴力代数和等于总竖向荷载。由表2可以发现,在plane42单元中,剪力墙分担竖向荷载比例为9.4%~17.3%,随层数的增加呈减小趋势,证明当竖向荷载较大的时候,剪力墙会分担较大比例的竖向荷载。框架柱承担的竖向荷载比例为82.7%~90.7%,虽然变化略大,但总体上来说框架柱仍然保持其分担大部分竖向荷载的性质。而在shell28单元模型中,由于shell28单元不能受竖向荷载作用,故框架柱承担了全部的竖向荷载,这与实际情况不符。
可以认为,在研究竖向荷载占比时,shell28单元的替代效果较差。

图7 plane42单元框架轴力图(单位:N)

图8 shell28单元框架轴力图(单位:N)

表2 框架柱及剪力墙分担竖向荷载占比
4.4 水平荷载分担对比
图9 及图10分别为两个模型的框架剪力图。可以看出,plane42单元模型的框架剪力与一般裸钢框架柱层间剪力不会变化不同,钢框架内填钢筋混凝土剪力墙结构每层柱受到的剪力是随高度变化的。在柱脚及梁柱节点处有较大的剪力,而在柱中剪力很小。这是由于柱和梁受到剪力墙的约束作用导致的。而shell28单元通过角点与框架相连,柱剪力分布就不像plane42单元这样随高度变化,而是同层柱剪力近似相同,更加接近裸钢框架的剪力分布形状。需要注意的是,shell28单元忽略了剪力墙和框架在角点之外位置的相互作用,是不符合实际的,应用时需注意。
表3 给出两种模型剪力墙及框架柱承担水平荷载的比例,其中剪力墙的剪力通过对剪应力积分求出,框架柱剪力为同一高度两柱截面剪力之和,plane42单元模型的框架柱剪力则是通过同层柱受到的剪力积分再除以柱高度求得的,框架柱分担剪力与剪力墙分担剪力之和等于总水平荷载。由表3可知,使用plane42单元模拟和使用shell28单元模拟时,剪力墙分担的水平荷载比例均在95%以上,且两者之间的差别十分微小。
可以认为在分析结构水平剪力时,shell28单元有良好的替代作用。

图9 plane42单元框架剪力图(单位:N)

图10 shell28单元框架剪力图(单位:N)
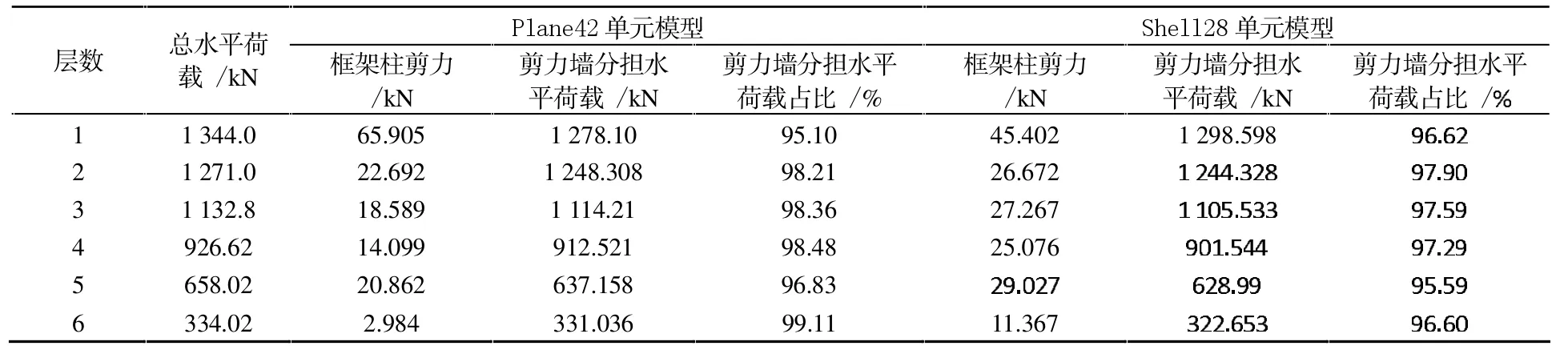
表3 框架柱及剪力墙分担水平荷载占比
4.5 倾覆力矩分担对比
表4 为两种模型框架及剪力墙倾覆力矩占比,总倾覆力矩为结构各层底部截面以上的水平各力对底部跨中的力矩。框架分担的倾覆力矩等于两柱的轴力对跨中的力矩,给出的剪力墙倾覆力矩占比为总倾覆力矩减去框架承担的倾覆力矩。由表4可知,在plane42及shell28单元模型中,框架都承担了绝大部分倾覆力矩,基本与实际相符。但不同的是,shell28中剪力墙承担了较大的倾覆力矩,且两模型剪力墙板分担的倾覆力矩占比的差异随层数增加而变大。在研究结构倾覆力矩占比时,shell28单元的替代效果一般,误差较大。

表4 框架及剪力墙分担倾覆力矩占比
4.6 框架弯矩图对比
图11 及图12为两模型的框架弯矩图,两者的弯矩分布有较大差异。Plane42单元模型的框架弯矩极值点在右柱脚,约有138 N·mm,shell28单元模型的框架弯矩极值点亦在右柱脚,但只有89.4 N·mm。这主要是因为shell28单元模型框架柱承担了更多的竖向荷载和更少的水平荷载造成的。
观察两模型弯矩分布的差别,可以发现,plane42单元模型的柱弯矩分布在柱脚较大,而后随高度增加迅速减小,而shell28单元模型的柱弯矩则近似呈线性分布。这种差异产生的原因亦是shell28单元独特的连接方式,除角点外不与框架相连的特性使得剪力墙与柱没有相互作用。
观察两模型的梁弯矩分布可以发现,在plane42单元模型中,只有梁端有较小的弯矩,这是因为plane42单元墙板对梁有较好的约束作用,对梁上荷载有较好的分担作用。而从shell28单元模型的梁弯矩分布可以发现,其分布形式更接近裸钢框架的梁弯矩分布,这是由于shell28单元不能承担竖向荷载,其与框架通过梁柱交点相连,对梁完全没有支撑作用导致的。
由此可以得出结论,对框架弯矩分布,shell28单元并没有较好的替代作用。

图11 plane42单元框架弯矩图(单位:N·mm)

图12 shell28单元框架弯矩图(单位:N·mm)
4.7 计算机时对比
表5 给出了两个模型的计算机时对比,均采用CPUTIME计时。由表5可以看出,当采用shell28单元分析单榀框架时,节约了1 s左右的机时,shell28单元模拟效率提高了29.39%。
由于本文所选用的模型较为简单,故shell28单元节省计算计时的效果不够明显,当面对大型空间结构,几十块墙板时,其节省机时的优势可以更好地发挥出来。
5 参数变化影响
经上述对比分析,可以得出剪切膜单元(shell28单元)在模拟结构的变形和墙板剪力时,具有良好的替代作用,而在其他方面则不具备较好的替代性。限于篇幅,只给出了结构层数变化和墙板宽度变化对shell28单元替代作用的影响。
5.1 层数变化的影响
将层数由6层改为12层,按第3节同样方法重新计算荷载并设计剪力墙。因本文目的是分析shell28单元的适用性,不追求设计优化,12层钢框架梁柱截面仍与6层结构相同。在重力荷载代表值和水平地震荷载组合工况下,使用两种墙板模型对结构进行模拟。
(1)层间位移对比。图13及图14为12层结构两种模型的结构变形图。可以发现两个模型仍然很好地模拟出了剪力墙对结构抗侧刚度的加强效果,但由表6可以发现随着结构层数的增加,shell28单元与plane42单元模型位移模拟结果的差异增大,即可认为shell28单元对12层结构位移的模拟效果比6层结构差。

图13 plane42单元结构变形图

图14 shell28单元结构变形图

表6 两模型层间位移角对比

图15 plane42单元框架剪力图(单位:N)

图16 shell28单元框架剪力图(单位:N)

表7 框架柱及剪力墙分担水平荷载占比
(2)水平荷载分担对比。图15及图16为12层结构两个模型的框架剪力图(表7为12层结构两个模型框架柱及剪力墙分担水平荷载的占比)。两个模型剪力的分布特征与6层结构相比没有太大改变,只是数值变化较大,但是这也导致两个模型剪力分布的差异性看起来更大了。
由表7可知,当结构为12层时,shell28单元模型的剪力墙承担了更多的水平荷载,这与6层结构略有不同。但从数值上分析两个模型的水平荷载分担比例仍极为相似,说明即使对12层结构,shell28在墙板剪力研究时仍有非常好的替代效果。
5.2 跨度变化的影响
将6层结构中间带墙榀框架跨度由3.3 m改为5.7 m,按上文同样设计方法重新计算其荷载、设计剪力墙,在同样的荷载工况组合下,使用两个墙板模型对结构弹性内力进行计算。
(1)层间位移对比。图17及图18为跨度增大时两模型的变形图,可以发现当墙板宽度增大,高跨比从1.0降低到0.579时,结构的侧向刚度大幅度提高,其侧向位移最大值降低了约57%。由此可见,在设计钢框架内填钢筋混凝土剪力墙结构时,调整带墙榀框架高跨比是改善其侧向刚度的一种着实有效方式。不同的是,使用shell28单元时,框架梁发生了较大弯曲变形,而plane42模型中没有此现象。这种现象的产生是由于梁跨度增加,而剪切膜单元只与梁柱交点连接,不能像平面应力单元那样对梁的平面内弯曲提供约束,而实际结构的内填墙板会约束梁产生较大的平面内弯曲变形。
表8 为两模型层间位移角对比,可以发现,随着墙板宽度的增加,两种墙板单元模型模拟的层间位移角差异减小了。在这种情况下,使用shell28代替plane42模拟剪力墙会有更高的精度。可以认为,当墙板宽度增加时,shell28单元在模拟结构弹性位移时有更好的替代性。

图17 plane42单元结构变形图

图18 shell28单元结构变形图

表8 模型层间位移角对比
(2)水平荷载分担比例。图19及图20为两个模型的框架剪力图,其分布特征与6层BASE算例基本相同,只是shell28单元模型梁中剪力大于柱中剪力的特征更明显了,同样是由于shell28单元不能对梁提供支承造成的。
表9 为两模型框架柱及剪力墙分担水平荷载占比。可以发现,当墙板宽度增大时,剪力墙分担的水平荷载比例较之6层BASE算例有所提高。而观察两个模型数据对比可以发现,当墙板宽度增大时,其差异也减小了,说明了在墙板宽度较大时,shell28单元有更好的替代作用。
(3)框架弯矩图对比。当高跨比改变时,两个模型的框架弯矩分布表现出了更大的差异性,分析框架弯矩图表明,shell28单元在分析结构弯矩时不具备替代性。

图19 plane42单元框架剪力图(单位:N)

图20 shell28单元框架剪力图(单位:N)

表9 框架柱及剪力墙分担水平荷载占比
图21 及图22为两模型的框架弯矩图可以发现,与plane42单元不同,框架跨度增加对shell28单元模型的框架弯矩图影响较大。由于其单元与框架只是通过梁柱交点连接,故框架梁中有较大的弯矩,远大于柱中弯矩,整个框架的弯矩图与裸钢框架只承受竖向荷载时有些类似,并且与6层BASE算例中shell28单元模型的顶层框架梁弯矩图类似,与一般的裸钢框架承担水平荷载时的弯矩图完全不同。需注意实际情况下剪力墙会对梁弯曲变形起到约束作用,不会使梁产生如此大的弯矩。故shell28单元用在跨度较大结构时,其模拟出的框架弯矩分布很不正确。

图21 plane42单元框架弯矩图(单位:N·mm)

图22 shell28单元框架弯矩图(单位:N·mm)
6 结论
(1)用简化的剪切膜单元(shell28单元)代替平面应力单元(plane42单元)模拟墙板时,墙板只划分为1个单元,可大大节省计算机内存及计算机时;
(2)与平面应力单元模型相比,采用剪切膜单元对钢框架内填钢筋混凝土剪力墙结构进行弹性分析,得出的墙板剪力误差较小,可以忽略不计;结构变形模拟结果的误差也不大;
(3)由于剪切膜单元只在梁柱的交点与框架相连,在框架平面内与梁柱单元之间相互作用,对梁柱构件不能提供面内支承,shell28单元模型模拟出的钢框架内力分布与plane42单元模型结果有较大差异;
(4)高层结构的墙板采用平面应力单元和剪切膜单元计算出的框架剪力、结构位移差异比多层结构增大;虽然从变形定性分析,两种模型都能模拟出结构特性,但从结构位移定量分析来看,对高层结构两种模型的模拟结果还是有差异的;
(5)增大钢筋混凝土墙板的宽度可以提高结构侧向刚度,在墙板宽度较大的情况下,plane42单元和shell28单元模拟结果的相似性进一步提高,此时使用shell28单元代替前者模拟钢筋混凝土墙板有较好的精度。
