一种新型煤矿底板破坏深度预测模型

武 雪 琪

（同煤集团生产技术处，山西 大同 037000）

0 引 言

煤矿底板破坏深度是评价煤矿底板突水危险和留设防水煤柱的重要依据，近些年来随着开采深度的增加，开采水平加深，开采煤层距离底板强含水层的距离不断减小，工作面受底板突水的威胁增加。因此掌握有效的底板破坏深度预测方法，对底板突水威胁进行预警，进而消除煤矿底板突水危害，保障煤矿安全生产具有重要意义[1-3]。

对于底板破坏深度预测，国内外学者进行了大量研究并取得了十分丰硕的成果。宋文军指出理论分析及经验公式这两种煤矿现场应用较多的底板破坏深度预测方法对底板破坏深度的影响因素的考虑较为单一，在应用时存在不足之处，易使预测结果与实测值偏差较大，基于此宋文军提出底板破坏深度的ANSYS WORKBENCH 的预测方法，对现场应用具有一定的指导[4]。韩进，王颖，施龙青等在大量现场底板破坏深度实测数据的基础上，提出构建GA-SVM 底板破坏深度预测模型，充分发挥该模型在小样本时适应度好的特点，并通过“留一下验证法”验证GA-SVM 预测模型的泛化度，该模型在现场具有很好的预测效果[5]。邵良杉，周玉提出在预测底板破坏深度时应该以PSO 优化输入权值和隐层阈值的ELM为预测器，以Boosting 算法为学习框架，构建底板破坏深度的PSO-ELM-Boosting 预测模型，并通过现场实践验证了该模型的有效性[6]。崔凯根据粗糙集理论，建立底板破坏深度知识表达体系，通过粗糙集规则处理数据，建立BP 神经网络底板破坏预测模型并在肥城煤田进行实践，预测结果与实际情况接近[7]。张文泉，赵凯，张贵彬等应用灰色关联度分析理论对底板破坏深度的各影响因素进行求解，并利用Matlab 软件拟合底板破坏深度公式，该研究成果完善了目前现有的底板破坏深度公式体系，预测精度较高[8]。路畅，尹立明，李杨杨等提出建立基于灰色系统理论的煤矿底板破坏深度预测模型，确定底板破坏深度的GM(0，N)模型参数，通过现场实际验证，该模型预测结果更加接近现场实际情况[9]。于小鸽，韩进，王丹丹提出可以通过模糊综合评判决策理论预测煤层底板破坏深度[10]；朱志洁，张宏伟，王春明提出可以利用ABCA 算法及SVM 模型综合研究煤层底板破坏深度问题[11]；白丽扬，赵金海，刘占新提出可以通过数据挖掘算法解决煤层底板破坏深度预测问题[12]；赵云平，邱梅，刘绪峰等构建了GRA-FOA-SVR 煤层底板破坏深度预测模型[13]；张风达通过应用多元非线性预测模型来预测煤矿深部煤层底板破坏深度[14]。

本文基于自适应权重和遗传算法的交叉、变异步骤可以解决局部最小化特性，将遗传算法与增加自适应权重的粒子群优化算法结合以解决粒子群优化算法的局部最优解问题，获得全局最优解，并将改进的GA-PSO 算法与SVM 算法相结合，构建一种新型的煤矿底板破坏深度预测模型，为煤矿底板破坏深度预测提供借鉴。

1 粒子群优化算法

粒子群优化算法是目前应用较广泛的智能优化仿生型算法，是以鸟类捕食为基础建立，以空间中多个粒子代表多个随机解，对粒子周围区域进行搜索以寻找最优解的方法，具有结构简单、易于实现等优点，且具有较强的全局搜索能力。

在n 维空间存在由m 个粒子组成的群体，用xi=(xi,1，xi,2，…，xi,m)T表示其中第i 个粒子的位置，用vi=(vi,1，vi,2，…，vi,m)T表示其中第i 个粒子的速度，用Pi=(Pi,1，Pi,2，…，Pi,m)T表示n 维空间中的最佳粒子，Pg=(Pg,1，Pg,2，…，Pg,m)T为m 个粒子中的最佳粒子，粒子群算法中粒子的速度和位置随机变化，其变化公式为（1）、（2）所示，通过不断更新粒子速度和位移公式，实现粒子从最优解偏远区域不断向最优解逼近，直至得到最优解。

式中：c1、c2为学习因子；r1、r2为介于0～1 的随机数，为k 次迭代第d 维粒子速度；为k 次迭代第d 维粒子位移；为k 次迭代第d 维单个粒子的最佳粒子位置；为k 次迭代第d 维粒子群中的最佳粒子位置。

2 SVM 基本理论

支持向量机（SVM）是建立在统计学习理论的基础上，采用结构风险最小化原则，能够很好地处理小样本、非线性问题，其形式类似神经网络，结构图如图1 所示。

图1 支持向量机结构图

式中：b 为阈值；ω 为权值矢量；θ(x)为转化过程中的非线性映射。

应用统计理论通过下列目标数极小化来确定SVM 回归函数：

然后通过拉格朗日求解方法解决上述公式表示的约束最优化问题时，可将原问题转化为对偶问题，其对偶问题表达式为：

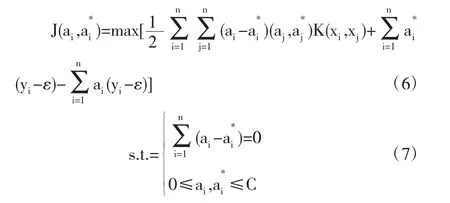
由上述表达式可求解SVM 回归方程为：

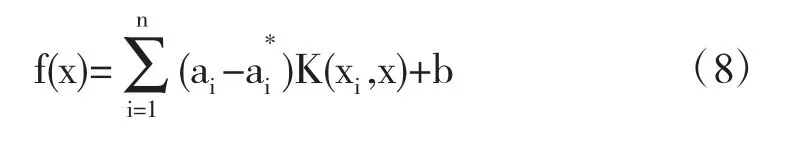
3 改进的GA-PSO-SVM 算法

3.1 粒子群优化算法增加自适应权重

粒子群优化算法中粒子的速度决定了粒子的运动方向和距离，粒子在下一时刻的位置是由粒子当前的位置与当前的速度共同确定。因此可在传统粒子群算法得粒子速度公式中引入自适应权重，自适应权重值是指粒子前期速度对当前速度的影响程度，其随粒子目标值的改变而改变，当自适应权重值较大时，粒子前期速度对当前速度的影响较大，有利于全局搜索，当自适应权重值较小时，粒子前期速度对当前速度的影响较小，有利于局部搜索，通过调节自适应权重值的大小，可以使粒子群优化算法避开局部极小值，改变粒子的速度状态，增强粒子的全局及局部搜索能力，自适应权重的计算公式如下：

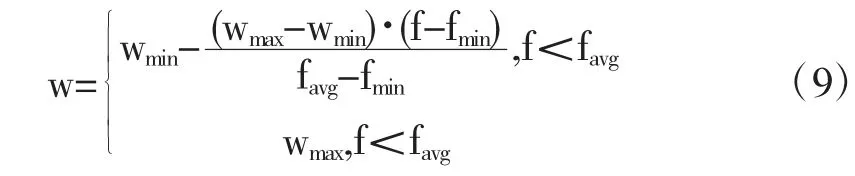
式中：f 为粒子当前目标函数值；favg为全部粒子的平均值；fmin为全部粒子的最小值；

增加自适应权重后，改进后的粒子群算法中粒子的速度和位置变化公式为（10）、（11）：

3.2 引入遗传算法

在遗传算法中，通过交叉、变异两个重要的步骤，可以实现父代和子代之间的信息传递，保证了个体间的优化过程。

在粒子群优化算法中粒子的适应度值越大，其适应度越好，通过将遗传算法（GA）引入粒子群优化算法中，在改进的粒子群优化算法中每次迭代过程均使得粒子适应度值进行由大到小的排列，使适应度值较大的粒子进入下一代，同时将适应度值较大的前一半粒子的速度和位置赋予后一半粒子，两部分粒子作为父代，两两相互交叉，产生数目相同的子代新粒子，并由新粒子代替原有粒子，其子代新粒子的位置及速度公式可以表示为：

式中：p 为0～1 的随机数；parent1(x)、parent2(x)为不同适应度值的父代粒子位置；parent1(v)、parent2(v)为不同适应度值的父代粒子速度；

通过将遗传算法（GA）引入粒子群优化算法中，既增加了粒子的多样性，避免局部最优解的出现，又能实现粒子群优化算法的快速收敛能力。

3.3 改进的GA-PSO 算法优化SVM 模型

根据SVM 基本原理，SVM 模型中的惩罚因子和核函数将影响SVM 模型的应用性能。为了使SVM 模型参数的选择更加全面、合理，提出改进的GA-PSO算法优化SVM 回归模型，将改进的GA-PSO 算法待寻参数设为SVM 的惩罚参数和核函数参数，其基本流程图如图2 所示。

图2 改进的GA-PSO-SVM 回归模型流程图

4 现场实践研究

煤层底板破坏深度的影响因素很多，根据前期收集资料成果，本文选取采深、倾角、采高、工作面长度、底板承压水水压、底板损伤变量作为底板破坏深度预测模型的主控变量，并以枣庄矿业集团下属的柴里煤矿、蒋庄煤矿、新安煤矿、付村煤矿、高庄煤矿、田陈煤矿6 个煤炭生产单位为研究对象，井下采集60 组底板破坏带深度相关数据，如表1 所示。

选取前45 组底板破坏带深度相关数据作为改进的GA-PSO-SVM 煤矿底板破坏深度预测模型训练样本，后15 组作为改进的GA-PSO-SVM 煤矿底板破坏深度预测模型的测试样本。

表1 煤层底板破坏深度影响因素采集数据

运用Matlab 软件编写相关程序，将改进的GA-PSO-SVM 模型的具体参数设置为：粒子群规模设置为40，迭代次数为200 次，SVM 模型的惩罚参数的取值为122.62，核函数参数的取值为11.31，改进的GA-PSO-SVM 模型适应度曲线如图3 所示。

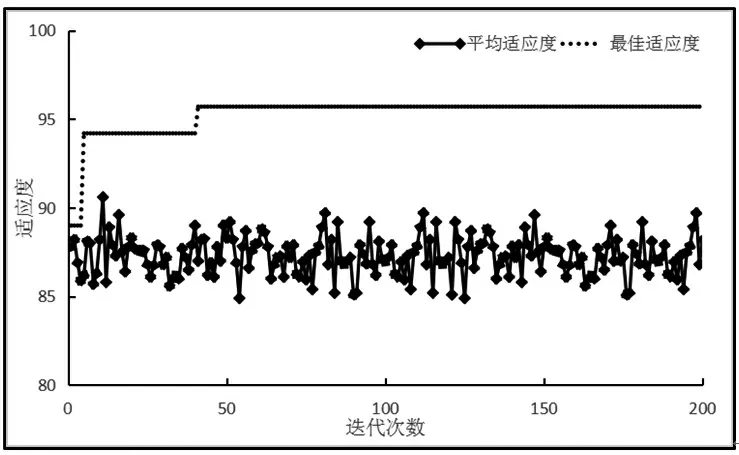
图3 改进的GA-PSO-SVM 模型适应度曲线

将参数带入改进的GA-PSO-SVM 模型中并对训练样本进行训练，将前45 组数据作为训练集对预测模型进行拟合，其结果如图4 所示。

采用训练好的模型对15 个测试样本进行测试，并与FOA-SVM 模型预测结果、BP 模型预测结果与实测结果进行对比分析，各模型预测结果及实际测量结果如表2 所示。

图4 改进的GA-PSO-SVM 模型

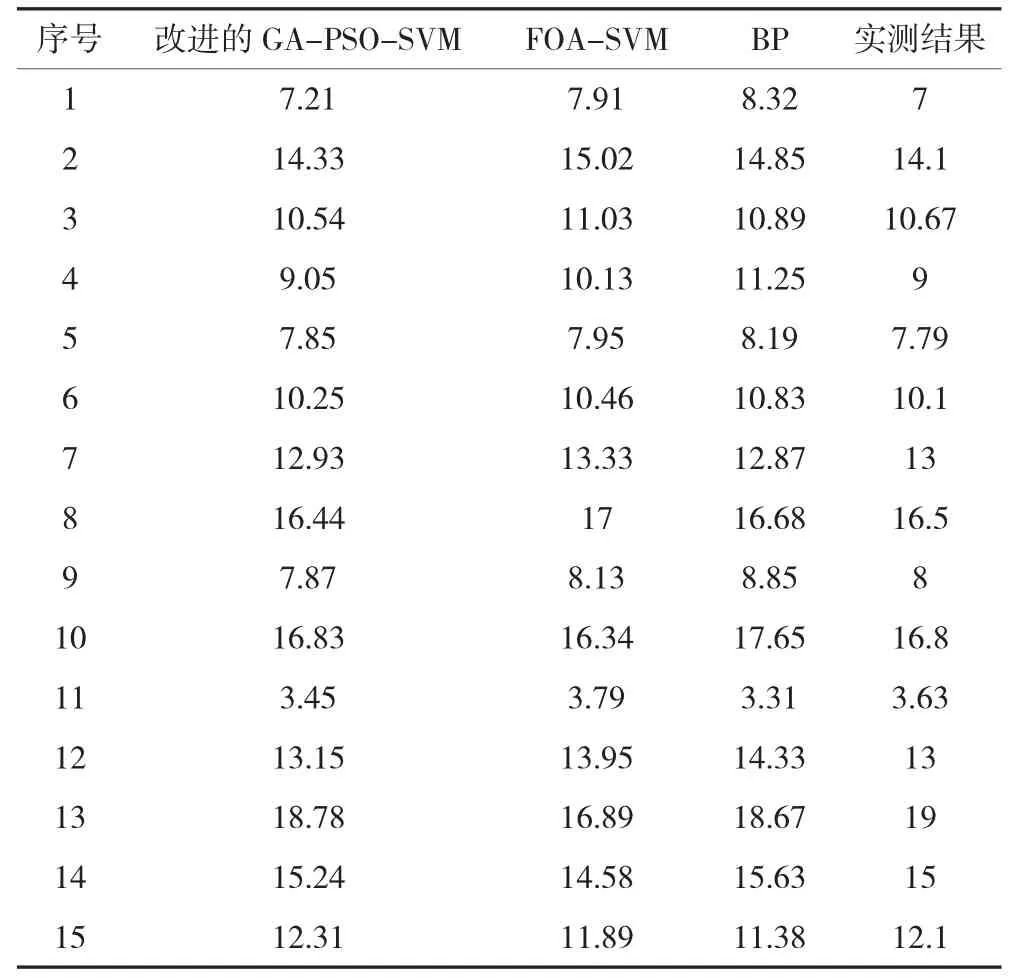
表2 各模型预测结果及实际测量结果

表3 各模型预测结果及实际测量结果之间的误差

由表2 可知，15 组测试样本中应用改进的GA-PSO-SVM 模型预测结果与实测结果的误差范围为0.36%～5.22%，FOA-SVM 模型预测结果与实测结果的误差范围为1.60%～12.49%，BP 模型预测结果与实测结果的误差范围为1.01%～20%。通过各模型预测结果与实测结果的对比知， 改进的GA-PSO-SVM 模型预测结果的误差范围更小，更适合煤矿现场的应用要求。各模型预测结果及实际测量结果之间的误差如表3 所示。

5 结 论

通过提出改进的GA-PSO-SVM 底板破坏深度预测模型，可以得出以下结论：

1）自适应权重值是指粒子前期速度对当前速度的影响程度，其随粒子目标值的改变而改变，当自适应权重值较大时，粒子前期速度对当前速度的影响较大，有利于全局搜索，当自适应权重值较小时，粒子前期速度对当前速度的影响较小，有利于局部搜索，通过调节自适应权重值的大小，可以使粒子群优化算法避开局部极小值，改变粒子的速度状态，增强粒子的全局及局部搜索能力。

2）通过将遗传算法（GA）引入粒子群优化算法中，既增加了粒子的多样性，避免局部最优解的出现，又能实现粒子群优化算法的快速收敛能力。

3）通过测试样本检验结果可以得出：改进的GA-PSO-SVM 底板破坏深度预测模型预测结果与实测结果的误差范围为0.36～5.22%，比FOA-SVM 模型及BP 模型预测结果的误差范围更小，预测精度高，更能真实反应煤层底板的破坏深度。