不可约多项式的一个应用
2021-01-06刘合国廖军
刘合国,廖军
(湖北大学数学与统计学学院, 湖北 武汉 430062)
0 前言
《高等代数》是大学里最基础的课程之一,对于刚刚进入大学的新生而言,它包含了许多新内容、思想和方法,解题的技巧性也很强,这严重影响了一般新生学习这门课程的热情和努力.不可否认的是,《高等代数》里充满了令人眼花缭乱、令人叹为观止的解题方法,学生们或望而却步、自叹不如,或沉迷于此、沾沾自喜.其实,《高等代数》里包含了许多基本概念,深入地理解概念,自觉地运用概念进行思考和解题是学习中非常重要的一个环节. 运用概念进行推理是质朴而有效的学习和训练方法,但它常常被我们在《高等代数》教学时忽视了.本研究拟从一个有名问题及其几种常见解法入手,通过把这个问题进行一般化来检验这些解法的适用范围,由此说明在解题时,理解基本概念是非常必要的,运用基本概念进行推理有助于理解问题的本质.
文献[1]是被广泛采用的经典教材,其第一章处理域上的多项式,涉及一个非常基本的概念:不可约多项式.在某种意义上,不可约多项式是这一章的基石,这个事实可以从下面的重要结论体现出来.
定理1([1,因式分解及唯一性定理])数域F上每一个次数≥1的多项式f(x)都可以唯一地分解成数域F上一些不可约多项式的乘积,所谓唯一性是说,如果有两个分解式
f(x)=p1(x)p2(x)…ps(x)=q1(x)q2(x)…qt(x),
那么必有s=t,并且适当排列因式的次序后有
pi(x)=ciqi(x),i=1,2,…,s,
其中ci(i=1,2,…,s)是一些非零常数.
这是代数学里的一个基本定理.在大学代数类课程里,能与它相匹敌的大概是数论里所谓的算术基本定理.
定理2([2,算术基本定理])任一大于1的整数能表成素数的乘积,即任一大于1的整数
a=p1p2…pn,p1≤p2≤…≤pn,
其中p1,p2,…,pn是素数,并且若
a=q1q2…qm,q1≤q2≤…≤qm,
其中q1,q2,…,qm是素数,则m=n,qi=pi,i=1,2,…,n.
代数学里的一些基本思想可以溯源于这两个定理.我们知道,在通常的运算下,域上所有多项式的集合和所有整数的集合都构成欧几里得整环,由文献[3,第4章定理1],欧几里得整环都是主理想整环,当然他们都是唯一因子分解整环,在这类整环里,每个不可约元都是素元.下面的结果是前面两个定理的一般化.
定理3([3,第4章定理2])整环R是唯一因子分解整环当且仅当R满足:
1) 因子链条件;
2) 每个不可约元都是素元.
在多项式代数里,下面的结果是基础性的,其证明的根本出发点就是上面的定理.
定理4([3,第4章定理5])唯一因子分解整环R上的一元多项式环R[x]仍为唯一因子分解整环.
从上面这些阐述的结果,就存在性而言,我们可以体会到不可约多项式在多项式理论里的重要性.一般域上的多项式f(x),判断f(x)是否是不可约多项式不是一件容易的事,对有理数域来说,下面的判别准则是有用的.
定理5([1,定理13艾森斯坦(Eisenstein)判别法])设
f(x)=anxn+an-1xn-1+…+a0
是一个整系数多项式.如果有一个素数p,使得
1)p⫮an;
2)p|an-1,an-2,…,a0;
3)p2⫮a0.
那么f(x)在有理数域上是不可约的.
不可约多项式和Eisenstein准则能够帮助我们理解一些问题.
1 不可约多项式的一个应用
我们从一个有名的问题即例1开始,即文献[4,例10],其第一种证法取材于文献[4].
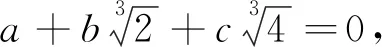
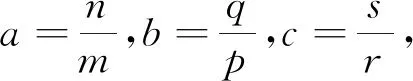
当例1对整数a,b,c成立时,由上式即可导出
prn=mrq=mps=0.
这意味着n=q=s=0,即a=b=c=0.这样在下面的证法一和证法二里,我们不妨假设在a,b,c都是整数的情况下进行推理.
例1的证法一当a,b,c不全为0时,我们假设(a,b,c)=1.当x+y+z=0时,考虑到
a3+2b3+4c3-6abc=0,
由此得到a3是偶数,进而a是偶数,记a=2a1,把它代入上式得到
b3+2c3+4a13-6bca1=0.
于是b3是偶数,b也是偶数,记b=2b1,把它代入上式得到
c3+2a13+4b13-6ca1b1=0,
因此c3是偶数,c也是偶数.与假设(a,b,c)=1.矛盾.所以a,b,c全为0,得证.
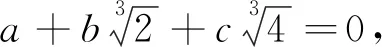
于是,
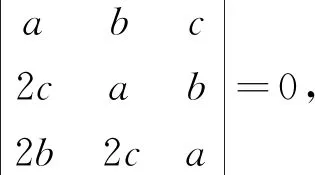
则有
a3+2b3+4c3-6abc=0,
接下来同证法一的推理,得2|a,2|b,2|c.矛盾.
接下来,我们要从多项式的角度来重新证明例1.熟知,对域上的不可约多项式p(x)和任意一个多项式f(x),或者p(x)|f(x),或者(p(x),f(x))=1.由此,我们容易得到一个常识性结论.
例2设p(x)是域F上的一个不可约多项式,f(x)是域F上的一个多项式,若p(x)和f(x)在F的某一个扩域上有一个公共根,则p(x)|f(x).
例2的证明假设p(x)⫮f(x),因为p(x)是域F上的一个不可约多项式,则(p(x),f(x))=1.因此存在多项式u(x),v(x)使得
u(x)p(x)+v(x)f(x)=1,
由于p(x)和f(x)在F的某一个扩域上有一个公共根,设为α.则u(α)p(α)+v(α)f(α)=1,即有0=1矛盾,所以p(x)|f(x).
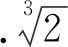
比较例1的3种证明,我们似乎无法判断其优劣,因为他们各有特点.相对于证法一和证法二,证法三还显得不太自然.为了理解得更深一些,我们把例1推广到一般的情形.
例3设a0,a1,a2,…,an-1都是有理数,满足
例3的证明a0=a1=a2=…=an-1=0.
当x+y+z=0时,x3+y3+z3-3xyz=0.这个简洁明快的结论无法推广到一般情况,因为当x1+x2+…+xn=0时,
但这个n阶行列式的展开式非常复杂,我们无法从上面的等式得到所需的有用工具.这样例1的证法一无法适用于例3.
例1的证法二和证法三对例3还是有用的.
例3的证法一我们不妨设a0,a1,a2,…,an-1都是整数,当a0,a1,a2,…,an-1不全为0时,设(a0,a1,a2,…,an-1)=1.根据
可得
于是
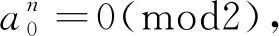
设a0=2a0′,将a0=2a0′代入上述行列式,并将第n行乘以1/2;再将行列式的第n行与第n-1行互换,第n-1行与第n-2行互换,…,第2行与第1行互换,得到
同样的办法可证2|a1.继续这个过程,归纳地可以证明2|ai,i=0,1,…,n-1.矛盾.所以,a0=a1=a2=…=an-1=0.

值得注意的是例3对一般的素数p也成立.即
设p是素数,设a0,a1,a2,…,an-1是有理数,满足
则a0=a1=a2=…=an-1=0.
为了比较例3的证法一和证法二的功效,我们再来看一个下面的例子.

a0+a1ω+a2ω2+…+ap-2ωp-2=0,
证明a0=a1=a2=…=ap-2=0.
我们从线性方程组的角度证明了例1和例3.但无法照搬该方法证明例4.

进一步,我们有下面的结论.
例5设p(x)是数域F上n次不可约多项式.设α是p(x)在复数域C上的一个根,若a0,a1,a2,…,an-1∈F满足
a0+a1α+…+an-1αn-1=0,
则a0=a1=a2=…=an-1=0.
例5的证明设f(x)=a0+a1x+…+an-1xn-1,则α是p(x)和f(x)在复数域C上的一个公共根,又p(x)在数域F上不可约,根据例2,p(x)|f(x),又p(x)的次数大于f(x)的次数,所以f(x)=0,于是a0=a1=a2=…=an-1=0.


这种推理对我们理解多项式的根是有帮助的.
例6设p(x)是数域F上的n次不可约多项式,f(x)∈F[x],E是p(x)的分裂域,p(x)=(x-α1)(x-α2)…(x-αn),若αi是f(x)的一个根,则α1,…,αi-1,αi+1,αn也是f(x)的根.
例6的证明由已知条件和例2得p(x)|f(x),因此α1,…,αi-1,αi+1,αn也是f(x)的根.
设p(x)是数域F上的一个n次不可约多项式,E=F(α1,α2,…,αn)是p(x)的分裂域.则由文献[3,第8章定理5]知多项式p(x)的伽罗瓦群Gp≅Gal(E/F)在p(x)的根集合{α1,α2,…,αn}上的作用是传递的.例6说明,f(x)任一根αi在其极小多项式的伽罗瓦群作用下的像仍然是f(x)的根.
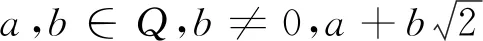



通过上面的论述,我们看到运用基本概念、基本知识解题的重要性,沿着这个思路,我们更能发现问题的本质.1900年大数学家David Hilbert在巴黎国际数学家代表大会上作了《数学问题》的著名演讲,在结尾处掷地有声地说:
数学中每一步真正的进展都与更有力的工具和更简单的方法的发现密切联系着,这些工具和方法同时会有助于理解已有的理论,并把陈旧的、复杂的东西抛在一边,数学科学发展的这种特点是根深蒂固的.
Hilbert的这种真知灼见对每个数学教育工作者都具有警醒作用.
