无动力船舶锚泊防台抗风能力研究
2021-01-06王艳杰交通运输部水运科学研究院
◎ 王艳杰 交通运输部水运科学研究院
无自航能力的驳船、打桩船、海上生活支持船和工程支持船等无动力船舶,避风过程中一旦走锚,无法动车进行抗风、顶浪等操作,可能随风漂移,从而威胁周围船舶、人员以及周边水域的安全,其防台问题至关重要。
船舶的抗风能力大小是防台安全的决定性因素,确定其抗风等级是防台安全的前提条件。
1.稳性衡准与船舶抗风能力
现行的船舶稳性衡准采用“确定性力学分析法”,先把船舶倾覆的物理因素简化为数学模型,通过解析计算,对船舶稳性作出定量评估。上述过程没有直接反映出风级风速的概念,但经过风压换算可以求出风速,即抗风能力,公式如下:
船舶抗风等级:
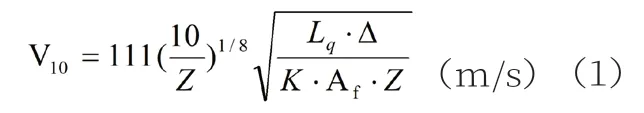
船舶最大抗风等级:
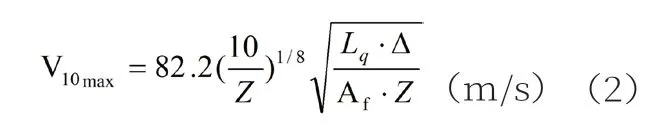
式中:V10—风压作用力臂10m高处的风速;Z—受风面积中心距水面距离,m;Lq—最小倾覆力臂,m;△—排水量,t;K—稳性横准值;Af—受风面积,m2。
2.基于船舶运动规律的抗风能力计算模型
一定载重状态下的无动力船舶,按一定锚泊方式锚泊防台时,船体受到的力主要为风力Fa、水动力Fw、锚链及锚抓力即锚泊力p。在不走锚的前提下,出一定链长时可抵御的船舶可受最大水平外力,称为船舶在该条件下的临界锚泊力。当锚泊力达到临界锚泊力时,船舶所承受的风力最大。此时,船舶受力满足如下条件:
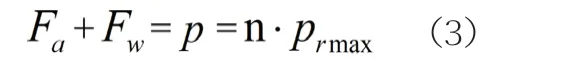
式中:n—船舶实际锚泊状态下产生的锚泊力/单锚泊产生的锚泊力。
单锚泊状态下临界锚泊力prmax(t)可以通过下式计算:
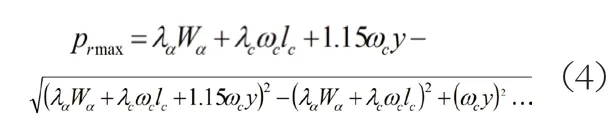
式中:λα—锚抓力系数;λc—锚链抓力系数;Wα—锚重,t;ωc—每米锚链重量,t/m;lc—出链长度,m;y—海底至锚链孔垂直距离,m。
船舶所受风力Fa(N)可通过下式计算:
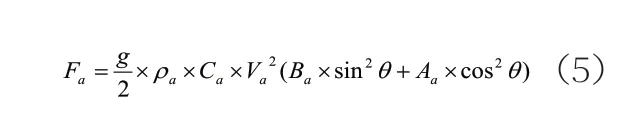
式中:ρa—空气密度;Ca—风动力系数;Va—相对风速,m/s;Aa—水线以上船体正面投影面积,m2;Ba—水线以上船体侧面投影面积,m2;θ—相对风舷角。
船舶所受的水动力Fw(N)可通过下式计算:
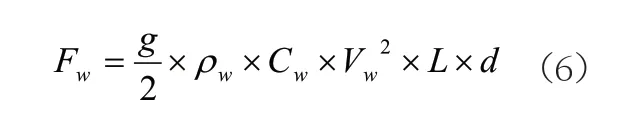
式中:ρw—水密度;CW—水动力系数;VW—船舶与水的相对速度,m/s;L—船舶水线长,m;d—船舶吃水,m。
将式(4~6)代入式(3),单位化为统一,可以反推出船舶临界状态下所受风力Vαmax(m/s)大小,即船舶能抵抗的最大风力:
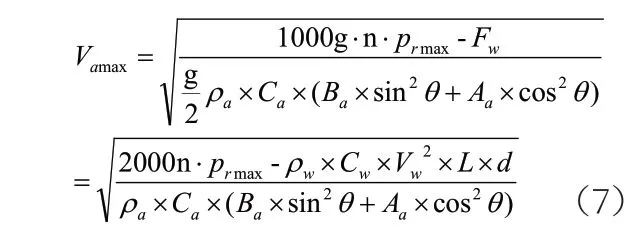
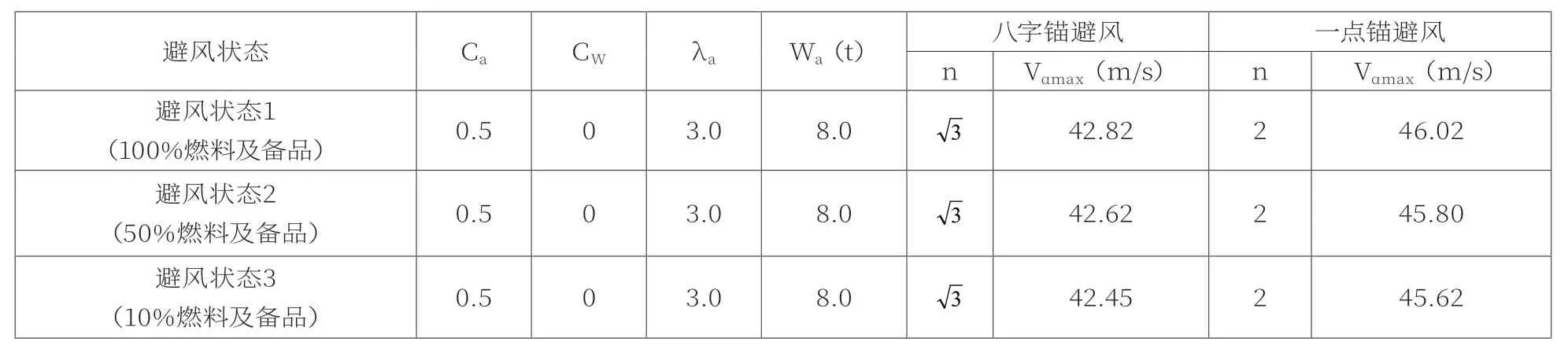
表1 施工船抗风能力(基于船舶运动规律)
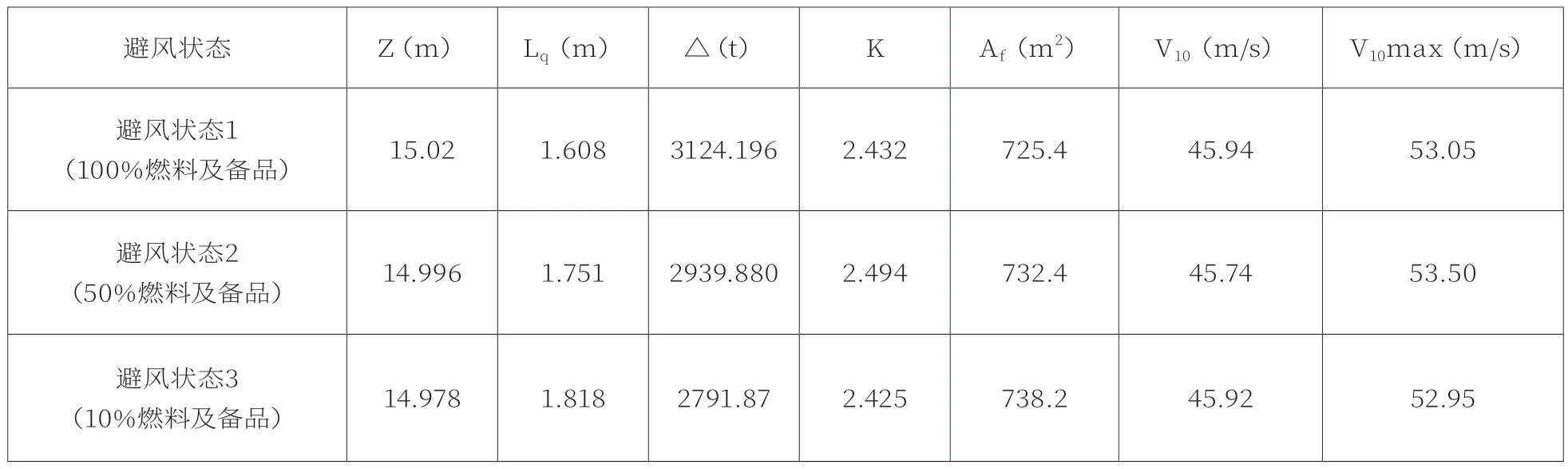
表2 施工船抗风能力(基于稳性衡准)
3.计算实例
珠江口水域是我国水上运输最为活跃的地区之一,也是受台风侵袭较多的地区之一。“砂桩3号”无动力施工船参与港珠澳大桥建设期间,推荐防台水域底质为泥沙和沙泥,防台时抛八字锚或一点锚。根据式(7)计算其不同避风状态下抗风能力大小,如表1所示。
风压换算后可知,八字锚避风时,避风状态1和2情形下抗风等级均为10级阵风,避风状态3情形下为9级阵风;一点锚避风时,在3种避风状态下抗风等级均为10级阵风。
而基于稳性衡准转换得到结果为:“砂桩3号”施工船在3种避风状态下抗风等级均为10级阵风,最大抗风等级均为12级阵风,如表2所示。
基于船舶运动规律得到的抗风能力较基于稳性衡准得到的抗风能力低,且不同的避风状态下抗风能力有一定的差别,在实际运用中偏安全一些。
4.结论
本文提出的基于船舶运动规律的抗风能力计算模型,可以实现对无动力船舶不同避风状态、不同锚泊方式下抗风能力的估算,为驾引人员制定防台方案提供参考。
船舶实际抗风过程中,其外部环境及制约因素十分复杂,各个制约因素之间的关系也是非线性的,抗风能力的量化是一个复杂问题。本文在计算模型建立过程中考虑到的因素可能与船舶实际抗风状态受力情况等有出入。驾引人员在实际操作过程中,可以此为参考,结合船舶相关参数、实际避风经验、相关主管部门的规章制度或指示等,制定合理可行的船舶避风方案。
