基于SADRC的四旋翼姿态解耦控制及稳定性分析
2021-01-06万慧齐晓慧李杰
万慧,齐晓慧,李杰
(陆军工程大学石家庄校区 无人机工程系,石家庄050003)
四旋翼具有可垂直起降、定点悬停、对起飞着陆场地要求低等优势,在民用和军事领域都有广阔的应用前景,近年来逐渐成为航空领域的研究热点之一[1]。目前,对于四旋翼的研究主要集中在四旋翼的位姿控制[2-3]、航迹规划[4]及编队、协同控制[5-7]等方面。
良好的姿态控制系统是四旋翼实现各项功能的前提,而四旋翼本身为欠驱动、强耦合系统,控制难度大,国内外研究人员针对该问题也进行了很多探索和尝试。Bouabdallah团队以小型四旋翼为研究对象,分别设计了基于PID、线性二次型调节器、反步法及滑模控制的姿态控制系统[8-9],并对部分控制方法的控制性能进行了比较;Nicol等[10]将鲁棒自适应控制方法应用于四旋翼姿态控制中;蒋回蓉[11]对基于反馈线性化方法的四旋翼姿态控制进行了研究;张静等[12]对将模糊控制应用于四旋翼姿态控制中进行了尝试。然而,大多数现代控制方法,如反步法、反馈线性化及线性二次型调节器等,虽然具有相对完善的设计方法,但是存在对模型精度要求高、结构复杂、运算量大等问题;滑模控制是飞行控制中应用较多的控制方法,对参数摄动具有较好的鲁棒性,但是该控制结构本身存在抖振问题,当系统不确定性较大时,容易造成控制输入饱和;自适应控制虽然有较好的鲁棒性,但是设计复杂,系统稳定性不易保证;模糊控制虽然在仿真中取得了较好的效果,但是运算量大,使该方法的工程实现存在困难。正因为现代控制方法存在的诸多问题,PID控制仍是现有无人机产品应用最为广泛的控制器,该方法结构简单,参数易于整定,且不依赖精确模型,但是该方法的鲁棒性和抗干扰性并不理想。
自抗扰控制(Active Disturbance Rejection Control,ADRC)技术继承了PID控制的优点,同时吸收借鉴了现代控制理论的部分思想,具有较强的工程实用性,在处理多变量、强耦合系统的控制问题上具有独特优势[13]。目前,已有团队将非线性自抗扰控制(Nonlinear Active Disturbance Rejection Control,NLADRC)和线性自抗扰控制(Linear Active Disturbance Rejection Control,LADRC)应用于四旋翼的控制系统设计中,在所设试验条件下也取得了较为满意的控制结果[14-16]。但是所设试验条件较为简单,而四旋翼实际的工作环境更为复杂,且NLADRC结构复杂,参数整定和稳定性分析困难,而LADRC对初始状态误差敏感,这些问题限制了自抗扰控制技术在四旋翼飞行控制中的进一步应用。
笔者团队在定量对比分析了线性/非线性自抗扰控制各自的特点基础上,提出了综合两者优点的线性/非线性切换自抗扰控制(SADRC)方法。目前,已经完成了针对单入单出(Single-Input Single-Output,SISO)被控对象基于该方法的控制器设计和稳定性分析,并通过算例仿真的方式对该方法的抗干扰能力和跟踪精度进行了初步验证,显示了其在工程领域应用的潜力[17-18]。
本文针对四旋翼姿态控制系统,设计了基于SADRC的姿态解耦控制器,并提出了基于Lyapunov函数的对该解耦控制系统进行稳定性分析的方法。仿真结果表明,所提方法具有良好的抗扰性和对参数摄动的鲁棒性,在工作环境相对复杂的情况下较LADRC和NLADRC更有优势。
1 四旋翼姿态模型
研究用的四旋翼平台如图1所示。该四旋翼无人机本体运动原理同“十”字型飞行方式的四旋翼无人机的运动原理,通过控制螺旋桨的转速实现四旋翼无人机三轴的姿态角的变化。

图1 四旋翼平台Fig.1 Quadrotor aircraft platform

式中:φ、θ、ψ分别为飞行器的俯仰角、滚转角、偏航角;l为四旋翼的臂长;Vi(i=f,b,l,r)分别为“前、后、左、右”4个电机的电压;Kf为电机电压与升力间的系数;Kt为电机电压与转矩之间的系数;qi(i=f,b,l,r)分别为“前、后、左、右”4个旋翼的角速度;Kafi(i=x,y,z)分别表示x,y,z三轴的空气阻力系数;Ji(i=p,r,y)分别为机体绕俯仰轴、滚转轴、偏航轴的转动惯量;Jrz为旋翼转子的转动惯量。
引入虚拟控制量Ui(i=1,2,3),并将各通道间的动态耦合部分视为系统的内部扰动,同时考虑各通道中可能存在的外部扰动wi(i=1,2,3),设η=[φ θ ψ]T,ω=˙η,则式(1)可以进一步整理为

由式(2)可以看出,若设计的控制器可将各通道的“总扰动”进行较好的跟踪和补偿,则各通道可变为串联积分形式,实现多耦合系统的解耦控制。
2 姿态解耦控制方法
2.1 SADRC方法
鉴于线性控制律在实际应用方面的优点,本文采用的SADRC方法实际上是在LADRC框架下,进行线性扩张状态观测器(Linear Extended State Observer,LESO)和非线性扩张状态观测器(Nonlinear Extended State Observer,NLESO)之间的切换[13],系统控制律仍采用线性控制律,其具体结构如下:
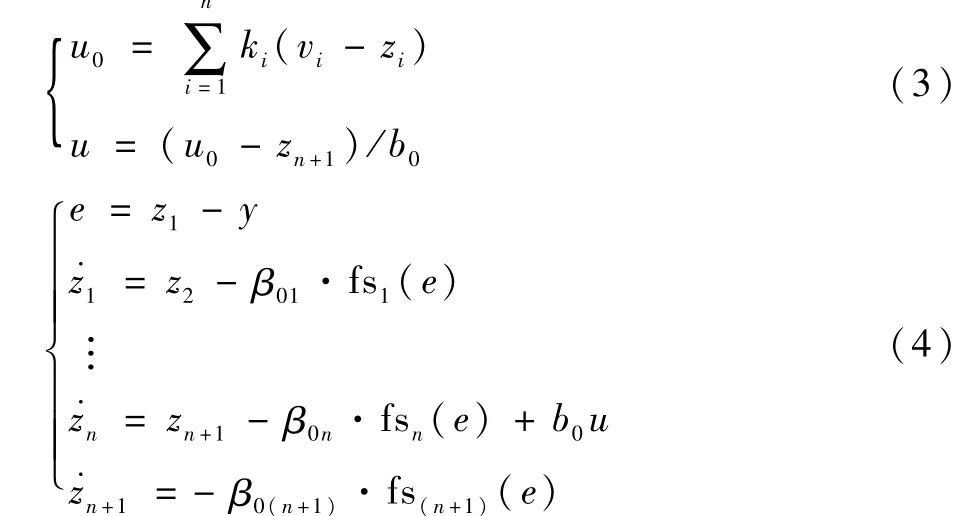
式(3)为线性控制律,用于补偿残差,提高控制系统性能,ki(i=1,2,…,n)为控制器增益。式(4)为切换扩张状态观测器(Switch in nonlinear-linear Extended State Observer,SESO),用于跟踪和补偿系统的“总扰动”。
式(4)中,u和y分别对应系统的控制输入和输出;u0为控制分量;vi(i=1,2,…,n)为系统参考输入各状态的估计值;zi(i=1,2,…,n)为系统各状态的估计值;zn+1为对系统总扰动的估计;b为系统参数,设已知关于b的部分信息b0,并假定b0≈b;β0i(i=1,2,…,n+1)为SESO中NLESO的增益系数,并假设SESO中LESO的增益β0iL(i=1,2,…,n+1)是其NLESO增益β0i(i=1,2,…,n+1)的λi(i=1,2,…,n+1)倍(对NLESO的增益β0i(i=1,2,…,n+1)进行整定,可从“带宽法”角度出发,具体方法在文献[14]中已经给出,这里不再赘述),λi(i=1,2,…,n+1)为常数;则切换函数fsi(e)(i=1,2,…,n+1)具体可表示为


LESO与NLESO的切换步骤具体如下:
步骤1 如果已知系统的初始状态误差,则为避免LADRC控制器的“峰值”现象,在系统的过渡时间内均采用NLESO;如果初始状态误差未知,则跳过步骤1,直接转到步骤2。
步骤2 根据状态误差e大小,控制器在LESO和NLESO间切换。具体方法为:将线性段区间长度δs与误差e的关系作为切换策略依据,预先设定δs(其具体值的确定将在后续参数整定中说明),当e<δs时,采用NLESO估计系统的“总扰动”;反之,则采用LESO估计系统的“总扰动”。这里,δs为LESO与ESO估计性能的临界值,当e<δs时,ESO的估计性能优于LESO,反之,则LESO相比ESO具有更好的估计性能。
上述即为SESO控制器的切换策略,其流程如图2所示。
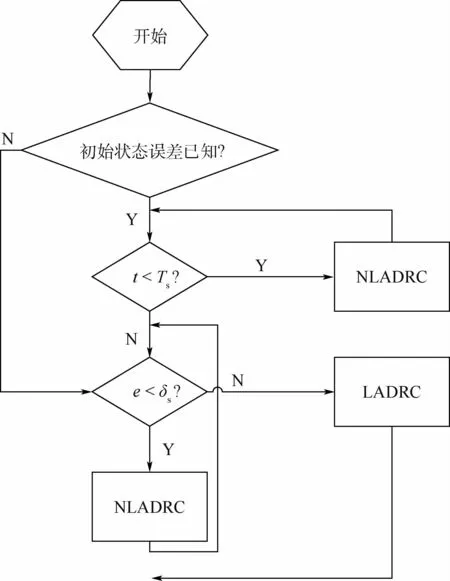
图2 SADRC切换策略Fig.2 SADRC switch scheme
针对δs的确定主要有实验法和理论分析法2种。实验法的主要思想为:将SADRC应用于实际的被控对象或仿真环境下对象的模型,并施加一个较大的扰动,然后给定δs一个初值,重复调整δs直 到 在 该 δs下,SADRC 中 LADRC 和NLADRC性能均达到最优,则此时的δs即为切换策略的临界点。

2.2 基于SADRC的四旋翼姿态解耦控制
结合被控对象实际情况,做出以下假设:
假设1 系统参考输入及其一、二阶导数有界。


式中:AH=A-BK。则控制增益Kη、Kω的选取应使矩阵AH满足Hurwitz条件。在此条件下,总扰动Fdis被SESO估计并补偿,可证明系统式(13)全局渐进稳定。
3 稳定性分析

3.1 观测器误差动力系统稳定性分析



3.2 闭环控制系统稳定性分析


4 仿真实验
本节以3-DOF四旋翼平台为被控对象进行姿态控制数字仿真实验,设计基于SADRC的姿态解耦控制器,并对该方法的抗扰性和鲁棒性与基于LADRC和NLADRC的控制器控制性能进行对比验证。系统参数为:l=0.197 m,Kf=0.118 8 N/V,Kt=0.0036 N·m/V,Kafx=Kafy=0.008 N·m/rad/s,Kafz=0.009 N·m/rad/s,Jp=Jr=0.052 2 kg·m2,Jy=0.11 kg·m2,Jrz=1.91×10-6kg·m2。
将φ、θ、ψ视作系统的一通道、二通道、三通道,则设计的LADRC、NLADRC及SADRC控制器相关参数选择如表1所示。

表1 LADRC、NLADRC、SADRC控制器参数选择Tab1e 1 Parameter pr eferences of LADRC,NLADRC,SADRC
在基于SADRC的四旋翼姿态控制器设计 中,SESO的增益矩阵L可表示为

式 中:βφ0i、βθ0i、βψ0i分 别 为 对 应 通 道 SESO 中NLSEO的增益;λφ0i、λθ0i、λψ0i分别表 示对应通道SESO 中 LESO 的 增 益 为 对 应 通 道 SESO 中NLSEO的增益的倍数。
根据式(7),λφ0i、λθ0i、λψ0i(i=1,2,3)的取值与e的大小有关。为考察e对L的影响,以λφ0i为例,分别做出λφ01、λφ02、λφ03随e大小变化的曲线,如图3所示。

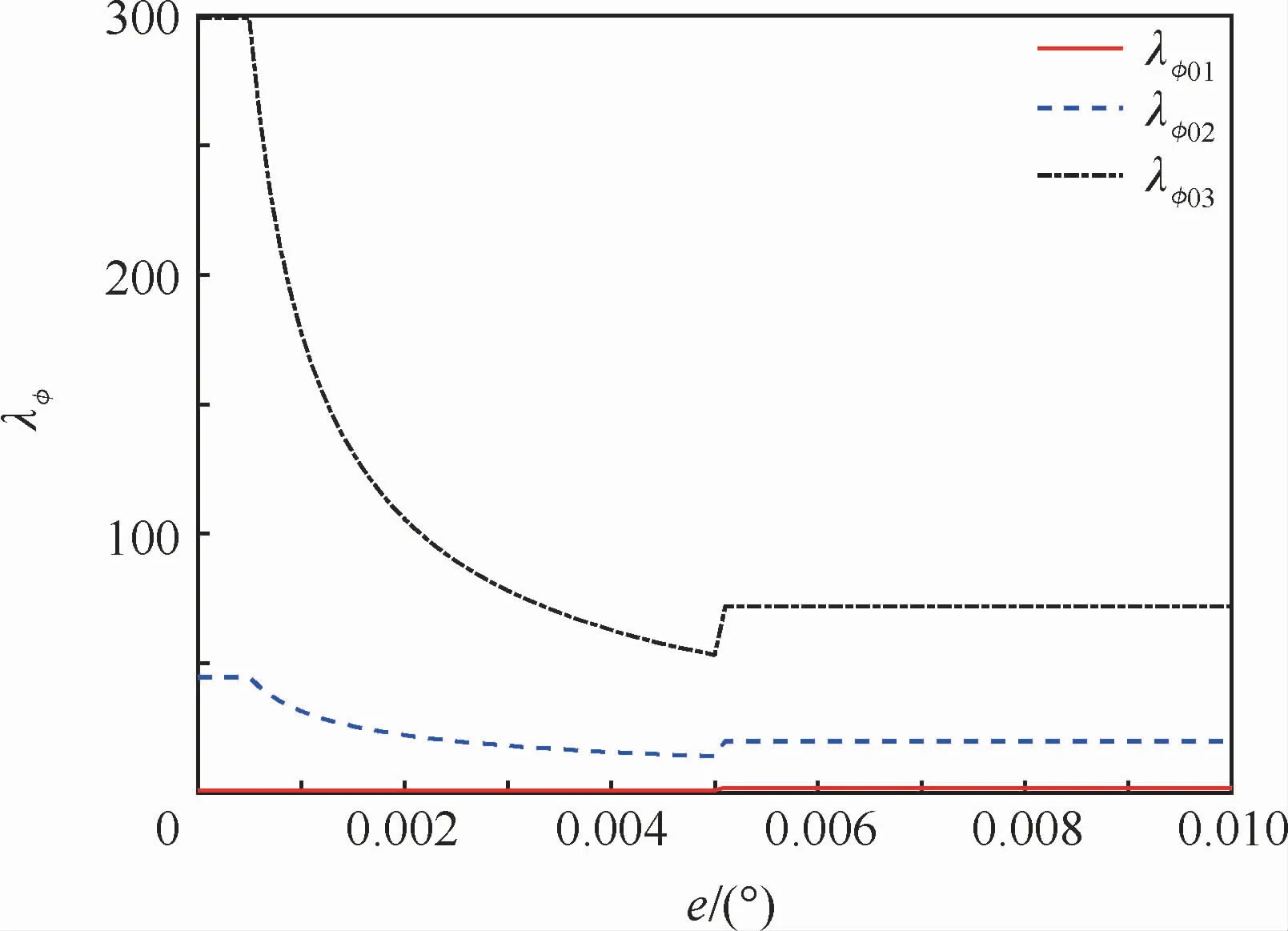
图3 λφ01、λφ02、λφ03随e变化的曲线Fig.3 Curves ofλφ0i(i=1,2,3)changing with e
4.1 抗扰性实验
设置系统3个通道的初始值为φ(0)=0°,θ(0)=0°,ψ(0)=0°,各通道跟踪均为幅值为3°阶跃信号,仿真时间50 s。其中,φ、θ通道分别存在z1φ=0.04°,z1θ=0.4°的初始状态误差,在t=25 s时,分别对各通道输出端施加幅值为0.04°、0.6°、1°,持续时间3 s的干扰信号,对信号的跟踪效果及实际控制量曲线分别如图4、图5所示。
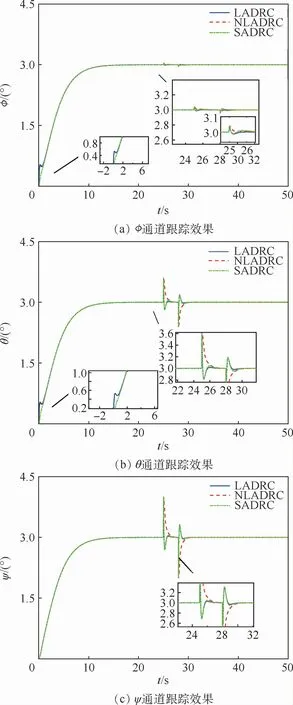
图4 四旋翼φ、θ、ψ通道跟踪和抗扰效果Fig.4 Tracking and anti-disturbance performance for quadrotor ofφ、θ、ψchannel
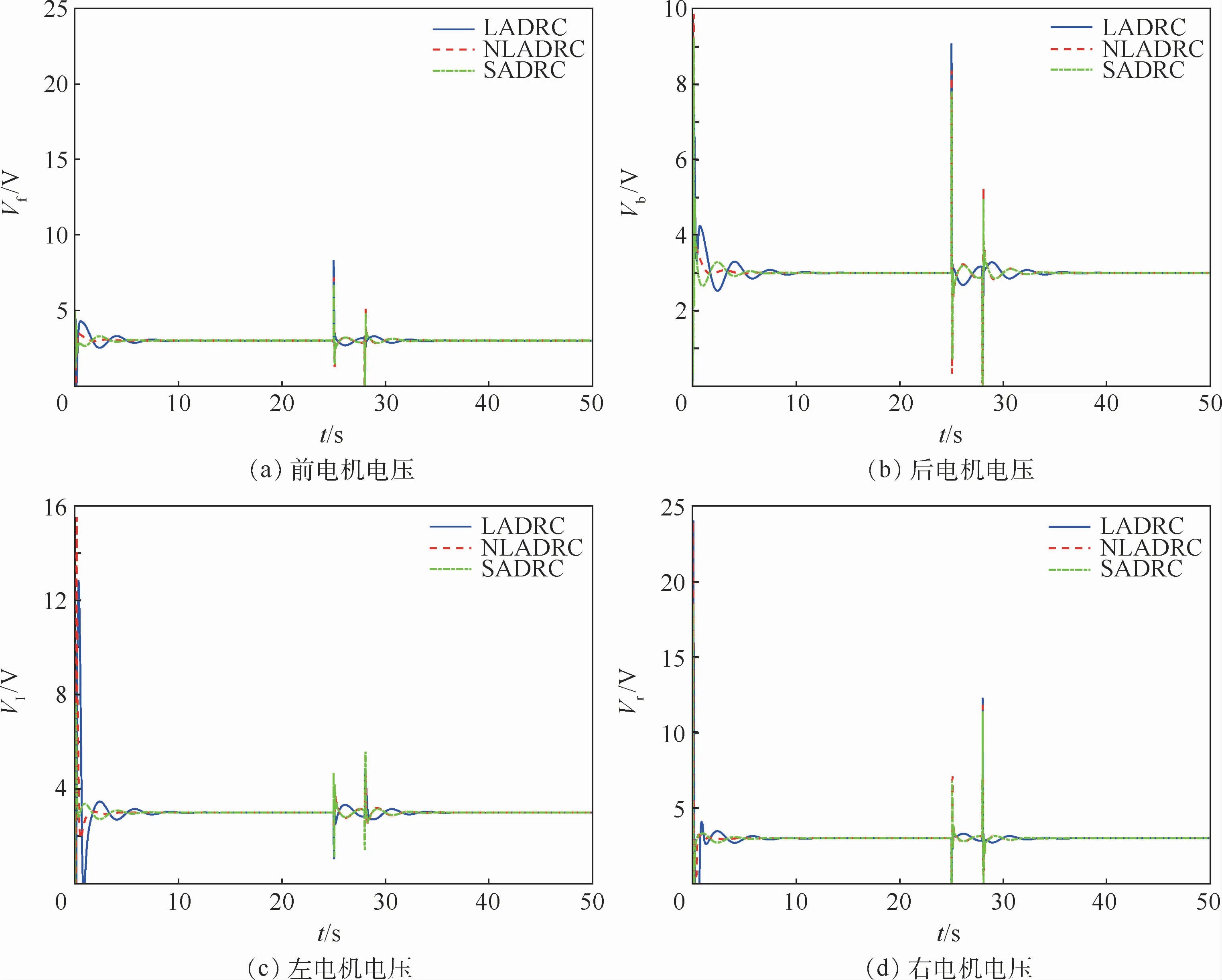
图5 四旋翼实际控制输入曲线Fig.5 Curves of real control input for quadrotor
由图4、图5可以得到以下结论:①3种控制方法均可实现对四旋翼姿态控制系统的解耦控制,且由于虚拟转换矩阵的存在,使得本文所提姿态解耦控制方法在输入输出个数不相等的情况下仍然适用;②LADRC控制器对初始状态误差较为敏感,当被控对象存在初始状态误差时,LADRC可能产生“峰化”现象,使控制性能降低,而NLADRC和SADRC几乎不受初始状态误差的影响;③当被控对象受小扰动干扰时(本文对扰动大小的判断主要根据扰动对系统输出的影响进行定义,本文中定义当系统受扰后瞬时最大输出超过期望输出的5%及以上时,所受扰动为大干扰,小于5%则为小干扰),LADRC、NLADRC和SADRC的控制性能相差不大,这是因为本文中3种控制器的观测器参数选择均可对系统所受小扰动进行快速地估计和补偿,LADRC和SADRC的控制性能要优于NLADRC,这是因为在大误差条件下,LESO 的增益大于NLESO,LESO可更加快速地对所受扰动进行估计和补偿。综合而言,相对LADRC和NLADRC,SADRC控制器可适应更为复杂的扰动情况,具有良好的抗扰性能。
4.2 鲁棒性实验
设置三通道初始值φ(0)=0°,θ(0)=0°,ψ(0)=0°,且均不存在初始状态误差,在t=0 s,各通道跟踪均为幅值为3°的阶跃信号,仿真时间50 s。每次仿真前,对模型参数随机施加±10%的变化,采用误差绝对值积分(Integrated Absolute Error,IAE)准则和能量消耗对控制系统鲁棒性进行评价,其中系统的IAE值为各通道误差绝对值积分之和,系统的能量消耗则用各通道控制输入绝对值积分(Integrated Absolute Control Input,IACI)之和进行表示,每次仿真记录各控制器的IAE值、IACI值、超调量σ、受扰动后的恢复时间tr。在以下3种仿真条件下,各重复仿真200次,得到每次各控制器IAE值与σ的关系、IACI值与tr的关系,如图6所示,仿真条件如下:
仿真条件1 各通道均不存在干扰信号。
仿真条件2 在t=25 s时,分别对各通道施加幅值为0.001°的干扰信号,持续至仿真结束。
仿真条件3 在t=25 s时,分别对各通道施加幅值为1°的干扰信号,持续至仿真结束。
由图6可以得到如下结论:①从点的离散程度看,在存在参数摄动的情况下,3种控制方法均具有良好的鲁棒性和抗扰性;②在小扰动条件下,3种控制方法的IAE无明显差别,进一步证明了本文中3种控制器的观测器参数选择均可对系统所受小扰动进行快速地估计和补偿,但是非线性机制使得NLADRC和SADRC在小扰动条件下恢复速度及能量消耗上较LADRC更低;③在大扰动条件下,LADRC和SADRC在IAE及受扰后的恢复速度方面更有优势,这是因为LESO的观测器增益较大,可对大扰动实现快速地估计和补偿,但是NLADRC在能量消耗方面有明显优势。
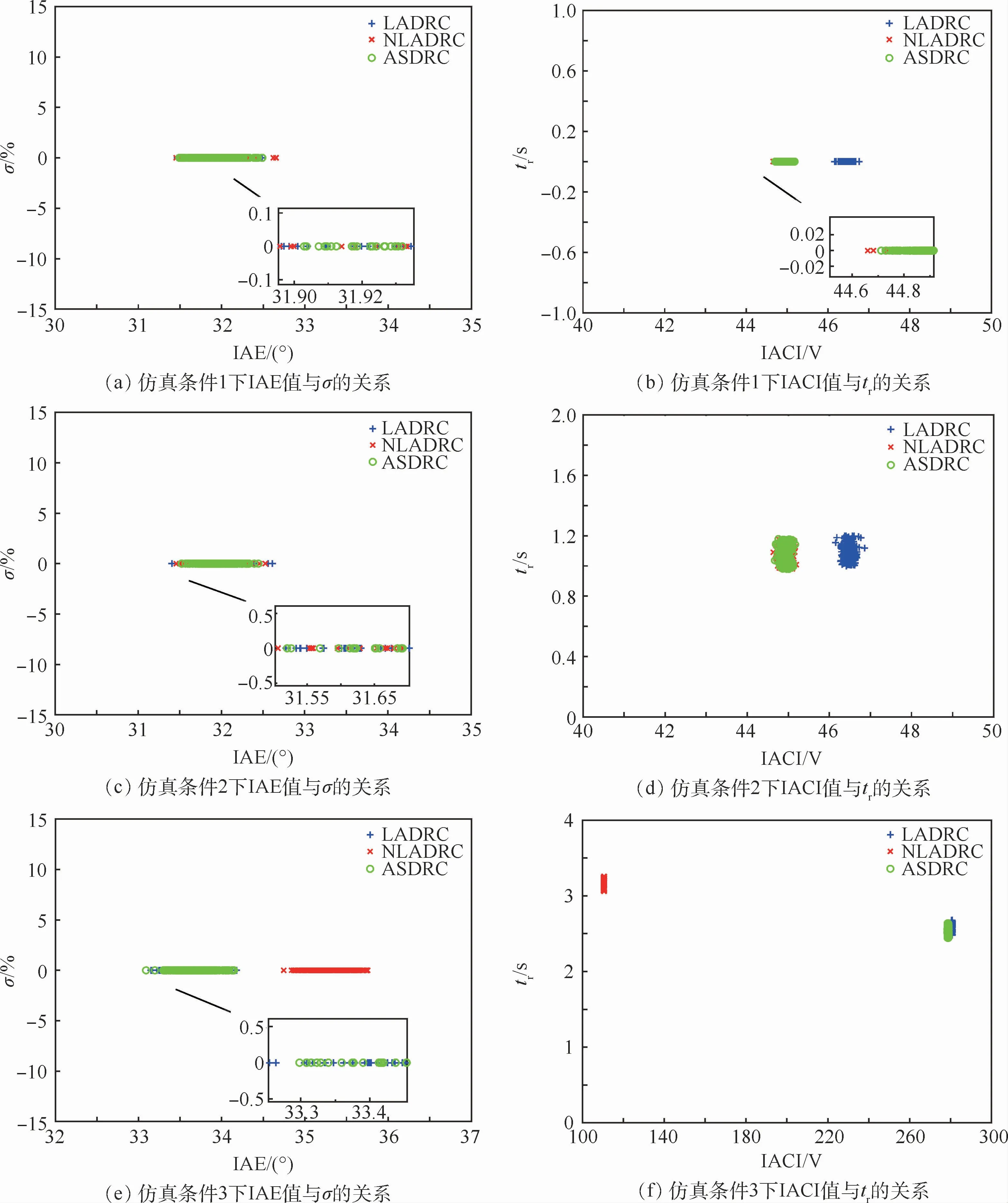
图6 参数摄动情况下3种控制方法的鲁棒性性能Fig.6 Robustness performance for the three controlled quadrotor system
5 结 论
1)本文对四旋翼姿态控制进行研究,设计了基于线性/非线性切换自抗扰控制的四旋翼姿态解耦控制器。
2)将切换自抗扰控制方法应用于多入多出被控对象,拓展了该方法的适用范围,并针对基于SADRC的多入多出控制系统提出了一种基于Lyapunov函数,借助计算机解算,便于工程应用的稳定性分析方法,同时为控制器参数选择提供参考。
3)线性自抗扰控制器、非线性自抗扰控制器及切换自抗扰控制器均具有良好的抗扰性和鲁棒性,其中切换自抗扰控制器在所受扰动较为复杂,如扰动大小不确定或者扰动幅值存在较大波动的情况下更有优势。具体采用何种控制器,可结合具体被控对象、工作环境及控制需求决定。
本文所提方法虽然结构简单,便于应用,但是理论上不够严谨,后续将进一步对稳定性分析方法进行研究,对被控系统的闭环稳定性给出更为严格的证明。
