多表冗余惯导数据融合算法及在自对准中的应用

郭建刚，陈鹏，郑伟

（1.国防科技大学 空天科学学院，长沙410073； 2.北京航天时代激光导航技术有限责任公司，北京100094；3.上海航天技术研究院北京研发中心，北京100081）

激光陀螺捷联惯导系统（Laser Strapdown Inertial Navigation System，LSINS）具有动态范围广、耐冲击振动、可靠性高等优点，远征一号、嫦娥探测器等空间飞行器及多数现役火箭均采用LSINS提供姿态、位置等导航信息。多表冗余惯导系统通过仪表冗余设计，显著提高系统的可靠性，国外如波音777飞机的FT／ADIRS（Fault-Tolerant／Air Data Inertial Reference System）容错大气数据参考系统和“德尔它”系列火箭的RIFCA（Redundant Inertial Flight Control Assembly）冗余激光捷联惯导系统［1］等都采用了多表冗余设计。国内对多表冗余惯导系统进行了多年的研究与探索，已有多型采用三正交加斜置冗余配置的惯导系统得到工程应用，其中斜置冗余仪表仅用于故障检测。

空间飞行器等起飞前需要通过初始对准获得姿态初值，目前普遍使用光学瞄准方案。与光学瞄准相比，惯导自对准需要的设备和人力更少，操作流程大大简化，更符合当前低成本、快速发射的发展趋势［2］。国内外的专家学者对晃动基座上的自对准技术进行了大量研究，提出了许多更优的自对准方案和自对准算法，显著提高了对准精度［3-6］。

对于多表冗余惯导系统而言，冗余仪表用于故障检测和隔离，同时还可通过数据融合技术提高惯导系统的测量和导航精度［7-10］。通过多传感器数据融合技术，充分利用所有的冗余测量数据，可以得到姿态和速度信息的最优估计值。数据融合技术可以有效抑制测量数据中的随机误差，为提高惯导系统自对准精度提供了另外一条有效途径。

本文基于某型多表冗余惯导系统，对数据融合技术在多表冗余惯导系统自对准中的应用及数据融合算法进行了研究。

1 数据融合算法

1.1 惯导仪表构型

该型惯导系统采用三正交两斜置的十表（5只激光陀螺，5只石英加速度计）冗余设计，其中斜置仪表只用于判故。惯导系统中，陀螺和加速度计的安装定向方式如图1所示，仪表测量矩阵如式（1）所示。

图1中，X1Y1Z1为载体坐标系，OX1为纵轴，OY1为法向轴，OZ1为横向轴；XsYsZs为惯导坐标系，OS轴正向与OXs、OYs、OZs轴正向的夹角分别为125.9°、46.6°、115.4°，OT轴正向 与OXs、OYs、OZs轴 正 向 的 夹 角 分 别 为46.5°、56.5°、118.0°；向量Gi和Ai分别为第i只陀螺和第i只加速度计的测量轴向，i＝x，y，z，s，t。

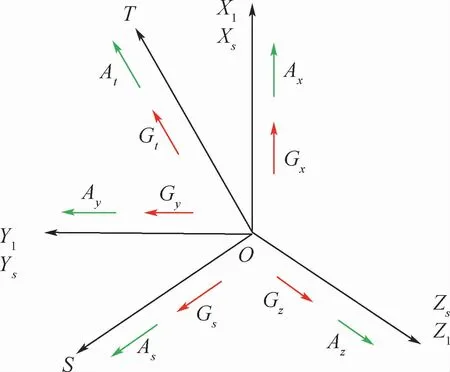
图1 惯性仪表安装定向示意图Fig.1 Schematic diagram of inertial instrument installation orientation

1.2 基于最小二乘的数据融合算法

最小二乘估计（Least Square Estimation，LSE）的特点是算法简单，不必知道与被估计量及量测量有关的任何统计信息［11］。NASA的SIRU项目使用加权最小二乘（Weighted Least Squares Estimation，WLSE）算法进行冗余仪表的数据融合［12］。

对于测量系统：

式中：X为n维状态矢量；Z为m维量测量；H 为m×n维量测矩阵，m＞n；V为m维测量噪声，其均值为零，方差阵为R。

X的最小二乘估计为

式中：Ng和Na分别为陀螺和加速度计的测量输出，m维向量，m为陀螺或加速度计的数量；Kg和Ka分别为陀螺和加速度计的当量矩阵，m阶对角阵；Dg和Da分别为陀螺和加速度计零偏，m维向量；d t为系统采样时间间隔；Hg和Ha分别为陀螺和加速度计的一次项系数矩阵，也即测量矩阵，m×3维，当不考虑零部件加工和安装误差时，Hg＝Ha；Δθ和ΔV分别为载体在d t时间内的角增量和速度增量，3维向量；Vg和Va分别为陀螺和加速度计的测量噪声，m维向量，均值为零，其方差阵分别为Rg和Ra。

1.3 算法精度分析

不考虑零部件加工和安装误差，陀螺和加速度计系统的测量矩阵均如式（1）所示，假设5只仪表（陀螺或者加速度计）的测量精度相同，输出标准差均为1σ。

1）只使用正交仪表数据

3个轴向的输出标准差为

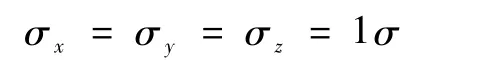
2 Monte Car1o仿真

编写了MATLAB仿真计算程序，对静基座上的自对准进行仿真，仿真中惯导坐标系与地理坐标系（东北天坐标系）重合。工程上通常挑选精度较好的仪表安装在正交轴向，斜置方向仪表精度略差，如正交仪表精度为0.01（°）／h左右，而斜置仪表精度范围为0.015～0.02（°）／h。因此，仿真中假设斜置仪表噪声标准差比正交仪表高50%，并使用马尔可夫估计进行数据融合。为对算法在不同仪表精度下的融合效果进行对比，共进行了4组不同精度的仿真，每组进行500次Monte Carlo打靶。分别通过：①只使用3只正交仪表数据直接解算；②通过式（7）进行5只仪表的数据融合，2种方法得到的自对准结果进行对比，偏航角的统计结果如表1所示。

结果表明，相较于只使用正交仪表数据，通过数据融合同时使用5只仪表数据，可以有效提高惯导偏航角自对准精度，其中误差均值降低了11%，对准结果统计标准差降低了14%。这表明对于如式（1）所示的三正交两斜置惯导系统，即便斜置仪表精度显著低于正交仪表，通过数据融合，仍然能够显著提高惯导的自对准精度，使斜置冗余仪表数据得到充分利用。

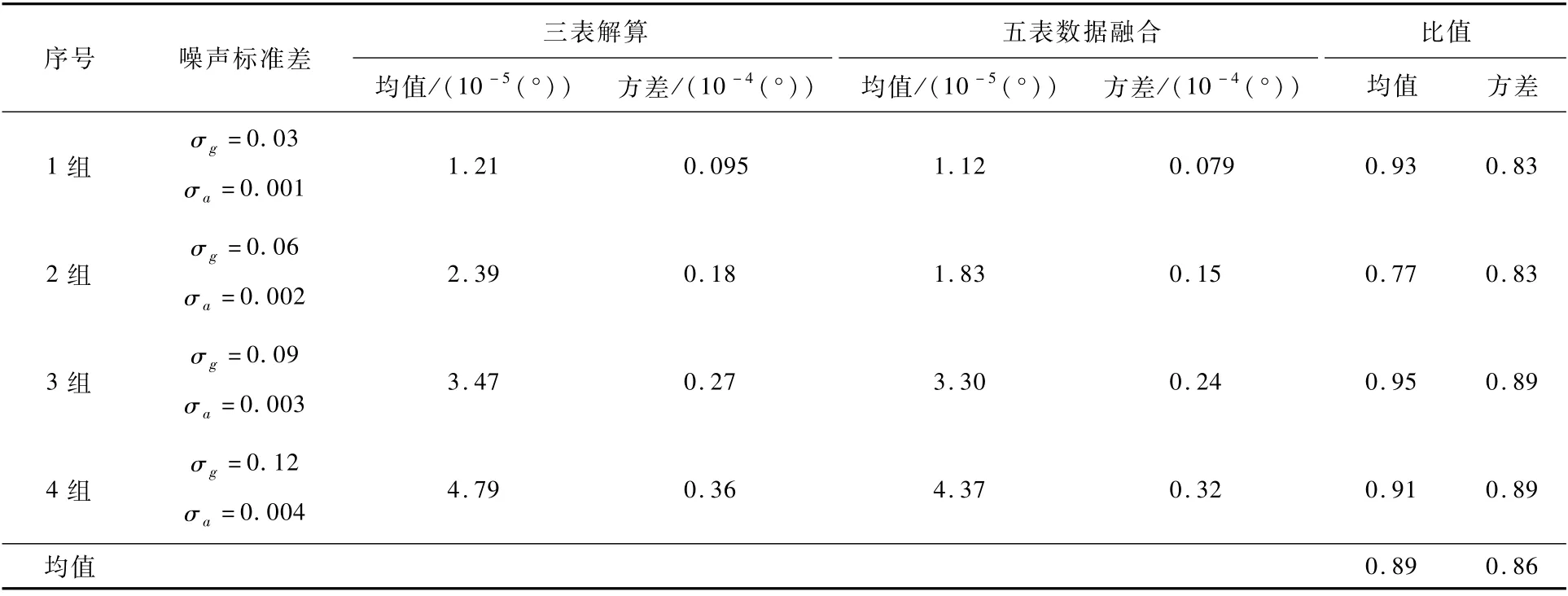
表1 偏航角误差的Monte Car1o仿真结果对比Tab1e 1 Comparison of Monte Car1o simu1ation resu1ts of vaw ang1e error

3 自对准试验和算法改进

3.1 静态自对准试验

为验证本文中数据融合算法的有效性，利用该型惯导系统在大理石平板上进行了静态自对准试验。5只激光陀螺的零偏稳定性在0.01（°）／h左右。试验时，将惯组固联在六面体工装上，惯导按照地理坐标系（东北天坐标系）放置，工装靠紧大理石平板靠块，如图2所示，对准时间5 min，共进行12组试验。

图2 激光陀螺捷联惯导自对准试验Fig.2 Self-alignment experiment of LSINS

考虑试验现场条件无法获取惯导系统真实的航向基准，为了评估算法的有效性，采用在同一方位下进行多次对准，以多次对准结果的标准差的方法间接进行评估［14］。每组试验数据分别通过3只正交仪表直接解算和5只仪表数据融合2种方法进行处理，得到Δθ和ΔV，然后进行自对准。

试验中使用如式（7）所示的马尔可夫估计进行数据融合，对2种方法的自对准结果进行对比，如表2所示。只使用正交仪表直接解算时，偏航角的统计标准差为2.8′（1σ），同时使用5只仪表数据进行数据融合时，偏航角的统计标准差为2.4′（1σ），精度提高了14%。

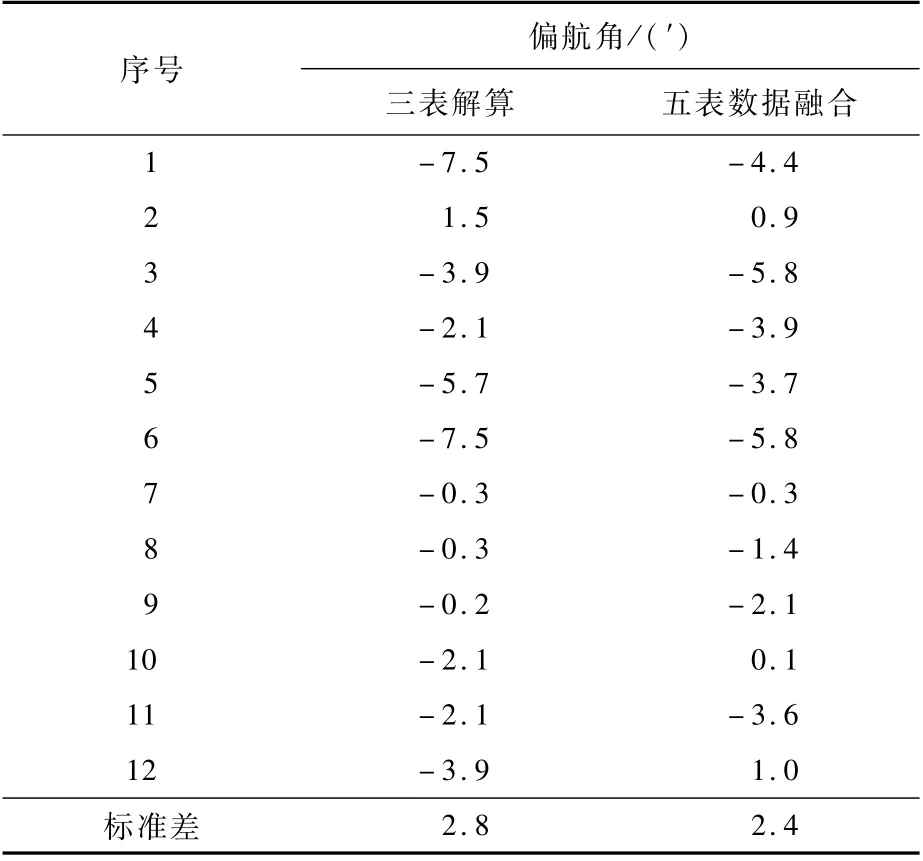
表2 偏航角自对准结果对比Tab1e 2 Se1f-a1ignment r esu1t comparison of vaw ang1es

3.2 加权矩阵的优化

该型惯导系统各仪表原始输出均为脉冲形式，间隔20 ms，输出脉冲数对应惯导在惯性坐标系下的角增量和速度增量。静态自对准试验时，由于地球自转角速度和重力加速度较小，导致仪表输出的量化误差明显。试验中仪表的一段输出数据如表3所示，其中Ai和Gi（i＝x，y，z，s，t）分别为第i只陀螺和加速度计的脉冲输出。同时，仪表输出噪声非白噪声形式，尤其是激光陀螺。因此，对仪表输出直接取方差不能反映仪表精度状况，影响了基于数据方差的马尔可夫估计的数据融合算法的效果。

惯性仪表的零偏稳定性是衡量仪表精度、影响导航误差的重要参数，同时仪表零偏稳定性也比较容易准确获得。因此，选择各仪表的零偏稳定性作为加权系数，构造如式（8）所示的加权矩阵，其中Ωi（i＝x，y，z，s，t）为第i只陀螺和加速度计的零偏稳定性。

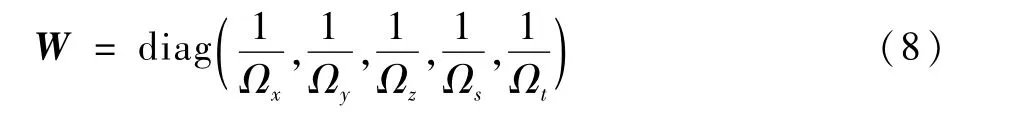
使用如式（8）所示的加权矩阵和加权最小二乘估计的数据融合算法，对试验数据重新进行处理，结果如表4所示，偏航角的统计标准差为2.1′（1σ）。相较于马尔可夫估计，通过加权最小二乘算法和式（8）所示的加权矩阵进行数据融合，自对准精度进一步提高。

多表冗余惯导系统在实际工程应用中需要先经故障诊断技术对故障仪表进行诊断隔离，再使用正常仪表完成系统重构。惯导系统自对准过程中，火箭受发射场阵风等干扰因素的影响，箭体产生顺风向和横风向晃动［15］，但晃动频率较低、量级较小；同时可以通过地测对载荷和火箭惯导系统的输出进行地面判读。因此，初始对准过程中不用担心惯导系统冗余仪表的判故问题，上述数据融合算法有一定的工程实用价值。

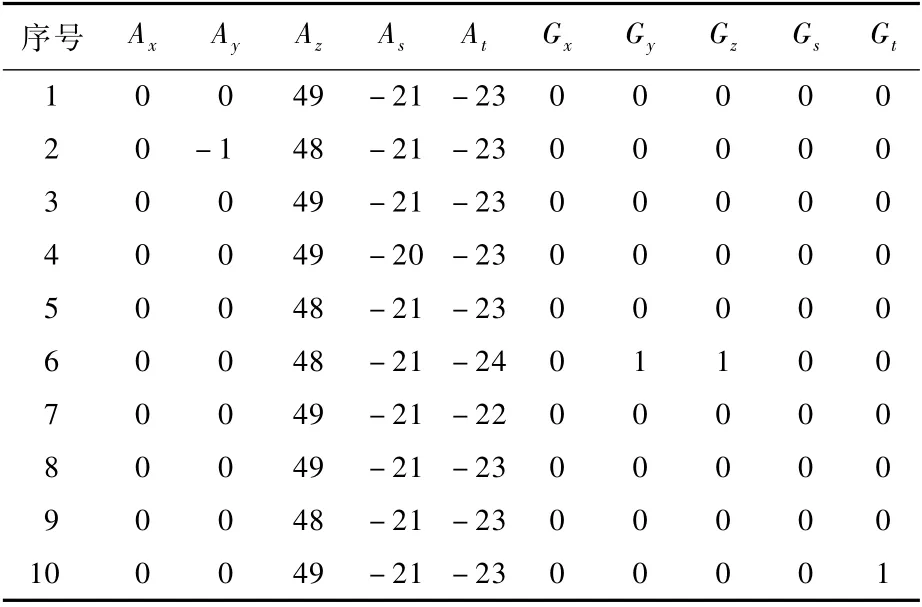
表3 仪表20 ms脉冲增量输出Tab1e 3 Incrementa1 pu1se output of sensors with 20 ms interva1

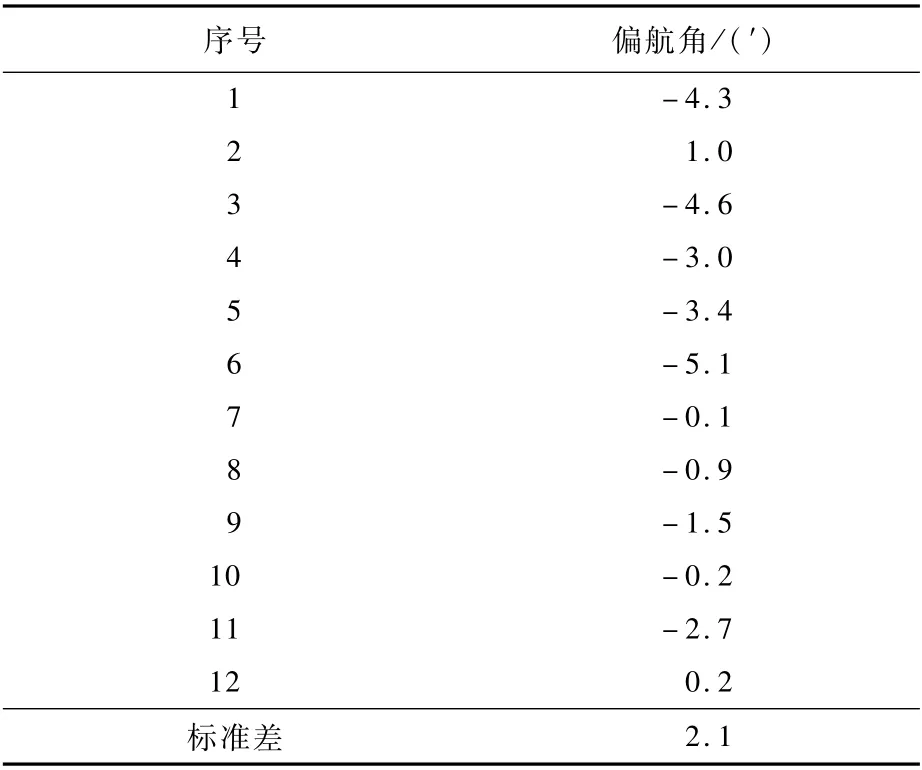
表4 五表数据融合的偏航角自对准结果Tab1e 4 Se1f-a1ignment resu1ts of vaw ang1es bv data fusion of five instruments

4 结 论

基于某型三正交两斜置冗余的十表惯导系统，针对其自对准过程中的数据融合问题：

1）通过分析和仿真，证明数据融合技术可以有效提高多表冗余惯导系统的自对准精度。

2）开展惯导静态自对准试验，结果表明，相较于只使用正交仪表的数据，数据融合可以使斜置冗余仪表的数据得到充分利用，系统自对准精度提高了16%。

3）在静态自对准试验的基础上，构造了基于仪表零偏稳定性的加权矩阵，改进后的算法比马尔可夫估计的略有提高。