弧形金属基超硬磨料砂轮在位精密修形的研究*
2021-01-05关佳亮尚海洋张孝辉郭奎崇徐真真王建杰
关佳亮 尚海洋 张孝辉 郭奎崇 徐真真 王建杰
(①北京工业大学先进制造技术北京市重点实验室,北京 100124;②河南科技大学高端轴承摩擦学技术与应用国家地方联合工程实验室,河南 洛阳 471023;③北京卫星制造厂有限公司,北京 100000)
金属基超硬磨料砂轮具有硬度高、形状保持性好、使用寿命长、磨削精度和效率高的优点,有效解决了难加工材料的磨削精度和效率低的难题[1-3]。但由于其本身具备的特点,也给其精密修形带来很大问题[4]。华南理工大学党希敏通过计算,计算出圆弧插补运动轨迹,使用金刚石砂轮与GC磨石对磨,当定位精度不超过0.1 mm时,修整后的最大形状偏差在5 μm/10 mm以内[5];厦门理工学院柯晓龙利用杯型砂轮修整法对弧形金属基砂轮进行精密修形,利用修形误差进行补偿加工,得到砂轮半径拟合残差PV值为8.5 μm的轮廓表面[6];山东大学朱家豪建立弧形金属基超硬磨料砂轮与金刚石滚轮的几何关系模型,提出螺旋插补修整法,并对其进行误差补偿,得到圆弧轮廓偏差PV值为5 μm的轮廓表面[7]。但是上述方法不仅对滚轮轴的硬度和刚度提出较高的要求,也对砂轮轴提出较高的要求[8],并且这些方法是通过滚轮自身的消耗才能获得被磨砂轮的轮廓,造成成本的浪费,后期需要进行大量计算对其进行误差补偿才能保证较高的修形精度。金属基超硬磨料砂轮由于自身的优点决定了其不可代替性,因此很多学者提出新的修整方法,比如在线电解法和电火花修整法等,但在线电解法更适应于砂轮的修锐工作[9-10],所以近年来广泛采用电火花加工法对金属基超硬磨料砂轮进行高精度、高效率修形的工艺技术,解决了平行金属基超硬磨料砂轮的高效精密修形的问题,但采用电火花加工的方法对弧形金属基超硬磨料砂轮进行精密成型修形技术的探索比较少,本文针对这一问题,以圆弧金属基超硬磨料砂轮在位精密成形修形为例,开展了金属基超硬磨料砂轮在位精密成形修形技术的实验研究。
1 电火花在位修形机理
电火花在位修形是指将砂轮作为电火花加工中的阴极保持位置不变,将位置可调的电极作为阳极,与砂轮靠近,通过在砂轮和电极之间喷洒介质构成火花通路。利用介质在高压作用下,瞬间被击穿所产生的大量热,使磨粒碳化,砂轮表面结合剂高温熔化甚至气化,达到修形效果[11-12]。电火花修形砂轮原理图如图1所示。
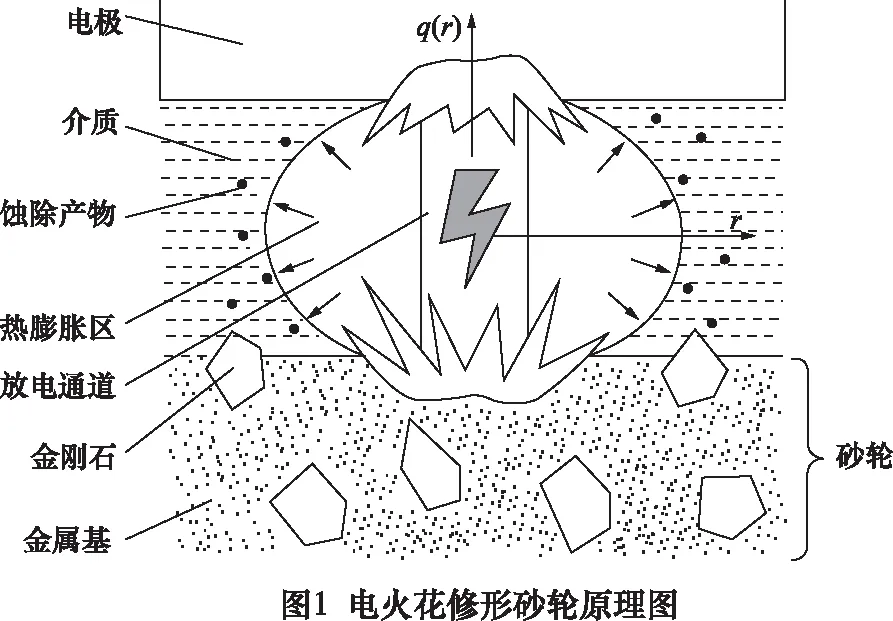
2 实验
2.1 实验方案
以紫铜作为加工电极,采用在位精密数控车削的方法获得能够达到加工要求的弧形加工电极,加工过程如图2所示。为了减小装配误差,故将W40弧形金属基超硬磨料砂轮通过一次装卡固定于床身,加工好的电极通过滚珠丝杠实现与砂轮之间微米级的调整,利用电火花技术对其进行精密成形修形,实验平台如表1所示。
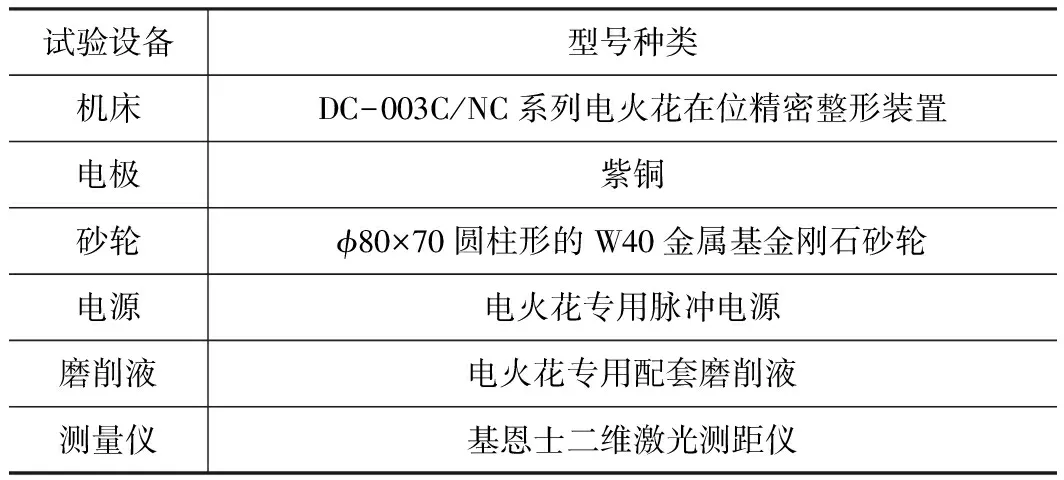
表1 实验平台构建

2.2 实验设计
二次通用回归旋转组合优化设计法能够分析各因素对实验指标的影响大小和规律,适用于影响因素较多的复杂场合[13],影响金属基超硬磨料砂轮轮廓偏差PV值的因素有很多,主要分为电参数和非电参数[14],故本实验采用“二次通用回归旋转组合优化设计法”对砂轮轮廓偏差PV值影响的主要因素进行分析和优化。为了减少实验量,本实验自变量取m,放电间隙、放电电流、占空比、砂轮转速分别用Z1、Z2、Z3、Z4表示。根据本实验的前期模拟实验结果和实际加工条件确定以上四因素的上、下水平如表2所示。根据二次通用旋转组合回归设计原理各实验因素水平编码如表3所示,即将实际实验中有单位的自然变量因素Zm(m=1,2,3,4)通过编码公式转换成无单位的规范变量编码因素Xm(m=1,2,3,4)。在每一组工艺参数下进行4次在线电火花修形工艺实验。为了反映砂轮的实际圆弧轮廓形状,在测量时砂轮保持均匀旋转,用基恩士二维激光测距仪测量完成后得到一条圆弧曲线,可以认为该曲线就是修形后砂轮的实际圆弧轮廓,用MATLAB导入数据作图将该曲线与理想圆弧曲线作对比,计算在半径方向上与理想曲线的偏差,即可得到修形后砂轮圆弧廓形偏差曲线[7],从而得到砂轮轮廓偏差PV值。取4次实验的平均值,记录结果如表4所示。

表2 各实验因素取值范围

表3 各实验因素水平编码表
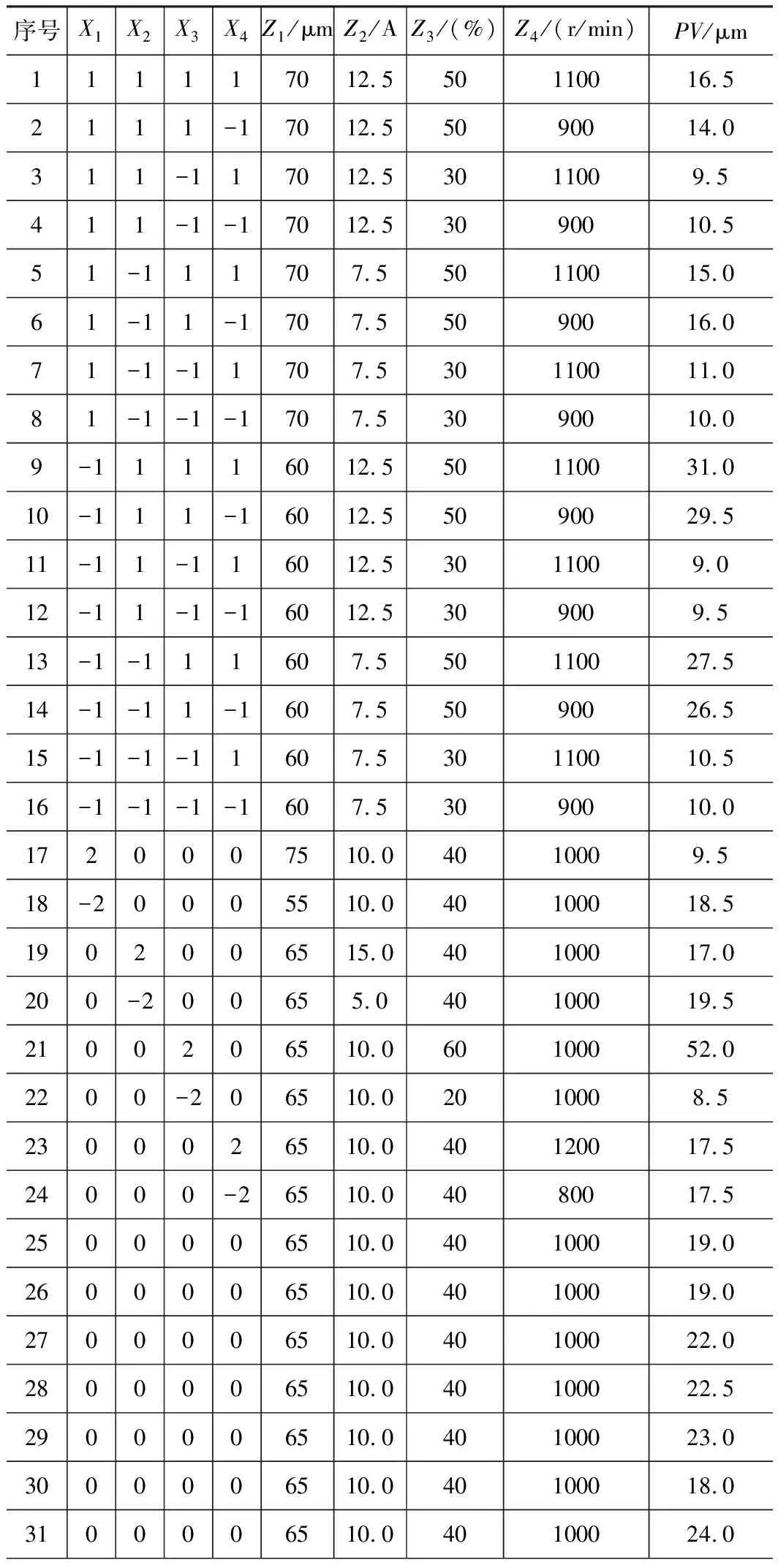
表4 二次通用回归旋转组合试验设计与试验结果
3 分析
3.1 轮廓偏差PV值二次回归数学模型建立
利用DPS数据处理系统软件对上述数据进行处理,得到轮廓偏差PV值的二次回归方程:
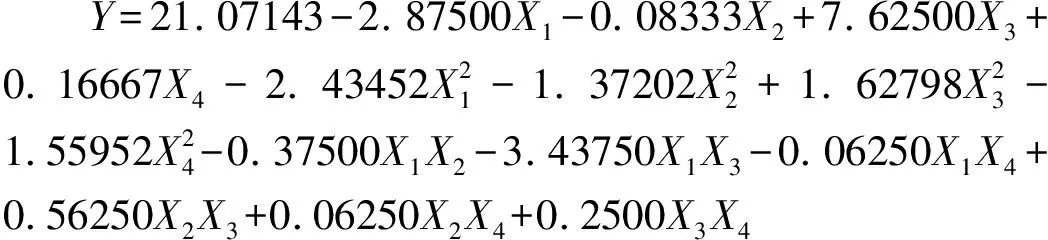
3.2 轮廓偏差PV值二次回归数学模型显著性检验
回归方程已经求出,但是判断其是否正确表述轮廓偏差PV值与4个因变量间实际存在的真实关系,还要对其进行显著性检验。利用DPS数据处理系统软件对轮廓偏差PV值数据进行方差分析,得到如表5所示的分析表。利用分析表数据,采用F检验法对回归方程进行显著性检验,采用R检验法对回归参数进行显著性检验。根据轮廓偏差PV值实验结果方差分析表得到:F3=27.981>F0.01(14,6)= 7.678,达到极显著水平,认为对各试验因子而言,回归方程结果是可靠,可以用于指导实际预测轮廓偏差PV值。回归模型的判定系数R2=0.892 1,说明回归模型中4个自变量对轮廓偏差PV值的影响为89.21%,而其他因素的影响为10.79%,证明回归方程对实际情况的拟合程度较好。
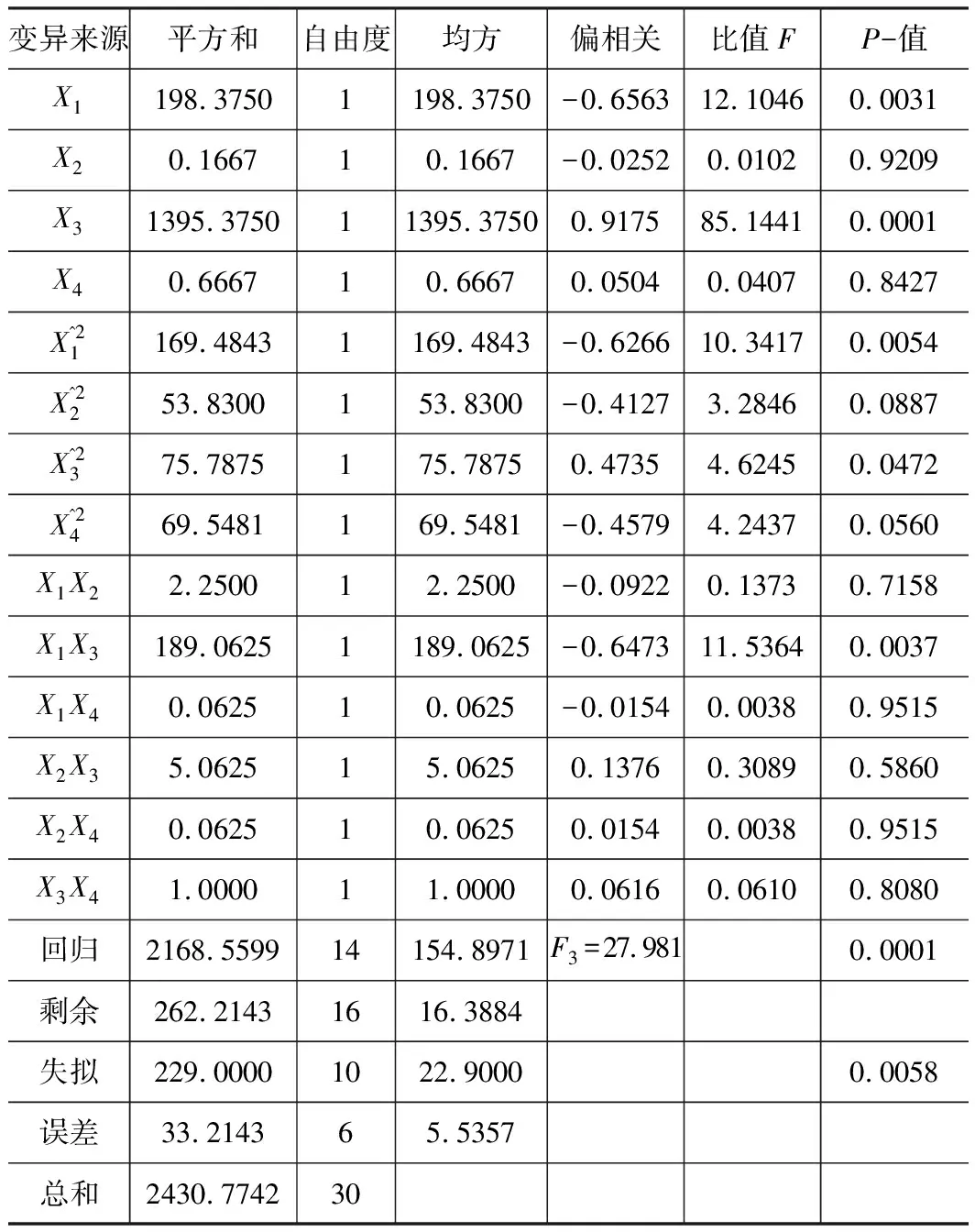
表5 轮廓偏差PV值实验结果方差分析表
3.3 金属基超硬磨料砂轮轮廓偏差PV值影响的分析
利用各因素的P值对所对应的回归系数进行显著性分析,P值越小,说明该因素对结果的影响越大。从而可以判断:各因素对轮廓偏差PV值影响大小为:脉冲占空比>放电间隙>放电间隙和脉冲占空比的交互作用>放电间隙二次项,其他的因素影响不大。
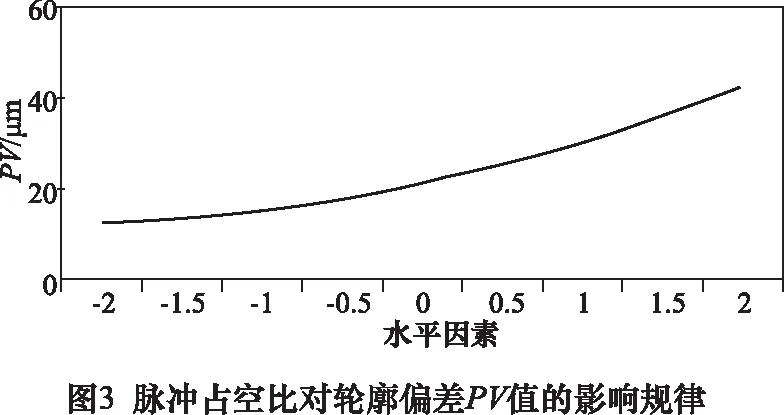
图3是利用单因素分析方法得到脉冲占空比对轮廓偏差PV值的影响规律,由图3可知,在电火花修形过程中,轮廓偏差PV值随着脉冲占空比的增大而增大,轮廓偏差PV值由13 μm增大到46 μm。在单周期内,随着脉冲占空比的增加,在有脉冲的时间段内,放出的热量增加,砂轮表面产生的凹坑加深,而无脉冲的时间段内,砂轮表面产生的凹坑基本不变,故砂轮表面高低峰差变大,破坏砂轮整体的形状,最终造成砂轮表面不平整性增加。因此随着脉冲占空比的增大,砂轮轮廓偏差PV值随之增大。
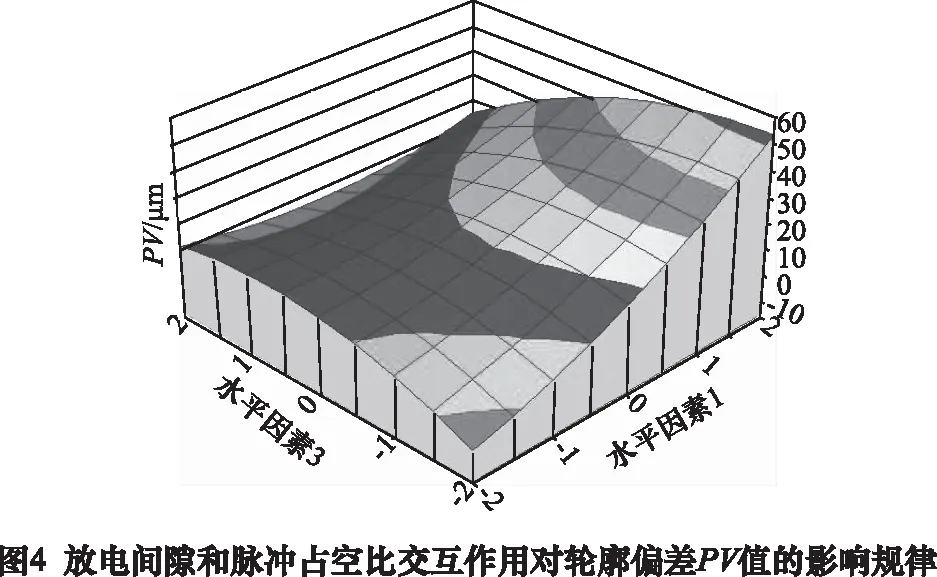
基于多因素分析法和DPS数据处理系统软件,得出放电间隙和脉冲占空比的交互作用对轮廓偏差PV值的影响规律,如图4,水平因素1代表Z1(放电间隙),水平因素3代表Z3(脉冲占空比)。由图4可知,在电火花修形过程中,当脉冲占空比较大时,放电间隙增大,轮廓偏差PV值变小,放电间隙变小,轮廓偏差PV值增大;当脉冲占空比减小时,放电间隙增大,轮廓偏差PV值变大,放电间隙变小,轮廓偏差PV值减小;并在放电间隙和脉冲占空比为最小时砂轮轮廓偏差PV值达到全局最小。该交互影响因素关系:当脉冲占空比较大时,放电间隙增大,轮廓偏差PV值变小,当脉冲占空比减小时,放电间隙增大,轮廓偏差PV值变大,该结论可指导实践生产。
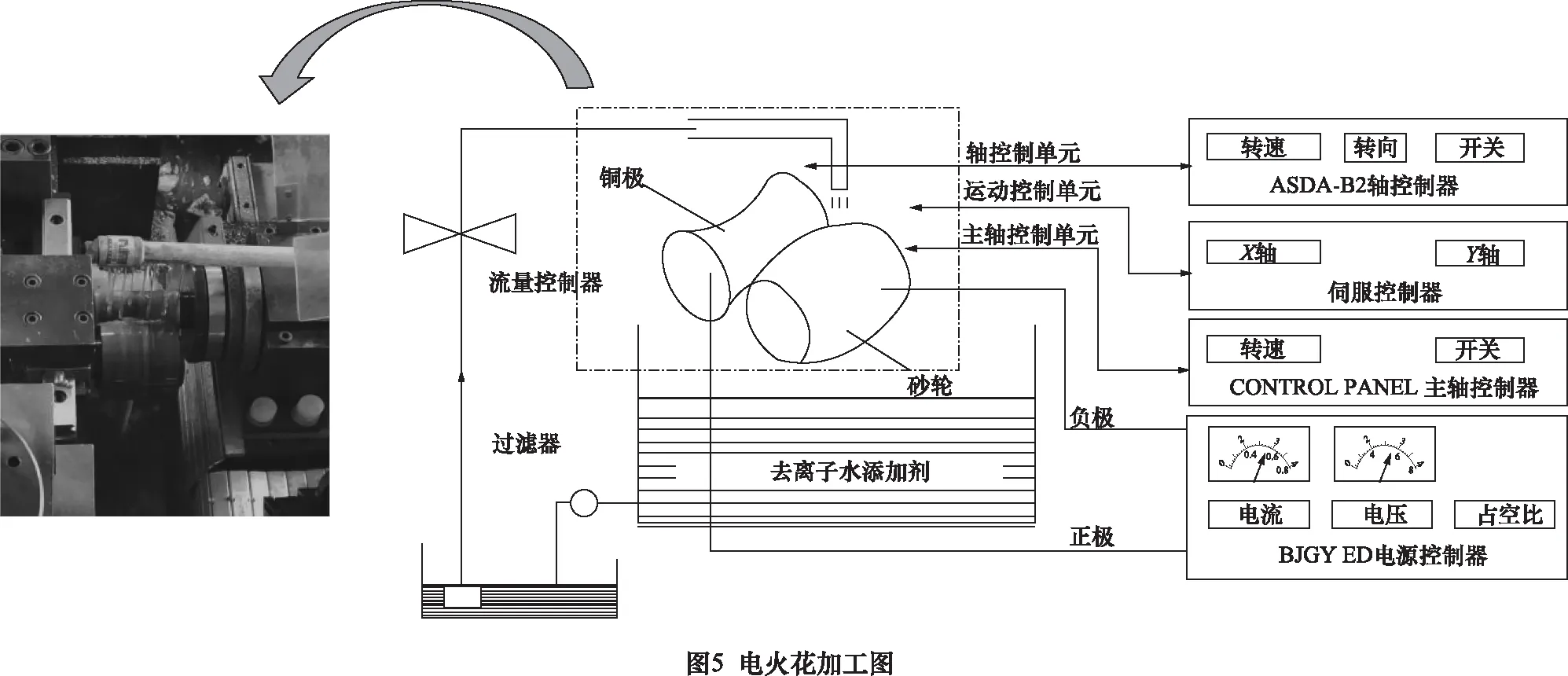
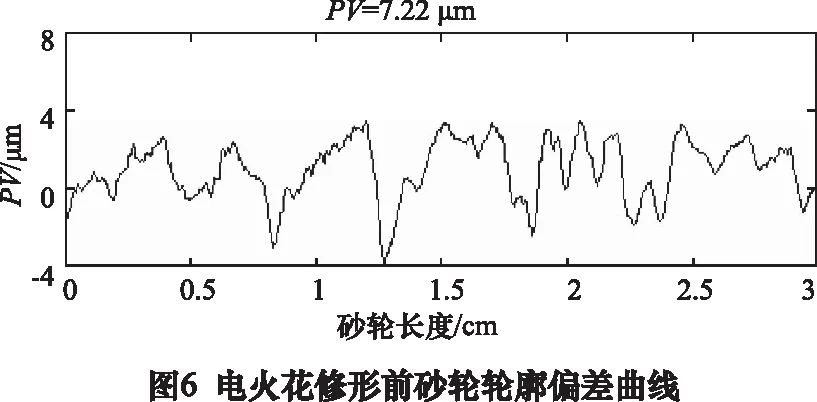
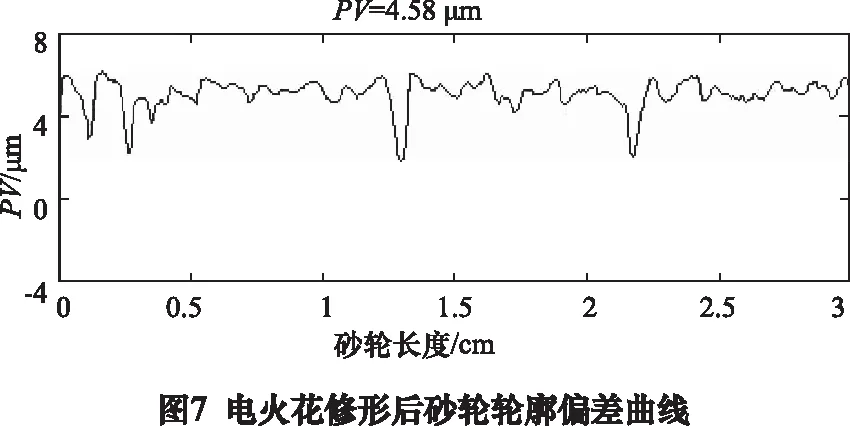
采用Lingo软件对二次回归数学模型优化得到最优参数组合为:放电间隙55 μm,放电电流15 A,占空比20%,砂轮转速1 200 r/min。以此最佳工艺参数对W40金属基超硬磨料砂轮进行电火花加工,加工过程如图5所示。根据修形前、后砂轮轮廓偏差曲线图6、图7对比,可知在此最佳工艺参数的基础上对W40金属基超硬磨料砂轮进行电火花加工,经过5 h加工后,砂轮轮廓偏差PV值降到4.58 μm后基本不变。在同样的实验条件下,采用传统“对磨法”对同样的砂轮进行精密修形,对磨8 h后,砂轮轮廓偏差PV值降到5.21 μm后基本不变,对比可知本实验方法在修形效率方面提高37%,修形精度方面提高12.09%。
4 结语
本文对弧形金属基超硬磨料砂轮进行电火花在位精密成形修形实验,得到以下结论:
(1)采用DPS数据处理系统对修形后砂轮轮廓偏差PV值的检测结果进行数据处理,获得W40弧形金属基超硬磨料砂轮表面轮廓偏差PV值的二次回归数学模型,并据此分析得到电火花工艺参数对表面轮廓偏差PV值影响作用的大小顺序:脉冲占空比>放电间隙>放电间隙和脉冲占空比的交互作用>脉冲占空比二次项。
(2)采用Lingo软件对上述模型进行优化,得到弧形金属基超硬磨料砂轮电火花在位精密修形最佳工艺参数:放电间隙为55 μm,放电电流15 A,占空比20%,砂轮转速1 200 r/min。以此工艺参数对W40弧形金属基超硬磨料砂轮进行修形,砂轮轮廓偏差PV值由7.22 μm降到4.58 μm,与传统“对磨法”相比,修形精度提高12.09%,修形效率提高37%。
