基于模拟退火遗传算法的纺纱车间调度系统

郑小虎，鲍劲松，马清文，周 衡，张良山

(东华大学 机械工程学院，上海 201620)

环锭纺纱是主要的纺纱方法，其具有流程长，生产速度高，设备多，布局复杂等特点。近年来，纺纱行业由劳动密集型产业渐渐地向自动化、智能化方向转型，但是部分典型工艺仍然难以实现自动化生产。比如在并条车间，预并到并条工序之间需要依靠人来搬运条筒。引入自动引导运输车(AGV)代替人工进行搬运是环锭纺智能工厂建设的重要手段，但引入AGV后会带来新的生产调度问题，例如需要考虑AGV与生产设备的任务匹配、AGV的运输时间分配等。通过制订合理的多AGV调度计划，可为提高企业的生产效率，降低企业生产成本提供有力支撑[1-2]。

针对AGV集成调度问题，有研究提出了一种用于求解AGV与设备集成的车间调度问题的改进花授粉算法，采用基于主成分分析法提出新的变异算子以增强算法对解空间的感知能力和跳出局部极值的能力，但该方法未考虑设备利用率[3]；为研究AGV最优调度方案和最佳AGV数量，建立使用AGV搬运的柔性车间调度模型，有学者提出了基于搬运工序、机床和AGV分配的粒子编码方式，并结合遗传算法和新的粒子群算法进行求解，达到最优效果[4]。

自动化环锭纺纱车间属于多工序、多流程的流水作业车间，多个工序存在并行机，并且为纺不同成分的纱线有时会同时执行多个工艺。根据这一特点，可以将纺纱车间调度看成是混合流水车间的调度问题。和一般流水车间调度问题相比较，混合流水车间的调度问题(HFSP)要显得更加的复杂，它是工件的排序与设备的分配问题组合[5]。HFSP是并行机的调度问题与流水车间的调度问题的结合，现已被证明是一个NP难(NP-Hard)的问题[6]。尤其是在考虑了多AGV调度问题的时候，求解难度更大。因此，如何建立合理的调度模型，并提升模型求解效率是实现纺纱车间高效运行的理论基础。多种算法都在求解中得到应用。有研究在采用多目标离散灰狼优化算法，同时考虑最大完工时间和设备负载建立了焊接调度问题的混合整数规划模型[7]；在研究并行批处理机的组批调度问题时，可将车间能耗考虑进来并以最小化最大完工时间为目标函数建立调度模型，而组批阶段采用基于FFLPT(first-fit longest processing time)和BFLPT(best-fit longest processing time)的启发式规则，最后在调度阶段采用带邻域搜索的粒子群-遗传混合算法对模型进行求解[8]；数学优化算法(TLBO算法)也可以用于求解多种车间调度问题，与其他算法对比证明，TLBO能有效求解小规模和大规模车间调度优化问题[9]；针对条筒的动态到达特性导致组批困难问题,可采用混合型蚁群算法加BATC算法对批次进行调度，以解决多产品并行批处理机调度问题[10]。针对AGV在车间装载零件过程的路径优化问题以及多AGV在路口避碰的调度问题，有研究采用改进蚁群算法建立以多AGV完成任务行驶路径最短为目标函数的数学模型，并对模型进行求解[11]。目前研究含AGV的制造车间调度问题大部分集中在解决AGV的路径规划、任务分配等问题时将AGV运输与生产设备调度分开考虑，但AGV的运输任务与设备的加工任务之间的相互影响是该类调度问题的主要考量因素。

综上所述，目前国内外对AGV生产车间协同调度方法的研究主要是采用智能优化算法进行求解，但由于目标函数不一致以及初始解的产生不一样，从而导致各种研究方法难以得到广泛的应用。基于批处理机的AGV纺纱车间主要生产瓶颈在于多种约束条件下的多目标优化问题，因为含有AGV的纺纱车间环境复杂，干扰因素众多，且各种因素相互制约，不仅要考虑AGV与纺纱设备的协同关系，还要考虑AGV与物料的协同问题，因此中间的很多工艺流程需要凭人工经验，从而导致基于批处理机的AGV纺纱车间调度模型构建难，同时也需要采用高效的求解算法提升调度效率。

本文针对基于并行机的AGV环锭纺纱车间协同调度问题，在考虑AGV与生产物料、AGV与纺纱设备之间的协同关系基础上，将影响纺纱车间协同调度的主要因素和企业目标相结合，建立了AGV纺纱车间协同调度模型，并运用智能算法对多种约束条件下的模型进行求解，从而提高基于批处理机的AGV纺纱车间整体生产效率，促进企业更加合理配置资源，提高企业竞争力。

1 问题描述及建模

1.1 问题描述

传统的纺纱车间调度问题主要考虑流水生产线和各条筒的加工状态。带有AGV的纺纱车间的生产流程主要分为3个阶段，如图1所示。

1)对棉、涤纶2种棉包进行抓包、清梳联等工序。该阶段均为自动化流水生产线，前一道工序与后一道工序之间无需通过AGV小车进行运输，也无需考虑条筒的批处理。

2)精梳、并条、混合等工序，其中棉经过精梳、预并、条并卷、精梳等工序，涤纶经过涤并工序，当棉与涤纶都完成了上述工序后，即可按照一定的比例进行混合，混合后的产品即为棉/涤混纺纤维。

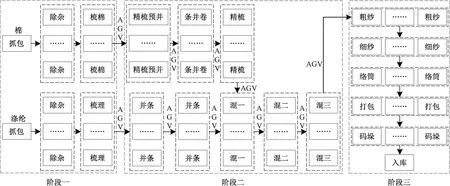
图1 环锭纺生产工艺流程Fig.1 Production process of ring spinning

3)粗细络和打包入库工序。该阶段需经历粗纱、细纱、络筒等6道工序，这些工序均为自动化流水生产线完成，只有在粗纱前，需要通过AGV小车将阶段二混合后的棉/涤混纺条子搬运到粗纱机进行批处理。

通过以上分析，纺纱车间中的AGV在进行物料搬运时会面临与纺纱设备协调的问题，尤其是当有多个纺纱设备同时生产即进行批处理时，就会产生AGV与批处理纺纱设备之间的协同调度问题。该问题可以描述为多种条筒通过AGV小车搬运，在相同批处理纺纱设备组成的平行机系统中的AGV协同调度问题。其中批处理调度又分为组批和AGV协同调度2个步骤，组批即将条筒按照一定的规则和数量分批次进行加工，AGV协同调度就是通过AGV将分批好的条筒搬运至设定好的批处理机器上进行后续的加工。

1.2 基本定义与假设

为简化AGV与纺纱机器作业协同调度问题的模型，本文做出以下合理的形式化假设与定义:

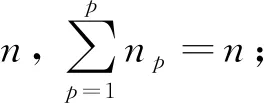
2)有m个相同的批处理粗纱机，m=1, 2,3,…,m。粗纱机可以对上述的p种产品进行加工，且p种产品中的一个条筒在纺纱设备上的加工次数不大于1；

3)有q台AGV小车，q=1,2, 3,…,q。AGV 可进行自主路径规划和导航，搬运中不同的AGV互不干扰，1台AGV同一时刻只能运送1个条筒，且AGV运送条筒的过程中不会发生故障、电量不足等其他情况导致搬运延时的现象；

4)在同一台纺纱设备上只有上一批条筒加工完之后，才可开始下一批条筒的加工，也即只能在设备空闲且能正常使用时才能接受加工任务(资源不能冲突)，在加工批处理过程中不允许中断(不允许抢占)；

5)只有同一种类产品的条筒才可以组成批次进行加工,一个批次中条筒的数量不能超过批处理纺纱设备的最大容量；因为粗纱的工艺特性，对于m台相同的粗纱机，每台粗纱机存在多个锭位，且每个锭位需对应多个条筒；

6)一台机器同一时刻只能加工一批条筒, 加工时间与该批条筒的数量无关,只与条筒对应的产品种类有关；

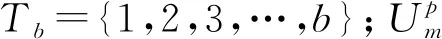
8)零时刻，所有批处理纺纱设备和AGV小车无故障，都可用。

1.3 问题建模

1.3.1 目标函数

AGV纺纱车间协同调度模型的目标函数为：

f1=min(max(Tb))

(1)

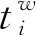
1.3.2 约束条件

与其他传统车间调度的另一重要区别在于，AGV与纺纱设备协同批处理作业车间调度不仅要考虑工艺路线约束和加工资源约束，此外还要考虑AGV小车资源和批处理的约束，为此建立以下4个约束条件：

1)工艺约束。

cn+1-tn+1-tq≥cn

(2)

式中：cn+1和tn+1分别表示条筒n+1的加工完成时间和工序完成时间；cn表示条筒n的加工完成时间；tq表示 AGV把条筒n从上一道工序运送到下一道工序的时间。

2)加工设备资源约束。对于都要在设备m上加工2批相邻条筒n和n+1，若n先n+1加工，加工设备资源约束表示如下：

(3)

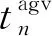
3)AGV资源约束。

(4)

式中：q表示AGV序号；ci表示AGV运送第i个任务完成时间；ti+1表示第i+1运送任务所需时间，它等于AGV路径规划算法得出的路径长度除以AGV速度。

4)批处理约束。该约束表示在有批处理加工阶段，应确保此加工阶段同一批内的条筒连续进行加工，即同一批内相邻2条筒之间不允许有空闲时间，其约束表达式为：

tn+1-tn=0

(5)

2 模拟退火遗传算法的设计

遗传算法具有适用性强、良好的并行处理能力以及运行效率高等优点，但也存在易过早收敛于局部最优解的缺点。造成算法过早收敛主要是因为伴随着种群不断进化，种群中有可能会出现少数个体的适应度值远远超过其他个体，这些个体在选择交叉等遗传操作具有很强的优势，会使种群丧失多样式。因此，本文选择将遗传算法和模拟退火算法结合，模拟退火遗传算法(SA-GA)在优化操作、原理等方面融合了模拟退火算法(SA)和遗传算法(GA)各自的特点，使得优化过程的搜索行为更加完善，增强了全局搜索以及局部搜索能力，而且能有效控制收敛过快现象的出现，理论上能较好解决车间调度问题[11]，因此，本文考虑将模拟退火和遗传算法进行结合的模拟退火遗传算法，克服遗传算法易得到局部最优解和过早收敛的问题，在提高基于批处理机的AGV纺纱车间调度系统生产效率的同时，提高生产车间设备的利用率，实现最大化企业利润。模拟退火遗传算法的设计步骤如下。

1)编码与解码。本文采用正整数编码方式，对批处理的设备和AGV进行编码，构成染色体的基因值，利用前文介绍的约束条件产生初始染色体作为初始解。解码的过程是先将染色体转化为1个有序的操作表，然后按照约束条件对各个批处理设备和AGV逐一进行筛选，从而产生调度方案。

2)确定目标函数。目标函数采取最小化最大完工时间，批处理设备平均利用率以及设备利用率(包括AGV)，设备利用率越高，通过最小化最大完工时间的多目标优化策略，使目标函数更接近实际AGV纺纱车间的需求。

3)遗传操作。选择步骤：对于在满足约束条件下的解，采用精英保留策略与比例选择方法使得适应性高的个体以更大的概率遗传下去，从而能够提高算法的效率。交叉步骤：对于选择步骤后的个体之间随机进行交叉操作并保留满足约束条件的个体。变异步骤：采用互换操作，随机使上一步解中的染色体中2个不同地方的基因进行互换。相关参数：设置种群的初始规模，一般取100～200；交叉概率Pc与变异概率Pm；最大迭代次数一般取50～200；SA的初始温度，通过式t0=-(Cworst-Cbest)/ln(Pr)确定，其中Cbest与Cworst分别为开始群体的最适应和最不适应的目标值，Pr为其相对接受概率。退温函数，即tk+1=λ×tk。λ为退温速率；状态接收函数，就是指通过概率min(1,exp(-Δ/tk))接受新值[12-14]。算法流程：模拟退火遗传算法流程如图2所示。

3 仿真实验与评估

为验证带有AGV的纺纱车间协同调度模型及其求解算法，本文以无锡经纬马山基地环锭纺纱工厂为例，基于上述建立的目标函数，分别使用模拟退火算法、遗传算法和模拟退火遗传算法对不同条筒数量进行对比计算，做20次随机仿真。参数设置：种群初始规模设置为200，最大迭代次数为100，相对接受概率为0.1，交叉概率为0.66，变异概率为0.10，退温速率为0.9，给定条筒50个，AGV 5台，为避免偶然误差，做20次随机仿真，并求得平均值，得到最优解。表1、2分别示出采用模拟退火算法(SA)、遗传算法(GA)、模拟退火遗传算法(SA-GA)后的设备利用率、最大完工时间及其算法处理时间。

从表1可知，给定条筒数50个，在相同的设备环境下，使用模拟退火算法和遗传算法进行调度求解时，批处理机设备平均利用率分别为52%和50%，AGV设备利用率分别为52%和58%，而在使用了模拟退火遗传算法进行求解以后，批处理机设备平均利用率和AGV设备利用率分别为64%和69%。结果表明采用模拟退火遗传算法，批处理机设备平均利用率和AGV设备利用率较其余2种算法至少可提升12%和11%。由此可以看出，基于模拟退火遗传算法的AGV纺纱车间协同调度模型更能有效的提高批处理设备和AGV的利用率，减少了纺纱车间的资源浪费，从而为降低成本奠定基础。

从表2可知，当条筒为50个时，在使用模拟退火遗传算法对本文的调度模型进行求解时，比单独使用模拟退火和遗传算法的最大完工时间分别减少了1 162 s和1 619 s，并且算法计算的时间也分别减少了5 s和17 s。这是因为通过合理的调度之后，AGV在运输的过程中减少了因不合理的协同调度而导致的空闲等待时间。另外，从结果还可以看出，模拟退火遗传算法的计算效率虽然比模拟退火算法的低，但是仍在同一水平。如果能大大提高可行解的质量，避免遗传算法过早的收敛而导致局部最优解的情况，还可以进一步提升其计算效率。

综上所述，基于模拟退火遗传算法的AGV纺纱车间协同调度方法，不仅考虑了交付期和最大完工时间的关系，同时还考虑了批处理设备和AGV设备的利用率，并且在求解的计算效率上也能满足相关的要求，这为解决带有AGV纺纱车间协同调度的问题提供新的思路。

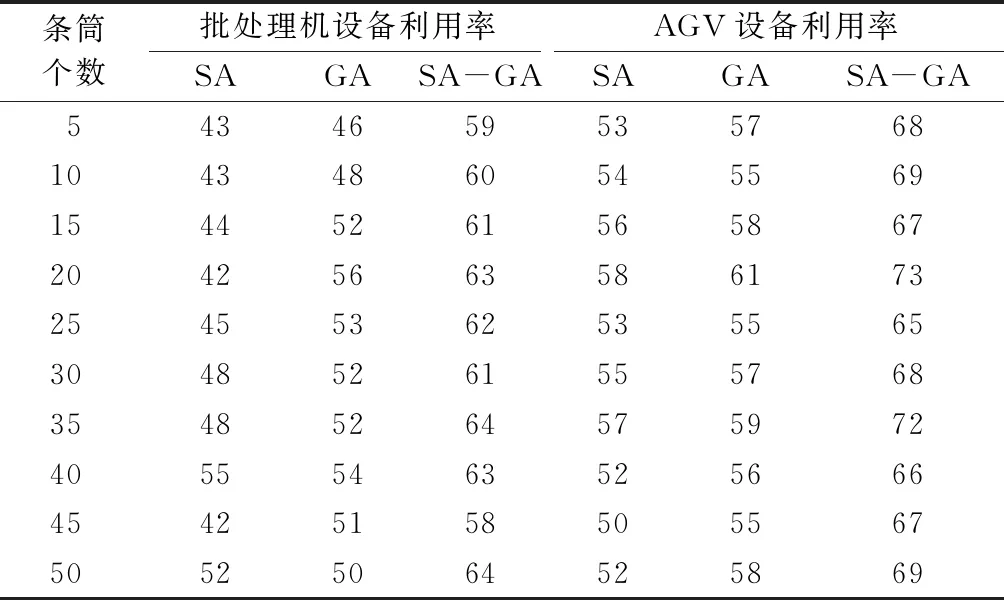
表1 设备利用率Tab.1 Equipment Utilization %

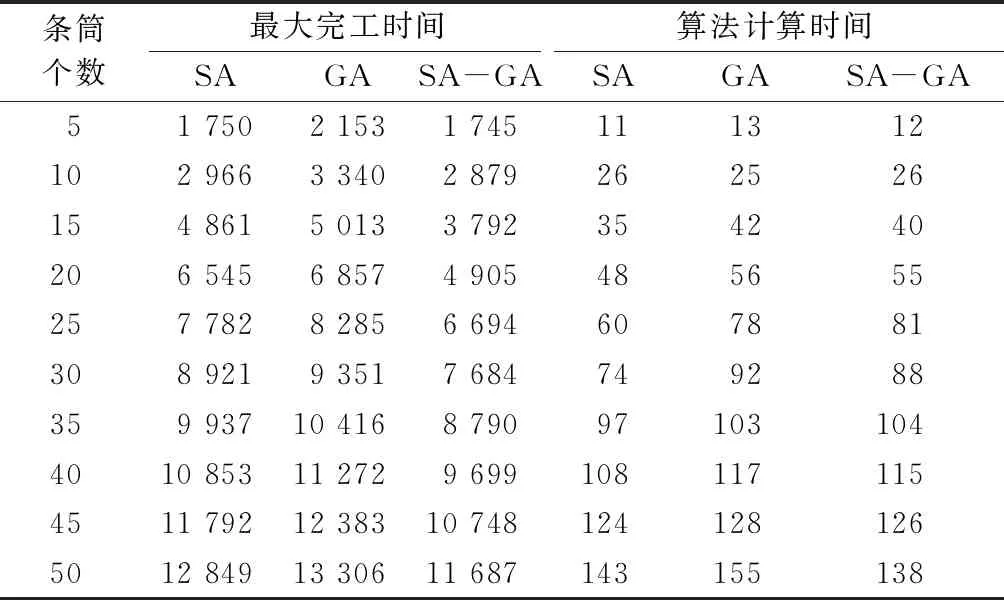
表2 最大完工时间与算法处理时间Tab.2 Maximum completion time and algorithm processing time s

4 结 论

本研究针对采用自动引导运输车(AGV)的环锭纺纱车间生产设备与AGV协同调度问题，建立了多种约束条件下调度模型并通过仿真实验验证了该算法效率，主要结论如下：

1)在考虑工艺、加工设备资源、AGV资源以及批处理4种约束的情况下，建立了满足最大完工时间最小化以及设备利用率最大化的AGV纺纱车间协同调度模型。

2)设计了基于模拟退火遗传算法的调度模型求解算法，克服了传统遗传算法易得到局部最优解和过早收敛的问题，该算法在提高基于批处理机的AGV纺纱车间调度系统效率的同时，还可提高生产车间设备的利用率。

3)以实际环锭纺纱工厂为对象，对提出的纺纱车间协同调度模型及其算法进行仿真验证。实验结果表明，当给定条筒为50个时，基于模拟退火遗传算法的调度算法要比普通的模拟退火和遗传算法的最大完工时间分别减少了1 162 s和1 619 s，纺纱车间的设备和AGV的利用率也分别提高了近12%和11%。