基于多尺度卷积神经网络的人群聚集异常预测*

罗凡波，王 平，徐桂菲，雷勇军，范 烊

(1.西华大学电气与电子信息学院，四川 成都 610039；2.国网四川省电力公司达州供电公司，四川 达州 635000；3.国网四川省电力公司资阳供电公司，四川 资阳 641300)

1 引言

当前，随着社会经济的发展，有大规模和超大规模人口的城市越来越多，这使得城市公共安全问题变得越发重要。如上海外滩与麦加朝圣发生的踩踏事件都是由于聚集行为导致人群密度过大最终造成严重的群体安全事故[1]，大城市中的地铁、车站、医院等公共区域人口密度较大，故保障其正常秩序有重大意义。在一些特定场所如城市电力变压器所在地，变压器出现问题时往往会吸引很多行人聚集围观。上述人群聚集行为易对人群的人身安全造成严重威胁，所以需要做到及时发现，及时疏散。

目前针对人群聚集检测的研究主要从以下两方面进行。一方面是通过图像处理来进行聚集异常的检测，主要是通过人数统计与人群密度估计来实现。桑海峰等[2]提出使用分布熵与运动速度来进行检测；卢丽等[3]提出改进的社会力模型，通过轨迹聚类与人群相互作用力建立人群行为模型进行聚集异常的检测；Zhang等[4]引入社会无序和拥挤属性的概念，通过在线融合策略构建了基于社会力量的群体互动模型实现聚集异常检测。上述通过图像处理的方法都存在一些缺陷，如在对人群密度进行估计时，由于行人遮挡，会导致较大误差，此外聚集行为已经发生后才能实现检测，时效性较差。另一方面是通过分析城市移动基站手机接入量、手机移动轨迹数据与试验观测统计分析建立计算模型，设立聚集异常阈值进行聚集异常判断[5]。郭玉彬等[6]提出利用分布式系统计算无线网络连接人次，通过建立中心点进行R-数索引，利用密度聚类进行聚集行为检测。通过统计模型与移动基站手机接入量来进行分析的方法，由于基站辐射区域较大，所以并不准确，且涉及一定的安全问题，故也有一定的局限性。

随着近年卷积神经网络CNN[7]在图像处理领域取得的巨大进步，各种各样的神经网络模型相继被提出[8]。文献[9]利用卷积神经网络进行车牌图像超分辨率识别；文献[10]使用快速R-CNN的选择性搜索方法和目标检测模型对车辆进行检测，目前已有的卷积神经网络能对二维图像进行有效的特征提取。本文认为应将人群聚集异常检测视为一个动态过程，首先通过改进的多尺度卷积神经网络MCNN进行人群计数，获取人群数量与坐标信息，进而计算人群密度、人群距离势能与人群分布熵这3种人群运动状态特征值，将这3种特征值送入本文提出的PSO-ELM(Particle Swarm Optimization-Extreme Learning Machine)模型进行训练预测，得到人群运动状态分类模型，最终实现聚集异常的预测。针对现有方法都是对聚集行为发生后实现的检测，本文模型能有效实现人群聚集异常的预测。本文模型的创新性主要体现在将人群聚集异常行为识别转变为动态的识别过程，通过对MCNN预测的人群密度图处理，获取较为准确的行人坐标，对人群密度、人群分布熵与距离势能进行精确的计算，与传统方法相比极大地减少了计算量且结果更为准确。

2 MCNN人群计数模型

为方便后续说明，本文人群聚集异常预测模型的流程图如图1所示，其中n为监控视频中图像帧的编号。目前人群计数方法大致分为3类[11]：(1)基于行人检测计数，通过检测视频中的每一个行人，进而得到人群计数结果。(2)基于聚类进行计数，一般使用KLT(Kanada-Lucas-Tomasi-Tracking)跟踪器和聚类的方法，通过轨迹聚类进行人数估计。这2类方法都只适用于稀疏场景中的人数统计，在人群密度较大的场景中计数相当困难。(3)回归计数方法。有大量学者对回归计数方法进行了深入研究，高斯模型回归是其中一个典型代表，但传统的回归计数在特征描述和模型建立方面仍存在一些缺陷。近年来，由于深度学习在图像处理上取得的巨大进步，许多学者通过卷积神经网络成功实现了图像有效特征的自动提取，本文所使用的MCNN能较好地解决人群密度不均、行人头部尺度不同等问题。

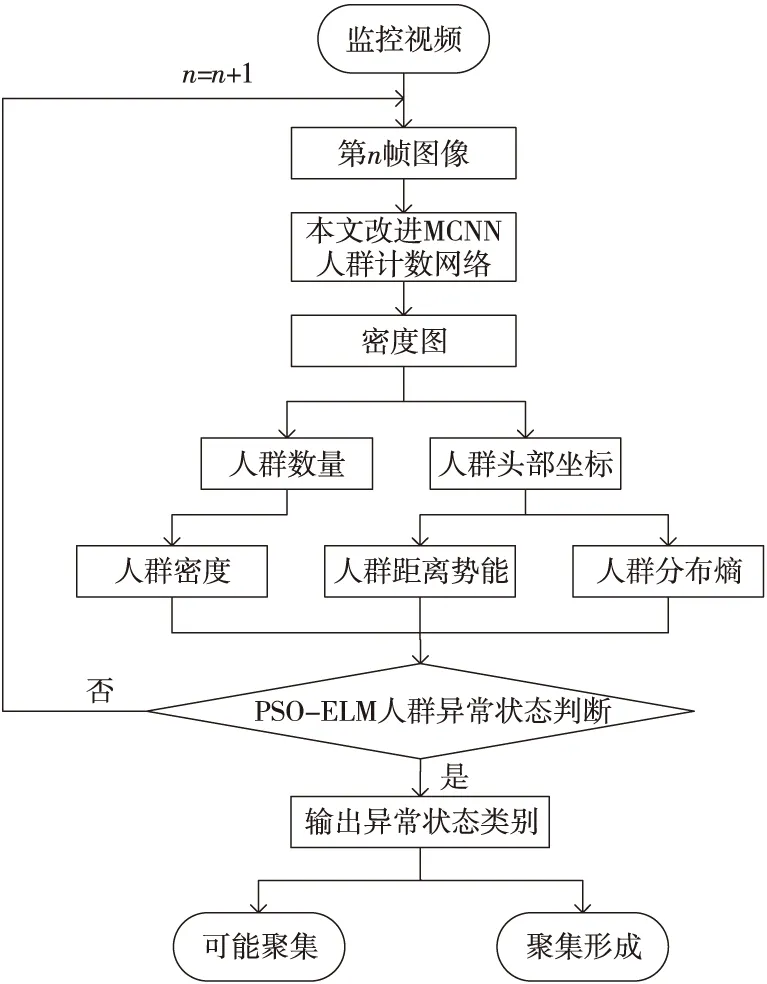
Figure 1 Flow chart of PSO-ELM model图1 PSO-ELM 模型流程图

MCNN[12]的优势在于其使用了3个卷积神经网络，不同大小的感受野能更好地应对监控图像透视[13]或图像分辨率造成的人群头部像素块大小差别的影响；另外，完全连接层被1*1的滤波器卷积层代替，这使得输入图像大小可以是任意大小，避免了图像信息的损失，网络的输出是人群密度估计图，从中可以得到人群总数。

2.1 MCNN密度图的获取

获取密度图与直接获取总人数相比具有更多优势，密度图反映了人群在图像中的空间分布，人群分布信息对人群行为分析有一定助益，因为密度越大的区域，人群越有可能发生异常行为。如本文模型检测聚集异常，就可以将人群密度大的区域作为潜在异常区域，另外，用人群密度图训练MCNN时，能让滤波器适应不同大小的行人头部，让它更适应于实际中的透视问题，提高最终人群计数的准确性。

使用标注行人头部进行密度图绘制进而训练网络并最终进行人群计数的最主要原因是，在人群密度较大的场景中，行人头部不易被遮挡，且容易被检测到，如果对人体躯干进行检测，由于躯干容易被遮挡，会导致识别效果极差，所以对于密集场景中的人群计数采用标记行人头部的方式。

本文使用几何自适应高斯核完成人群密度图参数的求解，并绘制出人群密度图。下面介绍密度图的绘制过程。若一帧图像中有N个行人头部，那么N个行人头部图像标签用式(1)进行表示：

(1)

其中，x表示像素在图像中的位置；xi表示人头中心坐标；δ(x-xi)表示人头位置；N是图像帧中人头总数。

高斯核函数为Gδ，进而获得密度聚集函数F(x)如式(2)所示：

(2)

(3)

(4)

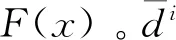
2.2 改进的MCNN网络结构

MCNN的多列网络主要是3列卷积神经网络，每一列并行子网络深度相同，每列滤波器的大小不同。本文针对行人监控场景对3列卷积核作了相应改进，其尺寸大小分为L列大尺度卷积核为(11*11,9*9,7*7,7*7,7*7)；M列中等尺度卷积核为(9*9,7*7,5*5,5*5,5*5)；S列小尺度卷积核为(7*7,5*5,3*3,3*3,3*3)，分别用于学习摄像头与人头距离较大、适中、较小的图像的特征，这使得每一列子网络具有不同大小的感受野，能让网络更好地识别不同尺寸的行人头部特征，较好地处理监控视频中存在的透视问题。最后将3列子网络的特征图使用1*1卷积核做线性加权得到最终的人群密度图。具体的网络结构图如图2所示。从图2中可以看出，MCNN的下采样系数是4，网络生成的人群密度图是原图尺寸的1/4，这使得制作的训练数据标签密度图尺寸为原图的1/4，除此之外，几何自适应高斯核也应该被限制在25个像素内。本文的网络结构主要修改了卷积核大小与网络深度，实验结果表明这些改进对行人检测很有帮助。

本文使用欧氏距离进行网络预测出的人群密度图与真实人群密度图的差值测量，损失函数如式(5)所示：

(5)

其中，NI是训练图像的数目；V(Xi,θ)是网络预测出的人群密度图；Xi是输入图像；θ是待优化的网络参数；Vi表示对应Xi的真实人群密度图。

模型评价指标使用平均绝对误差MAE与均方误差MSE，定义如式(6)和式(7)所示：

(6)

(7)

Figure 2 Structure of improved multi-scale convolutional neural network图2 改进的多尺度卷积神经网络结构图

2.3 MCNN网络训练参数

MCNN网络的具体训练参数如表1所示。训练策略一共有2 000个epoch,每一个epoch中会再有2 000次子迭代。图3是网络训练过程的MAE和MSE变化曲线。

Table 1 Training parameters表1 各项训练参数

Figure 3 Change curves of MAE and MSE during training图3 训练过程MAE与MSE变化曲线

从图3中可以看出，模型迭代至1 600次左右趋于稳定，MAE稳定在11左右，MSE稳定在26左右。

3 3种人群状态特征值计算

3种人群状态特征值分别为人群密度值、人群距离势能与人群分布熵。通过MCNN网络获取行人头部的预测位置，其与真实头部坐标有稍许偏差，但对预测结果不会有影响。通过获取的行人头部坐标，进行人群距离势能与人群分布熵的计算，人群密度值通过获取的人数进行计算。

3.1 人群距离势能计算

势能[14]是一种系统内部能量，势能是状态量，又被称为位能，可以转换为其它形式的能量，是相互作用的物体所共有的。物体的势能与初始位形(即参考位置)有很大关系。本文利用上述思想，将监控区域视为一个系统，检测到的行人作为系统内的物体，计算出每个行人的位置(即坐标)进而计算人与人之间的势能，即距离势能。

人群距离势能的计算主要是通过计算个体间的欧氏距离来确定。通过MCNN获得的每个行人个体都只有一个坐标，相较于传统算法通过多个特征角点计算欧氏距离，计算量少了很多。人群距离势能通过式(8)进行计算：

(8)

其中，Cij表示2个坐标之间的欧氏距离；φ是修正值，取常数；N为视频帧中所有行人的数目。

3.2 人群分布熵计算

熵这一概念是由克劳修斯所提出的，其在希腊语中的意义表示一个系统内在性质的改变。随后玻尔兹曼提出熵的统计物理学解释，证明了系统的宏观物理性质可以视为所有微观状态的等概率统计平均值，可以将熵看作一个系统的混乱程度的度量值。近代以来，香农将统计物理中熵的概念引入信道通信中，开创信息论学科并提出了信息熵[15]。信息熵体现了随机事件的不确定性，它对信息的多少进行了度量。本文通过信息熵来对人群分布信息进行描述，若人群分布较离散，则分布熵较大，若人群发生聚集，则分布熵较小。先将获取的行人坐标进行归一化处理为[-1,1]，再将[-1,1]划分为20个连续的小区间ri,i=1,2,…,20，再进行分布熵的计算。数学表达式如式(9)所示：

(9)

(10)

其中,S(k)是第k帧的分布熵，pi表示样本在ri区间出现的概率，count(ri)是坐标点归一化后在ri区间的个数。

3.3 人群密度值计算

计算人群密度值时，准确地获取人群的人数相当重要。传统方法一般是使用混合高斯模型提取感兴趣区域的二值前景像素，再进行角点检测获取特征角点(如使用H-S、FAST等角点检测算法)，通过特征角点计算角点密度，最后使用函数对每一帧图像中的人数进行拟合[16]；但由于人与人之间遮挡的问题，导致传统方法人数统计不准确，在耗时方面，由于有前景检测、前景像素归一化、角点检测和函数拟合等多个步骤，过程较为繁琐，耗时较多。MCNN就不存在这些问题，对每帧图像不但能输出总人数，还能输出人群密度图，这使得可对人群密度较大的区域进行特别关注，即使在有遮挡的情况下也能较为准确地统计人数。具体密度计算通过式(11)进行：

(11)

其中，density(i)是第i帧图像中的人群密度，λ是图像总人数的修正因子，Ntotal(i)是第i帧图像中的总人数，Sarea(i)是第i帧图像面积，为方便计算，本文Sarea(i)取1。

通过计算每一帧图像的人群密度，可获得人群密度变化曲线，通过曲线能获得一些人群运动状态的信息。

4 PSO-ELM在人群聚集预测中的应用

极限学习机ELM[17]是由Huang等提出的求解单隐含层神经网络的算法。ELM最显著的优点是求解单隐含层前馈神经网络时，在保证学习精度的前提下其学习速度比传统方法快得多；在算法中，输入层与隐含层的连接权值与隐含层神经元阈值是使用rand函数生成，训练过程中无需人为手动调整，只需进行隐含层神经元个数设置就能获得唯一最优解。本文将人群聚集异常这一行为视为一个动态的过程，即有正常行走、发生聚集异常趋势、聚集异常形成3种状态，将前面得到的3种人群运动状态特征数据送入PSO-ELM进行模型训练进而实现预测，判断当前人群的运动状态，预测的结果也是3种：正常行走、发生聚集异常趋势、聚集异常形成。

4.1 PSO算法原理

粒子群算法PSO[18]思想来源于鸟群的捕食行为，鸟群中的个体用无质量的粒子模拟，粒子具有速度V和位置X2个属性，速度代表搜索参数的快慢，位置代表搜索参数移动的方向。粒子在规定的区间内单独进行最优解搜寻，并将获得的最优解记为当前个体极值Pbest，将其分享给其它粒子，找到最优个体极值作为当前整个粒子群体全局最优解Gbest；所有粒子与全局最优解进行比较，进而调整自己的V和X。使用PSO优化ELM[19]后能得到更好的分类效果。本文使用的速度V的初始化范围为(-1,1)；位置X的初始化为(-1,1)；粒子群个数为250。

PSO算法的一般迭代方程[18]为：

Vi,G+1=w×Vi,G+c1×rand()×(Pi,G-Xi,G)+

c2×rand()×(Pg,G-Xi,G)

(12)

Xi,G+1=Xi,G+Vi,G+1

(13)

wi,G+1=(w1-w2)(Gi-Pg,G)/Gi+w2

(14)

其中，G为PSO迭代的代数；Pi,G为第i个粒子在前G次迭代中寻找到的最优适应值的位置信息；Vi,G为第i个粒子在前G代迭代中的速度；Xi,G为第i个粒子在前G代迭代中的位置；Gi为第i个粒子的最大迭代次数；Pg,G为在前G代迭代中种群找到的最优适应值的位置信息；w为惯性权重；c1和c2为局部和全局学习因子；w1为初始惯性值，w2为最大迭代次数的惯性值。

4.2 ELM算法原理

(1)训练集：给定Q个不同样本(xi,ti)。其中xi=[xi1,xi2,…,xin]T,为上述特征组合；ti为一个标签，表示目标属于哪一类人群。

具体应用到本文人群聚集异常预测中按下列步骤进行：

(1)针对测试集，本文模型隐含层神经元个数设置为300，对ELM分类器使用PSO进行连接权值与神经元阈值寻优；

(2)本文激活函数选取Sigmoid函数，再计算隐含层输出矩阵H;

相关实验表明[19]，在激活函数选取中，不仅可使用非线性激活函数分类非线性样本，用线性激活函数分类非线性样本，也能获得较好的效果。根据多次实验结果可知，本文使用Sigmoid函数作为激活函数能获得较好的分类效果，隐含层神经元个数根据样本集的变化而做出改变能获得较好的分类精度。

本文使用如式(15)和式(16)所示的平均绝对误差MAE与平均绝对百分比误差MAPE对PSO-ELM分类模型进行评价：

(15)

(16)

5 实验结果分析

本文模型是在普通PC机(CPU为8700K，3.70 GHz，8.00 GB内存，显卡为GTX1080，8 GB)上搭建的，MCNN是在Anaconda3+CUDA8.0+cudnn8.0.61+PyTorch1.0.1+Python3.7.3环境中进行搭建并训练测试的，训练数据集与人群运动状态特征值的计算部分是在Matlab 2014a环境中完成的;数据集方面，对人群中行人的计数使用ShanghaiTech_Crowd_Counting_Dataset中的part_B_final数据集作为训练集，测试数据集为Pets-2009中人群聚集异常数据集与自己拍摄制作的人群聚集异常数据集。

5.1 人群密度图与人群计数

MCNN预测的人群密度图与人群数量结果如图4所示，图4中每行的子图从左至右分别是监控图像、真实人群密度图、网络预测人群密度图。

Figure 4 Real density map and predicted density map of different stages of crowd massing abnormity图4 人群聚集异常各阶段真实密度图与预测密度图

图4a是在part_B_final数据集中的一幅图像，该图像是一幅人群正常行走的图像，在图像中，靠近摄像头位置的行人较为分散，故密度较低，远离摄像头的位置行人密度较大， MCNN网络预测的人群密度图与真实密度图较为接近，且网络预测的人数较传统方法有了极大的提高。图4a中真实人数为217人，预测值为220.24，与真实值相比仅仅相差3人。

图4b～图4d上面一行为Pets-2009数据集中图像，下面一行为自建数据集中图像。图4b第1行仿真图是Pets-2009中聚集异常视频片段中的第84帧，属于人群聚集异常的前期从图4b的预测人群密度图可以明显看出，此时人群分布较散，人群密度较小，与真实人群密度图反映的密度分布一致，该帧图像中真实人数为35人，预测出的人数为34.43人，仅相差1人。第2行是自建数据集，真实人数为16人，预测人数为15.78人，预测密度图也能真实反映人群密度分布。

图4c反映的是人群聚集的中后期，从密度图可以看出此时人群分布已经较为集中，Pets-2009图像真实人数为35人，预测出的人数为34.13，与真实值相差1人；自建数据集真实人数为19人，预测人数为18.92人。

图4d是人群聚集行为已经形成的情况，通过预测的人群密度图可以清楚地看到聚集中心区域人群密度较大，且与真实人群密度图保持一致，Pets-2009数据集图像中真实人数为40人，预测结果为38.35人；自建数据集图像中真实人数为20人，预测人数为19.68人。

图5所示为Pets-2009数据集中人群从正常行走到聚集异常形成过程中的人群距离势能的变化曲线。最开始由于场景中没有行人，行人从四周进入场景故其距离势能比较大，随着从四周进入的行人都往中心区域靠拢，人群距离势能开始减小；到第100帧左右，又有一定数量人群进入监控画面，随着人群进入，人群距离势能又开始变大；到124帧左右时，没有新的行人进入监控画面，此时人群距离势能开始减小，直到最后行人聚集完成，人群距离势能保持在一个较小的值。

Figure 5 Potential energy curve of crowd distance图5 人群距离势能变化曲线

图6所示为Pets-2009数据集中人群聚集过程中，人群分布熵的变化曲线。开始由于行人刚从四周进入监控画面，故人群分布熵值较大，代表人群此时较为分散，随着人群不断向中心区域靠拢，分布熵慢慢减小，到100帧左右随着新的人群进入，分布熵值开始增大，到124帧后没有新的人群进入，分布熵开始减小，一直到人群聚集完成。

Figure 6 Change curve of population distribution entropy 图6 人群分布熵变化曲线

图7所示为Pets-2009数据集中人群聚集过程中人群密度变化的情况。刚开始监控画面中只有很少的行人进入，随着时间的推移，进入监控画面的行人越来越多，故人群密度一直变大；在52帧到61帧人群密度较平稳，因为这段时间没有人进入监控区域；61帧后随着新的行人进入，密度值又开始增大，直到124帧后没有人再进入监控区域，人群密度值趋于稳定。

Figure 7 Change curve of population density 图7 人群密度变化曲线

5.2 PSO-ELM模型参数影响分析

在使用PSO算法对极限学习机ELM进行参数寻优的过程中，PSO算法的各项参数对最终的分类结果都有一定影响，如种群规模N，迭代次数iterate，初始与最大惯性权重w1、w2，局部学习因子c1与全局学习因子c2，这些参数对ELM的训练与分类精度也会造成影响，此外ELM的隐含层神经元个数H对分类结果也有较大影响。下面分析各个参数，并选出最优参数组合，作为本文模型使用的参数。

5.2.1 种群规模对分类精度的影响

设置初始种群规模为N=100，w1=0.6，w2=0.4，c1=c2=1.8，iterate=15，H=250。对于不同的N值都运行模型15次，MAE与MAPE取15次运行结果的平均值，结果如表2所示。

通过表2的运行结果可以看出，种群规模达到250左右后模型的误差评价指标变化极小，所以对于种群规模本文选取250。

Table 2 Impact of population size N表2 种群规模N的影响

5.2.2 迭代次数对分类精度的影响

设置初始迭代次数iterate=15，N=250，w1=0.6，w2=0.4，c1=c2=1.8，H=250。每取一个iterate值都运行模型15次，MAE与MAPE取15次运行结果的平均值，结果如表3所示。

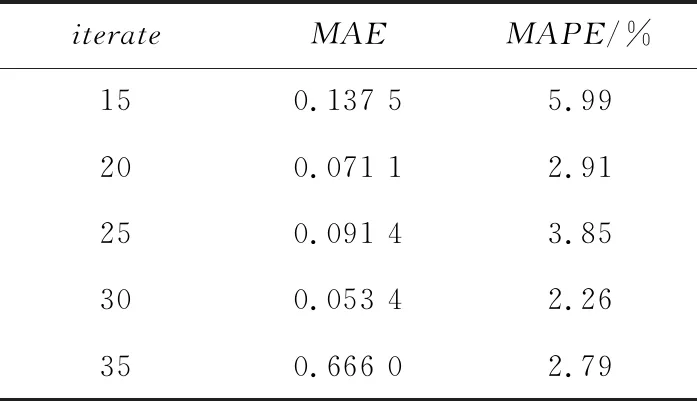
Table 3 Impact of iterations iterate表3 迭代次数iterate的影响

通过表3的运行结果可以看出，迭代次数达到30左右后模型的误差评价指标变化极小，所以对于迭代次数本文选取30。

5.2.3 惯性权重对分类精度的影响

设置起始惯性权重w1=0.6，w2=0.4，iterate=30，N=250，c1=c2=1.8，H=250。每取一个w1值都运行模型15次，MAE与MAPE取每15次运行结果的平均值，结果如表4所示。

Table 4 Impact of inertia weight w1表4 惯性权重w1的影响

通过仿真结果找到最优w1。按照上述参数设置确定w1=0.8,更改w2，每取一个w2值都运行模型15次，MAE与MAPE取每15次运行结果的平均值，结果如表5所示。

通过表5的运行结果可以看出，w2为0.5左右后模型的误差评价指标变化极小，所以对于w2本文选取0.5。

Table 5 Impact of inertia weight w2表5 惯性权重w2的影响

5.2.4 学习因子对分类精度的影响

设置起始全局学习因子c1=1.8,c2=1.2,w1=0.8,w2=0.5,iterate=70,N=250,H=250。每取一个c1值都运行模型15次，MAE与MAPE取每15次运行结果的平均值，结果如表6所示。

Table 6 Impact of learning factor c1表6 学习因子c1的影响

通过仿真结果找到最优c1。按照上述参数设置确定c1=2.2,更改c2，每取一个c2值都运行模型15次，MAE与MAPE取每15次运行结果的平均值，结果如表7所示。

Table 7 Impact of learning factor c2表7 学习因子c2的影响

通过表7的运行结果可以看出，c2为1.6左右后模型的误差评价指标变化极小，所以对于c2本文选取1.6。

5.2.5 隐含层神经元数量对分类精度的影响

本文选取PSO最佳参数组合，对ELM隐含层神经元个数进行选取，设置初始神经元个数为150个，每取一个值都运行模型15次，MAE与MAPE取每15次运行结果的平均值，结果如表8所示。

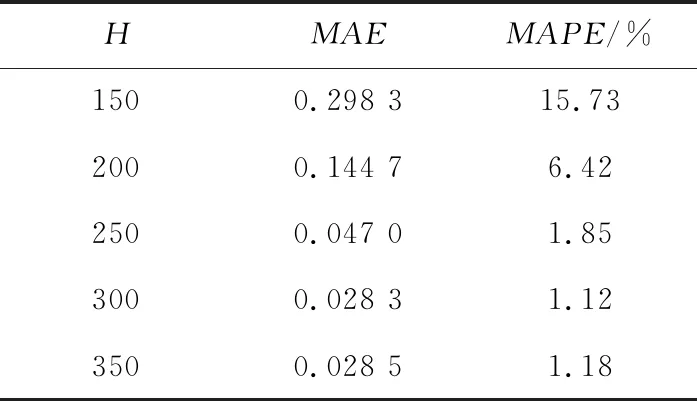
Table 8 Impact of neurons number H in the hidden layer表8 隐含层神经元个数H的影响

通过表8的运行结果可以看出，H为300左右后模型的误差评价指标变化极小，故本文模型隐含层神经元个数取300。

选取最优参数组合后进行分类模型的训练测试，实际预测结果如图8所示。

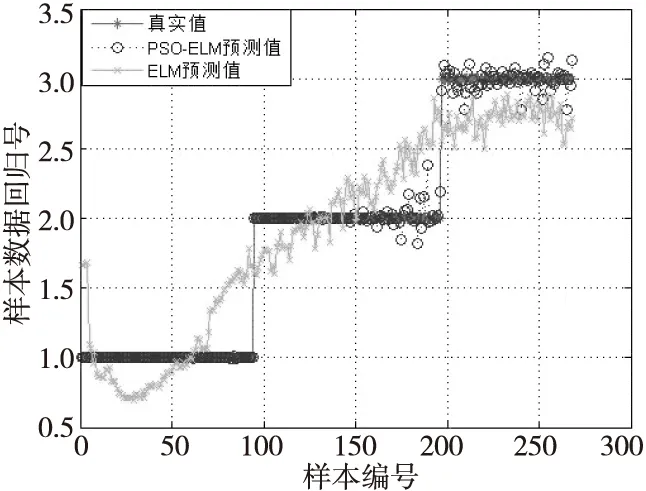
Figure 8 Prediction results of PSO-ELM and ELM图8 PSO-ELM与ELM预测结果

从图8中可以看出，经过PSO参数寻优后ELM的分类精度有了较大的提高，能准确识别正常行走、人群聚集预测、人群聚集形成等3个阶段，预测准确率达到了97.17%。相比之下ELM的预测效果就差了很多，存在很多分类错误的样本。实验表明，使用粒子群算法进行参数寻优能显著提高ELM的预测准确性。

5.3 与传统算法对比

与参考文献[3,5,20,21]中算法的人群聚集行为识别准确率对比，结果如表9所示。

Table 9 Prediction results comparison 表9 预测结果对比

表9中本文1和本文2分别为本文模型在数据集Pets-2009与自建数据集上的实验结果。从表9中可以看出，由于本文模型采用多尺度卷积神经网络解决了图像透视与行人遮挡问题，结合3种运动状态特征，从而使其对异常行为的识别率优于其它文献的算法；文献[3]通过轨迹和人群相互作用力建立人群行为模型进行人群聚集检测，由于建模较为复杂，模型参数太多，从而对最终的识别率有一定影响；文献[5]与文献[20]均利用通信基站记录的用户行为数据监测以及预测人群密度来实现检测，由于基站辐射区域较大，所得到的手机用户接入量并不准确，而且还要考虑上网行为特征与空间相关性，计算难度较大；文献[21]对目标兴趣点先聚类分组再计算聚集性，然后再提出群体聚集性描述子实现聚集检测，由于使用KLT算法，在存在行人严重遮挡情况下会产生漏检，这也直接影响了最终检测准确性。

6 结束语

本文提出了基于多尺度卷积神经网络的人群聚集异常识别模型，通过实验表明，该模型能很好的实现人群运动状态的判断，进行人群聚集异常行为的预测与识别。与传统的人群聚集识别算法相比，本文模型优势在于实现聚集异常的预测，而不是等聚集已经形成再实现检测，这对实际的生产生活场景是极具意义的，能为人群聚集异常预警与采取相应应急措施提供更多时间。因为大多群体意外事件的发生都与人群密度过大，人群聚集行为有关，如群体踩踏事件与聚众斗殴等[22]。本文完成了人群聚集异常的识别工作，未来将进一步完善目前聚集异常识别存在的不足，如当被检测图像像素过低时，对识别结果有一定影响，在暗光照条件下对异常检测也存在较大难度，这些工作将是下一步的研究重点。