受套管磨损约束的深井钻井延伸极限预测模型
2021-01-05顾岳高德利杨进黄文君石小磊周波
顾岳 高德利 杨进 黄文君 石小磊 周波
1. 中国石油大学(北京)石油工程教育部重点实验室;2. 中国石油集团工程技术研究院有限公司
随着深层油气资源的勘探开发,深井超深井应用范围和规模越来越大,特别是在我国塔里木、四川、渤海湾等盆地[1]。由于储层埋深较深(垂深4 500 m以上),深井超深井钻进过程面临地质条件复杂、井眼轨迹控制难度大等问题,从而引发严重的套管磨损[2],制约深井超深井的钻井延伸极限值。
高德利等[3](2019)指出,一口井的延伸极限受地层条件、水力条件和机械条件的制约。建立深井超深井延伸极限模型遇到如下难题:(1)未考虑套管磨损约束所建立的模型,用于指导现场作业会因忽略了套管磨损因素而造成套管磨穿等钻井事故;(2)深井超深井由于井身过长,井眼轨迹控制技术不能确保“防斜打直”的要求,井眼狗腿度会随井深增加而增大,套管易在狗腿度较大的部位磨穿,因此需要在模型中考虑深井超深井的井眼轨迹特点;(3)由井下整体管柱力学模型推导而建立的机械延伸极限模型,只关注井下钻柱,忽略了套管,若考虑套管受力,则不能从整体管柱力学模型进行推导。
针对以上问题,众多学者进行了相应研究。高德利等[3](2019)、黄文君[4](2016)基于井下整体管柱力学,建立了大位移井的机械延伸极限模型。这类模型以大位移井水平段的长度作为优化目标,以大钩载荷、管柱强度等作为约束条件,没有考虑套管磨损的约束。
Huang[5](2018)针对“三段式”井眼轨迹大位移井,初步建立了以套管磨损为约束条件的机械延伸机械模型。该模型优化目标为“三段式”井眼轨迹的水平段,而在如何延长深井超深井垂深的应用方向受限,且假设直井段无井斜。对深井超深井而言,因井身过长,井眼狗腿度会随井深增加而增大,模型需要考虑深井超深井的井眼轨迹特点。
基于套管磨损能量方程和套管磨损截面几何方程,引入套管截面磨损深度极限值,并考虑井下管柱在钻进过程中的载荷传递,采用迭代法反演出深井超深井在套管磨损条件下的延伸极限值,结合塔里木某超深井的数据资料进行实例计算,并通过和该井的井径测试数据进行对比,验证模型的合理性。
1 模型建立
1.1 物理模型
建立深井延伸极限物理模型(图1),该模型由套管与井下管柱组成,几何形状由计算井的测斜数据与井身结构决定;沿深井任意井深,做垂直于井眼轨迹的截面,得到套管磨损截面 (图 1),White等[6](1987)指出钻柱与套管之间的磨损形状为月牙形。
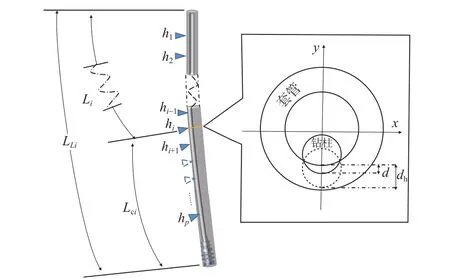
图1 深井钻井延伸极限模型Fig. 1 Deep-well extension limit mode under the constraint of casing wear
1.2 力学模型
1.2.1 套管磨损截面几何方程
套管磨损面积S的几何计算方程[2]

式中,S为某一位置处的套管磨损面积,m2;r为钻柱半径,m;R为套管半径,m;W1为磨损半宽,m;a为套管中心和钻柱中心的偏心值,m。
1.2.2 套管磨损截面能量方程
White等于1987年首次通过能量法[6]推导出套管磨损的能量方程
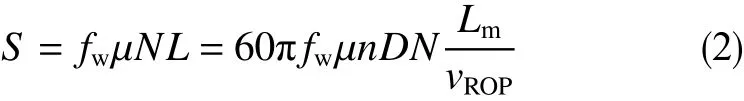
1.2.3 井下钻柱段力学模型
在式(2)中,钻柱与套管的接触力N是求得套管磨损面积S的关键。
如图2所示,深井的某井段钻柱起始点轴向力为Fi−1,井斜角αi−1,方位角i−1,终点的轴向力为Fi,井斜角,方位角φi,Huang[5](2018)由整体管柱力学理论推导出
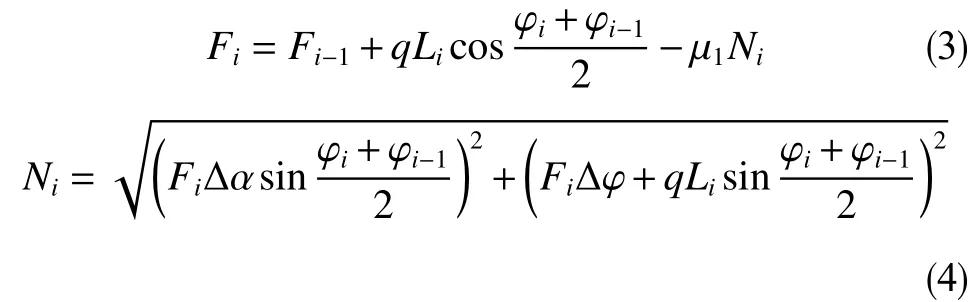
式中,q为管柱线重,N/m;为轴向摩擦因数。
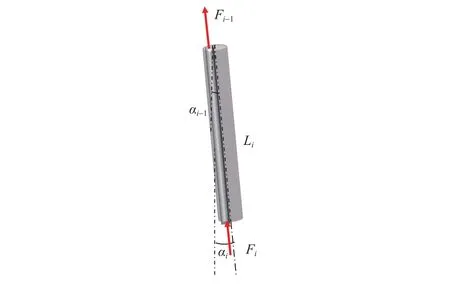
图2 深井钻柱段力学模型Fig. 2 Mechanical model of drill string in deep wells
通过迭代方程(3)与(4),可得钻柱各测点接触力Ni,从而求解出方程(2)中的管柱磨损面积S。联立式(2)与(1),未知数只有式(1)中的a,迭代计算后可以得到a的值。
1.3 数学模型
如图1所示,在套管上分布p个计算点,假设第i个计算点hi的井深为Li(i=1, 2, 3, …,p),当钻柱以hi点为起点,钻入Lci时,如果hi点处套管的磨损深度达到设定的极限值dhi,则此时的井深LLi为由点hi所决定的深井磨损延伸极限。计算出p个计算点的LLi(i=1, 2, 3, …,p)值,其中最小值为该井的磨损延伸极限。针对深井超深井狗腿角大的井段以及上部技术套管磨损非常严重处,计算点应该选择在这些部位。
dhi是已知值,黄文君[4]将其设置为套管厚度,即认为套管被钻柱磨穿是磨损延伸极限的约束条件,但是套管被磨穿前,其抗挤强度和抗内压强度会显著降低,在现场作业中,被磨损但未被磨穿的套管也容易发生变形被挤毁,从而引发安全事故[7]。关元[8]通过理论计算和数值模拟指出,当套管磨损深度超过套管厚度的40%时,套管抗挤强度和抗内压强度会显著降低,因此本文将dhi设置为套管厚度的 40%。则式(1)中的偏心值a和磨损半宽W1可由式 (5)、(6)得出
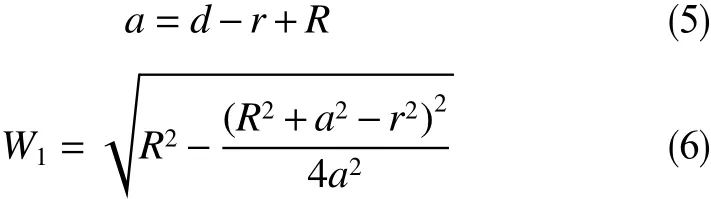
将式(5)、(6)代入式(1)可计算出当套管磨损深度为dhi时的套管磨损面积Shi,将Shi代入式(2)中可得套管磨损深度为dhi时Lci的计算式
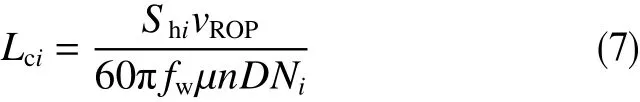
在式(7)中,Lci与Ni是未知值。钻井时钻头受到的压力设为岩石破碎压力,Ni与Lci可通过式(4)与(7)计算得来。
hi点所决定的深井磨损延伸极限LLi为

式中,Li为计算点hi所在的井深,m;Lci为计算点hi处套管磨损至极限值时钻头继续钻进的长度,m。
深井钻井深度极限模型的求解目标为
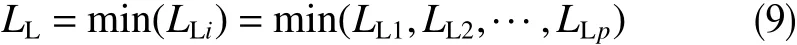
1.4 模型验证
为了验证所建立模型的准确性,采用表1塔里木7 500 m超深井的井径测试数据来进行验证。井径测试数据表明,该井磨损最严重的部位在2 900~3 100 m,这与本文模型计算出的3 000 m处套管磨损程度最严重这一情况相符合。
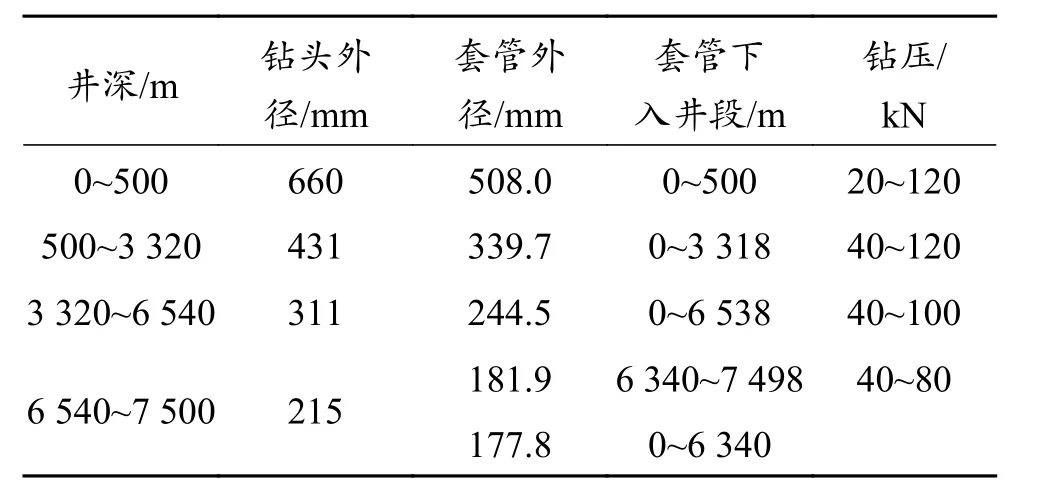
表1 塔里木案例井井身结构和各段钻进参数Table 1 Casing program of the case well in Tarim and the drilling parameters of its each section
根据现场实测井径数据,该井3 070 m处套管磨损最严重,磨损深度为3.15 mm,该处套管厚度为8.38 mm。将3 070 m井深处磨损深度3.15 mm 代入到本文模型中,即Li为3 070 m,dhi为3.15 mm,得到该井在实际套管磨损条件下的的理论延伸极限为7 812 m,与实际井深7 500 m较为接近,验证了本文模型的合理性。
2 模型应用
实例分析数据采集自塔里木油田7 500 m超深井。该井的井身结构和各段钻进参数见表1。
2.1 计算结果
计算点应选择在狗腿度大的井段以及上部技术套管处,针对该超深井2 500~4 500 m井段,每隔500 m 设置1 个计算点,共5 个计算点h1、h2、h3、h4、h5。套管磨损深度极限值dhi设置为套管厚度的40%。
将dhi和表1中井身结构参数代入到式(1)中,得到5个计算点所在井深处的套管磨损面积S,将S与表1中钻进参数代入到式(7)中,通过迭代可计算出5个计算点所在井深处的套管允许的钻进长度极限值Lci,最后通过式(8)和(9),选出这5个计算点所计算出的钻井延伸极限最小值,即为该井的钻井延伸极限,得出该井的钻井延伸极限为7 954 m。
2.2 结果讨论
由2.1节可知,只要得到深井超深井的井身结构参数和钻进参数,就能通过所建立的以套管磨损为约束条件的钻井延伸极限模型得到该深井的钻井延伸极限值。
与Huang[3]建立的以大钩载荷、管柱强度等为约束条件,垂直段长度为优化目标的机械延伸模型计算结果进行对比可知,不考虑套管磨损的钻井延伸极限计算结果为9 421 m,比以套管磨损为约束条件的延伸极限值7 954 m要大。即如果不考虑套管磨损,计算出的机械延伸极限值会偏大,如果按照该值进行钻井设计,可能会导致套管磨穿、套管强度不够等事故。
3 结论
(1)基于套管磨损理论,建立了约束条件是套管磨损的深井延伸极限模型,该模型的优化目标不再是水平段的长度,而是深井超深井的垂深。
(2)目前部分深井超深井有水平段,本文模型并未以水平段作为优化目标,因此本文模型适用性有限,下步可应用套管磨损理论,建立优化目标为水平段长度的钻井延伸极限模型。
