用离散颗粒流数值模拟方法预测气井金属网布筛管冲蚀寿命

翟晓鹏 孟文波 孔祥吉 王尔钧 黄熠 楼一珊

1. 长江大学石油工程学院；2. 中海石油(中国)有限公司湛江分公司；3. 中国石油国际勘探开发有限公司

中国南海LS深水气田储层埋深浅，储层疏松，抗压强度3.5～8 MPa，极易出砂［1］。测试井产量在(80～160)×104m3/d 之间，产出气体流速高，高速携砂气体对筛管外壳以及内部挡砂介质冲蚀严重，出现筛管破裂出砂现象，由此引起的挡砂失效问题严重影响了油气开采效率。近些年，出砂冲蚀问题越来越受到国内外防砂工作者的关注。对于气体筛管冲蚀的研究是从室内物模实验开始，利用筛管挂片质量损失率确定冲蚀速率，预测筛管寿命［2］。学者Kumar等［3］利用CT扫描分析冲蚀后筛网孔径变化，确定筛网失效标准；但实验忽略了筛管结构的影响，实验时间长，冲蚀速率计算结果误差较大。因此，有学者在室内实验研究的基础上，逐步探索利用数值模拟方法预测筛管冲蚀寿命。Greene等［4］利用CFD数模方法研究环空流速对筛管冲蚀速率的影响，建立了一个半经验冲蚀模型。Procyk等［5］通过数值模拟与实验数据对比，验证了数模求取筛管冲蚀速率的合理性，但没有给出数值求解的详细介绍。考虑筛管结构的复杂性预测筛管冲蚀寿命的数值模拟需做进一步研究。笔者考虑金属网布筛管结构特征，采用离散离子流模型(DPM)模拟砂粒流动对金属网布筛管冲蚀的影响，分析不同流体流速、含砂浓度对金属网步筛管冲蚀规律，从而预测筛管冲蚀寿命，为气井有效防砂提供理论支持。

1 气井出砂筛管冲蚀模型

1.1 气体冲蚀筛管物理模型

金属网布筛管结构从外向内由保护壳、多层筛网和基管等组成，其结构如图1所示。气井出砂后，气体携带砂粒经保护壳进入筛网，由于筛网具有挡砂作用，大部分砂粒受到筛网阻挡反弹作用，被挡在筛网外部，部分颗粒通过筛网孔隙，进入基管，流入井筒。当筛网阻挡砂粒的同时，受到砂粒的切削作用，砂粒会不断冲蚀筛网，造成筛网挡砂精度降低，防砂失效。

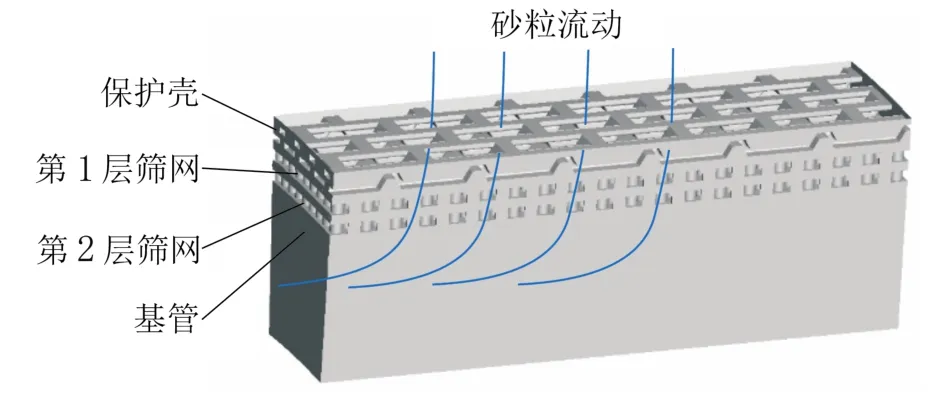
图1 金属网布筛管冲蚀示意图Fig. 1 Schematic erosion of metal mesh screen

1.2 冲蚀力学模型

气井携带砂粒冲蚀筛管过程是气固两相三维湍流问题。出砂过程中，砂粒浓度较小，因此将气固两相作为连续相处理，气体控制采用气体流动方程，砂粒运动采用颗粒运动方程，并将砂粒看作离散相处理。气体控制连续性方程和动量方程为［6］

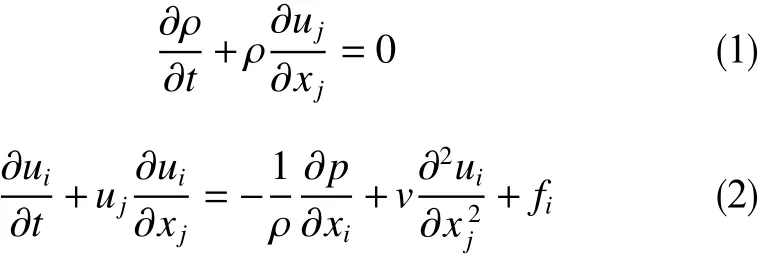
离散颗粒的作用力方程为［7］

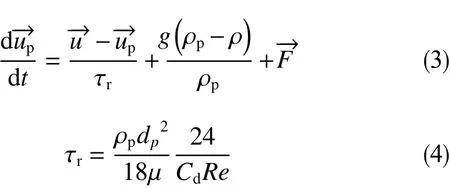
式中，ρ为流体密度，kg/m3；ui、uj为流体流速，m/s；p为压力，Pa；xi和xj为流场坐标；fi为质量力，N；为流体相流速，m/s；为颗粒速度，m/s；τr为颗粒弛豫时间，s；为重力加速度，m/s2；ρp为颗粒密度，kg/m3；为附加加速度项，N；μ为流体黏度，Pa· s ；dp为颗粒直径，m；Cd为颗粒浓度，%。

冲蚀过程中质量损失采用冲蚀速率公式为

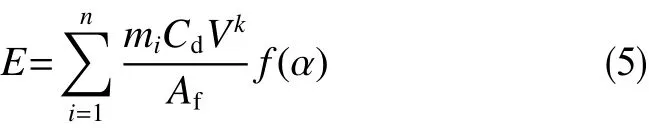
砂粒在冲蚀过程不断撞击筛网，砂粒对筛网的作用力主要是颗粒间的撞击力和砂粒对筛网的摩擦力。这个力随着冲击角度随机变化。颗粒冲击-反弹系数为［8］

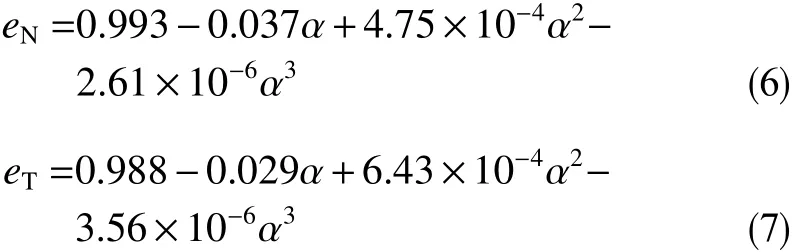
式中，E为冲蚀速率，kg/(m2· s)；mi为颗粒质量分数，无量纲；V为冲击速度，m/s；k为速度指数，无量纲；Af为冲蚀面积，m2；α为冲击角，°；eN为法向冲击-反弹系数；eT为切向冲击-反弹系数。

1.3 边界条件

气体冲蚀入口为保护壳外界面，以速度入口外边界条件，方向为网孔流道法向入口。出口边界为压力outflow。砂粒离散相与接触筛网之间的边界条件为弹性反弹。

2 金属筛布筛管冲蚀实验

为了验证模型的可行性，利用自主研发的室内气液混合流体冲蚀装置开展不同流速、含砂浓度实验条件金属网布筛管冲蚀速率实验。实验条件：冲蚀试样直接在现场筛管结构上截取，筛网挡砂精度为120 μm，筛网试样直径为2.0 cm，砂粒粒径D50为80目，砂粒浓度分别为3‰、5‰、8‰和10‰，模拟实验速度分别为0.5 m/s、1.0 m/s、1.5 m/s和2.0 m/s，模拟实验介质为空气。实验方法：混砂罐内装入一定量配置好的砂粒，利用空气泵搅拌均匀。通过空气压缩机增压，将砂粒泵入密封筒内，冲蚀筛管挂片。实验过程中每隔12 h称重一次筛网质量，确定筛网质量损失。利用冲蚀速率公式计算不同浓度和不同速度下筛网的冲蚀速率为［8］

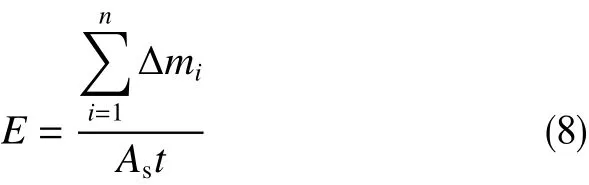
式中，Δm为冲蚀过程累计质量损失量，kg；As为试样面积，m2；t为时间，s。

每个条件下实验进行120 h，通过式(8)获取该条件下的冲蚀速率。实验结果如表1所示。

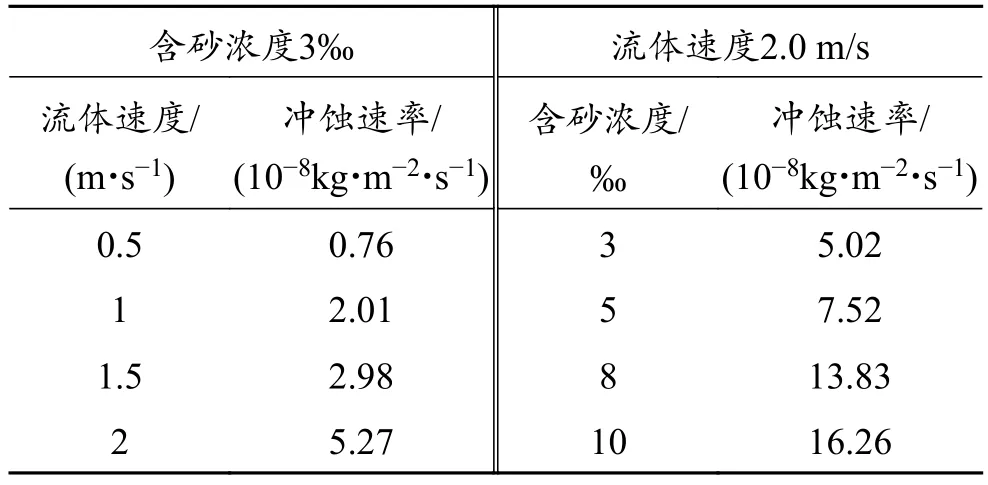
表1 不同流速和含砂浓度网布冲蚀速率Table 1 Erosion rate at different fluid velocities and sand concentrations

3 数值模拟冲蚀速率与实验冲蚀速率对比

根据筛管结构建立长×宽×高分别为10 cm×2 cm×5 cm筛管三维模型，网孔直径为120 μm，网孔交错布置。保护套流道根据筛网结构采用错位布置(图1)，分别采用与筛网冲蚀实验相同的条件，用数值模拟模型计算筛网冲蚀速率，并将数值模拟结果与实验结果对比，验证数值模拟模型的正确性。

3.1 流体速度对冲蚀速率的影响

模拟含砂浓度为3‰，模拟速度分别为0.5 m/s、1.0 m/s、1.5 m/s和 2.0 m/s，筛网挡砂精度为 120 μm。选取第1层筛网冲蚀速率平均值作为冲蚀速率计算结果，与室内气液混合流体冲蚀装置开展的不同流速、不同含砂浓度下金属网布筛管冲蚀速率实验对比。如图2所示，由不同流速下筛管冲蚀速率可知冲蚀速率随着流速增加呈现指数增长趋势，数值模拟值与实验数据的最大相对误差10%，吻合度较好。

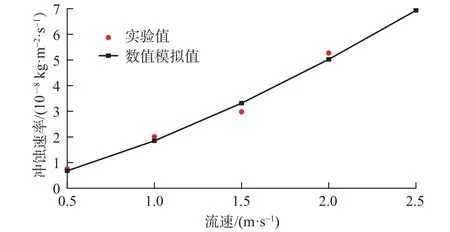
图2 不同流速下冲蚀速率数值模拟与实验对比Fig. 2 Comparison between the erosion rate calculated by numerical simulation and the experimental result at different fluid velocities

3.2 含砂浓度对冲蚀速率的影响

模拟速度为2.0 m/s，模拟含砂浓度分别为3‰、5‰和8‰，筛网挡砂精度120 μm。选取第1层筛网冲蚀速率平均值作为冲蚀速率计算结果，由不同含砂浓度下数值模拟筛管冲蚀速率与实验结果对比。如图3所示，冲蚀速率随着含砂浓度增加呈现线性增长，数值模拟值与实验数据的最大相对误差9%，吻合度较好。

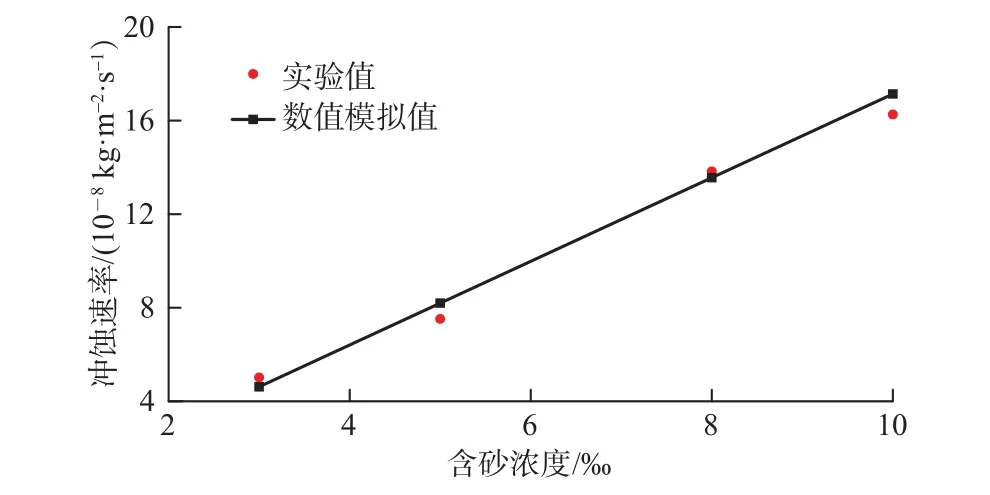
图3 不同含砂浓度下冲蚀速率数值模拟与实验对比Fig. 3 Comparison between the erosion rate calculated by numerical simulation and the experimental result at different sand concentrations

3.3 筛网结构对冲蚀速度和冲蚀速率的影响

由于筛管具有多层结构，筛管结构对筛管的流速和冲蚀速率影响较大，设定含砂浓度3‰不变，入口流速取0.5 m/s，得到筛管不同结构处的速度分布和冲蚀速率分布。根据冲蚀速度分布云图(图4)可以发现，筛管保护壳、第1层筛网和第2层筛网速度分布不同。三者之间平均速度分布依次为第1层筛网速度＞第2层筛网速度＞保护壳速度。根据冲蚀速率分布云图(图5)可以发现，冲蚀速率较大的区域集中于保护壳流道交错处所对应的第1层筛网部分。这主要是含砂流体由保护壳流道流入后，流向发生改变，多个保护壳流道流入流体集中于各保护壳流道交错处，致使该区域的冲蚀强度大幅增加，造成了冲蚀速率集中分布的情况。

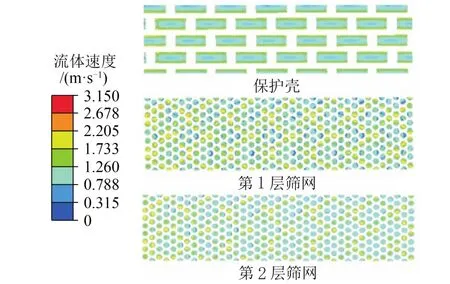
图4 入口流速0.5 m/s各层冲蚀速度分布云图Fig. 4 Cloud map of the distribution of erosion velocity at each layer at the inlet fluid velocity of 0.5 m/s

利用数模模型计算0.5 m/s和2.0 m/s时的速度和冲蚀速率分布，统计保护壳、第1层筛网和第2层筛网的平均流速和冲蚀速率平均值(表2)。由表可知，当入口流速为0.5 m/s和2.0 m/s时，第1层筛网流速是初始速度的2.32倍和4.20倍，第2层筛网流速是初始速度的1.60倍和2.10倍。第1层筛网冲蚀速率是初始冲蚀速率的10.91倍和15.96倍，第2层筛网冲蚀速率是初始速度的3.00倍和5.58倍。金属网布筛管冲蚀破坏首先发生在第1层筛网，这与现场起出的冲蚀破坏筛管所观察到的情况相符合。造成筛管冲蚀的主要原因是入口流速经过筛管结构改变，在筛网上成倍扩大，过大的流速携带砂粒冲蚀，造成冲蚀速率增大，破坏筛网。

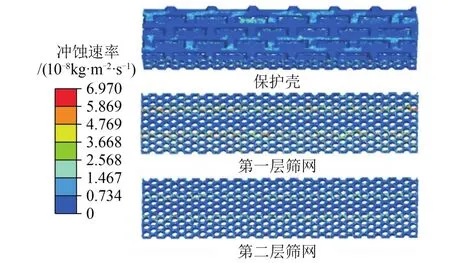
图5 入口流速0.5 m/s各层冲蚀速率分布云图Fig. 5 Cloud map of the distribution of erosion rate at each layer at the inlet fluid velocity of 0.5 m/s

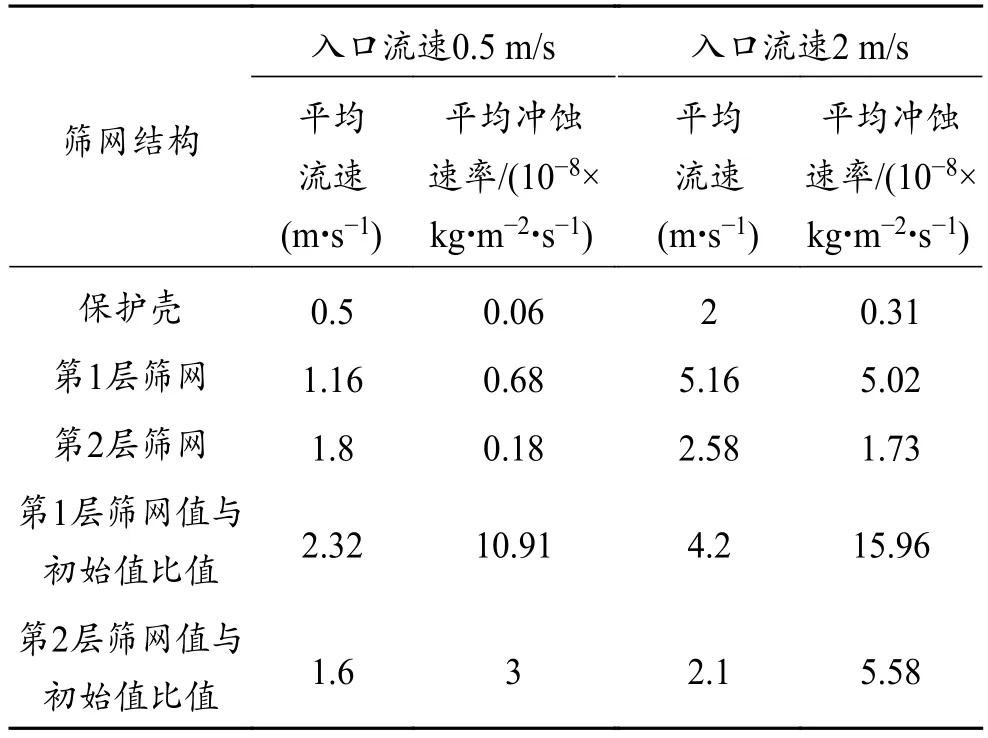
表2 筛管各层平均速度和平均冲蚀速率对比Table 2 Comparison of average velocity and average erosion rate between different mesh layers

4 工程应用

南海LS气田的水深为975～1 688 m，井深为3 321～3 351 m。LS25-X井、LS18-X井和 LS17-X井的测试产量为 60×104m3/d、100×104m3/d和160×104m3/d，而LS17-X为试采，不控制压差。井底温度 100～130 ℃，筛管外径 114 mm，挡砂精度120 μm。测试厚度 10～30 m。分别根据 LS25-X、LS18-X井和LS17-X井的产量和筛管尺寸，对流速进行换算，可得3口井入口流速分别为0.5 m/s、2.0 m/s、5.0 m/s。含砂浓度采用标准出砂率0.3‰。利用已建立的三维金属网布筛管冲蚀模型分别对不同冲蚀速度下的筛管使用寿命进行预测。以质量损失率达2%作为筛管挡砂失效的标准［9-10］。数值模拟结果现场实际监测的寿命对比见表3，可以看出，两者对比最大误差12.8%，最小误差2.0%，满足工程寿命预测需求。同时从数据结果显示可知，流速越大，筛网失效的时间越短，误差越小。

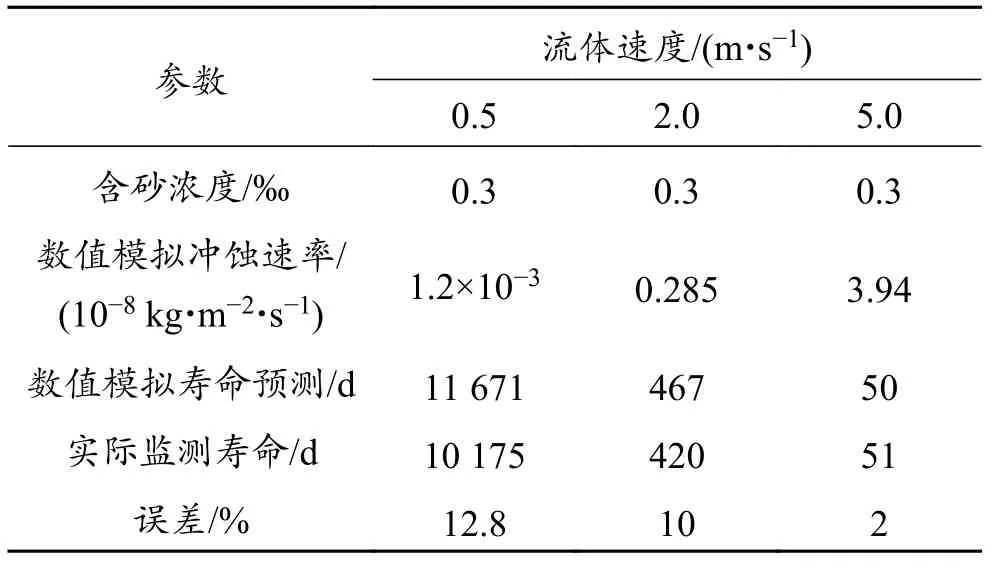
表3 数值模拟寿命预测与现场监测寿命数据对比Table 3 Comparison between the life predicted by numerical simulation and the value monitored on site

5 结论

(1)通过建立三维金属网布筛管离散颗粒流数值模拟方法预测金属网布筛管冲蚀寿命，解决了依靠实验预测金属网布筛管冲蚀寿命误差大的难题，为筛管服役寿命预测提供理论依据。

(2)筛管冲蚀破坏首先发生在第1层筛网。筛管结构导致流速和冲蚀速率比初始流速和冲蚀速率成倍扩大，这是造成筛网冲蚀破坏的主要原因。

(3)建立的三维金属网布筛管寿命预测模型考虑尺寸有限，在预测低速冲蚀情况下筛管寿命误差加大，计算模型需要进一步改进。考虑筛网堵塞情况的冲蚀模拟需要进一步研究。