改进的协同航路分配优化模型及算法研究

郭野晨风，胡明华，张 颖，谢 华

(南京航空航天大学民航学院，南京211106)

0 引 言

协同航路分配程序(Collaborative Trajectory Options Program,CTOP)用于解决航路空域内容量和流量不平衡问题.它融合了地面等待和改航两种策略，提高了空域使用灵活性.此外，它在空域资源分配上以空管为主导，考虑航空公司的航路选择偏好，具有协同决策的特征.

CTOP 优化研究可分为参数设置优化和空域资源分配优化两类，本文主要对后者进行文献梳理.模型层面：Rodionova[1]考虑了串联式飞行流量限制区的空域资源分配模型；Zhu[2-3]在模型中考虑了两次资源分配，第二次分配满足了航空公司进行时隙交换的需求；徐汇晴[4]构建两阶段模型从空管和航空公司角度优化航路资源分配.文献[3-4]仅以效率为目标，文献[1-2]虽兼顾了效率和公平性目标，但仅以加权求和的形式构造，公平性内涵不够清晰.算法层面：相关研究不多，主要围绕RBS(Ration-by-Schedule)算法展开，文献[4]提及的两阶段启发式算法就是在RBS算法的基础上加入航空公司时隙交换过程.

综上，现有CTOP研究存在公平性指标定义模糊，优化目标构造形式简单，算法效果一般等问题.对此，本文进一步研究CTOP 资源分配模型和算法.创新点为：引入基尼系数，定义衡量航路资源分配公平性的新指标；构建兼顾效率和公平的双目标非线性整数规划模型；基于特殊的染色体编码方式和满意解的选择过程，设计改进的遗传算法.

1 模 型

1.1 问题描述及条件假设

CTOP 一般运行场景如图1所示，空管下辖m个飞行扇区，其中，部分扇区(如S1和S2)受天气影响容量下降，且每个扇区均有一条可供航班选择的航路r.为确保安全，空管对各条航路设置最小飞行安全间隔λr；为充分利用空域，将允许飞经受限扇区的航班通过改航进入其他扇区.由于改航航班的加入，各扇区的延误分配情况将产生变化，因此，空管需要从整体考虑，为所有受限航班重新分配航路和延误时间.

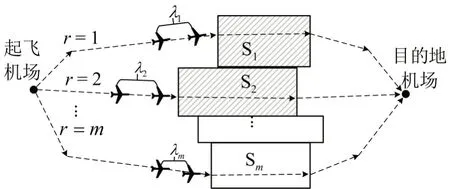
图1 CTOP 一般场景图Fig.1 General scenario of CTOP

在CTOP中，航空公司要向空管提交航路选择集，其核心内容是每个航班f对各条航路r评估的绕飞成本.在实际中，为方便管制员分配地面延误时间，绕飞成本直接以等价的地面延误时间来表示，如，其中，β为地面延误成本系数，一般令0 的航路为该航班的原计划航路.

为简化实际问题，本文假设：

(1)航路最小安全间隔一经设定不再更改；

(2)航班只受由CTOP 产生的延误，且能严格执行；

(3)CTOP分配的延误在信息及时共享下可在航班起飞前通过地面等待消耗；

(4)所有航班的地面延误成本系数一致；

(5)空管具备四维航迹预测技术，能准确推算航班飞经各点的计划时间.

1.2 模型建立

设穿越受限扇区的航路构成集合RC，穿越非受限扇区的航路构成集合RN，所有航路集合为R=RC⋃RN；飞经任意一个扇区Sr的航班构成集合Fr，其中，受限航班集合为FC，非受限航班集合为FN，所有航班集合为F=FC⋃FN.模型决策变量为df,r和xf,r，df,r表示航班f分配至航路r时的地面延误时间；xf,r是二元变量，当航班f分配至航路r时，xf,r=1，否则xf,r=0，即

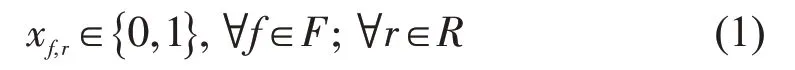
此外，决策变量还应满足

式(2)中Z 为整数集，实际航班调配间隔均以整分钟为单位，故df,r是整数变量；式(3)中df,r不得为负数，即航班不能早于计划起飞时间起飞；式(4)表示每个航班能分配到的航路有且只有一条；式(5)为容量约束，即对于选择同一航路的任意两架航班，在到达扇区进入点时，航班间的距离不小于该航路设定的最小安全间隔，其中，为航班f原计划到达扇区Sr进入点的时间；式(6)和式(7)分别表示原计划飞经不受限扇区的航班不受延误影响，且保持原计划航路选择.

在优化目标方面，本文主要考虑效率和公平性.空管将效率性能定义为总航班延误成本，但在CTOP 中，航班不仅需承受地面等待延误成本，还要承担因改航产生的绕飞成本，故单个航班f分配至航路r的成本为

本文重点研究航班延误时间的分配，故令β=1，则单个航班的校准延误为

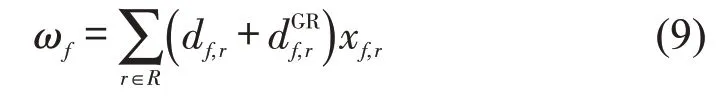
由此，本文效率目标定义为最小化总校准延误，即

空管中公平性概念较为模糊且最受争议.早期，Metron公司提出航空公司公平性评估指标[5]为

式中：da和qa分别为航空公司a的总航班延误时间和所拥有的航班数量.当ρa=1 时，航空公司a得到公平对待.根据式(11)，该公平性内涵为尽可能使所有航空公司的平均航班延误趋于一致.假设航空公司a的航班集合为，则为

ρa只能评价单个航空公司的公平性，对于系统而言，如果仅对ρa简单求和，则缺少合理性.本文引入经济学中的基尼系数，能较好地表征系统的公平性，目标函数为

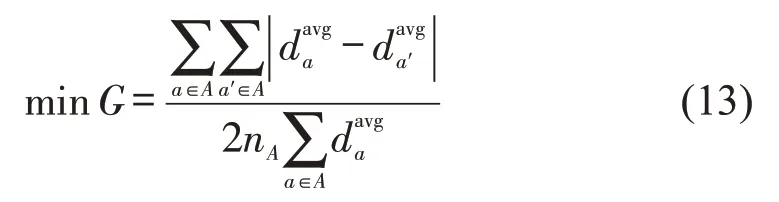
式中：A为航空公司集合；nA为航空公司数量；为航空公司a′的平均航班延误.

式(13)是使G趋于理论最小值0，也就是尽可能使各个航空公司的趋于一致，符合式(11)的公平性内涵.基尼系数还可通过构造洛伦兹曲线的几何方法表示，如图2所示，设阴影部分面积为S，则基尼系数G=1-2S.洛伦兹曲线构造方法如下：基于由小到大顺序，确定航空公司排序；基于该顺序，依次计算累计航空公司数量之和的比例和累计之和的比例；进而以前者为横坐标，后者为纵坐标，绘出nA个点；最后从原点开始依次将所有点以直线相连，近似代表理想的平滑洛伦兹曲线.当洛伦兹曲线越靠近图中的绝对公平线时，G越接近0，则系统越公平.

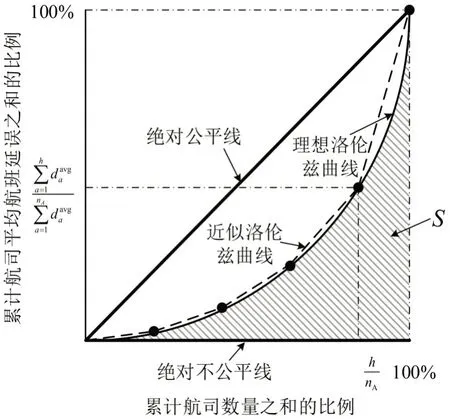
图2 基尼系数几何含义Fig.2 Geometric significance of Gini coefficient

1.3 模型分析

本文构建以式(10)和式(13)为优化目标，式(1)～式(7)为约束条件的双目标非线性整数规划模型.其中，两目标相对独立，具有同等优化地位，这不同于现有的方法，如设置权重系数关联两目标进而转为单目标问题.此外，效率与公平性目标间存在典型的悖反关系，故模型不存在最优解使两目标各自同时达到最优.

2 算 法

2.1 RBS算法

目前CTOP 主要采用RBS 算法进行求解，该算法的本质是贪心算法，具体步骤可参考文献[1].RBS 算法在确定航班分配资源优先级次序时以“先计划先服务”为准则，虽然该准则下的公平性内涵能被大多数航空公司接受，但由于这种公平性内涵无法通过清晰的指标来衡量，航空公司始终对结果的公平性感到模糊.

2.2 改进的遗传算法

根据双目标非线性整数规划模型的特点，选择第二代非支配遗传算法(Non-dominated Sorting Genetic Algorithm II,NSGA-II)求解原问题[6].

2.2.1 编码设计

由于CTOP模型含有约束条件，直接对决策变量进行染色体编码将导致染色体在变异、交叉后形成大量非可行解.可采用直接舍弃或引入罚函数的方法解决该问题，但会造成计算资源浪费.参考文献[7]，本文设计染色体为受限航班分配资源的优先级排列，即χ=(f1,f2),…,fi,…,fn，n为受限航班数量，如χ=(3,5,1,4,2)表示3 号航班第1 个分配资源，5号航班为第2个，以此类推，则算法搜索空间大小为n!.

为确保任意一个染色体能映射到一组原问题的可行解，需对染色体施加一个类似RBS 算法的贪心算法，以确保其解符合原模型中所有约束条件，如图3所示，其中，m为可选航路总数.特别地，当输入的χ是以“先计划先服务”为准则的优先级次序时，输出结果为RBS算法的结果.

图3 贪心算法流程图Fig.3 Flow chart for greedy algorithm

2.2.2 遗传操作设计

(1)选择操作(二元锦标赛法).

随机从种群中选择两个个体，比较其支配等级，等级排在前者直接获胜；若支配等级相同，再比较其拥挤度，拥挤度低者获胜；若拥挤度相同，则随机选择其一.设种群大小为nP，则选择操作重复nP遍，确保种群规模保持不变.

(2)变异操作(双点变异法).

对种群中每个个体实施变异操作前，先产生一个随机数.当随机数小于交叉概率pm时继续以下操作：随机挑选需变异的两个不同基因点，再互换其位置.如χ=(3,5,1,4,2)随机变异第2位和第5位基因点，变异后的染色体为χ=(3,2,1,4,5).

(3)交叉操作.

随机将种群中的个体两两配对，对每一对个体实施交叉操作前，先产生一个随机数.当随机数小于交叉概率pc时继续以下操作：随机产生待交叉片段的起止基因点，将两个个体的待交叉片段整段交换，由此生成的两个新个体可能存在重复基因，再对片段外发生重复的基因进行变异修正，保证交叉后的个体是不重复航班的有效排列.如染色体对χ1=(2,5,3,4,1)和χ2=(5,3,4,1,2)，待交叉片段为第2～4 位基因，初步交换后生成(2,3,4,1,1)和(5,5,3,4,2)，前者1 号航班重复，后者5 号航班重复，此时将片段外重复基因变异为缺失基因，如(2,3,4,1,5)和(1,5,3,4,2).

2.2.3 满意解选择设计

NSGA-II 将位于帕累托前沿的多个非劣解作为最终优化解集，而实际中决策者会基于对不同目标的偏好选择一个非劣解作为满意解，这一过程会因不同决策者而产生不确定性.对此，本文设计一项指标，帮助管制员从诸多非劣解中选择满意解.

鉴于RBS 算法目前在业内接受度较高，故满意解的选择应充分考虑RBS 算法的结果.Ball[8]等在提出RBD(Ration-by-Distance)算法时，通过设置偏差阈值控制RBD 算法结果与RBS 算法结果的差异程度.本文沿用该思路，设计基于校准延误的偏差指标为

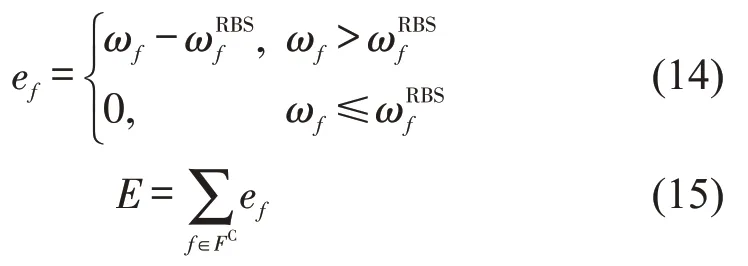
式中：是由RBS 算法得到的单个航班的校准延误.ef表示单个航班的差异，则一个非劣解与RBS算法结果的整体差异就是对所有航班的差异进行求和，如式(15)所示.最终，原问题的满意解可选择差异程度最小的非劣解.

2.2.4 整体算法分析

本文提出的改进遗传算法(如图4所示，其中，jmax为最大迭代次数)设计了基于航班优先级排列的染色体编码方式，再配合一种类似RBS 算法的贪心算法，实现将一个航班优先级排列映射至原问题中的一组可行解，确保改进算法的有效性.此外，算法末尾融合的满意解选择方法充分考虑了RBS 算法的结果，通过计算偏差指标辅助管制员决策，在一定程度上减小非劣解选择过程中的主观影响.

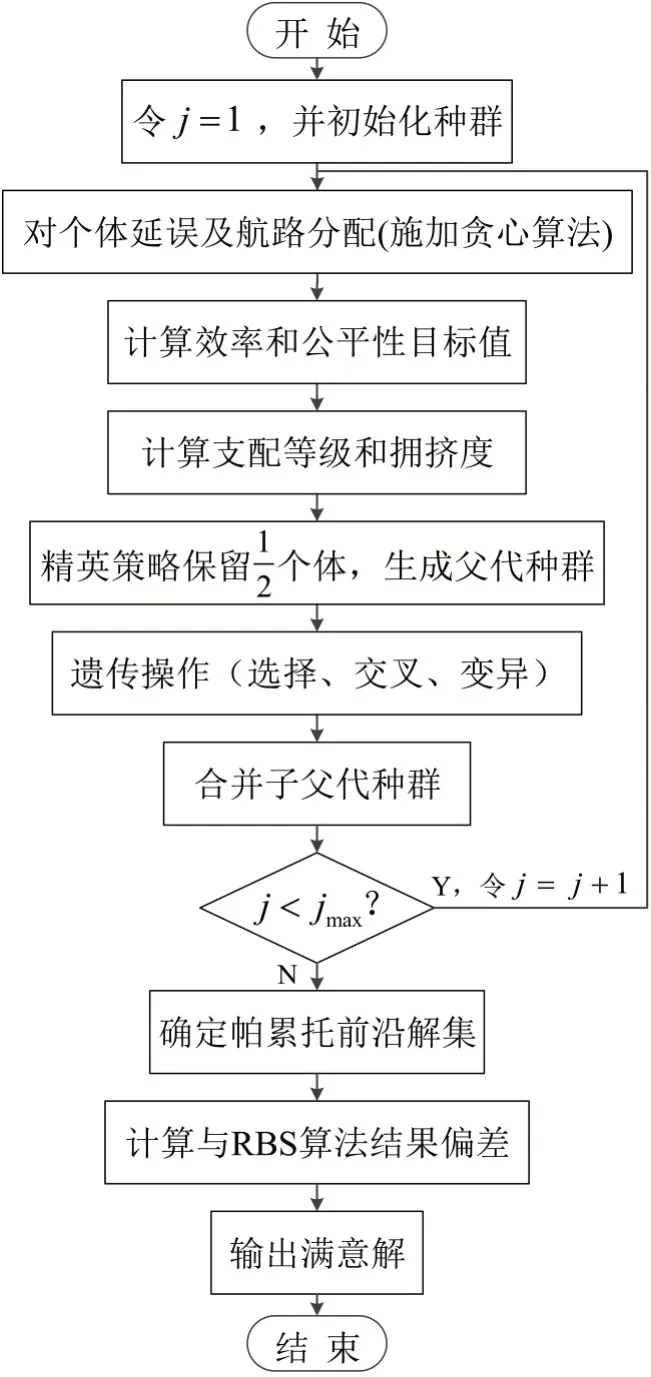
图4 改进遗传算法整体流程图Fig.4 General flow chart for improved genetic algorithm

3 仿真算例

3.1 参 数

以三亚飞行情报区作为仿真环境，如图5所示，采用该区域内部分航班计划作为仿真数据.图5中，三亚飞行情报区包含3个扇区，各自具有一条西南至东北走向的航路A202、A1 和M771，则点ASSAD、BUNTA 和DONDA 为扇区进点，点SAMAS、IKELA和DOSUT为扇区出点.实验中计算机配置为2.3 GHz i5 处理器，8 GB 内存，算法在Matlab R2017b中编写运行.

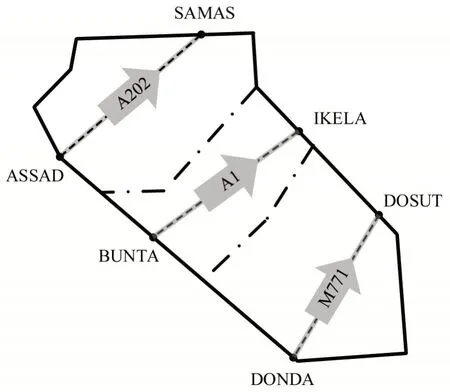
图5 三亚飞行情报区扇区及航路简图Fig.5 Air route map for Sanya flight information region

设三亚飞行情报区北边两个扇区在某一时间段容量下降，航路A202 和A1 的最小安全间隔为12 min，最南边扇区容量完好，航路M771 的最小安全间隔为4 min.该时段内受影响航班共9架，涉及5 家航空公司，限于篇幅，本文不给出具体航班参数，参数包含：每个航班所属航空公司，每个航班计划到达各进入点的时间，每个航班对每条可选航路设置的绕飞延误.改进遗传算法中参数设置如下：种群规模nP=100，最大迭代次数jmax=300，变异概率pm=0.3，交叉概率pc=0.9.

3.2 结 果

3.2.1 算法可行性验证

根据改进算法，仿真实验共得到13个非劣解，如图6中圆圈所示.为验证该结果为真实帕累托前沿，本文设计遍历算法：先找出所有可能的航班优先级排列个体，如本实验涉及9 架受限航班，整个搜索空间包含362 280个可能个体，再将这些个体输入至贪心算法，最终计算其效率和公平性目标值，如图7所示.结果发现，改进算法与遍历算法的帕累托前沿一致，证明了改进算法的可行性.遍历算法耗时1 679 s，改进算法耗时77 s，缩短计算时间95.4%，满足战术流量管理要求.实验中还记录每一代帕累托前沿解集的两个目标均值，如图8所示，结果表明，改进算法在约100 代时帕累托前沿解集趋于稳定，收敛完成.

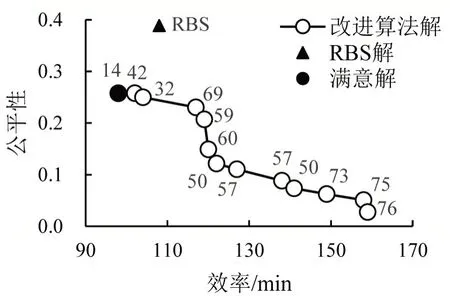
图6 基于改进遗传算法的帕累托前沿Fig.6 Pareto frontiers based on improved genetic algorithm

图7 遍历寻优结果Fig.7 All feasible solutions by enumeration

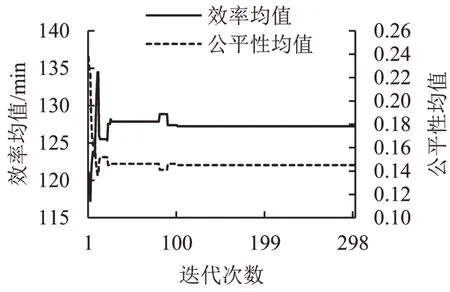
图8 优化目标曲线Fig.8 Curves of optimization objectives

3.2.2 满意解与RBS解的比较

根据文献[1]中RBS 算法流程，计算本文数据条件下的RBS 解，结果如图6中实心三角形所示.根据式(15)，计算非劣解与RBS 解的差异程度，如图6中圆圈旁的数值所示，选择数值最小的非劣解为满意解(实心圆圈).根据式(10)和式(13)，本文满意解与RBS 解的效率和公平性结果，如表1所示.相较于RBS解，满意解能提高效率9.3%，提高公平性33.7%.本文按照式(11)计算ρa，如图9所示，发现基于满意解的各家航空公司的ρa值更趋向于1.为直观展示公平性结果，绘制满意解与RBS 解的基尼系数几何含义图，如图10所示，菱形点连线为满意解的洛伦兹曲线，叉点连线为RBS 解的洛伦兹曲线，可知满意解的洛伦兹曲线更靠近绝对公平线(对角实线).

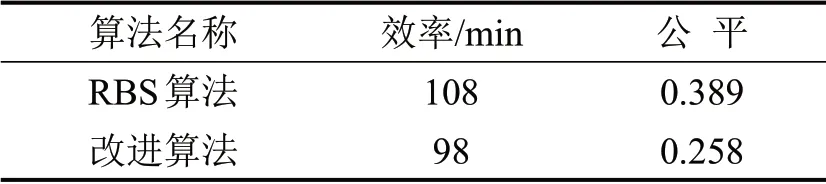
表1 RBS 算法与改进算法的结果Table 1 Results of RBS algorithm and improved algorithm

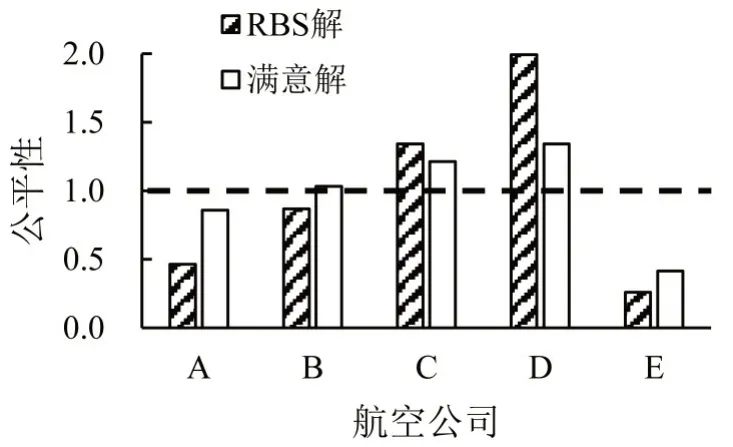
图9 航空公司公平性指标结果Fig.9 Results for airline equity metric

图10 洛伦兹曲线Fig.10 Lorenz curves

4 结 论

本文研究了CTOP 优化问题：引入基尼系数，定义可量化的公平性指标，构建以效率和公平为目标的非线性整数规划模型，采用改进的遗传算法对问题求解.仿真结果表明：改进算法能确保收敛得到真实帕累托前沿且计算时间满足战术流量管理的要求，具有可行性；改进算法中融合的满意解选择过程，能有效减小管制员选择非劣解时的不确定性影响；相比于RBS解，满意解能在效率和公平性上均得到显著优化.未来随着多效能研究的深入，CTOP 还可从稳定性、灵活性等目标进行优化，为空管提供更加全面的决策支持.