考虑续航能力的新能源汽车充电站递阶延时布局研究

谌微微，许茂增，邢青松

(重庆交通大学经济与管理学院，重庆400074)

0 引 言

《节能与新能源汽车产业发展规划(2012—2020年)》明确指出我国以纯电驱动为主的新能源汽车产业发展战略.然而，有限续航能力是影响纯电动汽车推广的首要因素.据权威数据统计，目前大部分电动汽车满电状态下续航里程约为200～300 km[1]，大多消费者将电动汽车定位为市区短距离通勤工具，中长距离出行受制于充电设施覆盖度.随着充电设施建设作为“新基建”重要领域被纳入2020年政府工作报告，以电动汽车为代表的新能源汽车基础设施科学配置问题得到政商学界的高度重视，对提升新能源汽车渗透率，改善通勤驾乘结构，实现出行绿色化、低碳化起着决定性的促进作用.因为充电设施建设存在先期风险与沉没成本，因此，保持与用户量同步提升下的分阶段有序建设，实现区域内充电站递阶延时布局优化成为有效实施新基建的关键.

充电站布局属于有限基础设施建设选址问题，国外学者主要关注模型的构建及优化，MIRHASSANI 等[2]在KUBY 等[3]提出的能源供给站截流选址模型基础上，构建网络扩展方法，可以有效提高模型计算速度，得到学界广泛认可.但该模型多基于整体优化布局，未充分考虑投资预算等因素，特别地，当需求呈现递阶增长特征时，一次性投资建设会造成巨大资金压力及资源配置效率低下，因此，ALBAREDAL S.等[4]研究多周期服务设施选址，以多周期建设为思路，CHUNG等[5]研究韩国境内充电站布局，侧重于多方法求解模型的比较；M.IRALINAGHI[6]主要从满足短距离、多时段出行需求入手，未涉及具体区位决策.国内学者杨珍珍等[7]主要研究局部区域出行需求下充电站选址；何亚伟等[8]研究不同续航里程下我国主干高速公路充电站布局策略.然而，对于严重受制于续航能力的区域中长距离出行需求，充电站多阶段布局选址及投资效率问题的研究较少.因此，本文对市区周边通过绕城高速或城际间高速的中长距离出行需求，在考虑新能源汽车续航能力约束的前提下，以消费者实际出行需求为依据，在资源有效配置的基础上，最大程度满足消费者充电需求，建立一个规划周期内多阶段的递阶延时充电站布局模型，以最大限度覆盖总交通需求，有效节约投资成本为目标；并以重庆高速公路出行需求为例进行模型求解、投资比较，以期为类似地区充电设施建设提供参考.

1 基本问题及模型描述

1.1 递阶延时布局特征

递阶延时布局在考虑续航里程的基础上，以交通流量覆盖度最大化、布局密度与投资最小化为原则，通过对路网车流统计及出行距离的分析，进行充电站多阶分布选址；在紧后阶段，依据对车流及出行距离预测，在已有布局基础上进行本阶段的充电站选址.阶延时布局示意如图1所示.

图1 递阶延时布局示意Fig.1 Multi period hierarchical layout

递阶延时布局呈现3个特征.

在空间维，以续航能力为半径的邻域衔接覆盖性.在电动汽车起始点和目的点至少需要保持1/2的电能，以确保顺利完成行程，即进行分阶段布局时需要以已有充电站为圆心，以续航能力为半径进行邻域衔接搜索，以最大限度覆盖交通流.

在时间维，随交通流密度的双螺旋同步增长性.充电站布局数量与电动汽车流量增长正相关，随着时间阶段发展，电动汽车用户增加、出行频率及出行距离增加将使充电站布局数量增加，两者相互促进，将呈现双螺旋同步增长态势.

在投资维，提高公共资源配置的有效性.若不考虑递阶延时布局，同期、同域均质化布局充电站，不仅需要巨额投资，而且容易导致充电设施资源的利用率不均衡、资金浪费与投资回收期严重迟滞等问题.空间维以续航能力为半径的邻域衔接覆盖最大化、时间维随交通流密度双螺旋同步增长的递阶延时布局可以有效降低前期投入成本，提升充电设施的可满足性和日常出行可达性.

1.2 基本模型

以MIRHASSANI 等[2]提出的截流选址模型网络扩展方法为基础，设电动汽车的最大续航里程为R；假定路网中每个起始点和目的点对(即OD对)都存在唯一最短路径，且驾驶员按最短路径行驶.与每个最短路径相关联的是出行需求、交通流和OD对.当电动汽车行驶路径经过路网中充电站时，则认为该路径被充电站覆盖，在被充电站覆盖的路径上行驶的电动汽车数量则是流量.假定路网中充电站均使用快充技术且无接待用户数量限制.模型变量设置如表1所示.

表1 变量及含义Table 1 Notation summary

假设道路网络中任意路径q上的任意两个连续节点i和j的距离dq(i,j)≤R；若dq(i,j)＞R，则需要在弧上添加节点.电动汽车电量消耗与行驶距离最相关，为保证通勤人员实现安全往返，起始点与目的点至少需要保持1/2及以上的电能，即在起始点和目的点的距离内必须至少有一个充电站.

通过在实际路网中加入源节点和汇聚节点及其虚弧，构建路网Q的扩展网络，用表示，构建扩展路网的步骤如下.

Step 1 在起始点O前添加源节点s，形成连接两个节点的扩展弧(s,O)，在目的点D后添加汇聚节点k，形成弧(D,k)，如图2所示.

它们之间的关系表示为

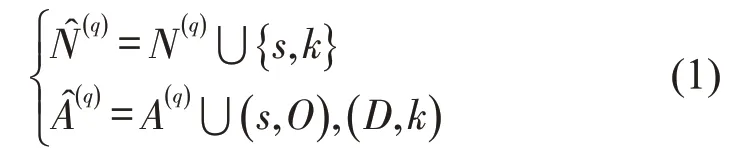
图2 扩展后路网示意图Fig.2 Schematic diagram of network after expansion

Step 2 将源节点s连接到路径q中的任意节点i，添加扩展弧(s,i)，若从起始点O在电池只有1/2电能的情况下可以达到节点i，关系式表示为

Step 3 将汇聚节点k连接到路径q任意节点j，添加扩展弧(j,k)，若从目的点D在电池只有1/2电能的情况下可以达到节点j，关系式表示为

Step 4 连接路径q中任何两个节点i、j，且节点i的排序指数小于节点j，电动汽车能在满电状态下由节点i达到节点j，关系式表示为

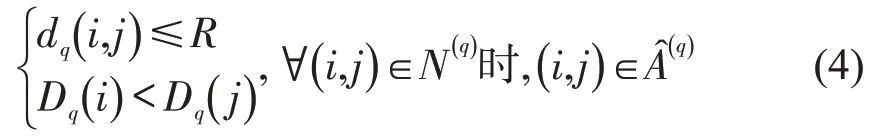
为制定最优的充电站选址规划以最大限度地覆盖总流量，对于每一路径q，引入直接连接源点s和汇聚点k的扩展弧(s,k).引入新弧集，满足.若扩展弧(s,k)的流量0，此时路径q已被覆盖；反之，若1，此时路径q未被覆盖.此外，对扩展路网添加新的约束，即

式中：m为建设充电站的总数量.

因此，截流选址模型表示为

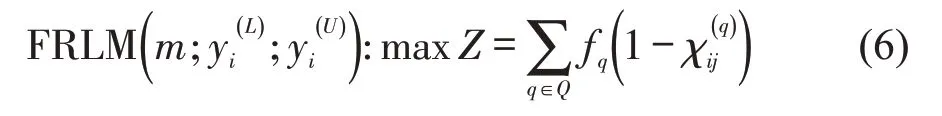
2 递阶延时布局模型

为研究新能源汽车续航能力，本文以中长距离出行需求为研究对象，以扩展的截流选址模型为基础，构建充电站递阶延时布局规划，即在给定建设充电站总数量的前提下，按照时间阶段的推移逐步建设，以最大限度地覆盖整个区域内的总流量，有效节约投资、提高资源配置效率.

以扩展的截流选址模型为基础建立充电站递阶延时布局模型.首先，建立时间阶段变量t∈T′，T′={1,2,…,T}，T为最后一个阶段.用向量n=[n1,n2,…,nT]T表示对应阶段的充电站总数量，n1为第1阶段内充电站数量，n2为第2阶段内充电站的数量，则(n2-n1)为第2阶段新建的充电站数量，(n3-n2)为第3阶段新建的充电站数量，依次类推.引入表示是否已经建立充电站的二进制变量为

式(13)表示如果某个节点i在t阶段建立了充电站，则它必须保持运行直到最后.因此，得出

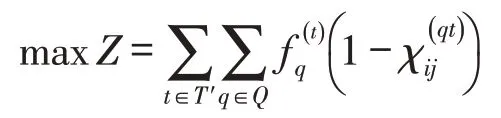
综上，多阶段充电站规划模型为

模型目标为最大限度地覆盖整个区域范围内的交通流.式(17)保证电动汽车能够经过在t阶段已经建立的充电站，式(20)确保节点一旦建立充电站就必须在剩余的阶段内保持正常运行.y(t)表示向量，

基于递阶延时建设思路，采用改进的逐步推进法，运用python3.7.4 对模型求解.假定在第1 阶段，求解FRLM(n1;0,1)得到解y(1)，即建立的充电站数量y(1)；第2 阶段，求解FRLM(n2;y(1),1)得到解y(2)，因为在第1阶段已经建立n1个充电站，故在第2阶段只建立(n2-n1)个充电站既可；以此类推，直至第T阶段.在第T阶段，求解FRLM(nt;y(t-1),1)，可知此阶段需要建立的充电站数量为(nt-nt-1).模型算法流程如图3所示.

3 案例研究

3.1 案例介绍

截至2018年底，重庆高速公路网络总里程为3 096 km，所有高速公路都是互相连通的，不考虑通行经济性和最短行驶路径时，驾驶员可以通过任意收费站到达高速公路网络中的其他收费站.此外，任何一对起始点和目的点收费站间OD 交通流量可以获取.为准确表示高速公路交叉口的车辆流向，引入额外的弧，使构建路网包含所有可能的行驶方向，如图4所示.

图3 模型算法流程Fig.3 Flow chart of model algorithm

图4 路网中交叉口节点及弧表示方法Fig.4 Representation of intersection in road network

根据上述模型，构建具有268个节点和448条无向弧(896 条有向弧)的虚拟道路网络.如图5所示.其中，每个节点代表1个收费站.

图5 重庆市2018年高速公路网络图Fig.5 Chongqing expressway network in 2018

根据重庆高速公路2018年通行数据，对于任何OD 对，存在路径及相关的交通量.若将同一OD对间所有路径的交通流组合起来，最短路径出行选择下路网中路径总数为71 824.其中，每个OD对对应1条路径.重庆绕城以外高速公路交通流量数据如表2所示，日均交通量100辆以内的路径比例为98.84%.

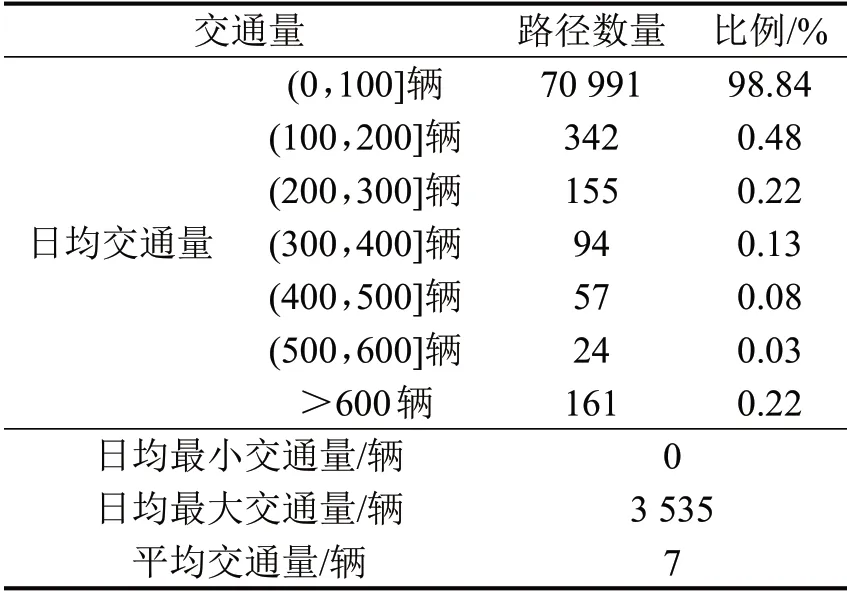
表2 2018年重庆高速公路日均交通量分布Table 2 Distribution of daily average traffic volume of Chongqing expressway in 2018

2018年重庆高速公路日均交通量如图6所示.由图6可知：[50,100]km、(100,200]km 的出行需求占比分别为21%、8%，新能源汽车渗透率仅为0.6%，在此种新能源汽车出行规模下不宜一次性建设，应根据消费者出行需求分阶段建设，保证有限续航能力约束下便利出行，逐步提高新能源汽车渗透率，使新能源汽车交通流量与充电站数量呈现双螺旋同步增长.

3.2 结果分析

以重庆高速公路2018年交通流量数据为例，用python3.7.4 求解递阶延时规划模型.不失一般性，设电动汽车年平均增长率为30%[5]，T′={1,2,3,4,5}，分别取续航里程R为200 km、300 km，充电站布局结果分别为：n=[1 1,22,33,44,55]T、n=[9,18,27,36,45]T，在ARCGIS 10.2中呈现，如图7所示.

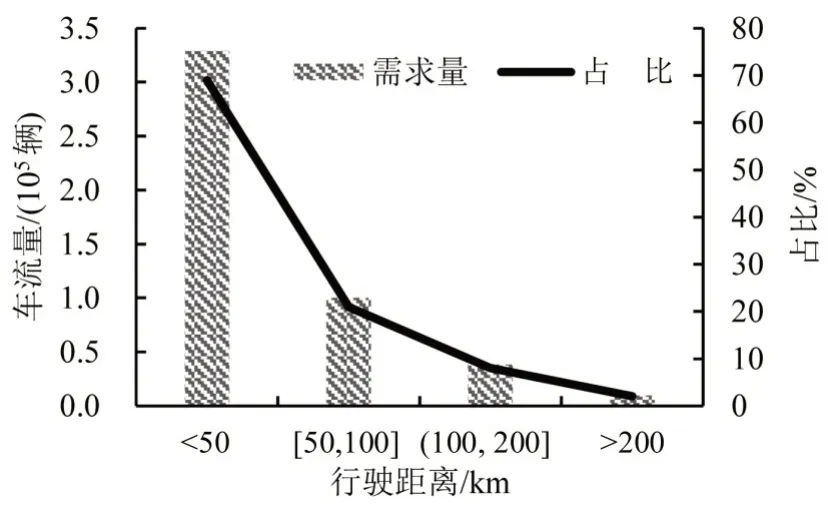
图6 2018年重庆高速公路日均交通量Fig.6 Average daily traffic volume of Chongqing expressway in 2018

图7 重庆高速公路充电站递阶延时规划布局图Fig.7 Hierarchical delay planning layout of Chongqing expressway charging station

续航里程分别为200 km、300 km时，保证中长距离出行需求覆盖不低于70%交通流的情况下，充电站建设总数分别为55个、45个，每个阶段建设数量分别为11个、9个.续航里程增大时，建站总数量将减少；此外，不同续航能力下的规划布局中存在建站选址重合，共计14个，如图7中菱形小框标识.且重合时段主要集中在第1、第5 阶段.原因在于：第1阶段充电站选址主要满足现阶段消费者出行需求，紧后的几个阶段在第1阶段选址的基础上根据续航里程进行布局，续航里程的变化导致第2～第4阶段选址出现较大变化；第5阶段的布局位置较为偏僻，甚至位于省、市交接处，选址变化相对较小，进一步凸显递阶延时布局的必要性

按照10 台充电机的充电站进行测算，每个充电站基础设施建设、配电设施成本及每年运营成本分别为300 万，200 万，20 万元，相较同期、同域均质化投入布局，不同续航能力约束下递阶延时布局可以节约的总投资如图8所示.

由图8可知：不同续航里程约束下的充电站递阶延时布局投资测算，分阶段递阶延时建设可以有效节约投资，且资金成本越高效果越明显；续航里程增加可以减少充电站建设数量，相同资金成本下续航里程的增加可以减少建站资金投入，因此，提高新能源汽车续航里程是非常必要的.

图8 重庆高速公路充电站投资测算Fig.8 Investment calculation of Chongqing expressway charging station

4 结 论

本文在考虑新能源汽车实际续航能力约束的基础上，针对市区外高速公路中长距离出行，综合考虑充电设施布局的覆盖度和完备度，构建充电设施递阶延时规划布局模型；基于2018年重庆高速公路路网状况建立具有268 个节点和448 条无向弧(896 条有向弧)的虚拟路网模型，结合实际交通流数据对不同续航里程下的布局结果进行检验.结果显示：续航里程变化会引起5个规划阶段内递阶建立充电站数量和位置发生变化，在不同的资金成本下投资支出节约程度不同，验证了模型的合理性和有效性.