基于行程时间影响的关键路段识别与查找

李君羡，吴志周*，沈宙彪

(1.同济大学道路与交通工程教育部重点实验室，上海201804；2.上海市城市建设设计研究总院(集团)有限公司，上海200125)

0 引 言

关键路段指容易发生交通拥堵或其失效后对局部路网通行效率造成较大影响的路段，常和路网脆弱性相关.基于此定义，大量研究着眼于路网失效状态，如交通事故、道路中断下的路网运行情况变化，从而识别关键路段，如张建旭[1]以路段失效后交通流在局部路网重分配情况为基础，确定不同时刻的路段关键度；也有学者从路网结构和路段位置关系入手查找拓扑结构中最重要路段，如苏飞[2]等以时空相关函数表达不同延迟下路段交通状态之间的影响，并作为路段重要性的衡量指标.

Sullivan[3]指出，在路段通行能力削弱程度不同时关键路段排序也不相同，在极端条件下筛选出来的关键路段不具代表性.且日常交通拥堵很少造成路段完全失效，发生拥堵的路段反而聚集大量通行需求；完全基于路网拓扑结构识别关键路段常基于假设或模型描述路段间的交通影响，和实际情况有一定差距.此外，现有研究多基于路段数少于20 条的小型路网结构，在大规模路网的实施效果难以保证.有研究利用路网实际数据，从路段在交通活动中实际承担的功能出发研究路段重要性，如Othman等[4]基于事故数据，研究事故高发路段的交通特性从而确定关键路段.这类研究由真实数据驱动，目的在于查找一般状态下对路网交通参数产生关键影响的路段，对路网效能管理与提升更具指导意义.本文沿用这一思路，利用真实大规模路网数据，基于对路径行程时间的影响识别关键路段，并以识别结果为参考，结合路段行程时间特性等建立关键路段判别模型，实现主动查找关键路段.

1 研究区域与数据预处理

数据覆盖上海市外环内地面路段共2 884条，长度分布集中.由浮动车于2008年9月17日全天持续采集.经地图匹配和聚合统计，形成时间间隔为5 min 共288 个时间段的路段平均行程速度；另有数据表记录各路段长度、起终节点编号与坐标位置、所在道路等级.以时间间隔序号为列索引，以路段编号为行索引构建路段平均行程速度矩阵SA，其(i,j)元sij为第i条路段在第j个时间间隔期间的平均行程速度.图1为统计数据缺失情况.

午夜城市道路交通流多为自由流，如路段首、末端速度中仅有一端值缺失，则以另一端值补全；若两端值同时缺失，以当日该路段最大速度补全.其他缺失做线性插补.

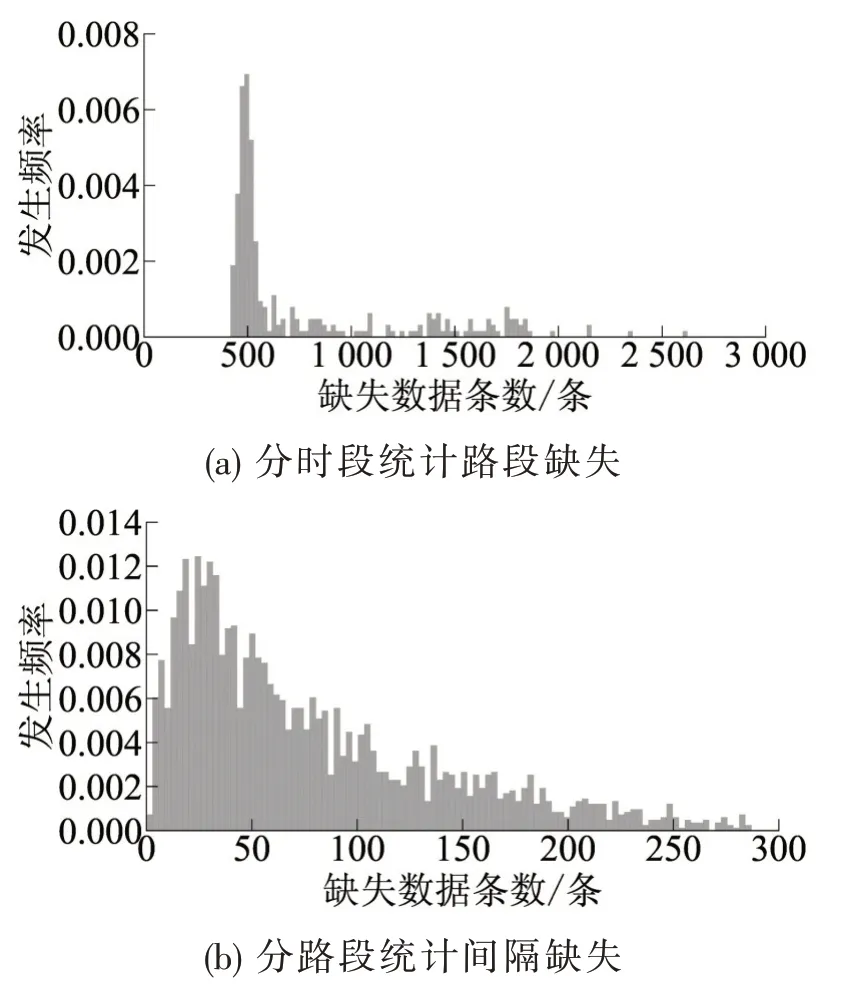
图1 数据缺失分组频率统计Fig.1 Frequency chart of different missing values for intervals and for links

记路段i长度为li，构造路段平均行程时间矩阵TA，矩阵第i行向量ti对应第i条路段在1 d 内各间隔的行程时间序列，其(i,j)元为第i条路段在第j个时间间隔期间的平均行程时间.对各路段做行程时间最大归一化，得到全日路段最大归一化行程时间矩阵，其(i,j)元

2 基于行程时间影响的关键路段识别

2.1 路径行程时间计算

路段是构成路网中所有出行路径的基本单元，出行者确定路径后，其行程时间等于从出发时间起计，经过路径中所有路段的行程时间之和.路段行程时间持续波动，故同一路径不同出发时间的行程时间不同，其计算步骤如下.

Step 1 确定出发时间，定位路径初始路段，初始化行程时间tl=0.

Step 2 在SA中标记各时间间隔所在路段编号，如图2所示.当前时间间隔剩余时长tC和当前所在路段的剩余行程距离sC关系有3种情况.

图2 路径行程时间计算示意图Fig.2 Schematic diagram of route travel time calculation

情况1tC期间完成sC行程后还剩余时间.将sC所用行程时间计入tl，更新tC为完成sC后剩余的时间.如后续还有其他路段，则继续分情况计算；否则，转至Step 3.

情况2tC期间不足以完成sC行程.将tC剩余时间计入tl，更新sC为当前路段未完成路段距离，转入下一个时间间隔继续分情况计算.

情况3tC期间刚好完成sC行程.将tC时间计入tl，如后续还有其他路段，则同时更新tC和sC为下一元素；否则，转至Step 3.

Step 3 保存tl为行程时间，结束计算.

2.2 路径池生成

将所有路段起、终节点(n=5 768 个)统一编号，构造当前路网的邻接矩阵P=(pij)n×n，其中，pij用非0 值和0 分别表示是否存在以节点i为起点、节点j为终点的直接连通路段，该非0值为连通路段长度.

构造路径集合Ll步骤如下.

Step 1 初始化参数.需生成路径数量Cl，路径长度最小值ll，单位为m，路径至少包括路段数量Cs.初始化路径实际长度la=0，路径实际包括路段数量Ca=0，初始化路段列表Ls.

Step 2 随机选取编号为q0的节点为起点.

Step 3 在P的第q0行向量中随机选择pij≠0 项，获取pij对应的路段编号，检查其是否已在Ls中.若是，则重新选择以避免路径闭环；否则，更新la=la+pij，Ca=Ca+1，在Ls中追加pij对应的路段编号，令q0=j.

Step 4 若la≥ll且Ca≥Cs，终止本轮计算，将Ls加入Ll；否则，返回Step 3.

Step 5 若 |Ll|=Cl，终止全部计算，返回Ll；否则，返回Step 2.

2.3 关键路段识别

生成路径池，以5 min为间隔计算池中各路径在全天不同时间出发所需行程时间，构成其行程时间序列；将该序列与经过各组成路段行程时间构成的序列对比，以皮尔逊系数为指标，选择该值高于设定阈值Pth的路段加入候选重点路段集合；综合所有路径计算结果，查找与池中Nth条以上路径行程时间高度相关的路段.

借鉴蒙特卡洛思想，将以上实验重复数次，综合筛选影响路网行程时间的关键路段集合.考虑路段平均长度552 m，为避免超长路径削弱短路径影响效应并兼顾每轮实验计算速度，特别控制路径长度且合理确定实验次数，确定参数ll=1 200 m，Cs=3，Cl=5 000，Pth=0.8，Nth=5.重复20 次实验并观测发现关键路段数量的变化，在第18 次实验后，关键路段数量保持533 条不再增加，如图3所示，其中5次实验的主要结果如表1所示.

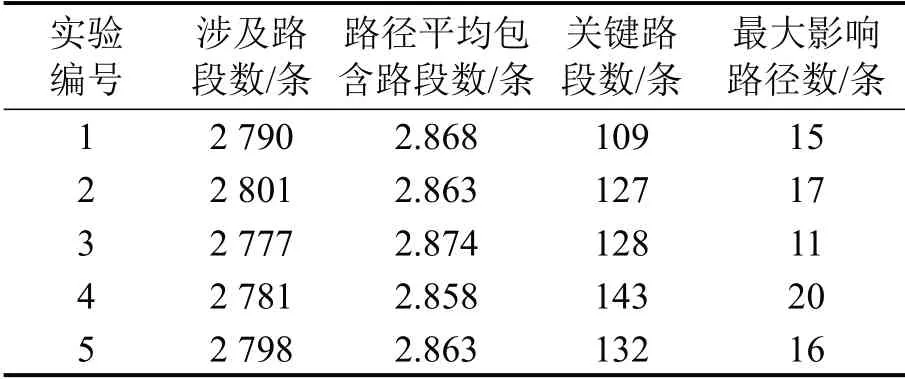
表1 关键路段查找实验部分结果Table 1 Part of results of critical-segment searching experiments

本方法由真实数据驱动，基于路段对行程的实际效用识别关键路段，无理想假设作为基础，识别结果可作为关键路段的“真值”.多次实验结果渐趋稳定说明方法可行，但其对算力有一定要求，且基于历史数据存在滞后效应.为实现主动管理，研究路段属性与其关键性的相关关系.以上述识别结果为依据，研究关键路段的主动查找模型，抽取路段属性作为建模基础.

3 路段属性及计算

3.1 基础属性

综合构造如下属性：

(1)路段长度属性(m).

(2)路段位置属性，分别标记内环以内(含内环)、中环与内环之间(含中环)、外环与中环之间(含外环)的路段属性为2、1、0.

(3)路段平均速度属性(km·h-1)，对SA各行求平均值得到.

(4)路段速度标准差属性(km·h-1)，对SA各行求标准差得到.

(5)路段道路等级属性，该属性与路段红线宽度、车道数量等相关，有一定代表性.分别标记快速路、主干道、次干道、支路路段属性为3、2、1、0.

3.2 行程时间曲线模糊聚类属性

路段行程时间序列波动较大，但整体波动水平和波动聚集存在特征.由Dunn[5]提出的模糊聚类算法(Fuzzy C-Means Clustering，FCM)引入隶属度概念以描述样本属于各个类别的概率，广泛用于交通分析.

图4 不同聚类数时Xie-Beni 指标值变化Fig.4 Value of Xie-Beni index corresponding to different clustering parameters

取K=3，绘制各类路段的最大归一化行程时间序列曲线及其聚类中心曲线如图5所示.不同聚类中心的数值水平有明显差异；全天趋势呈现类似规律，在第95和第220个时间间隔，即当日08:00前及18:30后出现行程时间高峰，但峰值高度有区别.

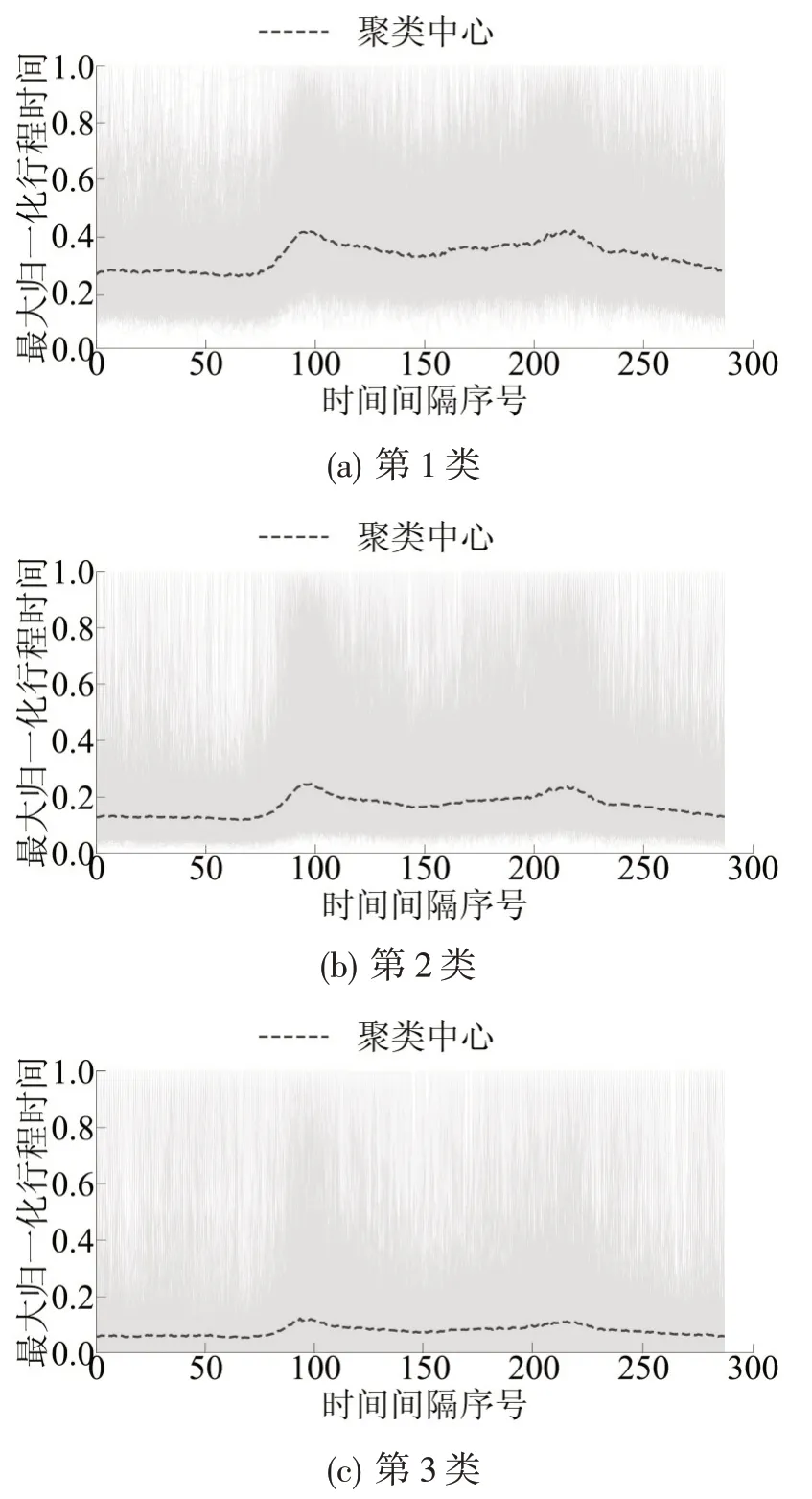
图5 不同聚类结果的最大归一化行程时间序列曲线及聚类中心曲线Fig.5 Maximum-normalized travel time series curves and clustering center curves of different clusters

预计路段曲线类型对路段是否为关键影响路段有指示意义，构造路段类型属性，分别标记图5中3类路段属性为0、1、2.

3.3 行程时间序列结构性变点相关属性

Inclan[6]在1994年提出的ICSS(Iterative Cumulative Sums of Squares)算法被广泛用于检测时间序列的结构性变点(简称变点)，李玮峰[7]证明其用于研究道路行程时间序列特征的可行性.

ICSS 分析要求目标序列为平稳序列，为此对每条路段行程时间序列进行对数差分处理为Di[7]，该序列中第j个元素dij为

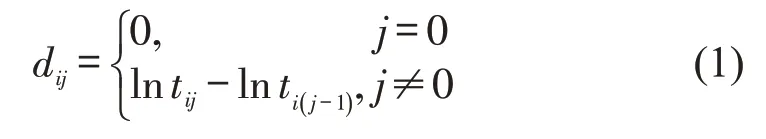
任取两条路段Di序列，如图6所示.对全部路段进行ADF 检验显示，其Di均为平稳序列，故可作为ICSS算法的输入.

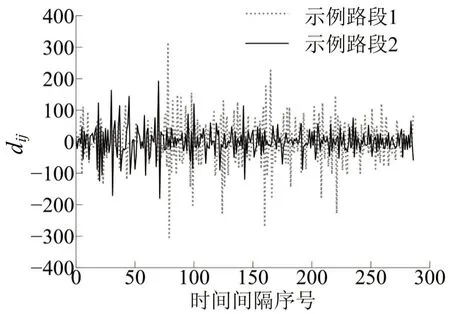
图6 两条路段的行程时间对数差分序列Fig.6 Logarithmic difference sequences of travel time for 2 segments

ICSS 运算结果显示，当日共有982 条路段存在变点，其变点数量区间对应的频率和变点所在时间间隔如图7所示，少数路段变点数明显多于其他路段.从路网整体看，变点出现有一定聚集性.随机选取15 条变点高发路段，标记其变点出现时间间隔、位置，如图8所示，可见单条路段也同样存在变点时间聚集性.

图7 变点数量频率统计及时间分布情况Fig.7 Frequency statistics and time distribution of change points

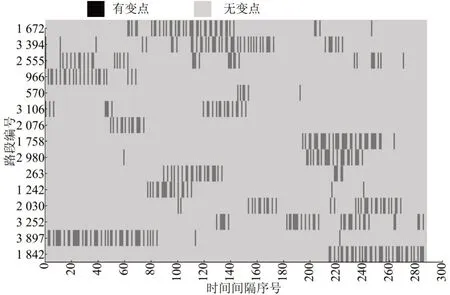
图8 15 条路段结构性变点出现时间间隔Fig.8 Intervals when structural change points emerged of 15 selected links

同时间窗口内变点数量越多的时间序列其方差变动越频繁，稳定性越差，对行程时间将产生更大影响.一个路段的行程时间对数差分序列变点个数可能与该路段行程时间波动特征相关，构造路段变点属性，记录对应路段当天的变点个数.

4 关键路段查找建模

4.1 建模过程及结果

综合7个属性，将路段类型属性以独热编码形式分解为3 个哑变量，再补充一个常数变量，扩展为10个变量.鉴于部分变量为类别变量，以kendall系数初步考察相关性，如图9所示.

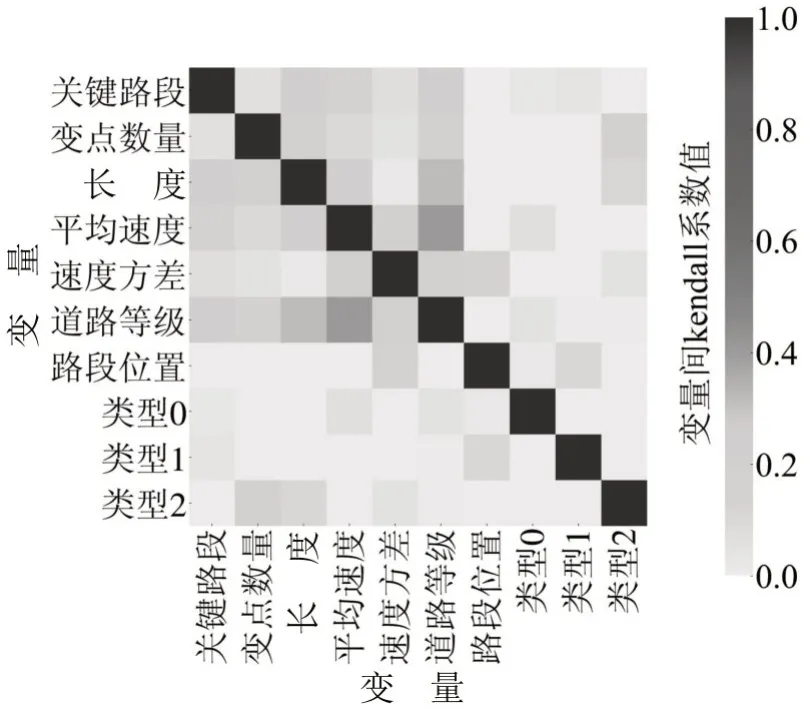
图9 变量相关系数热力图Fig.9 Heatmap of correlation coefficient of variables

变量间非强相关，除道路等级较高路段平均行程速度快这一常见规律外，还有以下结论：路段速度方差与道路等级和路段位置相关，等级越高、位置越靠近城市中心，则速度方差可能越大；路段变点数量与路段长度、道路等级相关.

聚类类型和路段属性有关联：类型0 路段的道路等级相对较高，类型1 路段位置更靠近城市中心，类型2 路段的变点数量、速度方差和长度数值更大.可见聚类结果可能包含路段特性的其他信息.

构造路段关键标记属性作为因变量，记533条关键路段该属性为1，其他路段为0.综合上述10个自变量构建二项Logit模型，称模型1.如表2所示，除变点数量和路段位置外，其余自变量均明显影响路段关键性.

4.2 模型评价与讨论

现仅保留3.1 节的基础指标构建二项Logit 模型作为对比模型，称模型2.结果显示，除路段位置标记外，其余自变量均影响路段关键性.

将数据代入两个模型，比较预测指标，如表3所示.

两个模型与随机分类器的ROC曲线对比如图10所示.可见其预测表现都高于随机分类器，但模型1 AUC指标明显优于模型2.

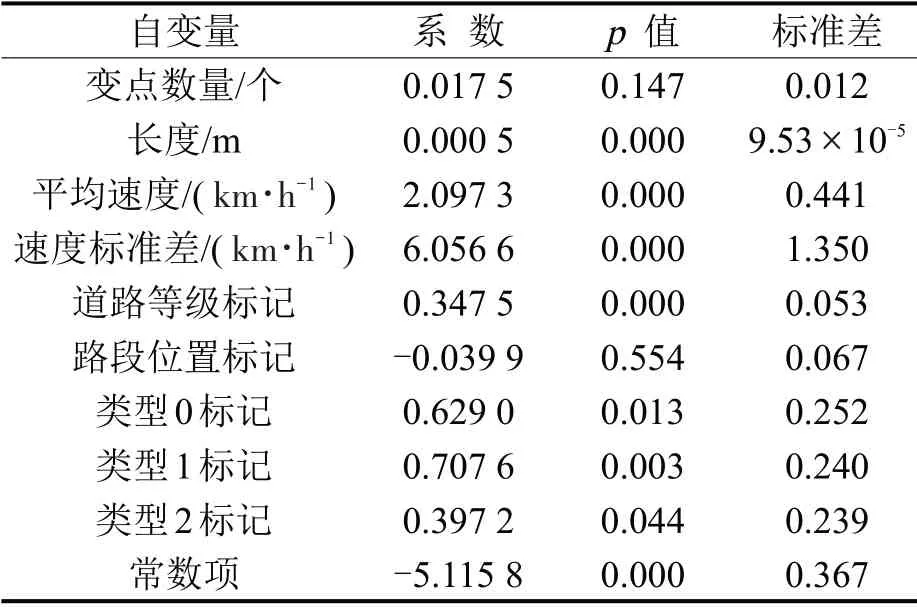
表2 Logit 模型1 计算结果Table 2 Results of Logit model NO.1

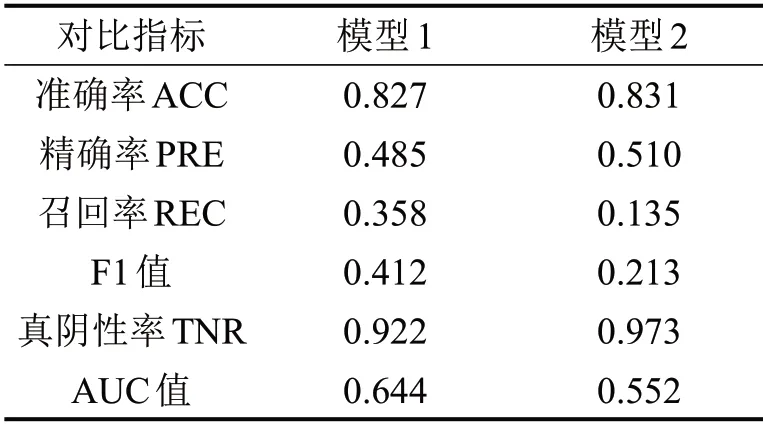
表3 模型指标对比Table 3 Comparisons of model indices

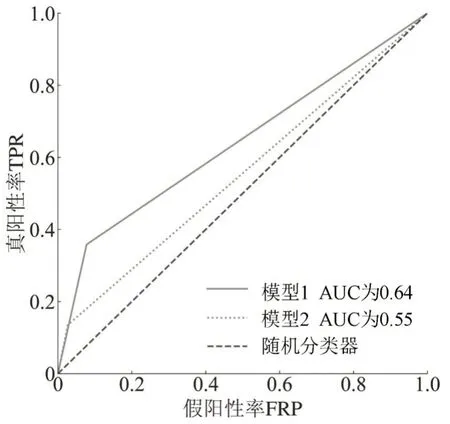
图10 模型与随机分类器ROC 曲线对比图Fig.10 ROC curve comparison among 2 models and random classifier

综上，基于路段长度、道路等级和行程速度统计参数等基础属性预测某条路段是否对路网行程时间有明显影响，ACC 较高，考虑到路网2 884 条路段中有81.5%的路段并非关键路段，样本有一定偏移，这个标准不难达到，实际上与市场份额模型相比，模型2的优势很小，其REC仅为13.5%，查找真正的关键路段能力很差，导致模型2 的F1 和AUC 指标较低.模型1 的ACC 和PRE 两项指标与模型2相差不大，REC和F1值更理想，查找真实的关键路段能力更好，可见基于最大归一化行程时间的聚类在模型中有一定效用.

虽然路段变点在时间分布上有明显的统计规律，且对不同路段有显著差别，但对模型1 的预测没有贡献，可见变点数量对行程时间波动的常发性与波动集中出现的时间有揭示作用，但不代表波动的程度，这也体现在图8中变点数量与标准差两个属性相关性不大，高频小幅度的路段行程时间波动可能不足以对路径行程时间造成影响.但变点数提供了观察路段行程时间稳定性的新维度，变点在不同路段上及路网整体出现的聚集特性可作为行程时间稳定性评价的参考因素之一.

5 结 论

基于蒙特卡洛思想随机构造路径并基于行程时间序列相关性识别重点路段，在多轮实验后呈稳定结果，证明方法可行.最大归一化行程时间、行程时间对数差分序列的变点数量可作为描述路段行程时间特征的两个新属性，前者可提升自动查找关键路段的二项Logit 模型性能；后者对模型没有贡献，但有别于量化行程时间波动程度的传统指标，提供了行程时间波动常发性和聚集性的新信息.