基于出行行为模型的出行感染风险评估——以新冠肺炎疫情期间江苏省地区为例

曹 奇，任 刚*，李大韦，朱茂莹，马景峰，宋建华，朱玉霖，何煜洪

(1.东南大学a.江苏省城市智能交通重点实验室，b.现代城市交通技术江苏高校协同创新中心，c.交通学院，南京211189；2.南京大学政府管理学院，南京210023)

0 引 言

交通防控是阻击疫情的必要手段[1-2].同时，交通系统也是疫情传播的重要途经[1].与以往国内外遭遇自然灾害或事故时采用“快速救援疏导”的交通应急策略不同[3]，我国政府果断选择交通禁行、限行等出行管制措施以阻断此次新型冠状病毒肺炎(COVID-19)疫情的传播.2020年1月23日，武汉全面进入“封城禁行”状态，暂停运营全市城市公交、地铁、轮渡、长途客运，并关闭机场、火车站离汉通道.随后，全国大部分地区根据病毒传播情况采取了不同程度的交通管制措施[4].在疫情快速传播阶段，这些措施有效阻断了疫情在国内的全面爆发[3].但需要注意的是，刚性出行(如就医、购买食物等)对维持居民基本生活具有不可替代的作用[4].施行无差异限行、禁行措施，不仅对居民的日常生活造成巨大损失，更无法保障抗疫前线工作人员(特别是医护人员)的通勤需求[1].因此，准确评价疫情期间不同出行行为的出行风险对完善交通应急管理策略具有重要意义.

风险即损失发生的可能性[5-6].在新冠肺炎疫情背景下，出行感染风险是指出行者进行出行活动时被病毒携带者传染的概率.新冠病毒只有当未感染出行者和病毒携带者存在于一定的空间距离和时间间隔范围内时，才可能通过飞沫、接触及气溶胶等方式传播[2,4,7].而这两类出行者在交通系统中的时空关联程度由其出行时间、方式及活动内容等行为共同决定.因此，建立出行行为模型是评估新冠肺炎疫情期间出行感染风险的必要条件.

构建基于出行行为的出行感染风险评估模型面临以下两个难点：

(1)缺乏针对重大突发公共卫生事件的出行风险评估方法.当前交通领域提出的出行风险评估方法主要聚焦于交通事故方面.该类方法基于人—车—路三方面的风险要素构建出行风险概率模型，并不适用于疫情期间的出行感染风险评价.

(2)缺乏针对出行者全时域连续出行行为的建模手段.病毒的传播可能发生在出行链的任何环节，因而需要对出行时间、出行活动内容及出行方式等出行行为在24 h 全时域上建模分析.当前出行行为分析模型多以离散出行为研究对象，无法准确、全面评估疫情期间出行风险.

针对以上问题，本文分别构建病毒携带者和普通出行者疫情期间的全出行链行为分析模型，应用贝叶斯公式建立感染风险概率与出行行为的关联联系，实现对疫情期间居民出行感染风险的全面评估.

1 出行感染风险模型

疫情期间，出行感染风险是指出行者通过m方式在t时刻参加活动a接触到病毒携带者并感染的风险概率，记为P(D=1|m,t,a).其中，D=1 为出行者被新冠病毒感染，(m,t,a)为其选择的出行方案.根据贝叶斯公式，P(D=1|m,t,a)可以被分解为

式中：P(m,t,a|D=1)为病毒携带者选择出行方案(m,t,a)的概率，表示其通过m方式在t时刻参加活动a的概率；P(m,t,a|D=0)为普通出行者选择出行方案(m,t,a)的概率；P(D=1)和P(D=0)分别为发生感染和不发生感染的先验概率.

发生感染的先验概率由传染源数量和总人口数量之比决定，即

式中：N+为尚未采取隔离措施的病毒携带者人数，即传染源数量；N为城市总人口数.

不发生感染的先验概率P(D=0)为

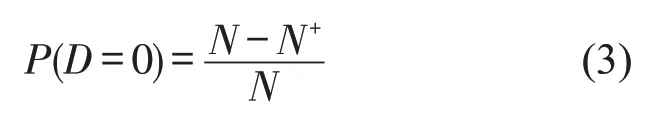
Li等[2]指出疫情初期新冠肺炎的平均潜伏期为5.2 d.这意味着病毒携带者在出现症状前拥有平均5 d 的自由出行史.因此，可向后取5 d 的新增病人确诊数之和作为当日交通系统中尚未采取隔离措施的病毒携带者数量N+.具体取值如表1所示.

2 出行行为模型

2.1 模型定义

普通出行者和病毒携带者的出行行为模型可根据其各自收集的调查数据分别训练得到.如图1所示，出行链由活动节点(Sojourn Nodes)和出行连接(Trip Links)组成.定义Ai为出行链的活动链{a1,…,an,…,aN}，其中，an为出行者参与的活动，包括就医、工作、差旅、购物、娱乐、居家6类.

将参与各项活动的出行方案按时间顺序排列，得到出行链的出行连接序列.本文将该出行连接序列{l1,…,ln,…,lN}定义为出行路径，用Pj表示，其中，ln表示两个相邻活动an和an+1的出行连接方案，包括出行模式mn和到达时刻tn(活动开始时刻)两项内容，即ln=(mn,tn).出行方式mn包括公共交通、私家车、网约/出租车、非机动车、步行5类；到达时刻tn按小时取整，即tn∈[0,1,…,23].

图2以A：{a1=居家,a2=工作,a3=购物,a4=居家}为例，基于时空坐标系描述了其可能的出行路径候选集.图2中的节点代表出行者参与的活动an，连接节点的线段代表出行连接方案ln=(mn,tn).将多个出行连接方案按时序排列便构成了该出行链的一个可行的出行路径Pj：{l1,…,ln,…,lN}.因此，活动链表达了出行者对参加各类活动的选择偏好，而出行路径表达了出行者对出行方式和到达时间的选择偏好.对出行者在全时域上连续出行行为进行建模就是建立出行者在活动链与出行路径两个层次上的行为选择模型.

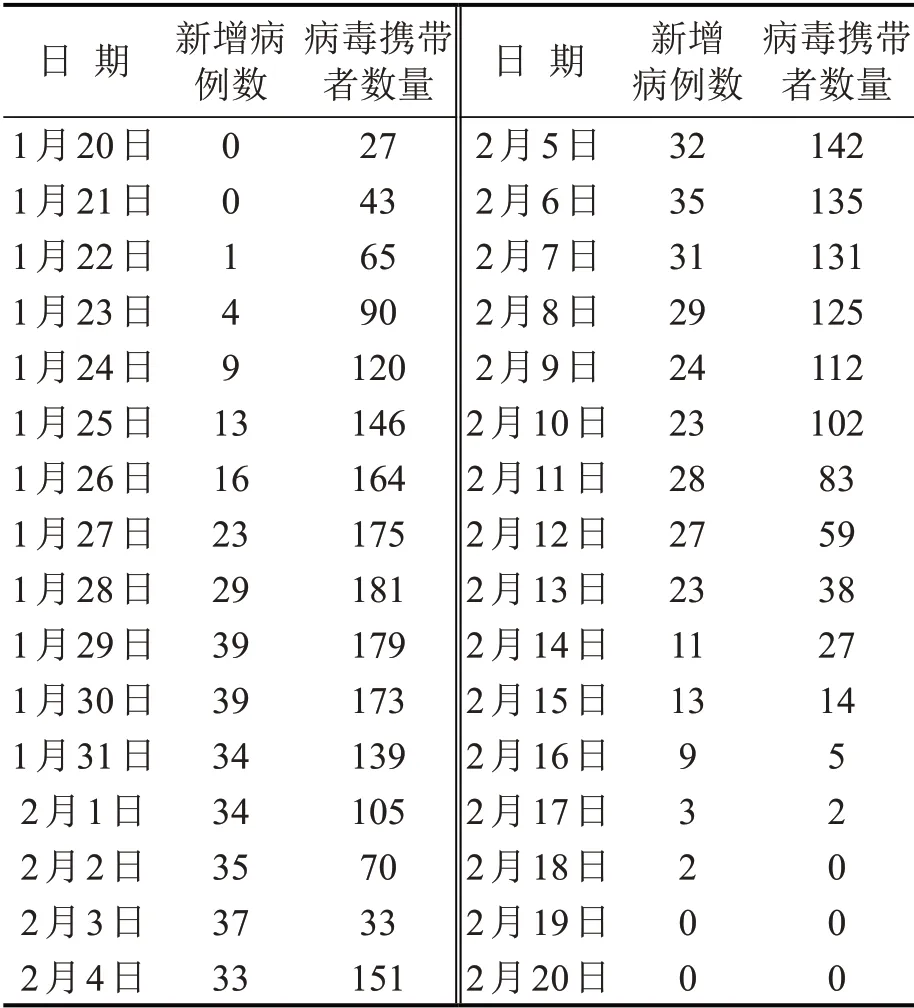
表1 江苏省疫情期间每天新增病例与未隔离病毒携带者估计数量Table 1 Number of new cases and non-isolated virus carriers per day in Jiangsu Province

图1 出行链网络与典型活动链Fig.1 Trip chain network and activity chain

本文使用Nested Logit 模型对出行者在活动链和出行路径两个层次上的选择行为进行建模[8-9]，即

式中：θ1和θ2为反应不同出行者出行偏好的系数；Ω为出行者24 h时域上可选择的活动链Ai的候选集合；Ψ为出行路径Pj的候选集合；Ui为活动链Ai的总期待效用，定义[10]为

式中：Uij为以出行路径Pj完成活动链Ai的净效用，可以由活动链的正效用与出行路径的负效用之和定义，即

图2 可行出行路径Fig.2 Alternative path

2.2 活动效用

候选活动链Ai效用主要由其包含的各项活动效用之和确定，即

式中：Ui,an为出行者从参与活动an中获得的效用，主要与活动开始时间和持续时间有关.出行者在时刻ti,an参加活动an持续时间长度τi,an获得的效用可以表示为活动an边际效应函数的积分形式[2,11-12]，即

式中；MUan(x)为活动an的边际效应函数.Li 等[10]提出可由一个钟形函数对全时域上(24 h)的活动边际效用变化进行模拟，其一般形式为

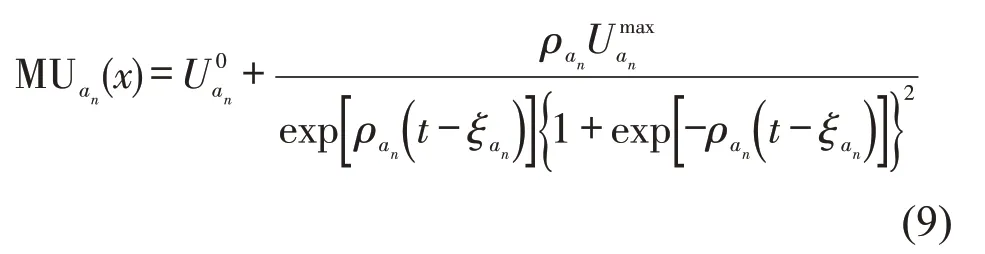
式中：为活动an的基准效用水平；为活动an的最大效用；ξan为决定活动边际效用达到最大的时刻，即拐点位置；ρan为决定活动边际效用曲线的斜率，即曲线的陡峭程度.普通出行者和病毒携带者不同活动的边际效用参数ρan可根据两类人群的各类活动的调查数据分别进行估计得到.

2.3 出行效用

由于疫情期间对确诊患者出行调查较为困难，假设候选出行路径的效用函数仅与年龄、时间、费用和延误4个特性变量成线性关系，即

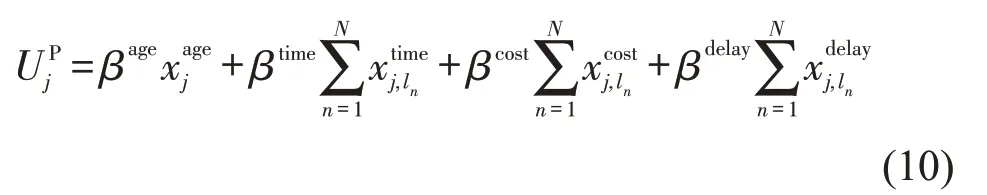
式中：为年龄特性变量的输入值；分别为参加活动an时所选择出行方案ln=(mn,tn)(使用mn出行方式在tn时刻到达活动地点)的出行时间、出行费用、出行延误；βage，βtime，βcost，βdelay分别为普通出行者和病毒携带者的出行偏好参数，可根据两类人群的出行调查数据分别进行参数估计得到.

式(10)中出行延误指早到或晚到活动地点的时间成本.参考Li等[10]研究，定义为

式中：为出行者期待的到达时刻；是到达时间可接受的范围.由于难以通过调查数据获取，本文假设是以tj,ln为中心的正态分布，即，其中，标准差δln主要由选择的出行方式决定.公共交通、私家车、网约/出租车、非机动车、步行5 类出行方式的δln值，据经验分别取8，10，12，3，2 min.就医、工作、差旅、购物、娱乐、居家6类活动的可接受的延误时间εan分别取10，0，0，10，10，10 min.

2.4 出行方案选择概率

对两类出行者在全时域上连续出行行为进行建模的目的是估计病毒感染者和普通居民的出行方案选择概率，从而根据式(1)计算居民出行感染风险.两类出行者的出行方案选择概率为

P(Ai,Mj|D=1)和P(Ai,Mj|D=0)由式(4)定义，可以通过收集病毒感染者和普通居民的出行行为数据分别对模型训练而得到.

3 案例应用与分析

3.1 数据收集

数据获取与收集始终是行为分析模型应用所面临的一个挑战[13].特别是新冠病毒携带者出行信息的收集，因巨大的感染风险而不可能通过常规交通调查获取.本文基于确诊病例的流行病学调查报告提取新冠病毒携带者的出行行为数据.以扬州市2020年2月9日的1 例新增确诊患者信息为例，如图3所示，其通报内容不仅包含了确诊患者个人属性信息，还通过文字描述了确诊患者出行历史信息.图3绘制了该病例1月17日的出行时空轨迹图，准确描述了其当日的活动内容，活动时间、出行方式等信息.以江苏省为研究对象，共收集151位新冠肺炎确诊患者的流行病学调查报告.

图3 流行病学调查报告样例Fig.3 An example epidemiological investigation report

为建立普通出行者的出行行为模型，通过线上问卷调查收集146 份普通居民疫情期间的出行历史数据.调查内容包括出行者个人属性信息和出行历史信息.表2总结了两个样本集的社会人口特征.

表2 样本数据社会人口特征Table 2 Social and demographic characteristics of sample dataset

3.2 参数标定

采用分阶段法[9]进行参数标定，并选取参数估计检验显著性水平为α=0.05.表3为出行效用参数的标定结果.拟合优度比值较高，说明模型具有较好的拟合.所有估计参数的t值均满足95%的置信度检验.出行路径的选择概率与出行时间和费用成负相关，符合现实规律.其中，普通出行者相较病毒携带者对出行时间和出行费用更为敏感，但具体原因还有待结合更大规模的样本数据进一步论证分析.

表4给出了活动效用参数的标定结果.病毒携带者和普通出行者出行行为的区别主要体现在就医和差旅两项出行活动上.图4比较了病毒携带者和普通出行者参加这两项活动的边际效用函数.

表3 出行效用参数估计结果Table 3 Estimated parameters of travel utility

表4 活动效用参数估计结果Table 4 Estimated parameters of activity utility

由图4可以发现

(1)病毒携带者就医出行的效用值远高于普通居民，说明病毒携带者具有较高的就医出行需求.这是因为每位确诊样本都有1次以上的就医出行历史.

(2)病毒携带者的差旅出行需求相对普通居民较高.可以推测差旅活动是输入型病例感染新冠病毒的重要原因.

3.3 出行风险评估

3.3.1 各类活动的出行风险

图5比较了疫情期间各类出行活动的出行风险，可得出如下结论：

(1)就医活动的感染风险先增后降，但始终维持在较高水平.这是因为医院是新冠患者出现概率较高的地方，所以就医过程中发生交叉感染的风险较高.

(2)疫情传播初期，差旅活动感染风险较高，但在1月25日后(农历春节后)迅速下降.可以推测春运期间的大规模人员流动推动了疫情扩大，而春节后的交通管控措施有效阻断了疫情传播.

3.3.2 各类出行方式的出行风险

疫情期间江苏省居民各类出行方式感染新冠肺炎的风险如图6所示.可得到如下结论：

(1)管理部门采取严厉的交通管制措施后，各类出行方式的出行感染风险经历了断崖式下降，极大降低了新冠肺炎病毒通过交通系统传播的风险概率.

(2)非机动车出行作为一种个体化程度最高的出行方式，在保持较低水平出行风险同时保证了一定的出行效率(特别是电动自行车).

图4 病毒携带者和普通出行者活动效用函数对比Fig.4 Comparison of marginal activity utility functions

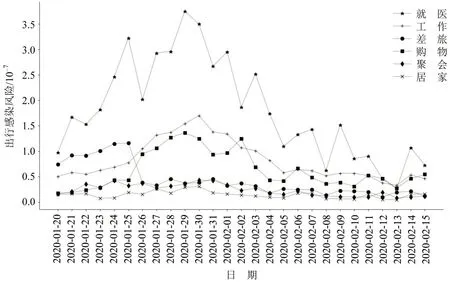
图5 不同出行活动的出行风险对比Fig.5 Travel risks for different activities

4 结 论

通过收集病毒携带者和普通出行者出行历史数据，比较分析病毒携带者和普通出行者的出行行为特征，揭示出行风险变化的内在规律.分析结论对制定重大突发公共卫生事件下交通运输应急管理策略具有启示意义：

(1)交通管控措施可有效降低各类出行活动和出行方式的出行感染风险.

(2)差旅活动具有较高的出行感染风险.交通管理部门应主动与卫生部门进行信息沟通，加强交通预警，提醒出行者减少出差等非生活必需出行.

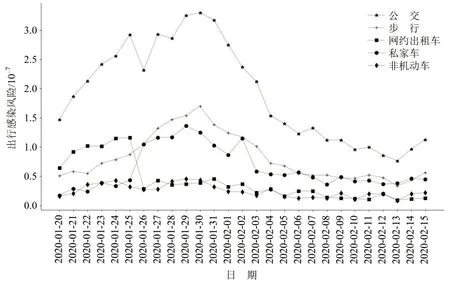
图6 不同出行方式的出行风险对比Fig.6 Travel risks for different modes

(3)就医出行在疫情传播的各个阶段都有非常高的出行风险.因此，应开通专门的发热病人分诊通道，避免在就医过程中发生交叉感染.

(4)非机动车特别是电动自行车作为一种载员密度较低，出行环境开放的出行方式，具有较低的出行感染风险，还能兼顾一定的出行效率.政府应加大电动自行车的供给能力，以满足居民的刚性出行需求(特别是医护工作者)的通勤需求.