基于BPNN的COVID -19疫情预测及SEIR的高校复学分析

周彩霞, 张涛, 滕懿振, 刘加荣

2019冠状病毒疾病(coronavirus disease 2019，COVID -19)是由严重急性呼吸综合征冠状病毒2型(severe acute respiratory syndrome coronavirus 2，SARS-CoV-2)引起的。该病毒是一类β-冠状病毒，有许多潜在的自然宿主、中间宿主和最终宿主，由于其具有较高的传染性和传播力，迅速导致了全球大流行，对公共卫生系统构成严重威胁[1-3]。为了遏制病毒的传播，我国积极开展COVID -19疫情防控工作，包括大规模隔离、社会隔离、社区遏制和交通限制[4]。此外，政府不断加大对COVID -19患者医疗资源的投入[5]。目前我国的疫情形势已得到较好的控制，但无症状感染者具有病毒传播能力，且临床症状隐匿而无法有效识别，这容易形成防控措施的漏洞[6-9]。截至2020年7月14日24时，据31个省(自治区、直辖市)和新疆生产建设兵团报告，累计追踪到密切接触者767 432人，尚在医学观察的密切接触者3 577人[10]。虽然，目前国内疫情已基本稳定，但密切接触者可能会造成无症状感染者数量的上升，从而影响高校复学。学生数量较大的高校何时复学，以及采取何种管控措施，降低在校感染的风险，成为目前社会关注的重点。因此本研究通过建立数学模型，对世界主要国家的疫情发展趋势进行预测，并对中国高校复学时间及方式进行分析。

1 资料与方法

1.1 数据来源

根据国家卫生健康委员会官网公开的疫情相关数据，统计2020年1月22日—7月14日的中国内地累计确诊人数、累计死亡人数、累计治愈人数、累计密切接触者数量、累计无症状感染者数量以及美国、意大利累计确诊人数，基于深度学习进行建模。

1.2 模型构建和数据分析

1.2.1 BP神经网络预测模型本文通过Matlab软件，构建了三层BP神经网络(BPNN)：输入层(x)，隐藏层(h)，输出层(y)。如图1所示，该模型可依据疫情更新数据进行自我学习，调整内部的权重参数，具有较好的识别、训练和容错能力。定义的输入和输出节点数均为1个，时间作为输入节点，确诊人数作为输出节点。通过经验公式设定隐含层节点数量为5个，目标误差设置在0.000 5，经过多次拟合，选取学习效率为0.35，模型的预测精度较高。利用BP神经网络在复杂系统评价中具有的评价精度较高的优点，考虑了三个分别采取了不同程度隔离措施的国家疫情数据样本，根据数据拟合结果评价，中国隔离措施为严格，意大利隔离措施为一般严格，美国隔离措施为不严格。在此次建模过程中分别对2020年1月22日—2020年7月14日三个国家的疫情确诊数据进行训练并预测了三个国家未来180天的疫情数据。鉴于数据样本过小，本文训练数据和测试数据保持一致，均为全部数据集，以此来验证模型的预测精度。

1.2.2 SEIR模型SEIR模型适用于具有一定潜伏期的传染性疾病，是传染病预测最为常用的模型之一。在SEIR模型中(见图2)，人群被定义为四部分：第一部分为易感者(susceptible)，表示人群中易于被病毒感染的人数，用S表示；第二部分为潜伏者(exposed)，表示人群中感染未出现症状人数，用E表示；第三部分为感染者(infectives)，表示人群中患病的人数，用I表示；第四部分为恢复人群(recovered)，表示患病后恢复的人数，用R表示；即N=S+E+I+R。P为感染系数1，代表易感人群与感染者接触后被感染的概率。Pa为感染系数2，代表易感人群与潜伏者接触被感染的概率，τ代表潜伏者转化为感染者的概率，γ代表恢复概率。本文对各种传染指标进行了数据拟合，考虑了在采取不同管控措施及不同复学规模下，与感染者和潜伏者接触的易感人群数量的变化，通过SEIR模型迭代未来300天的数据来分析潜伏者和感染者数量是否会存在二次高峰，以此来评价不同复学时间及复学方式的可行性。

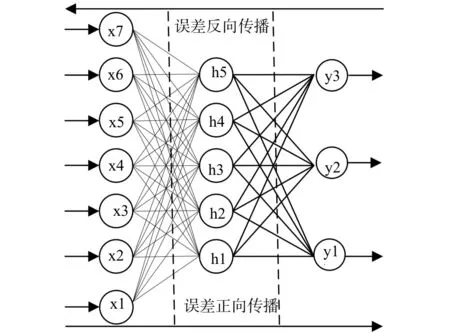
图1 BP神经网络结构原理图

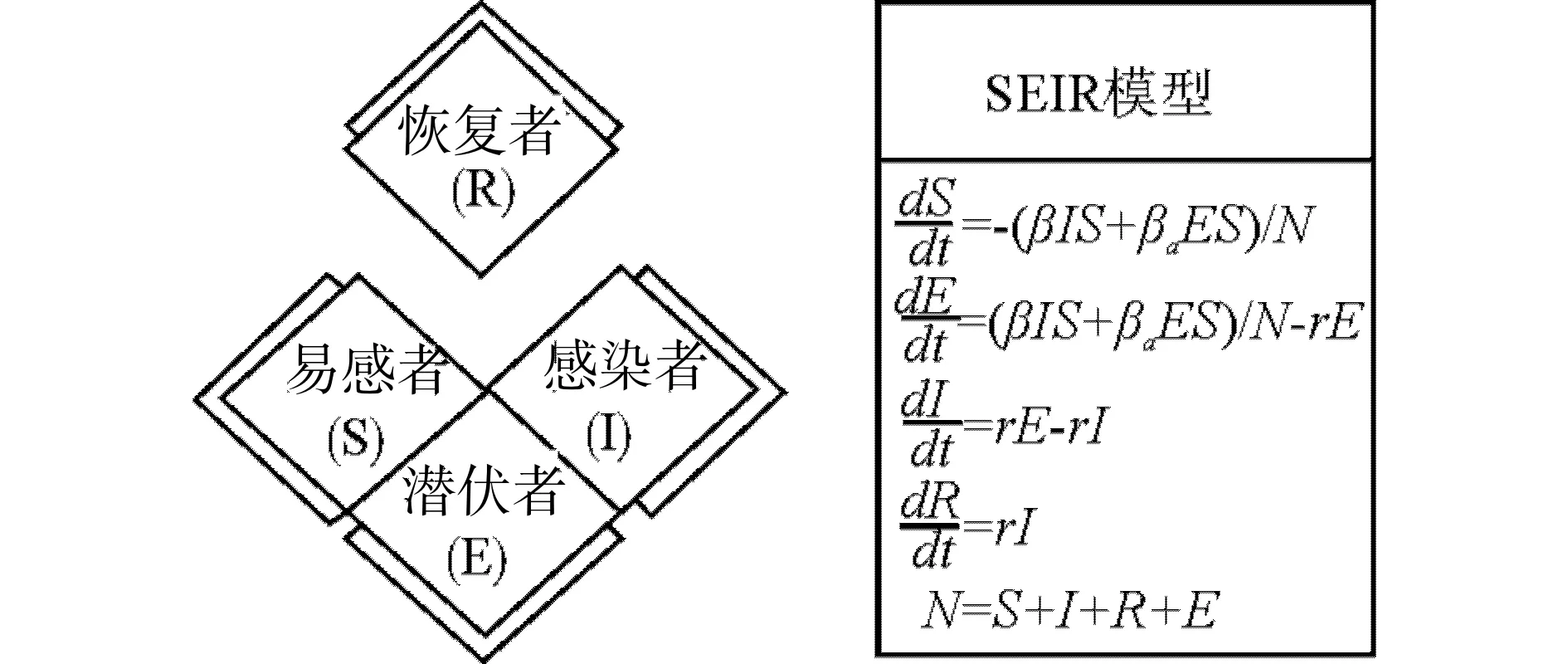
图2 SEIR模型

1.3 统计分析

本研究利用MatlabR 2018、Python 3.7.0仿真平台进行分析。

2 结果

2.1 基于BP神经网络的中国、美国和意大利在未来半年确诊病例数预测

本研究统计了2020年1月22日-7月14日中国、意大利和美国官方报道的累计确诊病例数。如图3(A-C)所示，每个国家包含175个数据，训练数据和测试数据保持一致，均为全部数据集，以此来验证模型的预测精度。并进行了模型预测的相对误差分析(见图3 D-F)，在模型训练后期，相对误差基本趋于0。结果表明，利用BP神经网络预测的COVID -19确诊人数与前期已知阶段的实际确诊人数基本相符。该模型可以对中国、美国和意大利的疫情发展趋势进行合理预测。因此，本研究对以上三个国家未来半年(180天)累计确诊病例数进行了预测。目前，中国疫情形势已趋于稳定，将在9月中旬达到峰值，累计确诊人数预测值约为87 231(见图 3 G)；意大利将在11月初达到峰值，累计确诊人数预测值约为294 083(见图3 H)；美国在不加强防控的情况下，峰值的出现将不早于明年1月中旬，累计确诊人数预测值约为6 549 553(见图3 I)。

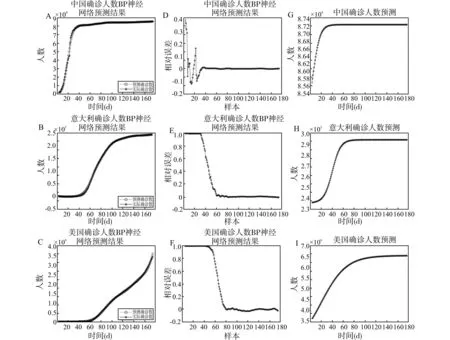
注：A为中国疫情数据训练预测对比；B为意大利疫情数据训练预测对比；C为美国疫情数据训练预测对比；D为中国疫情数据训练样本误差；E为意大利疫情数据训练样本误差；F为美国疫情数据训练样本误差；G为中国未来180天疫情预测结果；H为意大利未来180天疫情预测结果；I为美国未来180天疫情预测结果图3 BP神经网络模型验证及各国疫情预测结果

2.2 基于SEIR模型的高校复学情况下疫情发展趋势的预测

根据拟合的各参数值，利用SEIR模型分析高校复学情况下COVID -19疫情的发展趋势。假设某高校总人数(易感者)为10万，从2020年1月23日起居家隔离，均有采取严格的管控措施，易感者数量会显著降低；潜伏者与感染者数量会在达到峰值后降低，并逐渐趋近为零；康复者数量上升并趋于稳定。见图4。

若在疫情发生120天后(即4月底)采取部分分批复学的形式，疫情基本不会因学生在校产生二次暴发。潜伏者与感染者数量会在疫情发生160天后清零。若188天后(两个医学观察期)在无外来病例输入的情况下，基本不会出现在校感染。见图4 A。

若在疫情发生120天后采取严格管控下的全面复学，疫情在学校出现二次暴发的可能性很小。但潜伏者与感染者数量清零可能会推迟到疫情发生的220天后。若248天后(两个医学观察期)在无外来病例输入的情况下，基本也不会出现在校感染。见图4 B。

若在疫情发生120天后采取无严格管控下的全面复学，疫情可能在学校出现二次暴发。同时潜伏者与感染者数量清零可能会推迟到疫情发生的240天后，若268天后(两个医学观察期)在无外来病例输入的情况下，在校感染可能性较低。见图4 C。

3 讨论

与SARS和MERS相比，虽然COVID -19的死亡率较低，但其传染性明显更强[11]。自日本钻石公主号发现大量COVID -19感染者以来，世界各国相继出现确诊病例，疫情形势日趋严重，这对各国卫生系统和经济等造成了重创。自COVID -19疫情暴发以来，国内外多项研究提出传染病动力学模型，依托疫情相关数据，科学预测疫情发展趋势，为公共卫生管理者的决策与高效干预措施的实施提供了重要依据[11-16]。范如国等[13]建立了SEIR传染病动力模型，对三种不同潜伏期下的武汉疫情拐点和COVID -19确诊病例数的峰值进行了预测；魏凤英等[14]利用SEIR模型对全球主要疫情国家的总体态势进行了研判，并针对复工复产对疫情发展可能产生的影响进行了数值模拟；Tomar等[11]利用Long-short term memory(LSTM)模型和曲线拟合，评估了印度未来30天COVID -19确诊病例数，并检验了隔离措施的有效性；Chimmula等[15]利用LSTM模型预测加拿大COVID -19传播的时间序列，并比较了加拿大、意大利和美国的传播率；也有研究采用基于循环神经网络的LSTM模型预测SARS-CoV-2未来的突变率[16]。但这些研究大都立足于疫情早期的数据，着重于疫情峰值、拐点、传播率和防控措施有效性等问题，未在此基础上进一步考虑疫情趋于稳定后的具体复学方案。本研究利用最新的疫情数据建立了BP神经网络模型，分析三个采用不同程度隔离措施的国家(中国、意大利和美国)的疫情形势，并预测其未来半年累计确诊病例数。中国疫情形势已趋于稳定，不会出现“二次高峰”。意大利采取了全国停课、封锁交通等防控措施，累计确诊人数预计在11月初达到峰值。而美国虽然疫情出现较晚，但防控措施不够严格，预测累计确诊人数峰值不会早于2021年1月中旬。对比分析三个国家的疫情发展趋势，可以看出中国疫情防控取得了重大战略成果。在此基础上企事业单位也精准有序复工复产。因此现阶段国内更关心的问题在于高校复学、大型体育赛事、演唱会和商业集会的重启。虽然某些高校已采取部分、分批的复学形式，但鉴于高校学生数量大，管控措施的实施可能存在诸多困难，还应考虑复学是否会造成疫情“二次高峰”。因此，本研究依托国内最新疫情数据建立了SEIR模型，分析高校复学时间及复学规模对高校疫情的影响。结果显示，在疫情发生后188天左右(7月上旬)，高校可以采取严格管控的部分复学，这与部分高校和教育部政策基本相符。在疫情发生后248天左右(9月上旬)，高校可以采取严格管控的全面复学。从理论上分析，在疫情发生后268天左右(9月底)，高校可以采取无严格管控的全面复学。但鉴于预测结果显示，在疫情发生120天后采取无严格管控的全面复学将出现疫情二次暴发、潜伏者及感染者数量上升。因此，不能排除在9月底采取无严格管控的全面复学后潜伏者及感染者数量上升的可能性。

注：A为采取措施的部分复学；B为采取措施的全面复学；C为未采取措施的全面复学图4 基于SEIR模型的高校复学分析

本文采取的BP神经网络具有较强的非线性映射能力、自学习能力、泛化能力、容错能力。这些优点使其广泛应用于传染病疫情预测、疾病的临床诊断与治疗分析等方面。但是随着应用范围的逐步扩大，BP神经网络也暴露出了一些不足，主要是存在局部极小化问题和样本依赖性问题[17-18]。SEIR模型加入了人口流动和潜伏者两个影响因素，相较于SIR考虑更为全面，能够较好地对病毒潜伏者乃至整个疫情的趋势进行预测。但SEIR模型对人群的分类还不够细致，对数据的初值较为敏感，可能会对结果的稳健性产生很大影响[12，19]。此外，BP神经网络和SEIR模型更好的有机性融合也将是下一步研究的重点。

综上所述，该模型预测的结果与疫情实际发展趋势和相关部门出台的政策基本吻合，可为高校下一步复学计划提供理论参考，同时可进一步推广至大型体育赛事、演唱会、商业集会等重启时间的分析，刺激消费，推动经济复苏。