基于改进VMD的离心泵空化声发射信号特征提取

刘忠，张许阳，邹淑云，李志鹏

(长沙理工大学能源与动力工程学院，湖南 长沙 410114)

空化会降低离心泵的工作效率，并诱发振动、压力脉冲和噪声等，严重影响泵的安全运行和使用寿命[1].国内外学者根据空化引起的相关信号变化，采用振动、压力脉动、噪声等检测手段开展研究[2].声发射(acoustic emission，AE)技术作为一种先进的检测手段，对检测对象的运行无干扰，能有效避开低频信号的干扰，因此也被用于离心泵空化状态检测.ALFAYEZ等[3]利用AE技术对离心泵空化进行检测，研究了AE信号电压等级、均方根等特征参数与汽蚀余量之间的关系.刘忠等[4]采用小波方法提取离心泵空化AE信号的能量特征及其分布频段，为空化状态的判别提供依据.但小波方法易受到小波基和分解层数的影响，无法实现非线性、非周期信号的自适应分解[5].LI等[6]采用改进的经验模态分解(empirical mode decomposition，EMD)方法，自适应地分解离心泵空化信号，采用若干本征模态识别离心泵空化发展程度.但EMD方法缺乏坚实的理论基础，且存在模态混叠、端点效应等问题.

变分模态分解(variational mode decomposition，VMD)[7]是一种新型非递归自适应的信号处理方法，具有精度高、噪声鲁棒性强的特点，避免了传统EMD方法因循环递归分解而产生模态混叠的缺陷，受到广泛的关注和研究.然而，目前鲜见VMD用于离心泵空化AE信号特征提取的文献.同时，VMD算法需要根据经验人为预先确定分解层数和惩罚因子，直接影响信号自适应分解效果.信息差异系数反映了信号之间的差异程度：差异系数越大，信号之间的区别度越大.包络熵的大小反映了信号的稀疏特性，可将包络熵极小值作为VMD参数优化的目标函数[8].受此启发，文中提出区分信号之间差别度的包络熵差异系数，用于确定VMD算法中的分解层数.同时，人工蜂群算法(artificial bee colony，ABC)[9]与蚁群算法、遗传算法、粒子群算法等相比，具有操作简单、参数设置少、搜索精度较高等优点，用于参数优化取得了较好的效果[10].该算法可用于VMD算法中的惩罚因子寻优.因此，文中基于包络熵差异系数和ABC算法，提出一种改进VMD算法，并将其应用于离心泵空化AE信号特征提取.

1 基本原理

1.1 VMD算法

VMD算法的实现主要分为构造变分问题和求解变分模型2步.

1.1.1 构造变分问题

VMD是将输入信号f(t)分解为k个具有特定稀疏性的相互独立的本征模态函数(intrinsic mode function，IMF).受约束的变分问题可描述为

(1)

式中：h为模态分量的单边频谱；uk,ωk分别为IMF具有有限带宽的模态分量和中心频率;f(t)为输入信号.

1.1.2 求解变分模型

1) 通过引入惩罚因子α和拉格朗日乘法算子λ(t)，将约束性变分问题变为非约束性变分问题.增广拉格朗日表达式为

(2)

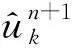
(3)

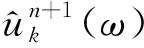
(4)

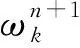
采用式(5)更新λn+1，即

(5)

在VMD的分解过程中，若分解层数k取值过大，则会造成过分解，出现虚假模态；反之，会导致分解不充分，产生模态混叠.同时，若惩罚因子α取值过大，则会造成分解的模态函数频带过窄，丢失有用信息；反之，会造成频带过宽，携带干扰信息.经深入研究发现，通过先优化k再优化α，可改进VMD算法.

1.2 包络熵差异系数

在VMD分解过程中，会得到k个IMF分量的包络熵值，分别记作E1，E2，…，Ek，代表该分量所携带信息量的大小.包络熵差异系数C可定义为

(6)

式中：Eav为k个IMF包络熵的平均值；N为每层信号的个数；a(j)是第i个IMF分量IMFij经Hilbert解调后得到的包络信号；pj是a(j)的归一化形式.C值越大，说明IMF之间的差异越明显，VMD的分解效果越好.

1.3 ABC算法

ABC算法是一种通过模拟蜜蜂采蜜行为解决数值优化问题的算法.将蜜源i(i=1, 2, 3, …,S)抽象为一系列空间点，作为寻优结果的潜在解.初始蜜源满足

xid=xmin,d+rand[0,1](xmax,d-xmin,d) ，

(7)

式中：xid为第i个蜜源xi的第d维的值，其中i为蜜源，d为[1，D]中的1个随机整数，表示雇佣蜂随机地选择1维进行搜索，D为参数个数；xmin,d，xmax,d分别为第d维蜜源的最小值和最大值.待寻找的新蜜源满足

vid=xid+φ(xid-xjd)，

(8)

式中：xjd为邻域蜜源，j∈{1，2，…，S}，j≠i；vid为新蜜源位置；φ是服从[-1，1]均匀分布的随机数，决定扰动幅度.利用式(8)随机寻找新蜜源，根据选择概率Pi的大小判断是否产生新蜜源.

(9)

式中：fi为用于判断蜜源质量的适应度.

2 改进VMD算法

采用包络熵差异系数和ABC算法，分别对分解层数k和惩罚因子α这2个参数进行寻优，从而实现对VMD算法的改进.

包络熵差异系数C在不同分解层数k下的取值也不同.C值越大，说明VMD的分解结果差异度越大，分解效果也越好.VMD算法的k值优化步骤如下：① 预设VMD初始α值，设定k的取值范围；② 计算不同k值对应的C值；③ 将最大C值对应的k值确定为最优分解层数kopt.

待kopt确定后，将惩罚因子α值作为ABC算法的初始化蜜源值、包络熵差异系数C值作为ABC算法的适应度值f，持续进行寻优更新，直至搜寻的蜜源达到最大迭代次数Tmax.VMD算法的α值优化步骤如下：① 设定VMD参数α的范围；② 初始化ABC算法的相关参数，将C值作为适应度值；③ 以最优分解层数kopt运行VMD，全局搜索最佳的α值；④ 循环迭代至最大迭代次数，停止迭代，将蜜源的平均值作为VMD的最佳惩罚因子αopt.图1为改进VMD算法的流程图.

3 仿真信号检验

仿真信号x(t)由调幅信号x1(t)、调频信号x2(t)和正弦信号x3(t)组成，即

(10)

图1 改进VMD算法流程图

采样频率fs=2.0 MHz，采样点数N=4 096，图2为仿真信号的时域波形图，图中A为振幅，N为点数.

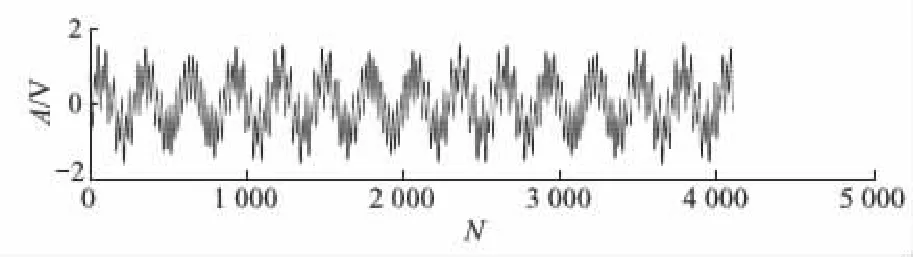
图2 仿真信号x(t)波形

取k为2～10，α=2 000，对仿真信号进行VMD运算，得到包络熵差异系数C随k变化的曲线，如图3a所示.从图3a中可以看到，当k=3时，C值最大，表明各IMF之间的差异较明显，VMD分解效果最优.因此，取最优分解层数kopt=3.

设置最大迭代次数Tmax=20，画出C随迭代次数T变化的收敛性曲线，如图3b所示.从图3b中可以看到，当T=8时，C开始收敛于1.785 4.将对应值2 555取作最优惩罚因子αopt.

取kopt=3，αopt=2 555，再次对仿真信号进行VMD运算，得到各IMF分量，并对其作傅里叶变换.图4a为各分量IMF1,IMF2,IMF3的时域波形和频谱，图中f为频率.从图4a中可以看到，仿真信号的3个主要分量均被准确地提取了出来，说明改进VMD算法实现了信号的自适应分解.为了便于对比，采用集合经验模态分解(ensemble empirical mode decomposition，EEMD)算法对仿真信号进行处理，得到各分量u1,u2,u3的时域波形和频谱，如图4b所示.从图4b中可以看出，EEMD算法也能有效地分解出信号模态.

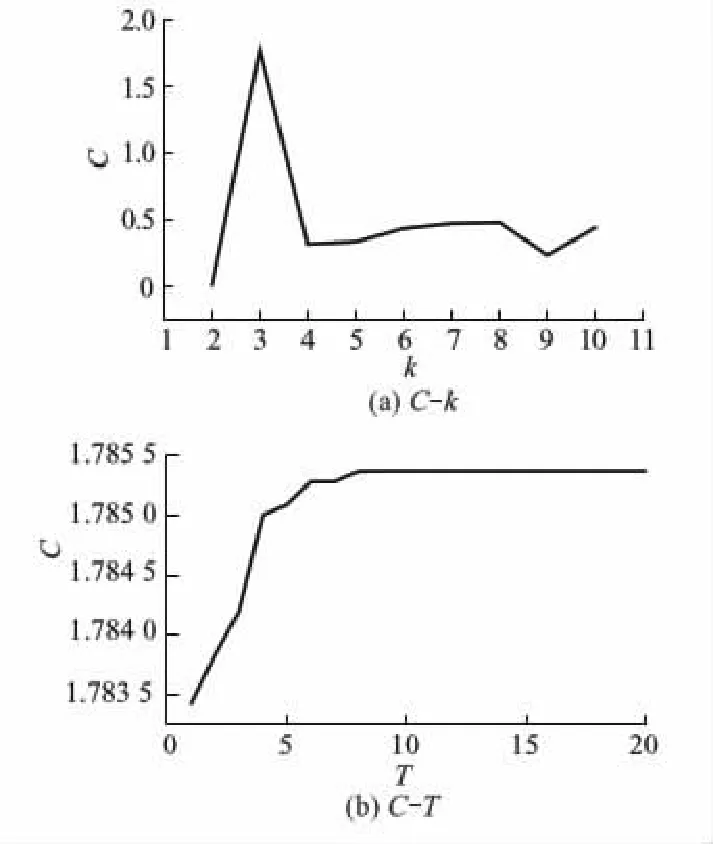
图3 仿真信号VMD参数优化

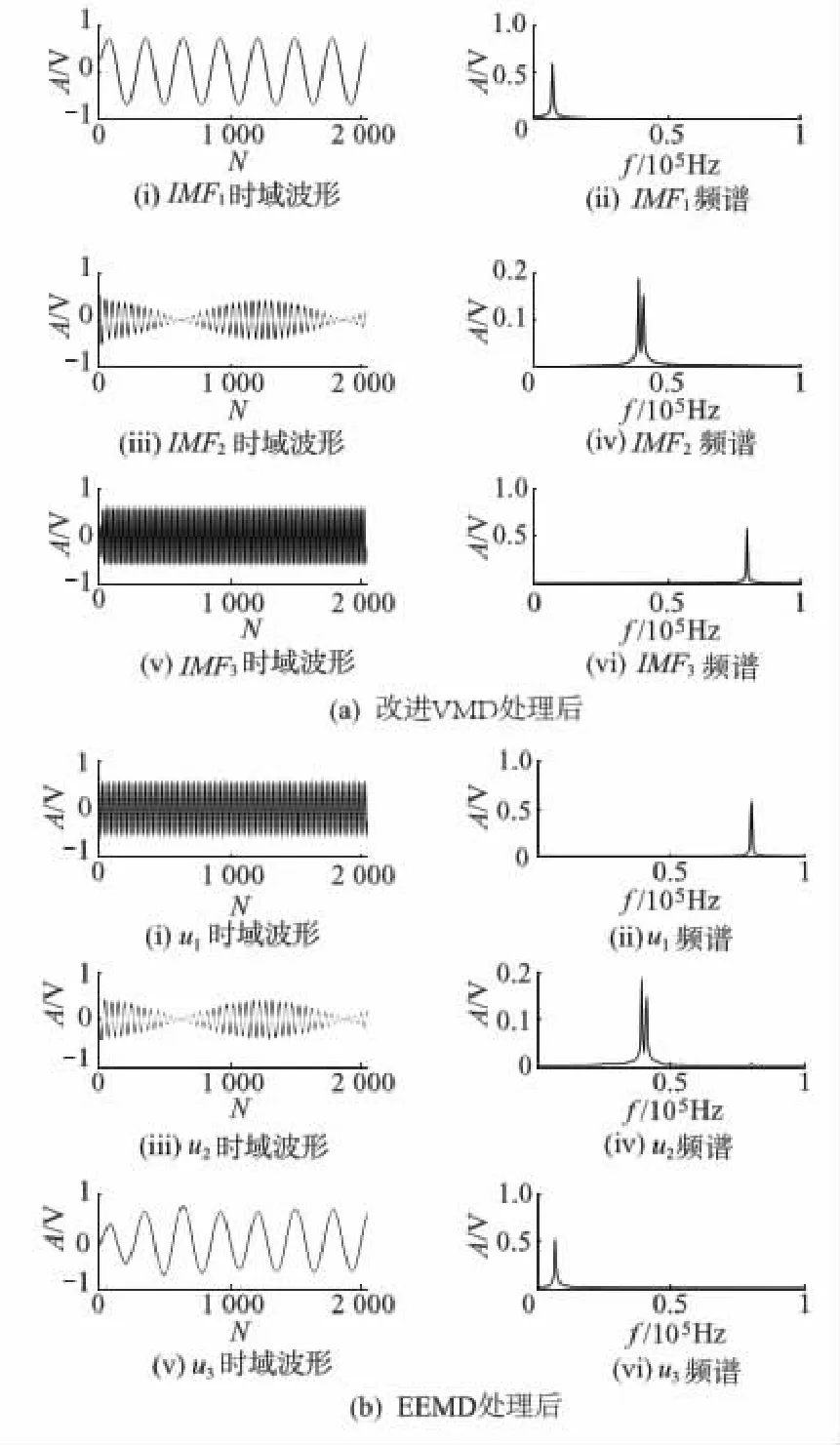
图4 改进VMD和EEMD处理后仿真信号的波形和频谱

为了进一步对比改进VMD和EEMD算法的分解效果，将比率误差作为评价指标，即

(11)

式中：Ek为分解得到的第k个分量的信号比率误差；dk为原始信号的第k个分量；dk为分解得到的第k个分量.Ek越大，说明信号分解得到的第k个分量与原始信号的第k个分量之间的差别越大，分解效果越差；反之，分解效果越好.

表1为2种算法分解后各分量的比率误差.

表1 改进VMD与EEMD的比率误差对比

由表1可知，改进VMD算法的各ESR值均明显小于EEMD算法，说明前者的分解效果更优.

4 试验数据分析

离心泵空化试验在某省级水力机械质量监督检验授权站的水泵试验台上完成.在试验的同时，采集相应工况下的AE信号.离心泵的额定流量Qr=20 m3/h，扬程H=42 m，转速n=2 900 r/min，电动机功率P=7.5 kW.2套SR-150M声发射传感器分别贴在靠近离心泵进、出口处的外壳上，AE信号采集与数据处理采用本课题组自主研发的AE信号采集与处理系统.试验系统及试验过程详见文献[4].图5为0.6Qr,1.0Qr,1.2Qr工况下的离心泵空化特性曲线，图中NPSH为汽蚀余量.

图5 离心泵空化特性曲线

限于篇幅，文中仅以0.6Qr工况下采集到的离心泵进口外壳处的AE信号为例，进行改进VMD运算.取空化特性曲线上的4个工况点Ⅰ，Ⅱ，Ⅲ，Ⅳ，分别对应于未空化、初生空化、临界空化和严重空化状态.取每个工况点的AE信号点数N=16 384，图6为相应的时域波形.图7a，7b分别为VMD分解层数k和惩罚因子α寻优过程.表2为4个工况点AE信号的改进VMD参数优化结果.

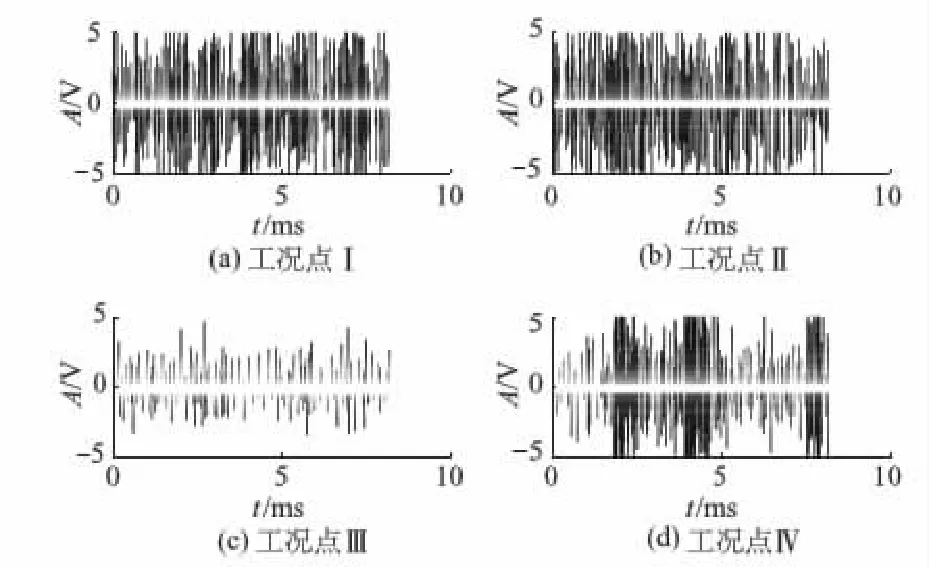
图6 4个工况点的空化AE信号波形

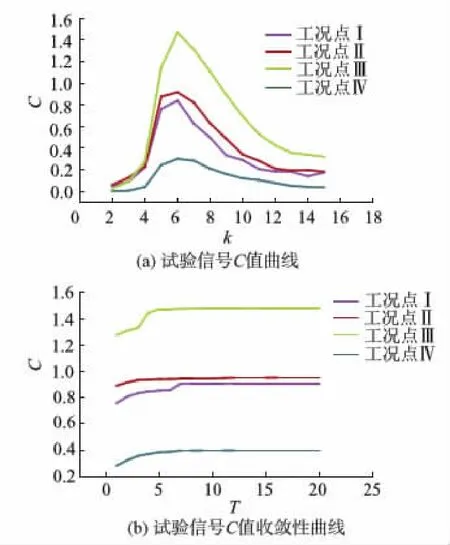
图7 试验信号VMD参数优化

表2 改进VMD的参数优化结果

图8为经改进VMD处理后，工况点Ⅲ泵进口外壳处AE信号各IMF的波形和频谱.

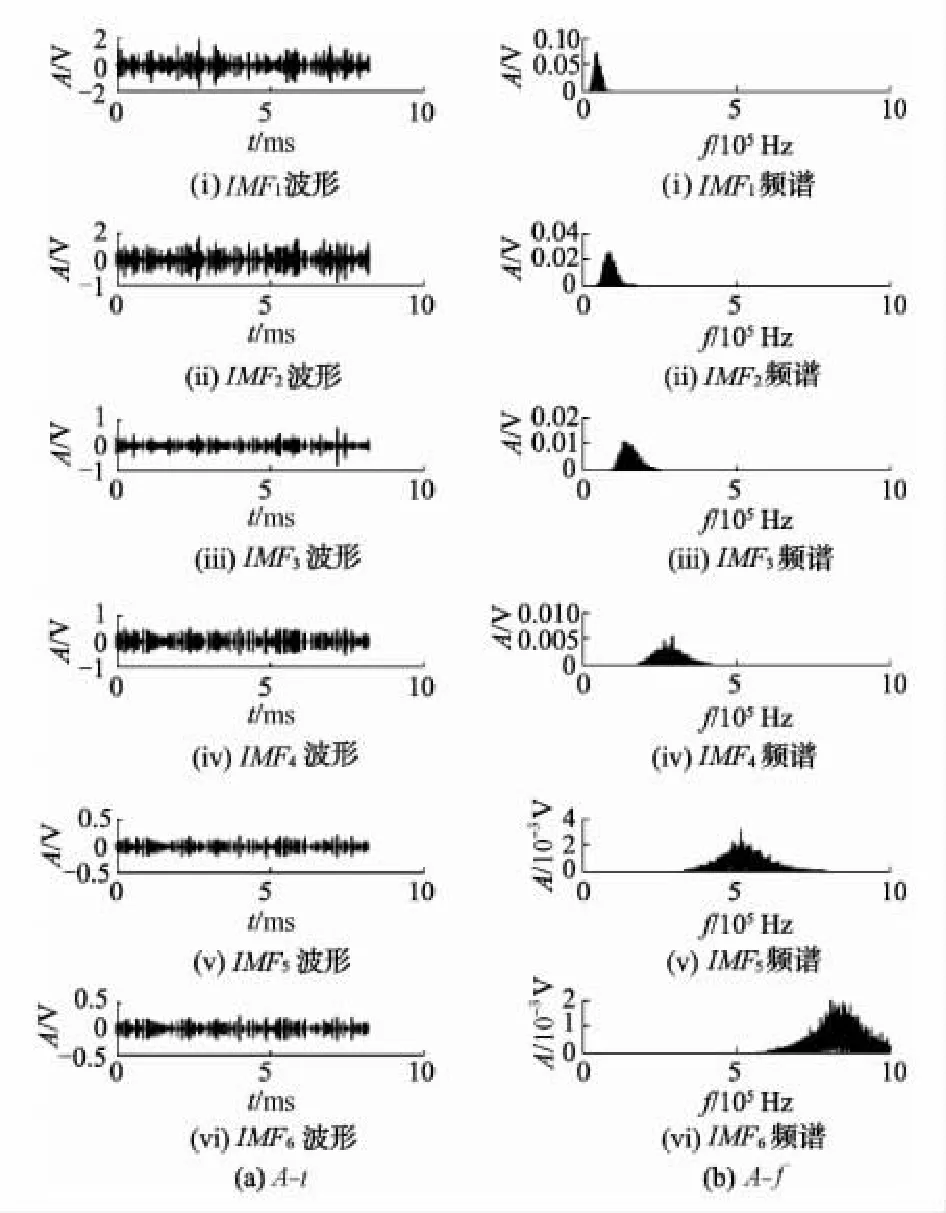
图8 工况点Ⅲ经改进VMD处理后的波形和频谱

为了更加细致地分析离心泵空化AE信号的变化规律，采用相关系数来揭示分解得到的IMF与原始试验信号之间的相关性，有

(12)

式中：x(t)为原始试验信号；IMFi为改进VMD分解结果中的第i层分量；ρx,IMFi为分量IMFi与原始试验信号x(t)之间的相关系数，其值越大，说明IMFi与x(t)的相关性越好，所携带原始试验信号的信息量越大.表3为4个工况点AE信号各分量的相关系数.

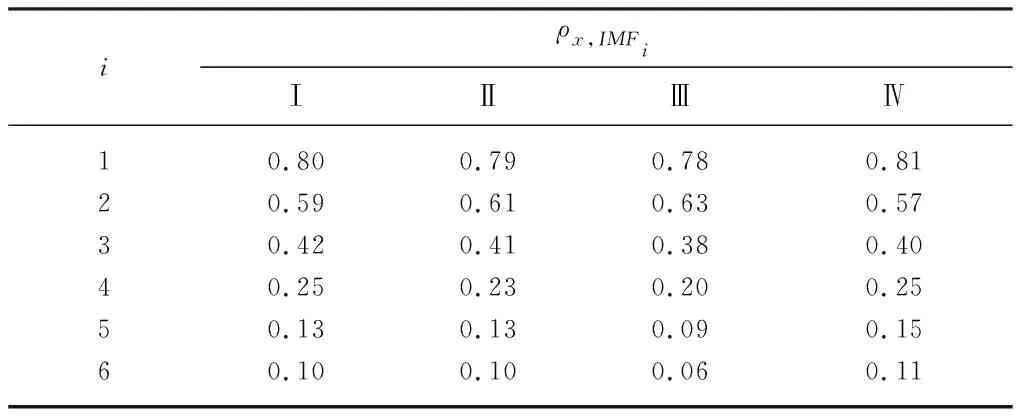
表3 各分量的相关系数

从表3中可以看出，4个工况点中IMF1与原始试验信号之间的相关系数均最大，IMF2的次之，即IMF1，IMF2与4个工况点的原始信号最为接近.图9为4个工况点分量IMF1和IMF2的频谱图.从图9可以看出，IMF1，IMF2的主要频率成分分别集中在50，100 kHz及其附近.该频率范围比文献[6]揭示的反映空化状态的AE信号特征频率范围更集中，也更准确.表4为4个工况点分量IMF1和IMF2的绝对能量值，分别记作Ea1，Ea2.

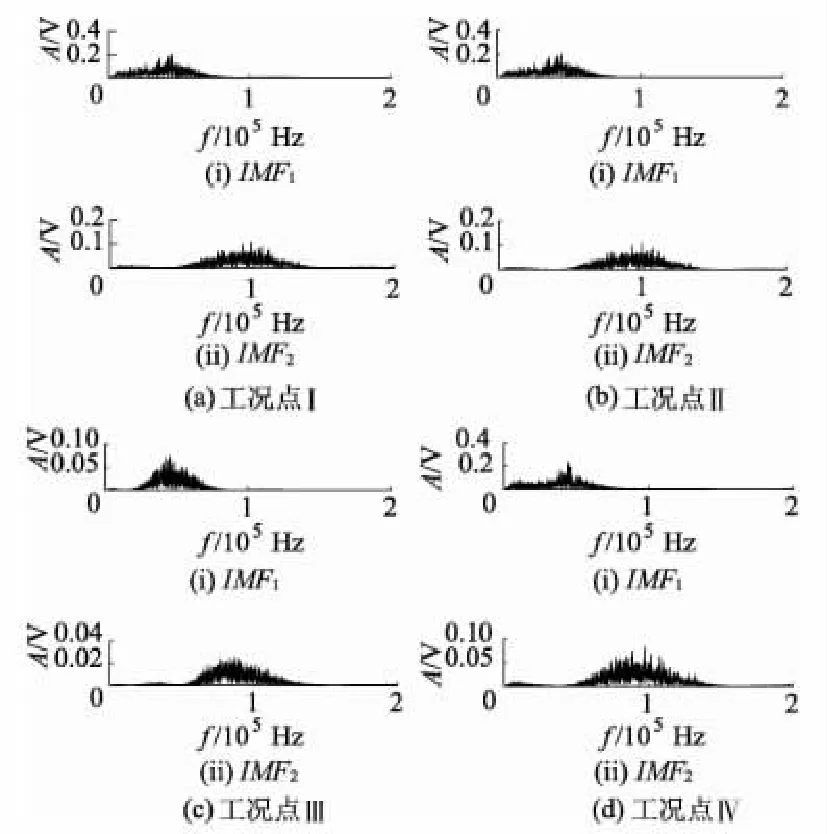
图9 分量IMF1和IMF2的频谱图

表4 分量IMF1和IMF2的绝对能量值

从表4中可以看出，随着离心泵空化从无到有、从弱到强的发展变化，以及NPSH值的不断减小，IMF1和IMF2的绝对能量值呈现“先保持基本不变—减小—变大”的规律.这是因为在工况点Ⅰ，Ⅱ，离心泵内的流体流动相对稳定，AE信号主要来源于水体流动，以及水流与离心泵内壁和叶轮叶片之间的相互作用.在空化初生点(工况点Ⅱ)，由于水流场中产生了少量空泡，IMF1，IMF2的绝对能量值略有减少.到临界空化点(工况点Ⅲ)，水流中的空泡不断增多，尺寸大小不一，且空泡之间相互撞击、产生内裂，引起气液两相流动，致使AE信号中IMF1，IMF2的绝对能量因被削弱或吸收而减小.至严重空化点(工况点Ⅳ)，离心泵内水流的扰动加大、紊流加剧，大量的空泡同时生成或溃灭，产生能量较大的高速微射流，撞击离心泵内壁和叶轮叶片，致使IMF1，IMF2的绝对能量大幅增加.因此，AE信号中IMF1，IMF2的特征频率范围和绝对能量的变化，准确反映了离心泵空化的发展变化状态.

5 结 论

1) 采用包络熵差异系数与ABC算法较好地解决了VMD算法中分解层数和惩罚因子这2个重要参数的优化选取问题，有助于实现非平稳信号的自适应分解.

2) 反映离心泵空化状态的AE信号特征频率范围分别集中在50, 100 kHz及其附近.随着离心泵空化从无到有、从弱到强的发展变化，这2个频率范围的信号分量的绝对能量值呈现“先保持基本不变—减小—变大”的变化规律.