基于强化学习算法原则的出行选择行为建模与仿真

赵思萌

(中铁第六勘察设计院集团有限公司，天津 300308)*

为了有效减缓高峰时段交通拥堵，一方面是改善交通基础设施，另一方面就是调控交通出行量 .调控交通出行量主要是调整出行者的出行时间和出行方式，即出行者避开高峰时段，采用公共交通方式出行，达到减少道路交通出行量的目的[1].

研究出行者出行时间选择和出行方式选择的文献较多，大多基于期望效用理论和离散选择模型[2-3].在一定时期内，出行时间选择和出行方式选择可以看作是一个动态学习和选择的过程，研究者往往注重行为决策和模型建立，而缺少对客观选择行为的轨迹模拟[4-5].本文基于强化学习算法原则，结合出行者出行行为选择的认知更新过程，构建了出行时间和出行方式联合选择的微观认知模型，并通过仿真的方法模拟出行者群体出行选择行为的变化规律，从而为交通管理等政策的制定和评估提供方法支撑，达到高峰时段减缓交通拥堵的目的 .

1 微观仿真方法

本文提出的研究方法主要包括两个部分：出行者个体和仿真系统.

1.1 出行者个体

在微观仿真方法中，通过对每个出行者的学习、适应以及行为决策过程进行建模，来描述出行者出行选择行为的过程，即将出行者作为一个智能体，通过积累经验和接受环境的变化对行为选择进行调整，这种方法通常可以拓展到多维的行为选择，如出行时间、出行方式、出行路径和目的地等[3].本文只研究了出行时间和出行方式的联合选择，更全面深入的研究将在后续中继续深入.

1.2 仿真系统

在完成单个出行者的行为建模后，将这些出行者输入到仿真环境中，给予出行者一定的属性，模拟出行者在实际交通状况变化下的学习、适应和决策过程，进而得到不同交通状况条件下的出行行为决策结果 .本文采用MATLAB编码实现出行者出行选择行为的仿真 .

2 模型建立

2.1 强化学习原理的引入

强化学习算法的基本原理是：如果智能体的某一行为使得环境对智能体回馈了正的奖赏(reward)，则智能体以后采取这个行为的趋势会加强[5-6]，其基本模型如图1所示 .

智能体与环境交互式，会遵循以下顺序事件[6]：

(1)智能体感知当前环境状态；

(2)智能体结合环境和当前状态，采取行为a；

(3)智能体执行a后，环境返回奖赏r；

(4)智能体更新自身状态值 .

本文将出行者选择出行时间所得到的节省时间和选择出行方式的节省的交通费用作为奖赏，同时引入学习因子和折扣因子，对出行者的认知过程进行建模 .出行者的出行选择行为一般分为两部分：一部分是认知更新和搜索，另一部分是决策选择[6]，原理图如图2 .

2.2 行为定义

假定出行者的每个选择都是基于先前经验积累才做出的，因此，定义一次出行方式选择或出行时间选择为一次行为[8]，用a表示，定义为：

a=(x,r,n,w)

(1)

式中：x表示一次行为的属性，本文指选择一个时间点出行或出行方式后的旅行时间及交通费用；r表示经过该事件后获得的奖赏(reward)；n表示该事件发生过的次数；w表示出行者对该事件的认知重要度 .

2.3 微观认知模型

2.3.1 出行方式微观认知模型

首先，建立出行方式的微观认知模型，模型中主要考虑的因素是出行方式的旅行时间和交通费用，用wi表示出行者记忆中对第i种出行方式的认知程度，定义为：

wi=θi·βi(i=1,…,m)

(2)

式中：θi表示该种出行方式在记忆中的重要程度；βi表示该出行方式在记忆中的衰减程度 .

当出行者选择某种出行方式后的实际情况与出行者期望效果越相近时，则会对该出行方式的记忆程度加深，即环境给予的回馈值更大；反之，则会对该出行方式的记忆程度降低[9].记忆程度θi定义为：

(3)

结合出行者以往对出行方式的选择情况，每一种出行方式会在出行者的记忆中形成优先级，优先等级不同的出行方式在出行者记忆中衰减的程度也不同，记忆衰减程度用βi表示，定义为：

(4)

式中：ranki表示第i种出行方式在所有出行方式中的优先级；γ为记忆衰减率(折扣因子)，取值为[0,1] .

2.3.2 出行时间微观认知模型

与出行方式选择的微观认知模型构建相似，出行时间选择的微观认知模型中仅考虑旅行时间作为影响出行者对出行时间选项的因素，用wj同样构建为：

wj=δj·φj(j=1,2,…,n)

(5)

式中：δj表示第j个出行时间点在记忆中的重要程度；φj表示第j个出行时间点在记忆中的衰减程度.

对出行时间点的记忆重要程度δj定义为：

(6)

同样，出行者对不同的出行时间点会形成不同的优先级，优先等级不同的出行时间点在出行者记忆中衰减的程度也不同，记忆衰减程度用φj表示，定义为：

(7)

式中：rankj表示第j个出行时间点在所有出行时间点的优先级；χ为记忆衰减率(折扣因子)，取值为[0,1] .

2.4 离散选择模型

2.4.1 Logit模型

在出行者通过经验积累后，会在记忆形成几个适宜的出行时间点或是出行方式，最后通过决策选择出对自己效用最大的，本文采用多项Logit模型来描述出行者的选择行为 .Logit模型通常用于计算个体在若干个可选方案中选择其一的概率，尤其是对一些影响选择决策且不能直接观测到的因素，可运用Logit模型进行分析，Logit模型的一般形式为：

(8)

最终计算考虑认知度下的加权选择概率如式(9)所示：

Pi′=Pi·wi′

(9)

2.4.2 效用函数的确定

(1) 出行方式效用函数

在第i种出行方式的选择上，其中以所选出行方式的旅行时间和出行交通费用作为考虑因素，建立第i种出行方式的效用函数Vi如下：

Vi=βT·Ti+βC·cosTi

(10)

式中：Ti为第i种出行方式的旅行时间；cosTi为所选出行方式的出行交通费用；βT和βC为模型待标定参数 .

(2) 出行时间效用函数

在出行时间的选择上，考虑了旅行时间和准时到达这两个因素，定义效用函数Vt为：

(11)

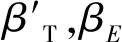
SAE(t,Tt,PAT)=max[(PAT-Tt-t),0]

(12)

SAL(t,Tt,PAT)=max[(Tt+t-PAT),0]

(13)

式中,PAT表示偏好出行时间 .

(3)本文采用调查问卷发放的方式收集数据，每份问卷分别设置2个出行时间选择场景和出行方式选择场景，由参与调研的人员完成，并记录每个参与调研者的基本出行信息 .其中两个场景示例如表1、2所示.

表1 出行时间选择示例

表2 出行方式选择示例

问卷选择在蜀汉路东地铁站、公交站以及附近小汽车停车场发放，最终共收回452份有效问卷，数据统计分析如表3所示，可以看出参与调查者以中青年为主，出行目的主要为上班群体，且上班旅行时间主要分布在10～30 min .

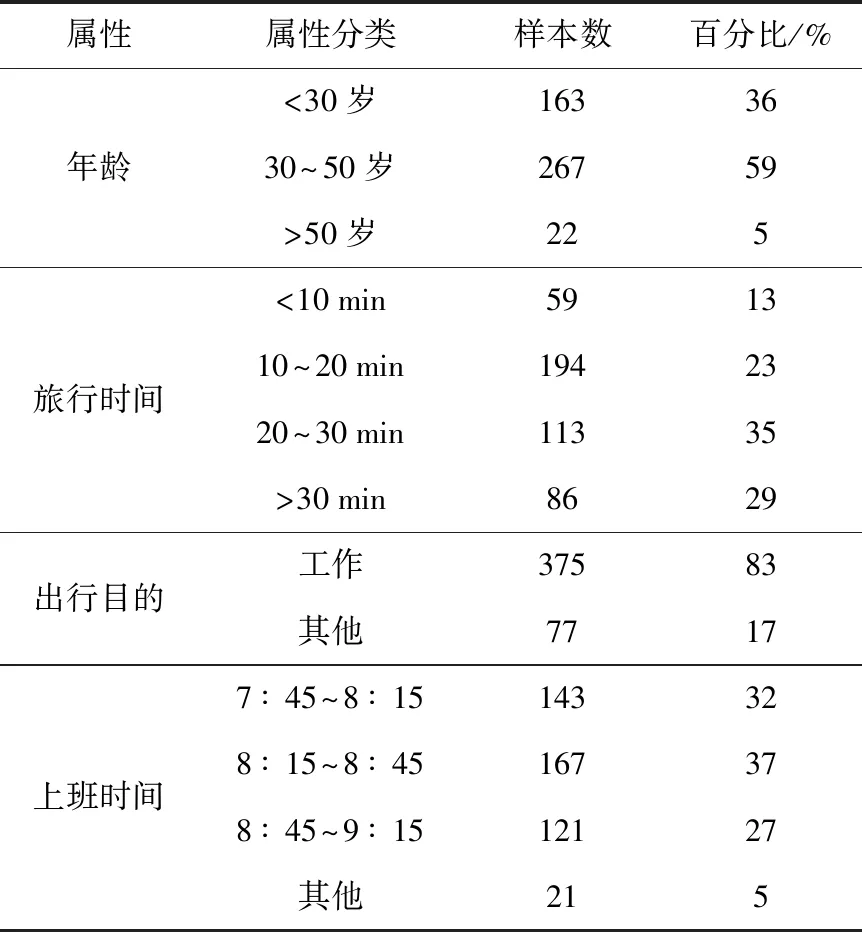
表3 调研数据统计

(4)模型参数标定

模型参数标定借助NLOGIT 5.0软件，标定结果见表4、5所示，由Pseudo-R2可以看出模型拟合度较好，t值表明待估计参数均显著[10]，且符号与预期一致 .

表4 出行方式选择模型参数标定结果

表5 出行时间选择模型参数标定结果

为了验证模型的精度，进一步收集了97份样本数据 .通过对比实际出行时间、出行方式选择和模型预测值，得到出行时间选择模型整体预测精度为86.4%，出行方式选择模型整体预测精度90.1% .同时，采用ROC(receiver operating characteristic curve)曲线说明模型的局部预测精度，如图3所示，可以看出两种模型的局部预测精度都较好，且出行方式选择模型的局部预测精度略好于出行时间选择模型[11].

3 仿真

本案例选取成都市的一段路程，线路如图4所示，以蜀汉路东区域为通勤人员的起点，以骡马市地铁站区域为目的地；其中通勤人员有三种出行方可供选择，分别是小汽车、公交车(341路)和地铁(2号线换乘1号线) .

3.1 仿真流程图

本案例仿真流程图如图5所示 .

3.2 案例说明

(1)本案例研究早高峰的交通状况，研究时段为7∶00～9∶00，将其以10 min为间隔分成12个时间区段，即11个出行时间点；

(3) 仿真参数设置如表6所示.

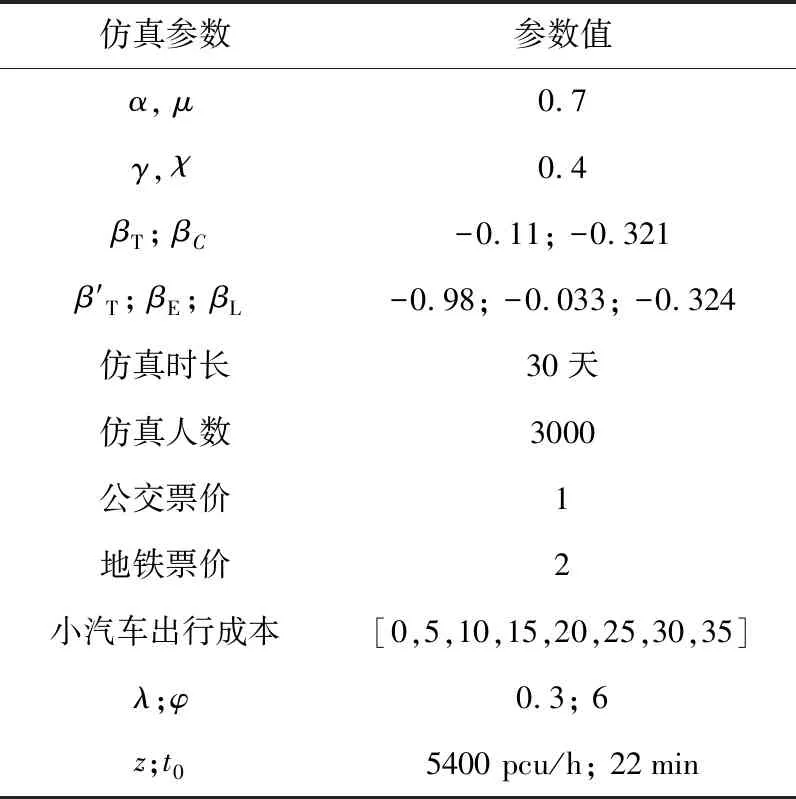
表6 仿真参数

3.3 仿真结果

通过仿真主要得到了两个结果：其一是出行者根据上班时间所做出的出行时间选择分布；另一个是在小汽车交通费用变化下的交通方式的转变 .

3.3.1 出行者出行方式选择分析

在出行方式的选择分析中，主要研究了在不同小汽车出行成本下出行者选择小汽车、地铁和公交出行的变化规律 .如图6所示，随着小汽车出行成本的增加，选择小汽车出行者逐渐减少，并且当小汽车出行成本达到15元以上时，小汽车出行者减少的趋势有所减缓，而公交和地铁出行明显呈上升趋势；其次，可以发现当小汽车出行成本设定为15元时，对小汽车出行者的限制效果最佳.

3.3.2 出行者出行时间选择分析

(1) 出行方式平均旅行时间

针对出行时间选择分布，本节首先对三种出行方式不同出行时间点的平均旅行时间进行了统计 .图7所示为小汽车出行成本为15元时的三种交通方式的平均旅行时间，可以看出：小汽车和公交受到道路通行能力的影响，出行时间呈现高峰现象；而地铁为轨道运行，运行时间较为平稳 .

(2) 出行者出行时间选择对比分析

图8、图9分别给出了小汽车出行成本为0元时和15元时的出行时间选择分布图 .对比发现：小汽车出行成本为0元时，9∶00上班的人群选择8∶40和8∶50出行较为集中，通过旅行时间判断为选择小汽车作为出行方式；而当小汽车出行成本为15元时，9∶00上班的人群选择8∶40和8∶50出行的次数明显减少，选择其他时间点出行的次数稍有增加，整体出行时间分布向均匀化转变，进一步缓解局部时间段的拥堵状况 .

对于SP调研数据，在小汽车出行成本为15元的条件下，仅有13%的调研者选择了小汽车出行 .而对于仿真结果，当小汽车成本为0元时，汽车出行方式占了近60%，而当成本为15元时，汽车出行下降至8%，可以看出仿真结果与SP调研数据显示的出行行为偏好一致，但模拟精度还存在一定的偏差，可能是模型参数标定的误差所致.在后续研究中，应进一步完善场景实验和属性水平设计，提升模型参数标定的精确度 .

4 结论

仿真结果表明：

(1)随着小汽车出行成本的增加，部分小汽车出行者逐渐选择公共交通出行，并且当出行成本增加到15元以上时，出行方式选择变化趋于平缓；

(2) 出行者的出行时间选择分布趋于均匀化，进而减缓局部时间段的拥堵状况 .

本文的研究成果可以为减缓高峰时段交通拥堵以及制定和评估交通管理等政策提供方法支撑.