航天器姿态控制的区间参数化方法*

汪 洋，龚 薇*，张江伟，余 琪，朱勃帆

0 引 言

航天器姿态控制是航天器执行空间任务中重要组成成分，由于航天任务的多样性，在空间任务执行过程中，实现快速有效的控制显得格外重要.通过给定驱动力矩，使得航天器姿态达到期望姿态是航天器姿态控制的主要任务.

在处理航天器最优控制问题上，一般被分为间接法和直接法，间接法是基于一阶最优性条件来解决问题，直接法是解决最优问题的近似问题[1].在解最优控制问题的近似问题的方法中，有两种常见的方法，一种是将外部控制表示为时间和一系列参数的显示解析函数，通过逆动力学粒子群优化技术(IPSO)来解决最小时间机动问题[2-4]，另一种是将控制按照一定规律的近似值处理,如基于粒子群优化[5,6]，伪谱法优化[7]，混合二阶段法[8].

解决最优控制问题的近似问题时，最优控制问题的数值解都要从无限维的优化问题转换到有限的参数优化问题[9].虽然文献[5-8]都给出了满足约束的航天器的最优控制的数值解，但是最优控制问题的数值解切换时间点的问题并没有考虑到.时间变换的方法[10,11]可以解决这样的问题，但是过多的时间切换节点将导致计算量的迅速攀升.并且，在解决最优控制问题中，无效切换时间点是需要避免的.

本文考虑了航天器姿态的最优控制问题，提出一种新的区间参数化的计算方法，此方法如下所述：首先将航天器姿态控制的能耗，以及系统的收敛速度等性能指标建立为目标函数，考虑实际过程中的物理限制，例如陀螺仪测速限制的角速度约束，以及反作用轮的实际输出限制等作为有界输入和有界状态约束.在解决这样的最优控制问题的时候，一种控制参数化的方法被使用[12-16]，控制值将由分段常值函数表示，解决该问题的近似问题.在解决连续状态不等式约束的时候，采用约束转录法[17]与局部平滑法相结合来处理连续状态不等式约束． 经过这样的处理，原约束变为一个标准约束的形式.同时问题的可行域也会随之变化，通过[9]提出的渐近调整相关参数的方法来解决.

在解决切换时间的问题上，一种新的区间时间变换的方法被提出，通过改变各个子区间长度，间接的使得切换时间点线性变换，从而解决最优问题切换时间点确定的难题.在经过上述处理以后，此问题可以作为数学规划问题，由任意一种优化方法解决.一种基于梯度的miser3.2[18,21]软件被用来解决这样的问题，并给出了相关的代价函数以及约束的梯度公式.数值仿真表明，提出的方法是有效的.

1 航天器姿态控制的模型以及问题描述

在相对于惯性坐标系的本体坐标系下，航天器的运动学和动力学模型可以由以下的公式表述[19]：

设x1(t)=q1(t)，x2(t)=q2(t)，x3(t)=q3(t)，x4(t)=q0(t)，x5(t)=ω1(t)，x6(t)=ω2(t)，x7(t)=ω3(t).

则卫星姿态控制的动力学方程为：

考虑如下的二次型性能指标的代价函数：

(3)

并且在实际的空间任务中，一般需要限制控制转矩和角速度完成卫星姿态机动过程[20].

考虑航天器反作用轮的输出物理限制，限制反作用轮输出力矩在0.4 N·m，引入如下控制约束：

另外考虑到陀螺仪的测速饱和，限制航天器的转动角速0.2 rad/s,引入如下的状态约束：

因此航天器姿态控制的最优化问题可以表述成问题P的形式：

(4)

2 控制参数化

问题P是一个带有连续状态不等式约束以及终端约束非线性最优控制问题，传统的最优控制理论解决这样的问题是非常困难的.一种控制参数化的方法被提出用于解决这样的带有连续状态不等式约束的最优控制问题.控制参数化将一个无限维的最优控制问题转化为一个有限维最优参数选择问题，后者更容易解决[12-16].

对于k=1,2,…,p一个分段常值函数将作为控制的p段组成成分，控制值切换时间序列为：

τ=[τ0τ1…τp]T

其中，τ0=0，τp=tf

控制将由如下函数的表达式近似：

其中，σk表示分段控制值，χI(t)是指示函数，其定义为：

其中，I表示σk对应的时间区间.

经过如上的变换原问题P转换成一个最优参数选择问题Pc.

尽管控制参数化的方法是可行的，但是寻求的最优控制是一个分段常值函数.显然，对这个分段常值函数来说，切换时间点是未知的，如何精确的确定切换时间点是一件十分麻烦的事情.切换时间点变换的方法有效的解决了这个问题，将切换时间点作为决策变量进行求解，能够有效的求出实际控制的最佳切换时间点.

3 切换时间点变换

切换时间点变换法[10,11]是将切换时间点τi,1≤i≤p-1作为待优化的控制参数进行优化.

为此，一个新的时间映射s∈[0,1],构造一个从时域t∈[0,tf]的固定切换时间点k/p,k=1，2…,p到的s∈[0,1]可变时间切换点的变换.

定义如下的微分等式进行变换：

初始条件：

t(0)=0

其中，θi≥0,i=1,2,…，p.

通过对式子以及初始条件积分，对于s∈[(k-1)/p,k/p),k=1,2,…,p有：

4 区间时间变换

值得注意的是，随着控制段数的增加，切换时间点数量随之增加，这将导致这个问题的计算量迅速增加.因此，区间时间变换的方法被提出用于有效减少计算切换时间点.

区间时间变换方法，将控制切换的时间序列分为不同的子区间，通过改变子区间的长度，使得子区间内的控制切换时间随区间长度线性变化，从而达到改变各个子区间控制值的切换时间的目的.在减小计算量的同时，优化控制值切换时间.如图1所示，传统的时间切换点变化技术，是将每一个时间切换点进行计算,如图1红线所示，而区间时间变换方法是将时间分为若干个子集(子集中的切换时间点等分)，优化每个子集的所占的时间长度，然后对单个集合等分延伸控制时间节点，如图二黑线所示.

图1 时间变换方法Fig.1 Time transformation method

因此，以控制切换时间序列分为三个子区间为例，将控制值进行分区间处理，

定义如下的区间：

U1=[0,p1/p),U2=[p1/p,(p2-p1)/p),

U3=[(p2-p1)/p,p3/p],

V=[(k-1)/p,k/p),k=1,2,…,p

定义如下的微分等式进行变换，

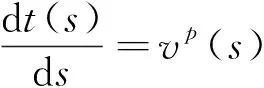
(5)

显然可以得到，当s∈V时，有：

利用上述的微分等式(3)，可以对上述控制系统f(x,u)进行一个新的时间变换：

=vp(s)f(x(s),u(s))

可以证明，经过如上的变换，Pc变换成问题Pt.

可以证明如上的变换的满足最优解的收敛性定理.其证明过程类似文献[11]中的定理一和定理二.

5 连续状态不等式约束的计算方法

在本节中，应用约束转录结合一种局部光滑的方法来处理不等式约束.

首先，将连续状态不等式约束等效为如下的等式约束：

Gi(σp,θ1,θ2,θ3)=

i=1,2,…,6

由于等效的约束函数不可微，因此对于每个i=1,2,…,6，都用光滑函数(4)来近似.

式中给出的ε>0为可调参数，所以式子可微，但是可行域不同，因此需要应用参数调整渐进的方法来解决.具体而言，对于每一个i=1,2,…,6,设

(6)

Gi,ε(σp,θ1,θ2,θ3)=

于是将其替换后得到问题Pε

利用数值法求解问题Pε，得到的最优解不满足(2)的约束规范.于是引入如下等式：

Gi,ε,γ(σp,θ1,θ2,θ3)=-γ+Gi,ε(σp,θ1,θ2,θ3)≤0

替换得到问题Pε,γ

可以证明上述的变换满足最优解收敛定理，其证明过程类似文献[9]中的定理8.3.1和定理8.3.3，给出如下算法近似地解问题P

对于任意的γ>0，ε>0，在此问题中取ε=10-1，γ=5ε/16，εmin=10-3；

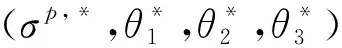
第三步：若第二步满足转至第五步，否则转至第四步；

第四步：令γ=γ/2，转至第一步；

第五步：令ε=ε/10，γ=γ/10，转至第一步，当ε≤εmin时，算法停止.

6 代价函数和约束的梯度公式

提出一种通过代价函数和连续状态不等式约束对u的梯度求解问题Pε,γ的计算方法，为了求解每一个u对应的代价函数和连续状态不等式约束的梯度，给出以下两个定理.证明过程均类似文献[9]中的定理5.2.1

定理1.代价函数的梯度公式为：

k=1,2,3

其中，H0(x,σp,θ1,θ2,θ3,λ0(s))为哈密尔顿函数

H0(x,σp,θ1,θ2,θ3,λ0(s))=

协态方程的解：

边界条件为：

(λ0(1))T=0

定理2.连续状态不等式约束函数的梯度公式如(5)，(6)所示.

(7)

k=1,2,3

(8)

其中，Hi(x,σp,θ1,θ2,θ3,λi(s))为哈密尔顿函数.

Hi(x,σp,θ1,θ2,θ3,λi(s))=Gi(x,σp,θ1,θ2,θ3)+

协态方程的解：

边界条件为：

(λi(1))T=0

7 计算结果与仿真

本文选用反作用轮为动力机构的航天器姿态控制问题，考虑实际过程中的输入有界约束，以及角速度有界约束，验证算法的有效性，取：

选取初始点θ=[100 100 100]，u=[0 0 0]，初始姿态Q0(t)=[0.512 0.765 0.14 0.3647]T，期望姿态，Qd(t)=[0 0 0 1]T.在(1)中的权值矩阵为Q=diag{100,100,100,100,10,10,10}，R=E进行仿真测试.

最终得到最优区间映射值，θ=[75.7786 151.905 83.093]，最优值2.972.最优控制输入值如图4所示.其状态响应曲线如图2，图3所示，角速度值和控制值均满足实际的物理约束.仿真采取30段控制值近似，若通过全时间切换节点计算，将要计算30个切换时间节点变量，通过区间变换的方法，只需要计算3个区间长度变量，计算的决策变量数，只需要占到10%.其控制响应曲3如图所示，控制值变化区间，第一个区间内，变换时间间隔小，此时变化幅度较大，在第二个区间，控制转矩的变换幅度较小，或基本不变，此区间较长，在第三个区间，控制转矩小幅频繁变化，变换时间间隔较小，实现了区间时间变化，所得到的子区间长度是最优的，验证了方法的有效性.

图2 最优控制下的四元数响应曲线图Fig.2 Quaternion response graphs under optimal control

图3 最优控制下的角速度响应曲线Fig.3 The angular velocity response curves under optimal control

图4 最优控制转矩Fig.4 Optimal control torques

8 结 论

本文研究了一类航天器姿态控制问题，通过区间化的参数化方法，最优控制解的数值解由一系列不固定的切换时间点的分段常值函数近似，提出的区间时间变换方法，相比传统的定区间长度，以及时间变换方法，本方法在确定最优切换时间基础上，减小了切换时间点的计算量.并且考虑了实际执行过程中的物理约束，运用了约束转录和局部平滑的方法处理了连续状态不等式约束.得到的最优控制问题的近似解接近最优解并且最优解满足实际工作情况，因此在实际执行过程中，可以当作控制的初始估计，或者作为参考值，具有较大的使用价值.