基于深层循环神经网络的陀螺仪降噪方法研究*

井小浩，贠卫国，韩世鹏

0 引 言

陀螺仪是一种角速度传感器，通常用来测量运动物体相对于空间转动的角速度或角位移，也可以通过陀螺仪实现物体姿态或者运动轨迹的测量和控制.陀螺仪作为惯性导航系统的重要组成部分，它的发展对我国的国防科技，航海业，工业等具有十分重要的战略意义[1].目前陀螺仪有激光陀螺、光纤陀螺陀螺仪、微机电陀螺仪等，在航天、航空、武器装备、自动驾驶、手机、娱乐设备等诸多领域得到广泛应用，但是目前陀螺仪受限于设备体积、元件材料、环境因素等，陀螺仪精度差依然是制约其扩大应用发展的重要因素.

近年来，国内外专家对陀螺仪一直持续不断的研究，包括硬件改进和软件算法改进两大部分，硬件改进成本高，耗时久；软件算法改进，成本低，耗时短，大量学者在算法改进方面做了很多工作.从卡尔曼滤波[2]到小波分析、传统神经网络[3]、SVM支持向量机[4]方法，都不同程度地应用在陀螺仪信号质量提升上，但是这些方法都存在一定的缺陷，卡尔曼滤波优点是可以实时处理不需要存储大量数据，但该方法是在平稳序号下建模的，而陀螺仪输出的大多是不平稳信号，无法自适应地估计不同环境下陀螺仪噪声特性；小波函数的优点是滤波速度相对较快，然而针对陀螺仪的输出数据变化不明显导致小波尺度难以界定；支持向量机的优点泛化能力强，有效的抑制随机噪声，但支持向量机对大规模问题难以实施，而且消耗机器内存及运行时间；深度循环神经网络是一种专门针对时间序列信号处理的算法，在时间序列信号处理方面有不可比拟的优势.陀螺仪输出信号具有时间序列特点，随着时间输出误差会越来越大，同时循环神经网络也是基于大规模数据，数据模型的训练也不依赖数据变化微小和环境不同，能够克服以上问题，本文提出采用长短记忆神经网络(LSTM)[5]结合门循环单元(GRU)[6]进行陀螺仪输出信号的滤波降噪，并分析不同网络对滤波效果的影响.循环神经网络作为一种常用算法，在处理分类[7]和回归[8]两大问题上有很好的应用，而它的变体LSTM和GRU以其特殊的细胞结构被广泛应用在处理时序问题上[9-10].

本文针对陀螺仪的随机误差，先使用Allan方差进行预分析，然后提出了一种不同网络层进行连接的方式，考虑到脏数据影响实验效果，数据经预处理后进行补偿处理.对比分析几种不同网络的损失函数、标准差和随机误差，并进行了补偿.

1 误差模型

1.1 Allan方差辨识误差

陀螺仪产生的随机误差主要包括角度随机游走ARW、量化噪声QN、偏差不稳定性BI、速度斜坡RR、速度随机游走RRW等噪声.通过Allan方差可以将陀螺仪产生的几种噪音进行分离，利用双对数曲线可以直观的反应出几种不同噪音的大小.

量化噪声QN是信号经过离散化数字信号与实际模拟信号的差值.从频率来看这类噪音属于高频噪音，在陀螺仪输出时，通过电路转换将模拟信号转换为数字信号而产生的一种随机误差.

量化噪音的Allan方差：

(1)

式中，Q为量化噪音误差系数：τ为采样周期.

角度随机游走ARW，是对信号积分的结果.当陀螺输入为零时，输出的角度随机游走为随机函数与白噪声的叠加.

角度随机游走的Allan方差：

(2)

式中，N为角速度随机游走误差系数.

零偏稳定性是指低频零偏抖动，产生的原因是内部电路信号不稳定形成波动，代表零偏随时间变化的情况.

零偏稳定性Allan方差

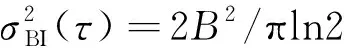
(3)

式中，B为零偏稳定性的误差系数.

速度随机游走RRW作为不确定噪声源的随机噪声，是由于对角速度的功率谱进行积分所致，是一种相关噪声长时间的无源随机过程.

速度随机游走Allan方差

(4)

式中，K为速度随机游走系数.

速度斜坡表示的是随着时间变化，陀螺仪的信号变化非常缓慢且是一个单调的过程，输出角速度变化也比较小.

速度斜坡Allan方差

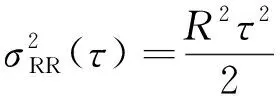
(5)

式中，R为速度斜坡误差系数.

Allan总误差[11]为

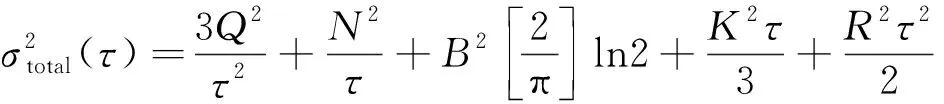
(6)

通过Matlab进行曲线拟合可以得到各项系数，然后可计算各个随机误差.

2 循环神经网络神经

2.1 长短记忆神经网络

长短记忆神经网络是循环神经网络的一种特殊结构，可以学习到长期依赖的信息，应用在陀螺仪这种随着时间漂移误差越来越大的数据建模中，非常切合实际.

如图1所示是LSTM结构模型[12]，从图1可以观察到LSTM相对于RNN其结构上对于每个细胞核引入了三个门，分别是输入门、遗忘门、输出门，通过门的开闭和记忆单元的更新，赋予了网络可变的记忆长度，通过输入门可以更新单元值，信号经过遗忘门通过神经元激活函数可以把数值映射在0到1的区间里，这种结构改进来源于人脑的记忆状态，可以有选择的保留有用的信号，而忘记那些对网络而言作用不大的信号，输出门作为隐层状态用于下一个单元的输入.

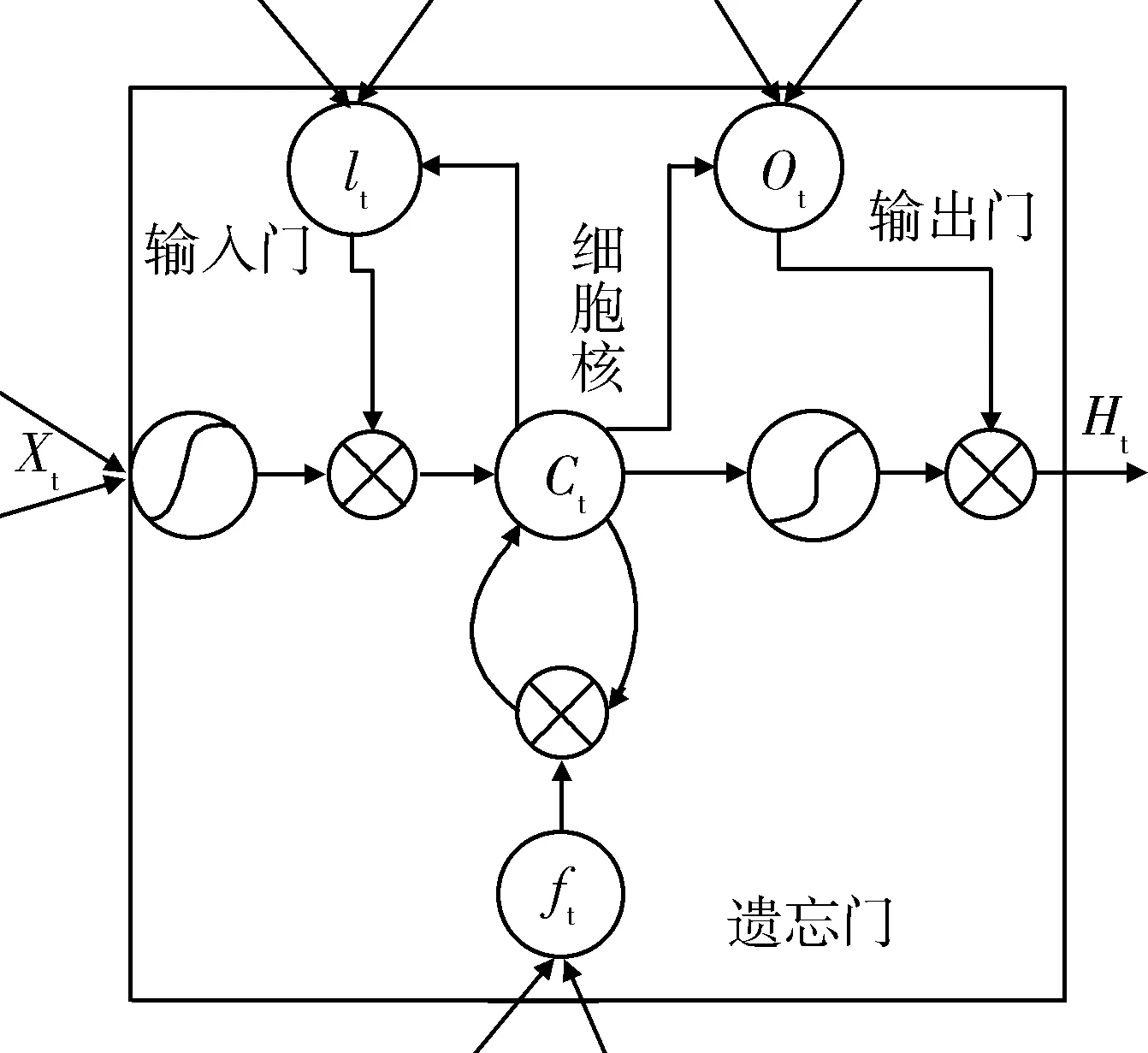
图1 LSTM网络结构图Fig.1 LSTM network structure diagram

各门的控制信号输入和更新权值公式如下[13]：

遗忘门：

ft=σ(wf·[ht-1,xt])+bf

(7)

式中ht-1表示上一个核的输出，xt表示当前细胞的输入，σ表示sigmod函数，bf表示遗忘门的偏置.

输入门：

it=σ(wi[ht-1,xt]+bi)

(8)

ct=tanh(wc[ht-1,xt]+bc)

(9)

式中,wi表示输入门的权重，bi表示输入门的偏置，wc表示细胞核的权重，bc表示细胞核的偏置.

输出门：

ot=σ(w0[ht-1,xt]+bo)

(10)

ht=ottanh(ct)

(11)

式中,wo表示输出门的权值，b0表示输出门的偏置.

当信号在t时刻时，接受到当前状态的xt，和上一时刻(t-1)的隐层状态的输出ht-1，作为整个神经网络单元的输入，分别与输入门、输出门和遗忘门的权值和偏置结合，得到输入门、输出门、遗忘门的信号，然后根据当前信号，更新记忆细胞ct，和当前时刻的ht，并将其作为后续信号的输入，反复训练次过程，LSTM网络能够自发的学习到各个门单元的最佳权值和偏置项，相对于RNN网络，LSTM能够选择性的保留信息，很好的解决了长期依赖信息而产生的梯度爆炸和消失.

2.2 门循环单元(GRU)

GRU不仅很好地解决了神经网络的梯度消失和梯度爆炸问题，同时相对较少的参数使训练过程能够更快一些.如图2是GRU单元结构[14]，GRU有两个门控单元,更新门和重置门，通过一个更新门就可以同时进行遗忘和选择记忆.

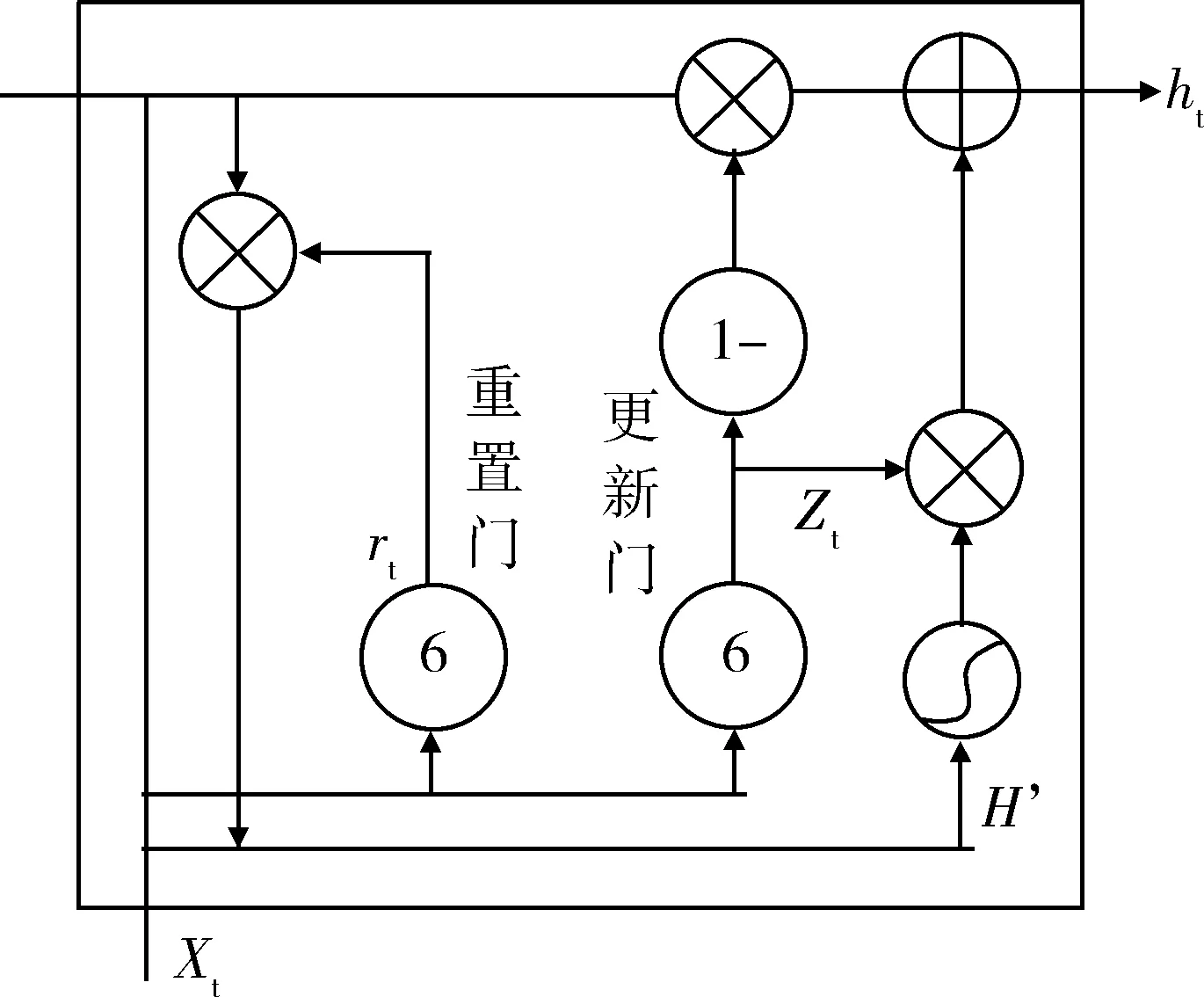
图2 GRU网络结构Fig.2 GRU network structure

各门的控制信号输入和更新权值如下：

重置门门控：

rt=σ(wr[ht-1,xt])

(12)

式中，ht-1表示上一个核的输出，xt表示当前细胞的输入，σ表示sigmod函数，wr表示重置门的权重.

更新门门控：

Zt=σ(wz[ht-1,xt])

(13)

式中，wz为更新门权值.

重置表达式：

h′=tanh(w[rt⊗ht-1,xt])

(14)

式中，w代表候选状态需要记住记忆权值，

更新表达式：

ht=(1-z)⊗ht-1+zt⊗h′

(15)

式中，zt更新门信号，h′候选状态下的信号.

通过上一个状态t-1时刻的输出ht-1和当前节点的输入获取两个门控单元，然后通过重置门控重置之前的数据，与当前信号输入拼接，通过激活函数tanh得到当前输入的有效数据，相当于LSTM的记忆单元.更新门的门控是0到1，门控越接近1代表记忆下来的东西越多，接近0遗忘的东西越多.然后通过更新表达式，就可以得到当前时刻的ht.并将其作为信号输入，反复训练可以得到权值和偏差项.

2.3 算法流程实现

由于陀螺仪的三轴输出数据随着时间的变化随机误差会越来越大,所以我们选择基于时间序列的循环神经网络来实现信号降噪.本文基于多层的网络模型进行构建，对比几种不同的神经网络连接，找到更适合陀螺仪数据降噪的神经网络模型.该算法模型如图所示，有4个功能模块包括输入层，隐藏层，输出层，网络模型训练层，在输入层我们对数据集进行划分，标准化数据，定义神经网络参数.在隐藏层搭建网络模型LSTM-LSTM和LSTM-GRU两种深层神经网络.在网络训练层使用均方值求损失函数，梯度下降法更新权值和偏置.输出层预测陀螺仪输出数据.

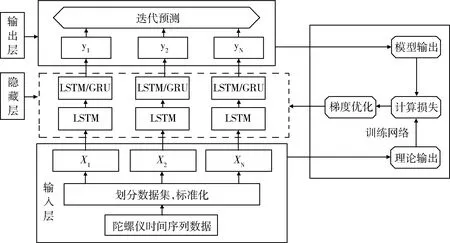
图3 实验流程图Fig.3 Experimental flow chart

2.3.1 LSTM-LSTM网络模型

该网络模型结构图如图4所示，隐藏层用双层LSTM，经过输入层处理后的原始数据进入隐藏层把数据给第一层LSTM网络，第一层网络的输出ht-1成为了第二层网络的输入，结合上述对LSTM单元结构的介绍，该网络能够记住陀螺仪长期的有效特性和短期的有效特性，通过添加网络的深度，加深网络的学习记忆，提到训练效率，进而获取更高的准确率.

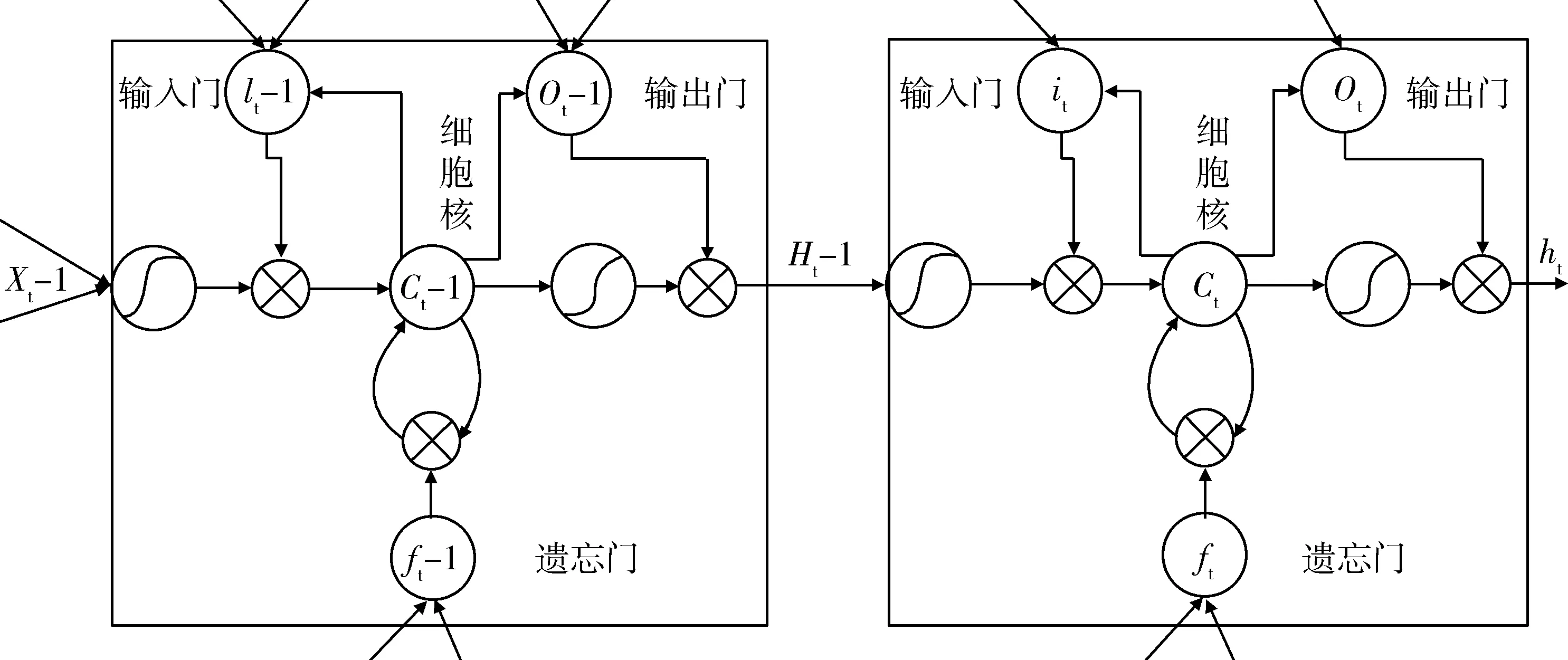
图4 双层LSTM网络结构实现Fig.4 Implementation of a double-layer LSTM network structure

2.3.2 LSTM-GRU网络模型

LSTM-GRU网络结构搭建是对双层LSTM的一种改进，与双层LSTM类似，不同点在于在隐藏层的第二层使用GRU神经网络单元，这是基于GRU网络的LSTM-GRU网络算法，如图5所示，采用两种不同的网络单元对数据进行训练.

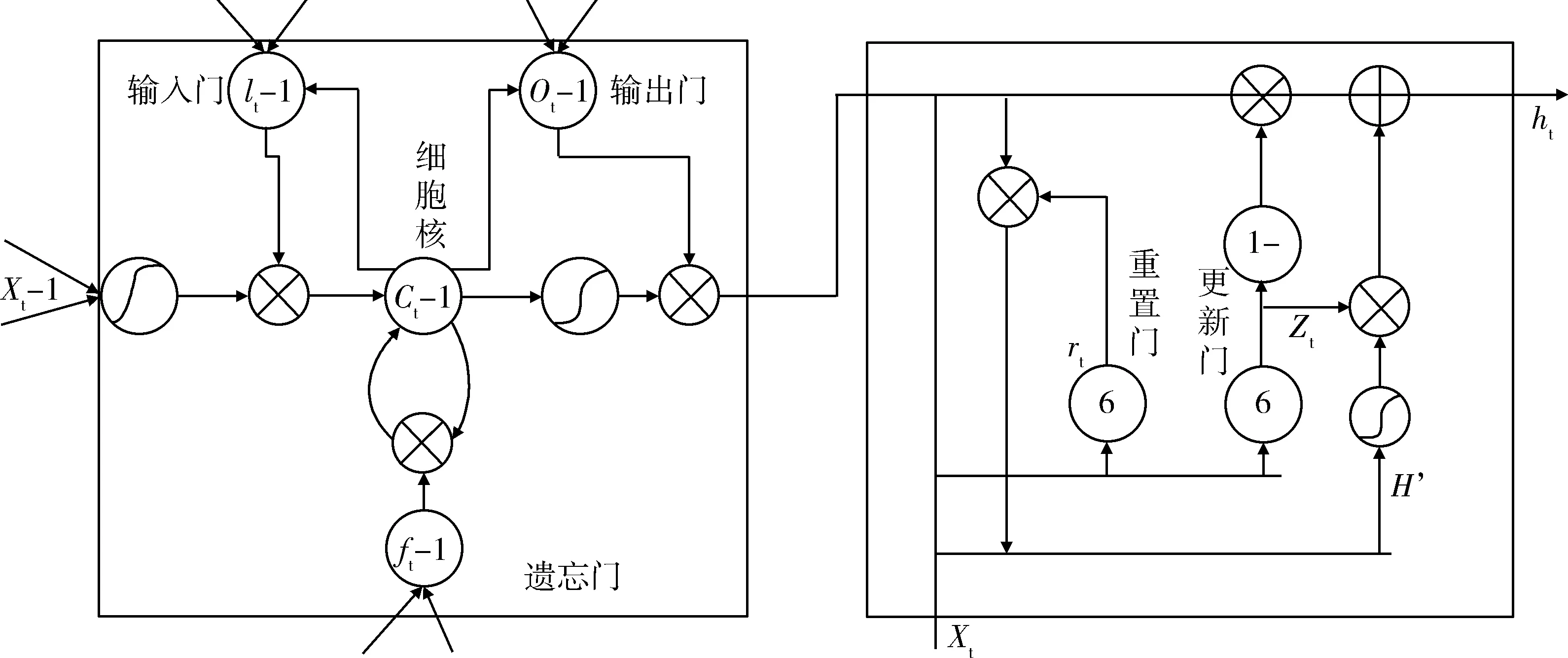
图5 LSTM-GRU网络结构实现Fig.5 LSTM-GRU network structure implementation

3 实验验证

针对本文提出的算法，采用X/Y/Z轴陀螺仪的真实输出数据作为实验数据集，利用上述对两种网络描述的相关理论，并针对不同网络进行模型搭建.通过对比几种不同网络得到不同的预测结果和相应的损失函数，进一步对循环神经网络的几种变体进行研究，最后通过Allan方差辨识陀螺仪的几种随机误差，找出本实验中最优的解决方案.整体框架如图6所示：

图6 整体框架图Fig.6 Overall frame diagram

3.1 实验分析

本实验共采集X/Y/Z轴向的陀螺仪数据15000组，网络迭代次数100次.图7为原始数据和预测数据，图8为X/Y/Z轴不同网络层的损失函数对比.

图7 X,Y,Z三轴原始数据和预测数据Fig.7 X, Y, Z three-axis raw data and predicted data

图8 X,Y,Z不同网络的损失函数对比图Fig.8 Comparison of the loss functions of different networks in X, Y and Z

3.2 实验结果

3.2.1 不同网络对陀螺仪数据补偿的优势

通过对比三种不同的网络层结构，可以看出来LSTM-LSTM在进行网络模型训练中损失函数相比其他两种结构有一定的优势，在训练时间上LSTM-GRU和GRU-LSTM相对于双层LSTM，训练速度更快.这也验证了GRU在细胞结构上是LSTM的一种简单变体，将输入门、输出门、遗忘门转变为重置门和更新门.相对原始数据标准差(STD)经过3种网络训练的标准差，都要优于原始数据的标准差，补偿后的陀螺仪输出更加稳定.

3.2.2 陀螺仪随机误差预测前后对比

在Matlab中，通过Allan方差，然后进行曲线拟合，根据前述的误差分析，可以在Matlab中画出Allan方差双对数曲线，进一步求得随机误差.

由表2和表3可以看出，通过Allan方差得知三种不同算法对随机噪声都有明显降低，但三种方法之间差别微小，一方面验证了网络结构的稳定性，另一方面说明了GRU和LSTM在性能上差别不大，本实验求得陀螺仪的5种随机误差，分析对比发现LSTM-GRU在输出信号降噪效果上优于LSTM-LSTM和GRU-LSTM的降噪效果，最后分析LSTM-GRU网络在原始数据上的降噪效果.实验结果发现X轴陀螺仪量化噪音、角度随机游走、零偏不稳定性、角速度游走、速度斜坡，分别降低了36.6%，21.5%，2.9%，75.9%，93.5%；Y轴陀螺仪降低了14.8%，4.2%，7.16%，66.7%，95%；Z轴陀螺仪降低了34.1%，3.6%，5.8%，80.2%，96.6.从而更加验证了经过循环神经网络训练可以有效的对陀螺仪输出数据进行补偿，并且补偿效果有明显的提高.

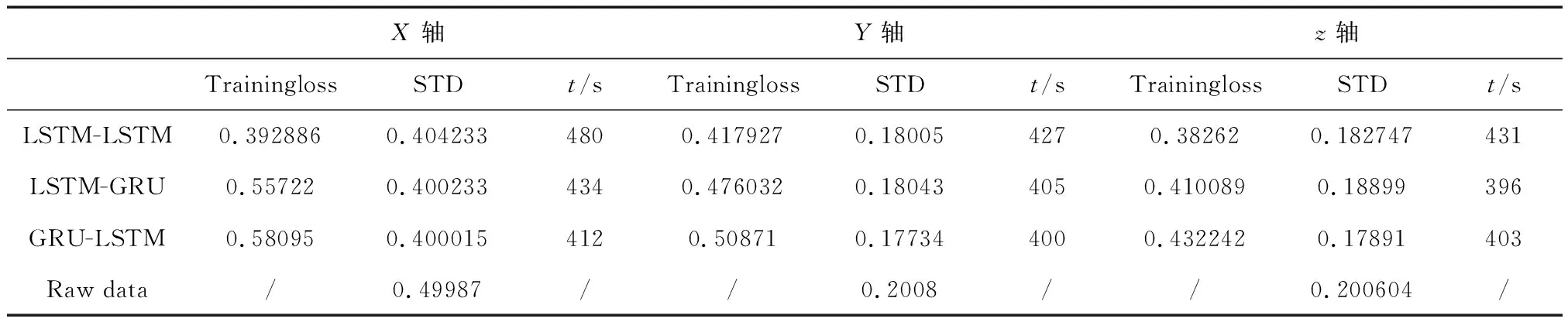
表1 原始数据和3种网络损失值、标准差和耗时Tab.1 Original data and 3 kinds of network loss values, standard deviation and time

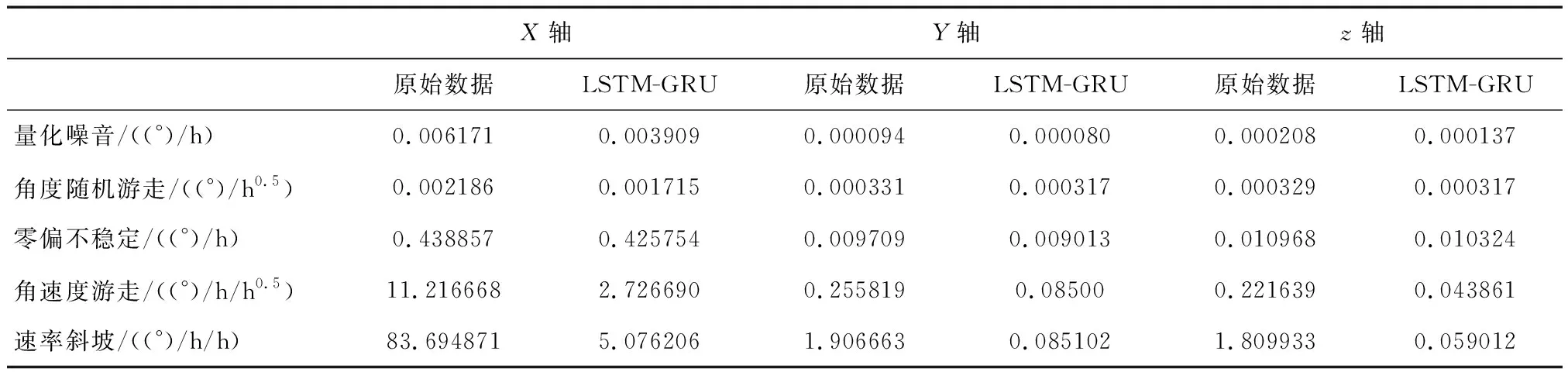
表2 5种随机误差的对比Tab.2 Comparison of 5 random errors

表3 随机误差的对比Tab.3 Comparison of random errors

4 结 论

本文针对传统算法针对陀螺仪精度补偿的不足，提出了一种基于循环神经网络的陀螺仪降噪方法，既克服了传统方法的建模困难，又通过引入长短记忆神经网络和门循环单元克服了传统神经网络的梯度消失和梯度爆炸.基于本实验可以得到的结论如下：

1)本文验证了LSTM在陀螺仪输出补偿上计算速度不如GRU，在性能上比GRU有一定优势.

2)验证了深层次网络能够更好的提取信息特征，更好的加深学习能力，提高泛化能力.

3)LSTM-GRU、GRU-LSTM、LSTM-LSTM不同网络层的结合，实验结果表明LSTM-GRU降噪效果优于GRU-LSTM和LSTM-LSTM.

4)实验结果验证了深度神经网络结合不同层次的网络结构，对陀螺仪数据预测具有较好的效果，扩宽了深度学习的应用领域.