稳态制动点头影响因素分析

2021-01-04闫瑞雷庄毅胜杜锡滔

汽车工程师 2020年12期

闫瑞雷庄毅胜杜锡滔

（广州汽车集团股份有限公司汽车工程研究院）

制动点头性能是汽车操纵稳定性及舒适性的重要评价指标，制动过程中点头角的大小严重影响消费者的驾乘体验[1]，尤其是0.3g～0.6g 常用制动减速度工况下的点头角，因此，研究如何控制制动点头角的大小就变得非常重要[2]；此外，在车型开发初期，往往存在对标数据不全、各系统方案尚未明确、仿真分析缺乏输入等困难，因此，如何根据整车以及制动系统参数匹配悬架系统参数，以达到较好的制动点头性能，始终是悬架设计的难点。文章在考虑整车参数、制动系统以及缓冲块刚度、间隙等悬架系统参数的基础上，通过分析制动过程中整车以及前、后悬架在垂向和纵向的受力特点，建立稳态制动点头角数学计算模型并以某SUV 车型为例，通过对比计算结果与试验结果的差异，验证数学模型的准确性，最后，利用MATLAB 的GUI 功能编制了制动点头角参数化软件并对各影响因素进行量化分析。

1 制动点头角数学模型的建立

1.1 假设条件

由于悬架系统结构及其运动过程的复杂性，为了便于力学分析和计算，对其作如下假设：1）忽略悬架系统本身的物理结构及各部件之间的拓扑关系，仅考虑悬架系统与车身在纵向和垂向的力学特性；2）忽略汽车制动过程中整车参数以及悬架K&C 特性[3]的变化；3）忽略整个制动过程中电控系统，尤其是防抱死制动系统（ABS）和电子制动力分配系统（EBD）的影响。

1.2 整车力学特性分析

汽车制动过程中，由于载荷发生转移使得汽车质心前移，导致前悬架压缩下沉，后悬架拉伸抬起，从而产生制动点头角，本节假设汽车以减速度ax（ax≤0.6g）进行制动，通过对其达到稳态后的受力状态进行分析[4]，得到制动过程中的载荷转移量ΔFz，如图1 所示。

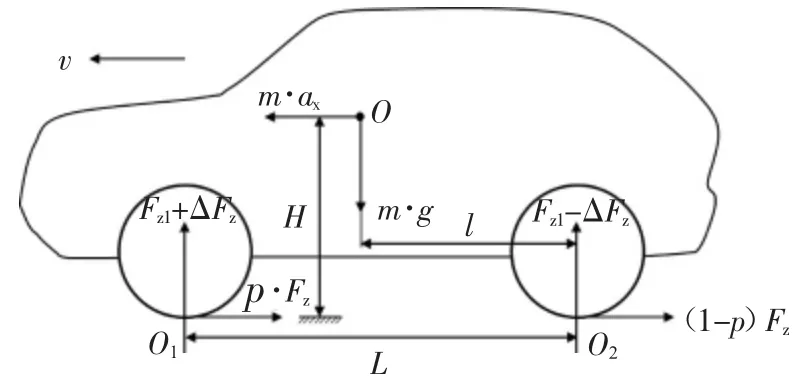
图1 整车力学特性分析示意图

图1 中：v 表示汽车行驶速度；O 表示整车质心位置；O1、O2表示前、后轮胎接地点位置；p 表示前轴制动力分配系数，一般在0.7 左右；Fx表示汽车以减速度ax在制动过程中受到的制动力。根据达朗贝尔原理[5]分别建立汽车在静止以及制动2 种状态下，各力绕后轮接地点O2的力矩平衡方程：

静止状态：

制动状态：

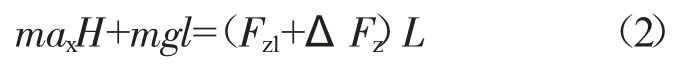
式中：m——整车质量，kg；

g——重力加速度，m/s2；

l——整车质心到后轴的距离，mm；

Fz1——汽车静止状态下的前轴荷，N；

L——轴距，mm；

H——整车质心高度，mm；

ΔFz——载荷转移量，N。

将式（1）代入式（2）并化解即可获取汽车以减速度ax制动过程中的载荷转移量：

1.3 前悬架力学特性分析

汽车制动过程中产生的载荷转移导致前轴荷所增加的ΔFz主要由两部分承担：1）由悬架杆系所提供的抵抗悬架压缩的抗点头力；2）由弹簧、缓冲块以及橡胶衬套等弹性件通过变形所提供的支撑力。两部分力共同支撑前悬架抑制其下沉，如图2 所示。

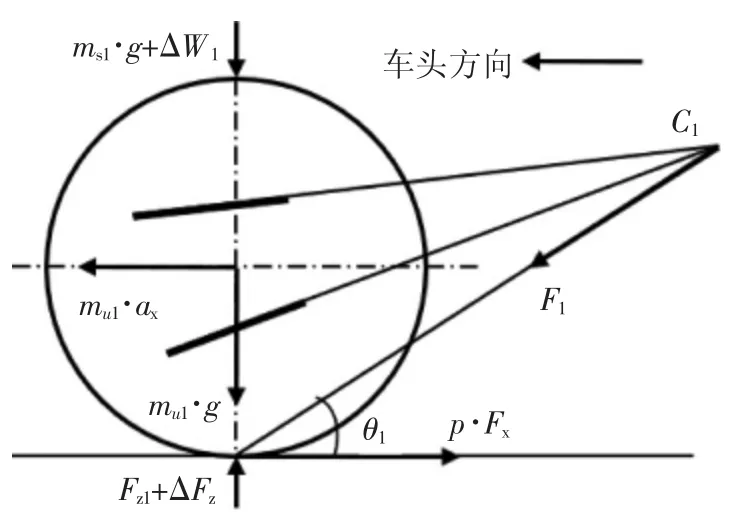
图2 前悬架力学特性分析示意图

图2 中，C1表示前悬纵向摆动虚拟中心，即纵倾中心[6]，通过对前悬进行纵向和垂向受力分析，计算弹性件通过变形对车头所提供的支撑力：

纵向：

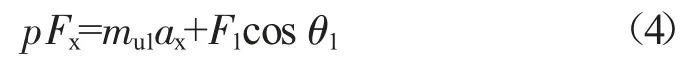
垂向：

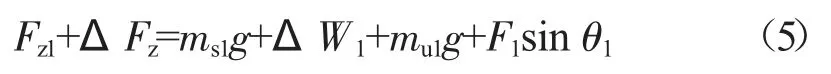
式中：mu1——前轴簧下质量，kg；

F1——前悬杆系支撑力，即抗点头力，N；

θ1——前悬抗点头角，（°）；

ms1——前悬簧上质量，kg；

ΔW1——前悬弹性件支撑力，N。

当汽车处在静止状态时，存在以下力学关系：

联立式（4）、式（5）和式（6）可得到导致前悬在制动过程中产生压缩的力，即弹性件支撑力为：

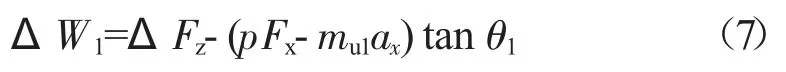
1.4 后悬架力学特性分析

与前悬架类似，汽车制动过程中，后轴所减少的载荷ΔFz同样由两部分承担：1）由悬架杆系所提供的抵抗悬架拉伸的抗举升力；2）由弹簧、缓冲块以及橡胶衬套等弹性件通过变形所提供的变形力。两部分力共同作用于后悬抑制其抬起，如图3 所示。

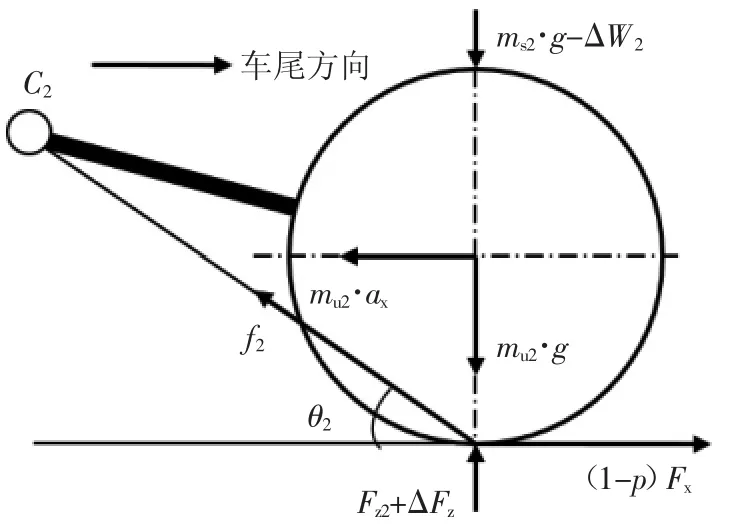
图3 后悬架力学特性分析示意图

图3 中，C2表示后悬纵倾中心[6]，与前悬类似，通过对其进行纵向和垂向受力分析，计算弹性件通过变形所产生的变形力：

纵向：

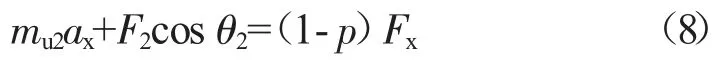
垂向：

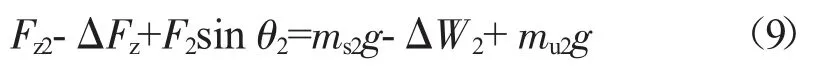
式中：mu2——后轴簧下质量，kg；

F2——后悬抗举升力，N；

θ2——后悬抗举升角，（°）；

ms2——后悬簧上质量，kg；

ΔW2——后悬弹性件变形力，N。

当汽车处于静止状态时，存在以下力学关系：

联立式（8）、式（9）和式（10）可得到导致后悬在制动过程中产生拉伸的力，即弹性件变形力为：

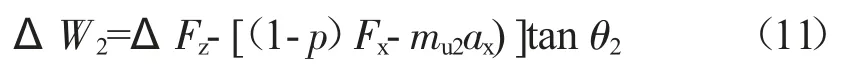
1.5 制动点头角计算

制动点头角是指制动过程中，汽车纵轴线与水平面夹角的变化量，如图4 所示。

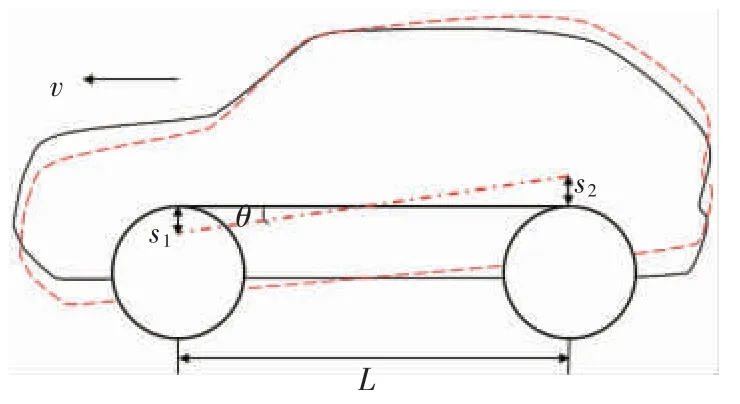
图4 汽车制动点头角计算示意图

假设汽车以减速度ax进行制动，前悬下沉量为s1，后悬抬起量为s2，此刻，制动点头角θ 可表示为：

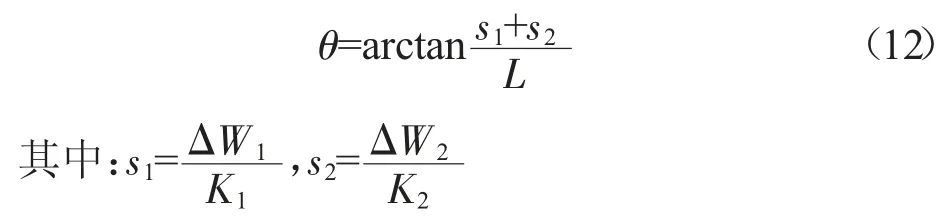
式中：K1，K2——前后轴悬架刚度，N/mm。

前悬架刚度K1需要考虑缓冲块间隙d 以及缓冲块刚度Kb对悬架刚度的非线性影响。

2 数学模型验证及软件编写

以某款SUV 车型为例，分别在汽车前、后端安装高度传感器并利用V-Box 读取减速度信号，根据0.3g、0.6g 制动减速度工况下，前、后高度传感器读取的高度变化量以及两传感器之间的纵向距离来计算制动点头角大小。同时，按照前文所推导的制动点头角数学模型，计算相同工况下的制动点头角并与实测结果进行对比，以验证数学模型的准确性。计算所需的主要参数，如表1 所示。

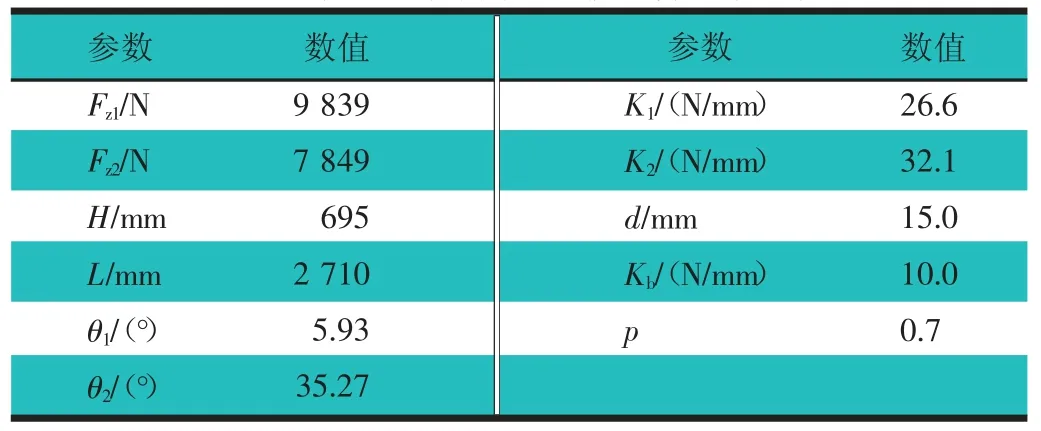
表1 某SUV 转向系统刚度计算基本参数

由于数学模型存在输入参数多、计算过程复杂等问题，导致计算效率低、错误率高，不利于在项目开发中进行实际应用。为了简化数学模型的计算过程、提高其实用性和可视化，利用MATLAB 的GUI 功能编制参数化人机交互工作界面[7]，如图5 所示。

图5 参数化人机交互工作界面示意图

将表1 中所列的参数输入参数化软件，对制动点头角进行计算并与实测结果进行对比分析，如表2 所示。

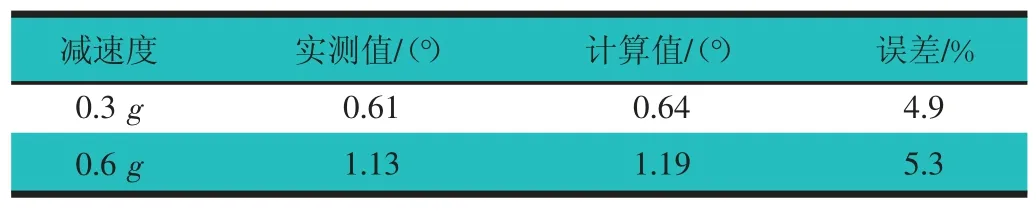
表2 某SUV 制动点头角对比

从表2 可知，0.3g 和0.6g 减速度工况下，制动点头角计算值与实测值误差基本在5%左右。其差异主要是由于在制动过程中，悬架的运动特性和受力特点实时变化，从而导致悬架抗点头（举升）角在制动过程中并不是定值，而在数学模型中为了便于计算，将其简化为固定值；此外，零部件公差、试验操作以及数据处理误差也会造成计算值与实测值的差异。

3 制动点头角影响因素分析

轴荷、质心高度以及轴距等整车参数虽然影响制动点头角的大小，但整车参数的设定往往受市场定位、汽车配置、布置空间以及平台化程度等因素的限制，且整车参数作为项目开发初期最基本的设计参数，不能轻易变更，否则，将严重影响整个项目的开发。因此，本节以0.6g 制动工况为例，重点分析悬架系统以及制动系统参数对稳态制动点头角的影响，并对其影响程度进行量化，其中，悬架系统和制动系统参数的变化量根据经验设定，分析结果如表3 所示。

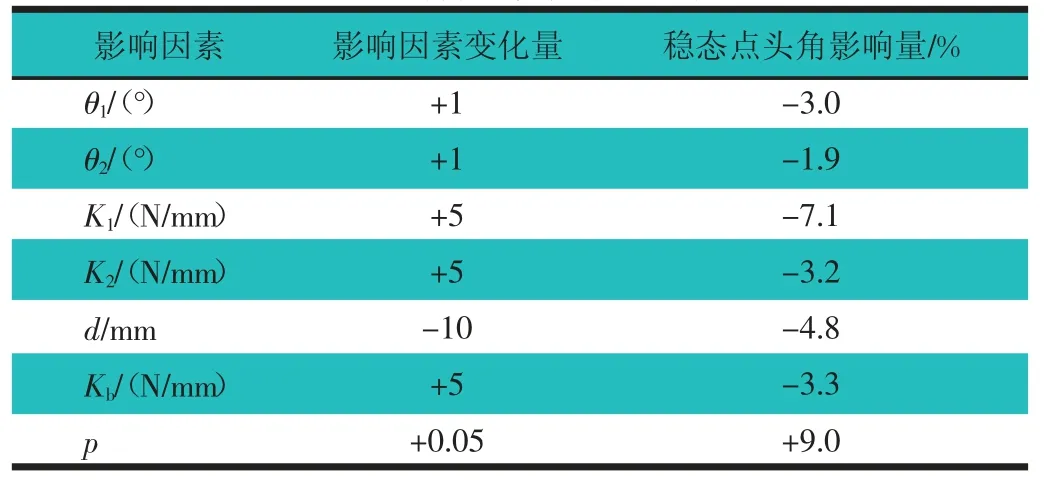
表3 稳态制动点头角影响因素量化

由于不同物理量之间无法采用统一的变化基准，因此，很难基于同一标准衡量各因素对稳态制动点头角影响程度的大小，但根据表3 的计算结果可知：稳态制动点头角与悬架抗点头（举升）角、悬架（缓冲块）刚度等参数呈正相关，与前悬缓冲块间隙以及前轴制动力分配系数呈负相关。此外，基于表3 的分析，可以为底盘研发人员在硬点设计、制动系统匹配[8]以及弹性件设定等方面提供理论参考，以确保制动点头性能达到预期目标。