涌浪条件下的浅海表面声道脉冲声传播∗
2021-01-02彭朝晖胡承昊李整林于梦枭张青青
刘 今 彭朝晖 胡承昊 李整林 于梦枭 张青青
(1中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)
(2中国科学院大学 北京 100049)
(3中国船舶工业系统工程研究院 北京 100094)
0 引言
我国东南沿海大陆坡浅海区域,冬季受强劲北风作用,表层介质混合常形成等温层,从而构成表面声道,有利于声传播,但又因海面的不平整性而存在不利于声传播的一面。海面的不平整性主要因小尺度的海面风浪或降雨以及大尺度的涌浪而产生。为了表述上的简洁,将这两种不平整海面统称为粗糙海面。
关于粗糙海面对声场的影响的研究,国内外学者开展了大量的工作。王先华等[1]对比两次声传播实验数据,发现实验环境均相同,只有海况不同,导致两次实验中声传播损失相差较大,研究了海面波浪起伏对声传播的影响。Liu等[2]分析了随机起伏海面下声传播损失的统计特性,指出传播损失的分布与频率、风速和距离有关。汪洋等[3]指出在浅海负跃层环境中,声源在近海面等温层中时,起伏海面和气泡层对声传播影响较大,声源在远离海面的负跃层梯度环境中时,对声传播的影响较小。Badiey等[4]在对一次实验数据的分析中,指出粗糙海面使得信号波形展宽,相关性下降。以上研究主要针对的是典型的浅海环境下的粗糙海面对声场的影响,未综合考虑表面声道的作用。
尹爽[5]假设了一个浅海200 m厚的表面声道,通过仿真分析指出,声源离海面越近、风速越大,粗糙海面造成的声衰减越多,但是未进行实验验证。Siderius等[6]基于实验数据,分析了浅海环境,存在表面声道时,时变的粗糙海面对声传播损失和时域波形的影响。姚美娟等[7]利用一次深海声传播实验数据,指出了对于中远距离声传播,浅海或者存在表面声道的环境中,粗糙海面对传播损失的影响不可忽视。
上述3个工作主要针对的是浅海或者深海环境,未考虑涌浪海面的作用。而涌浪所造成的粗糙海面会给声场造成更大的衰减。Vadov等[8]基于实测数据对表面声道下的声衰减系数进行分析,发现即使额外考虑上跟海况有关的散射衰减系数,也不足以解释实验中出现的较大衰减。指出在他们下一步工作中,当风速较小时,需要考虑涌浪带来的声衰减。Weston等[9]在一次浅海实验中就涌浪可能会对声压级造成的影响做了简单描述。
在南中国海北部存在海深约300~500 m的大陆坡海区,冬季时,上层水体中经常存在表面声道,下层为一个负跃层剖面,且由于季风影响,经常存在较大涌浪。刘今等[10]在该海区的一次冬季声传播实验中,发现受海面涌浪的影响,表面声道中传播的频率为1000 Hz的脉冲声,其传播损失增长了10 dB。本文在该文工作的基础上,继续对实验数据进行深入分析,研究发现,涌浪海面还会对表面声道以下的时域脉冲波形产生重要影响。爆炸声源产生的单个脉冲(不考虑多次脉动)经多径传播后形成多个脉冲到达,理论分析和实验数据表明,由于涌浪的存在,表面声道以下的水听器接收到的第一个到达的脉冲幅度明显增加。
1 粗糙海面建模
为了分析粗糙海面对声波时域波形的影响,首先需要进行粗糙海面建模。本文中所使用的是风浪叠加涌浪的粗糙海面模型[10],风浪部分采用PM谱结合蒙特卡洛的方法产生。涌浪部分采用正弦波的形式。
首先给出风浪海面的具体实现过程。粗糙海面可以当作是具有随机振幅和相位的谐波叠加而成,假设不考虑时变的一维粗糙海面的长度为L,离散点数为N,则海面上任意一点xn的高度f(xn)可表示为如公式(1)所示[11]:
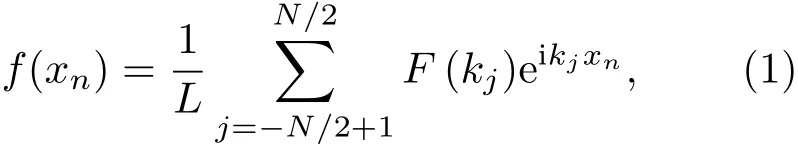
其中,xn=nΔx,n=−N/2+1,···,N/2,kj为离散波数,kj=2πj/L,j=−N/2+1,···,N/2。f(xn)与F(kj)互为傅里叶变换,F(kj)的表达式如公式(2)所示:
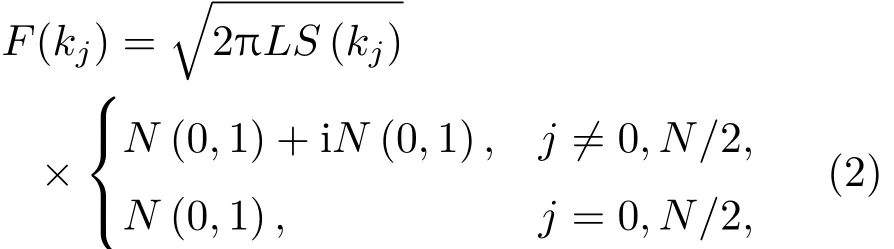
其中,N(0,1)表示均值为0、方差为1的正态分布,F(kj)满足共轭对称的关系,即F(kj)=F(k−j)∗。S(kj)为PM谱的表达式,如公式(3)所示:
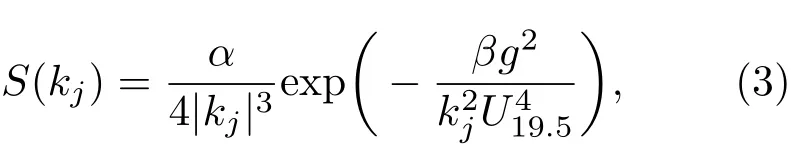
其中,α=8.1×10−3,β=0.74,g表示重力加速度,取9.8 m/s2,U19.5为距海面19.5 m高处的风速,它与10 m高处的风速U10的对应关系为U10/U19.5≈0.94[5]。
船载风速仪实测的海面风速结果显示,在距接收阵1 km以内的平均风速为8.1 m/s,1 km以外的平均风速为3.6 m/s。根据实测风速,利用公式(1)~(3)即可得到风浪海面。
涌浪海面部分可用正弦波表示,表达式如公式 (4)所示[12]:
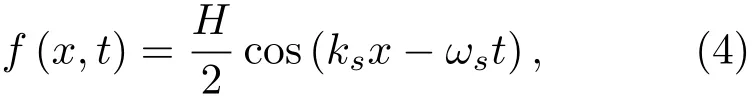
其中,f(x,t)表示海面起伏高度,H为波高,ks为波数,ks=2π/λs,λs为波长,ωs为角频率,t为时间。假设海面不随时间变化,取t=0 s,λs=80 m,H=2.5 m,可以得到涌浪海面。将风浪海面与涌浪海面相加即可得到最终的海面模型,最终得到的混合海面表达式为
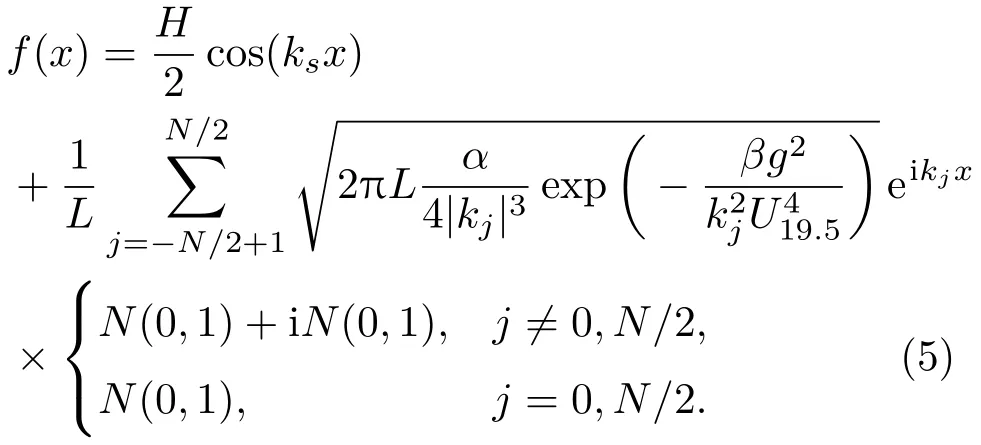
利用公式(5)进行海面建模,结果如图1(a)所示。在文献[10]中指出主要是涌浪海面对声场起的作用,因此在下文中将此叠加后的海面均简称为涌浪海面。图1(b)给出了0.8~1.3 km的海面放大示意图,可以发现1 km外是涌浪海面叠加了较小的风浪起伏,真实感较好。
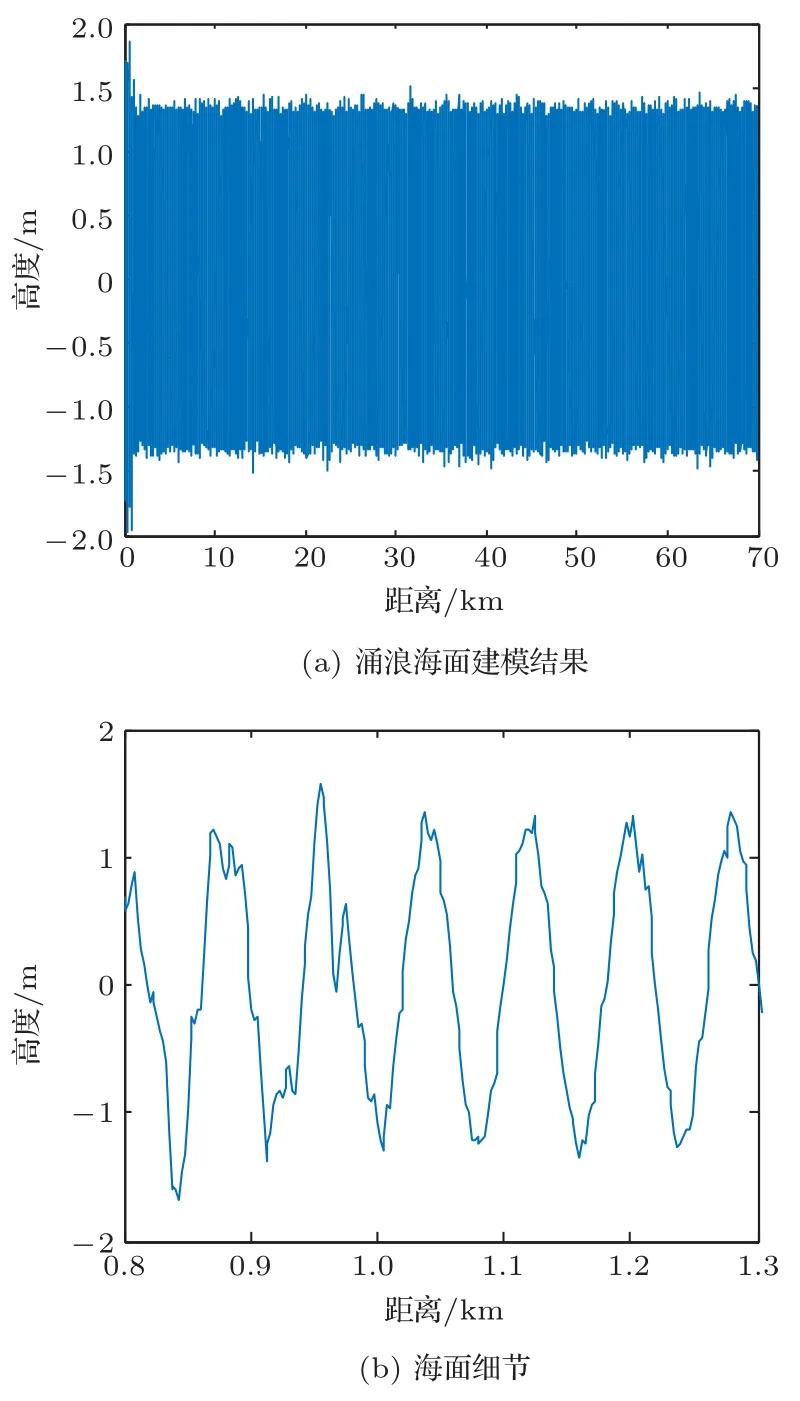
图1 涌浪海面建模结果及海面细节Fig.1 The swell sea surface and sea surface details
考虑到海洋环境的水平变化特性,以及需要粗糙界面作为输入边界的情况,本文采用抛物方程模型Ramsurf计算宽带的频域声压p(r,z,ω)。利用公式(6)将宽带声压进行逆傅里叶则可以得到时域声压p(r,z,t)[13]:
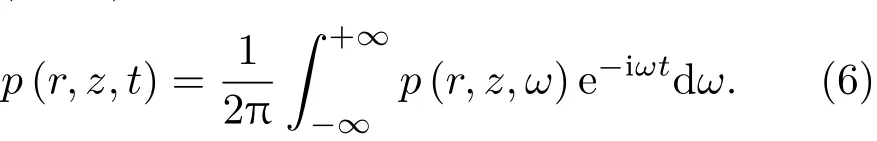
2 实验介绍
2017年,中国科学院声学所声场声信息国家重点实验室的研究人员在南中国海北部陆坡海区进行了一次声传播实验。实验采用如图2(a)所示单船结合垂直阵的方式。垂直阵由自容式水听器和温深传感器组成,水听器深度在25~330 m之间非均匀布放,信号采样率为16 kHz。实验期间,实验1号科考船沿着声传播路径投掷1 kg TNT当量的爆炸声源,爆炸声源标称深度为50 m。声传播路径总长约155 km。在文献[14]中指出,测线位置处的海底底质随空间变化,但由于海底底质的影响不是本文的研究内容,因此在实验和仿真时,取从接收阵出发的70 km以内作为研究区域。图2(b)、图2(c)分别给出了研究区域的实测海深以及声速剖面情况。从图中可以看出研究区域海深在344~430 m之间,并且存在倾斜度较小的斜坡。为了方便后续计算,声速剖面中不足海深处进行了插值处理。图中可以看出,该海区的声速剖面为典型的冬季深海声速剖面。上层由于风浪的搅拌作用,形成等温层,构成表面声道,并且表面声道的厚度较大,且随距离变化,约在74~102 m之间。下层为典型的负跃层声速剖面。
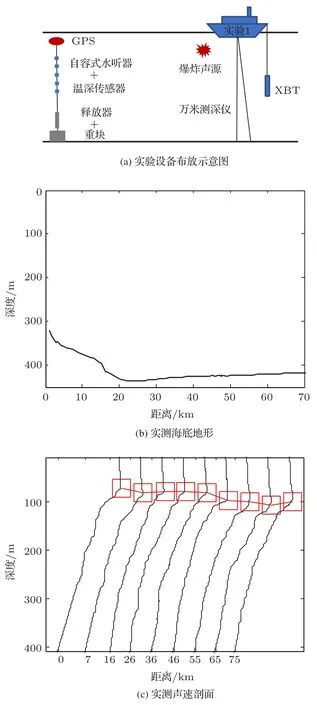
图2 实验设备布放示意图和实际环境测量结果Fig.2 The con figuration of the experiment and measured environmental results
3 实验数据分析
在文献[10]中指出,实验期间,该海域存在较大涌浪,对声源中心频率为1000 Hz、带宽为1/3倍频程的声传播损失数据产生较大的影响。下面就涌浪海面对该频段的时域波形的影响进行探讨。
首先给出该频段下,不同接收距离处时域波形的测量结果,如图3所示。由于在实验期间,受海流的影响,阵型一直在波动(见图4),因此不同距离处的实验信号被同一水听器接收到时,接收深度可能不尽相同。图3中的3张子图存在一个共同点,上面4个水听器(位于表面声道中),第一个脉冲几乎处于同一时间到达,而从第6个水听器开始,收到的第一个脉冲的时间随深度下降而逐渐提前的,均早于表面声道中的第一个脉冲的到达时间。理论上,当声源位于表面声道中时,表面声道中的信号能量会以群速度传播。因此,上面4个水听器应具有相近的到达时间。但是,从图2(c)可以看出,表面声道内的平均声速最高,因此,理论上,处于表面声道内的水听器相较于其他深度的水听器应最先收到信号,而实验结果是下面的水听器先收到信号。经初步分析,这是因为实验期间接收阵发生倾斜,水听器的深度波动较大。
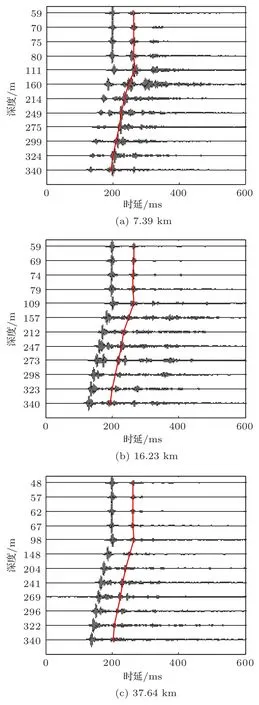
图3 不同距离的波形测量结果Fig.3 Measured signals at different ranges
尽管实验中未测量流向,无法确定阵倾斜的方向,但可以根据垂直阵水听器及温深计的相对位置和温深计测量的深度数据,估计出垂直阵在不同时刻的阵形,如图4所示。假设垂直阵向声传播方向倾斜,从图中可以看出,水听器的偏移距离从上到下是逐渐减少的,不同水听器接收到的信号的声传播路径,从上到下依次变短,因此到达时间也逐渐缩短。上面4个水听器的深度和接收距离均相差较小,并且处于表面声道中,因此几乎同时到达。在后面的仿真分析中,均使用倾斜阵型。

图4 阵型Fig.4 The array geometry
对比图3(a)(b)(c),可以发现不同距离上的接收信号的脉冲幅度存在较大差异。为了便于比较,图中每个深度上的信号均进行了单独归一化。在图3(a)中,上面四个水听器(表面声道内)接收信号的第一个脉冲相对幅度较大,而下面几个水听器(表面声道外)接收信号的第一个脉冲的相对幅度近乎呈现随着深度逐渐减小的趋势。而图3(b)(c)中所示,当距离较大时,每个深度上第一个脉冲的相对幅度几乎均为各自深度上信号幅度的最大值,并且在时间上越靠后的波包的幅度越小。这与近距离的信号幅度随时间变化的形式相差较大。
图3(a)~(c)中,在第一个脉冲波到达后约64 ms的时刻,均存在一个相对较弱的脉冲,在图中用红色实线标出,它与第一个脉冲的时间间隔不随深度变化而变化,为二次脉动信号。在每个距离上,观察上面几个水听器,二次脉动信号旁边均有一个相对较弱的信号,定义为第二个脉冲。其中距离为16.23 km时,二次脉动信号与第二个脉冲信号耦合在一起。对于接收距离分别为7.39 km、16.23 km、37.64 km时,第二个脉冲与第一个脉冲的时延分别为58 ms、64 ms、88 ms。可以发现第二个脉冲到达的时间随着传播距离增加逐渐滞后。
4 涌浪海面下脉冲到达结构分析
在文献[10]中,发现涌浪海面对表面声道内的传播损失有重要影响。下面采用同样的方法,对涌浪海面下的脉冲波形进行理论计算。为了进行对比,同时给出平整海面建模下的波形结果。仿真时,声源中心频率为1000 Hz,将声源分别置于图2(b)中7.39 km、16.23 km、37.64 km处,声源深度为50 m,接收距离位于0 km处。接收深度为实验中,声源在不同距离处投放时所对应的水听器的实际深度。海底参数选择cb=1540 m/s,ρb=1.47 g/cm3,αb=0.45 dB/λ[10]。粗糙界面应用如图1所示的海面。仿真结果如图5所示,图5(a)~(c)为平整海面结果,图5(d)~(f)为涌浪海面结果。
对比图5(a)与图5(d),此时声传播距离较近,可以发现各个深度上第一个脉冲的相对幅度的规律,二者差别不大:表面声道内,第一个脉冲幅度相对较大,表面声道以下,第二个脉冲幅度相对较大,第一个脉冲相对幅度与实验数据一致。最后一个脉冲的波形,明显平整海面下相对清晰,而涌浪海面下,相对幅度较弱,与实验结果更加接近。
对比图5(b)、图5(e)与图5(c)、图5(f),此时声传播距离逐渐增加,可以看出平整海面下第一个脉冲的到达幅度随深度变化的规律和图5(a)类似,随距离变化不大;而粗糙海面下随着距离的增加,第一个脉冲的到达幅度均为各自深度上的最大值,并这一结果与实验数据更相符。此外,平整海面下,300 ms后的脉冲幅度依然很强,而涌浪海面和实验结果显示300 ms后的脉冲幅度较弱。
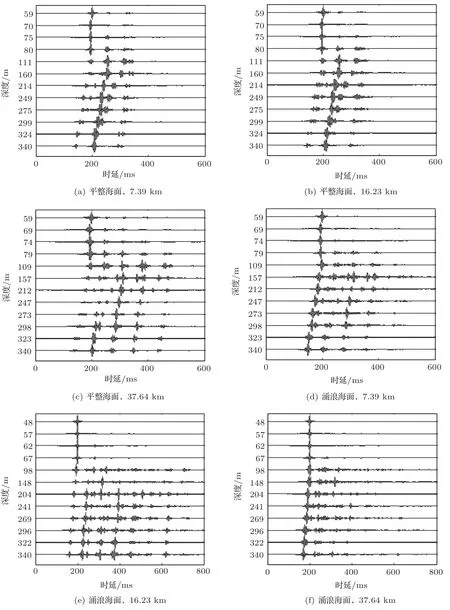
图5 两种海面条件下不同距离的时域波形仿真结果Fig.5 Modeled time domain waves under two sea surfaces at different ranges
关于第一个波和第二个波的时间差,两种海面情况下,理论预报的结果相差不大。3个距离下,时间差依次为55 ms、56 ms、84 ms,大体上也是遵循着随距离增加,时间差逐渐增大的规律,与实验规律相一致。与实验的误差分别为3 ms、8 ms、4 ms,可能的原因,一是海洋环境、海底参数的不确定性;二是在计算实验数据中的时间差时,用的是两个波包的峰值处对应的时延相减得到,对于16.23 km的结果,二次脉动将界面反射信号覆盖了,由此可能使得时延估计不准确。
5 涌浪海面对时域波形影响的理论解释
为了更加清楚地理解涌浪海面对脉冲波形幅度的影响,以距离16.23 km处的仿真环境为例,来详细分析和解释涌浪海面对脉冲波形的影响。仿真时声源中心频率为1000 Hz,带宽为1/3倍频程。
5.1 声传播损失分析
首先从传播损失角度进行考察,计算两种海面条件下全海深的传播损失结果。仿真环境与图5(b)、图5(e)中的仿真环境一致。为了看清涌浪海面对传播损失的影响的细节,取出距离1.6 km、海深100 m以内的结果,如图6所示。图中明显可以看出,涌浪海面使得声场的干涉结构变得复杂,部分声能量相干叠加后,以较大的掠射角朝向海底,这部分能量在远距离传播过程中,一部分返回上层水体中不再离开表面声道,一部分会继续与海面作用,穿透表面声道,使得表面声道以下的声信号的能量增加。
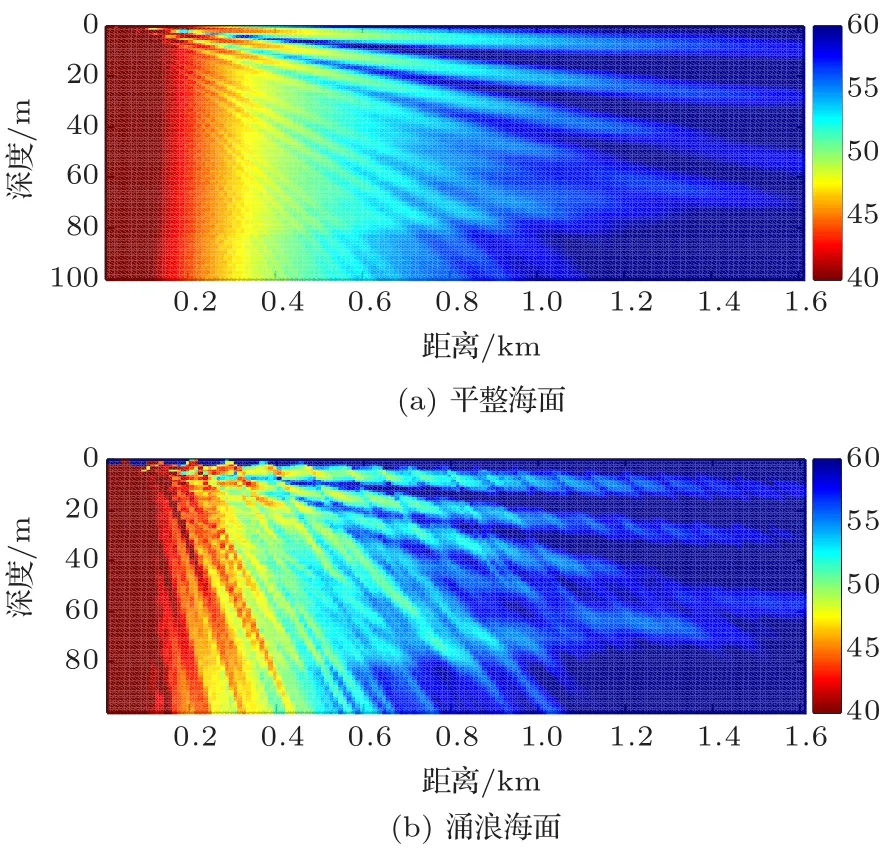
图6 两种海面条件下近距离声传播损失伪彩图Fig.6 The pseudo color map of transmission at short ranges under two surfaces
5.2 声脉冲幅度
涌浪海面使得表面声道以下的信号的第一个到达的相对幅度增强有两种可能的原因:一是与平整海面相比,第一个波的幅度变化不大,而后面的波的幅度大大减小,使得第一个波的幅度相对较大;二是第一个波的绝对幅度的确增加。为了探讨是哪种原因,图7给出了两种海面下,声源距离为16.23 km、接收深度分别为59 m和247 m时的声压计算结果(声压不做归一化处理)。对于59m接收深度处的信号,两种海面下第一个波的信号幅度相差相对较小,但是平整海面下的界面反射的到达信号数量多,并且整体上幅度也较高。而对于247 m处的接收信号,平整海面下第一个波的幅度很弱,其他的反射波的信号幅度较强。而涌浪海面下的结果则刚好相反,第一个波的幅度比其他反射波的幅度高,并且高于平整海面下的第一个波的幅度。这是由于表面声道中的部分声能量经过涌浪海面作用后,穿透表面声道进入下层水体中,使得下层水体中第一个波及其对应的海底反射波的幅度升高。
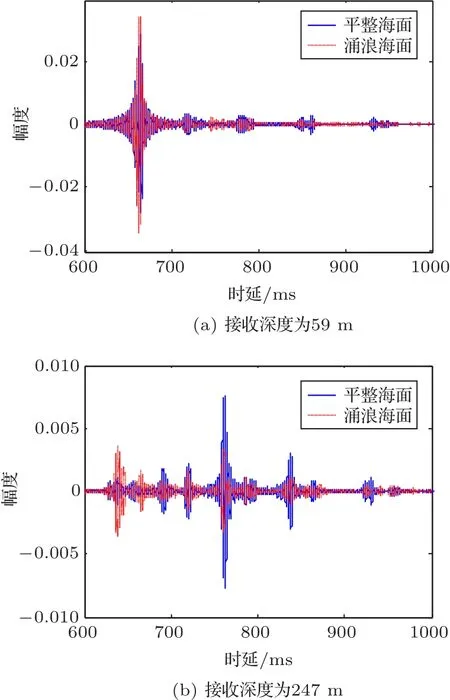
图7 不同深度的水听器在平整海面和涌浪海面下的时域波形对比Fig.7 Comparisons of time domain waves under flat sea surface and swell sea surface at different depths
5.3 声线分析
接下来采用基于射线声学的Bellhop程序计算本征声线,用以分析涌浪海面对表面声道以下的接收器的第一个脉冲的幅度的影响。在Bellhop程序中,当声线与粗糙界面作用时,即使波高较小,但只要波陡足够大,即波面的倾斜度足够大,便能使得声线掠射角大大改变,使得许多声线以较大的掠射角朝向海底。由文献[10]可知,风速较小时,波高较小,对声能量的影响也十分微弱。因此,若想使用Bellhop程序定量考察粗糙海面下的声场是十分困难的,本文仅做定性分析。为了减小运算量,这里做了两点简化,一是粗糙海面舍去了起伏较小的风浪成分,即只保留光滑的涌浪成分;二是波高降为1 m。
在建模时,声源频率为1000 Hz,声速剖面选择实测的随距离变化的声速剖面,地形为实测地形,声源位置在图2(b)中所示的16.23 km,深度为50 m,接收位置在图2(b)中所示的0 km处,接收深度为247 m,海底参数与图5(b)、图5(e)所用参数相同。在实际计算中,将声源置于0 km处,接收置于16.23 km处,相应的地形和声速剖面也均需反转。掠射角范围选择−5°~5°,共1001条声线。计算平整海面和涌浪海面下的本征声线情况,结果如图8所示。图中红色、蓝色、浅青色、黄色、紫色声线分别代表与海底作用1次、2次、3次、4次、5次的声线。将与海底作用1次的红色声线加粗表示。图8(a)中存在一条红色声线,是由于表面声道厚度变浅,导致声线从表面声道中折射下来,到达深水的接收器。图8(b)中,存在两条与海底作用一次的声线到达接收器,其中一条在与海面、海底各作用一次后回到表面声道继续传播,而在第4次与海面作用后,再次反射进入下层水体,到达接收器。另一条红色声线在与海面作用3次后,反射到下层水体中,与海底再作用一次到达接收器。因此可以发现,平整海面建模下,下层水体中能收到的一次海底反射的信号是靠海洋环境的不均匀性(等温层厚度随距离改变)折射下来,声线数量较少。而涌浪海面条件下,声线与任意位置的海面作用后存在一定概率会以较大掠射角反射,穿透表面声道,使得一次海底反射声线的数量相对较多。
这两幅图中的红色声线均对应着时域波形中的第一个到达,由此也就解释了涌浪海面下,下层水听器的第一个到达的幅度比平整海面的大。此外,大掠射角的声线与海底作用次数多,组成了在时间上比较靠后的脉冲到达。涌浪海面使得大掠射角的声线以更加垂直的角度入射到海底,返回水体中的能量减少,因此后面到达的几组脉冲的幅度大大减弱。
6 结论
本文采用理论和实验分析了南中国海北部陆坡海区冬季存在表面声道时的脉冲声传播特性,结果表明,在本文300~400 m左右的海深条件下,平整海面下,声源在表面声道内时,较高频率的声信号主要在表面声道内传播,下层水听器接收到的信号主要由海面海底反射信号以及由于海洋环境的不均匀性(等温层厚度随距离变化),从表面声道中折射下来的信号组成。后者由于在表面声道中传播了较长距离,因此最先到达接收器,但是能量相对较弱。当存在较大涌浪时,形成的粗糙海面可以使得原本在表面声道中传播的信号反射到下层水体中,使得下层水体中的最先到达的信号的幅度增加。同时由于粗糙海面使得大掠射角的声线的反射次数增加,导致后面到达的信号的幅度大大减弱。
本文涌浪模型取正弦波形,假设海面不随时间变化,理论分析、计算其对表面声道脉冲传播的影响。当涌浪海面为时间上随机变化的粗糙海面时,需另行研究。
致谢感谢参加2017年南中国海冬季调查实验的实验1号船上的全体人员,他们的辛勤工作为本文提供了可靠宝贵的数据支持。
