一种用于中医四诊分析的子空间聚类方法

许立辉，陈 敏，王池社

(1.常州市中医医院,江苏 常州 213003； 2.金陵科技学院网络与通信工程学院,江苏 南京 211169；3.安徽理工大学计算机科学与工程学院,安徽 淮南 232001)

0 引 言

中医的证候分类研究是中医辨证施治的核心，具有重要的研究价值和临床应用意义[1]。一般来说，中医的证候分类研究是基于中医的四诊信息开展的。研究通常将常用的各类临床症状分成望、闻、问、切4类标准四诊信息库，再对采集到的病例样本按四诊信息进行量化处理后，采用不同的计算机方法进行证候提取与分析，从而为各类临床病例提供辅助诊疗。

目前有很多机器学习方法应用于中医的证候分类研究[2]。聚类作为一种重要的无监督学习方法，它可以有效分析数据中隐藏的类簇信息，也被广泛应用于中医的证候分类研究[3]。但是，传统的聚类方法在高维数据集上进行聚类分析时，其距离计算由于样本数据分布的稀疏性而无法基于距离来构建簇。中医证候分类研究中四诊量化数据维度由几十维到几百维不等，对于这些高维数据的聚类分析无法实现有效挖掘。本文在对比各类聚类方法的基础上，结合中医证候分类研究的四诊数据集高维的特点，基于子空间聚类CLIQUE算法提出了限定空间搜索策略的改进CLIQUE算法(ChM-CLIQUE)，实验结果表明了本文方法的有效性。

1 子空间聚类

子空间聚类[4]是聚类算法中的一种，它通过特征选择在不同子空间数据集中进行聚类。其算法的核心是将搜索在子空间特征维度中进行，它可以有效地降低待处理数据的维度而提高聚类的效果，已经被广泛应用于高维数据的聚类信息挖掘，如图像处理、人脸识别等领域。

针对子空间聚类本身存在的特点，很多研究者提出了提高聚类性能的算法。将子空间聚类方法应用于多聚类问题[5]，可以有效提升高维数据的聚类性能；Geng等人[6]针对分布式聚类问题中的高维数据在聚类过程中形成的维度灾难问题，提出了一种新的局部密度子空间分布式聚类算法；Zhong等人[7]基于图的子空间聚类方法，提出了一种改进的自适应亲和度矩阵(affinity matrix)方法提高聚类性能；Lakshmi等人[8]提出了一种基于兴趣的子空间聚类算法，他们采用粗糙集理论中的属性依赖来度量子空间，有效解决了子空间聚类的规模随着维度的增长而呈指数级扩展问题；Xue等人[9]基于低秩核方法，提出了一种基于非凸低秩逼近和自适应核的子空间聚类方法，有效解决了数据中的奇异值问题。Wang等人[10]提出了一种快速自适应K均值型子空间聚类模型，从而适用于不同分布下的数据集聚类。

子空间聚类的应用研究方面，Liu等人[11]将子空间聚类应用于信用风险评估，有效解决了信用数据集高维、类别不平衡问题；Guo等人[12]将子空间聚类应用于癌症的亚型识别取得了较好的结果；Zhou等人[13]提出了一种基于稀疏子空间聚类算法的社区检测新方法，以解决在线社交网络中稀疏性和短文本的高维性问题；Zhang等人[14]采用稀疏子空间聚类算法进行出租车运营模式发现；Abdolali等人[15]采用子空间聚类算法有效处理图像数据中的去噪问题。

2 ChM-CLIQUE方法

2.1 CLIQUE算法

CLIQUE算法是一种经典的基于网格的子空间聚类算法[16]，主要用于发现子空间中基于密度的簇。经典的CLIQUE聚类算法过程如下：

1)将m维数据集划分为互不相交的网格单元gij，这里面的网格单元如定义1描述。

定义1网格单元。令DS={D1,D2,…,Dm}表示m维数据集，每一个互不相交的子空间数据集记为gij(其中i表示第i个子空间，j表示该子空间的第j维元素)，称之为网格单元。

2)计算每个网格单元的密度，网格密度如定义2。

定义2网格密度。对于每个网格单元gij,令投影到该网格单元中数据点的个数为该网格单元的密度，用dij表示网格单元gij的密度值。

3)根据设定的密度阈值来筛选稠密单元。筛选的策略是从任意稠密单元开始，根据深度优先搜索策略来聚集邻接的稠密单元来生成聚类簇。当所有稠密单元都被遍历时，算法终止。稠密单元如定义3。

定义3稠密单元。根据预先设置的密度阈值参数ε，若网格密度dij>ε,则判定网格单元gij为稠密单元，反之gij为非稠密单元。

2.2 基于限定空间的搜索策略

经典的CLIQUE算法，其搜索稠密单元的策略为基于任意发现的第一个稠密单元进行深度优先搜索，搜索过程具有盲目性，算法时间复杂度高；其密度阈值和网格步长为预先设定，对于聚类簇的边界网格单元识别精度较低[17]。

针对上述问题，本文提出了基于限定空间的搜索策略方法进行算法性能改进。方法主要包括2个部分的内容：1)将搜索策略调整为以稠密单元中网格密度最大的单元为中心进行深度优先搜索生成聚类簇；2)基于聚类簇中样本高斯分布的特性[18]引入网格自适应密度这一概念，通过网格自适应密度计算来增强聚类边界的识别精度。

方法中，选择深度优先搜索的起点为稠密单元中网格密度最大的单元，本文定义其为稠密中心网格如定义4。

定义4稠密中心网格。第i维稠密单元的稠密中心网格记为gic：

gic={gik|gik=max(dij)}

其中gik为第i维网格密度最大的稠密单元。

一般来说，对于聚类效果较好的聚类分布，每个簇中的样本点密集地分布在簇中心，而边缘一般比较稀疏[19]，这一特性符合高斯分布的特性。本文通过引入网格自适应密度计算代替密度阈值和网格步长的预先设定方法，增强聚类边界的识别精度。

网格自适应密度计算公式见定义5。

定义5网格自适应密度。定义ρij为自适应因子优化之后网格单元gij的密度，称之为网格自适应密度：

其中：

λij定义为网格单元密度自适应因子，计算如下：

f(dij)为网格单元gij中的概率密度函数，其计算公式如定义6；n为网格单元数。

定义6概率密度函数。定义f(x)为样本点x的概率密度函数如下：

其中：μ为均值，σ为标准差，σ2为方差。

根据上述定义的网格自适应密度值，按下式判别稠密单元和非稠密单元：

2.3 ChM-CLIQUE算法描述

ChM-CLIQUE算法以CLIQUE算法为基础，通过搜索策略的优化提升算法的效率。算法流程描述如下：

1)将m维数据集划分为互不相交的网格单元gij，生成网格单元。

2)计算每个网格单元的密度dij并进行降序排序，记下稠密中心网格gic。

3)通过计算网格自适应密度来识别是否为稠密单元格，并且从每一维度的网格单元密度最大的中心稠密单元开始深度优先遍历生成聚类簇。

经典的CLIQUE算法在识别稠密网格单元时，忽视了样本分布的特性，将聚类边界的非稠密单元中的数据点作为噪点进行处理，导致聚类的精度低。本文引进网格单元的自适应密度ρij，可以有效地解决将聚类边界误判为噪点的问题，从而提高聚类的效率。ChM-CLIQUE算法伪代码见算法1。

算法1ChM-CLIQUE算法

输入：DS，step，ε

输出：ChM-CLIQUE算法结果clusters

1.grid=createGrid(DS,step);

//根据DS生成网格单元

2.grid_den=calDensity(grid);//计算网格密度

3.grid_sort=sortByDensity(grid_den);

//根据网格单元密度进行降序排序

4.create clusters and set clusterNo=0;

//生成聚类簇结果集合

5.for i=1 to grid_sort.length:

6.clusterNo++;

//标记新簇

7.if(grid_sort[i]=0) then

//判断grid_sort[i]是否被“访问”，0为“未访问”

8.if(dense(grid_sort[i])>ε) then

//判断grid_sort[i]是否为稠密单元

9.cluster.add(grid_sort[i]);//将稠密单元加入当前聚类集合中

10.dfsSearching grid_sort[i];//从grid_sort[i]继续dfs遍历

11.end if

12.grid_sort[i]=1;//标记grid_sort[i]为“已访问”

13.end if

14.clusters.add(cluster);//将当前簇加入聚类簇结果集合

15.end for

16.return clusers;//返回聚类的结果集合

3 实验结果及分析

为了检验ChM-CLIQUE算法的聚类效果，本文在中医临床采集数据集上进行多组对比实验。实验所采用计算机的硬件为Intel(R) Core(TM) i5-5200U CPU @ 2.20 GHz，内存8 GB，操作系统为Windows 10 64位操作系统，算法实现采用Python语言。

为了评估聚类算法的有效性，聚类结果的性能评价指标采用轮廓系数(Silhouette Coefficient)[20]，轮廓系数结合内聚度和分离度2种因素，轮廓系数取值范围为[-1,1]，取值越接近1则说明聚类性能越好，相反，取值越接近-1则说明聚类性能越差。

3.1 数据准备

本次应用实验，采用临床采集的患者四诊变量的数据集(简称数据集DM)。数据集DM包含82个样本，每个样本包含1280个特征。82个样本为中医领域的四诊变量，1280个特征为1280个患者在这82个四诊变量上的程度取值情况，通过聚类分析来挖掘这82个四诊变量内部的关联性。而对于数据集DM这种82个样本、1280维特征的数据集，存在“维度灾难”[21]的问题，基本不可能在1280维上产生有效的聚类结果，高维数据可采用降维方法如主成分分析(PCA)[22]，但会导致数据信息丢失，无法形成有效聚类，故采用改进的子空间聚类算法ChM-CLIQUE算法进行聚类。

数据集DM格式如表1所示，四诊变量为样本，共计82个，四诊程度为四诊变量所对应的特征，共计1280个特征，每个特征取值为1、2、3、4，代表无、轻、中、重4个等级，DM数据集如表1所示。

表1 DM数据集的数据结构内容

3.2 聚类结果分析

在数据集DM上进行2组对比分析实验,其中第一组对比分析实验采用了传统的CLIQUE算法,第二组实验采用了改进的ChM-CLIQUE算法，因为CLIQUE算法对于密度阈值和网格步长参数比较敏感，所以对于每组实验分别进行多次实验。结果如表2所示。

表2 2组实验的聚类结果分析表

对于ChM-CLIQUE算法，优化了搜索策略，并且增强了聚类边界的精度，可以从表2看到ChM-CLIQUE算法实验的轮廓系数要高于CLIQUE算法的，并且耗时要更短。不同实验下的轮廓系数如图1所示。

图1 各实验轮廓系数比较

不同实验下，CLIQUE算法实验与ChM_CLIQUE算法实验耗时如图2所示。

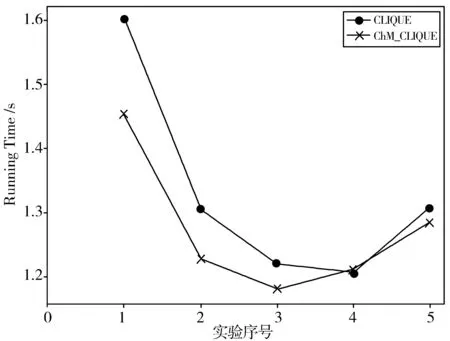
图2 各实验耗时比较

为了检验2种算法在不同规模的数据集的实际运行时间，对数据集DM进行数据增强操作，构造出不同规模的数据集，原始的数据集DM包含82个示例，通过数据增强分别构造出1000、2000、3000、4000、5000样本量的数据集，让CLIQUE和ChM-CLIQUE分别在这些数据集上进行对比实验，比较实际运行时间。不同数据规模情况下，CLIQUE算法实验与ChM_CLIQUE算法实验耗时如图3所示。

图3 2种算法在不同规模数据集上的运行时间

在数据集DM上进行2组对比实验和不同规模数据集实验中可以看出，ChM-CLIQUE算法相对于CLIQUE算法在效率和精确度上都有了一定的提高。

其次使用专家知识作为外部指标[23]来对比CLIQUE和ChM-CLIQUE算法在数据集DM上聚类的结果。根据CLIQUE算法聚类出的结果如表3所示，根据ChM-CLIQUE算法聚类出的结果如表4所示。

表3 CLIQUE算法聚类结果

表4 ChM-CLIQUE算法聚类结果

从中医专家知识的角度出发，对于CLIQUE算法和ChM-CLIQUE算法在临床采集患者四诊变量的数据集上面进行聚类，ChM-CLIQUE算法聚类的结果更加贴近实际，也较为符合中医领域专家的划分规则。

4 结束语

基于限定空间搜索策略的ChM-CLIQUE算法针对传统CLIQUE算法存在的搜索稠密网格单元效率低，以及对于聚类的边界网格单元识别精度低的问题进行优化。ChM-CLIQUE算法对每一维的稠密单元的网格密度进行排序，确定每一维中网格密度最大的稠密单元，以此稠密单元为中心网格进行深度优先搜索生成聚类簇，避免CLIQUE算法“盲目”搜索，提高了算法的性能；对于识别聚类的边界网格单元，ChM-CLIQUE算法基于聚类簇中样本高斯分布的特性提出网格自适应密度，增强聚类边界的识别精度。本文通过多组算法实验和应用实验，分析ChM-CLIQUE算法与传统的CLIQUE算法的时间复杂度和聚类的效果，算法实验采用轮廓系数作为聚类的性能评价指标，表明ChM-CLIQUE算法相比于CLIQUE算法在时间复杂度和聚类效果上都有较为明显的改善。