LC-Raft：一种基于历史日志计算值的一致性算法

马博韬，倪 宏，朱小勇

(1.中国科学院声学研究所国家网络新媒体工程技术研究中心,北京 100190; 2.中国科学院大学,北京 100049)

0 引 言

作为一种易于理解的一致性协议，Raft算法于2013年由斯坦福大学的Diego Ongaro等在其论文《In Search of an Understandable Consensus Algorithm》[1]中首次提出。文中表示，由于现有的Paxos一致性协议实现机制复杂，原理晦涩[2]，需要设计一个足够详细并且易于实现的类似Paxos协议，以方便开发人员能在短期内实现一套可用系统。

基于Raft一致性算法在设计之初便以易于实现、原理清晰等特点作为设计原则，短短几年时间便已被广泛应用于各类分布式环境中。同时，作为Paxos协议的简化版本，Raft算法牺牲了部分性能[3]，对于不同场景中的实际应用，可根据场景特殊性对该算法作出某些方面的具体改进。当分布式系统中的管理节点因故障无法处理集群服务时，需要进行管理节点的重新选举，以恢复系统运作。

在类似于边缘计算的场景中，由于终端设备的不稳定性，设备故障率相比于云端服务器故障率大幅提高，管理节点因故障发生重新选举的可能性也将因此增加[4]。当边缘计算业务需要长时间工作时，不可避免会在工作周期内因设备故障发生多次管理节点选举。

Raft算法在设计选举机制时，选择在每个节点上设置随机起始时间，以尽可能避免出现多个节点同时发起广播竞选。然而，由于竞选信息在分布式环境传输过程中存在通信开销，在此过程中可能存在其余从属节点发起竞选。此时若采用Raft一致性算法进行选举操作，将可能出现因备选节点选票瓜分而导致的多次超时选举，影响分布式系统的可用性。优化Raft一致性算法的选举过程，意义在于减少选举过程平均时间，降低出现选票瓜分导致超时选举的可能性，避免出现多次超时选举的极端情况，从而增加分布式系统的可用性。

本文设计的LC-Raft(Log_Calculation-Raft)一致性算法在原Raft算法基础上，改进原有选举机制，在分布式系统中参与选举所有节点之间的网络通信无故障情况下，能够实现在最长一次超时时间内选举出新的管理节点，且管理节点具有更强的稳定性。本文通过在选举过程中增加基于历史日志计算值的数值指标，评价各个节点的稳定性程度，以获得具有更佳稳定性的新管理节点(Leader)；同时，基于历史日志计算值，修改选举过程整体流程，避免出现多个Candidate节点瓜分选票，实现在一次计时器时间内选举出新的管理节点，增加系统可用性。在实验验证环节，通过Docker容器引擎方案，实现在一台服务器上快速模拟出各种节点规模的实验环境。在此基础上，通过多次实验验证各种节点规模的选举过程，根据统计值验证分析LC-Raft一致性算法与原Raft一致性算法在选举阶段的耗时指标。

1 改进的LC-Raft一致性算法

1.1 适用条件

作为一种能在一次超时时间内完成选举的改良方案，LC-Raft一致性方案需要保证分布式系统中各节点网络通信无故障。当出现网络分区(Network Partition)的情况时，小概率存在多个备选节点处于不同分区中的极端情况。在此情况下，此方案并不能实现分布式的可用性[5]。

1.2 节点状态分析

与Raft一致性算法类似，LC-Raft一致性算法将节点状态区分为3种状态，分别为管理节点(Leader)、从属节点(Follower)以及备选节点(Candidate)[6]。在分布式系统正常工作时，仅存在一个管理节点以及多个从属节点，不存在备选节点，客户端通过与管理节点通信进行相应的幂等操作。每个节点设置有固定的计时器时间，用于区分每个节点是否超时，当从属节点超过计时器时间未接收到来自管理节点的心跳信息时，则该从属节点认定管理节点出现故障，将宣布成为备选节点，通过增加任期，向其余节点广播竞选信息RequestVote RPC，从而得到其余节点的回复信息，当在计时器时间内接收到半数以上节点同意竞选请求的回复时，备选节点将修改节点状态为管理节点，成功竞选。

与Raft算法不同之处在于，备选节点在超过计时器时间后，不再继续保留备选节点状态，转而修改为管理节点状态，具体原因将在下文说明。与此同时，备选节点发现存在任期更大的节点时，将会放弃竞选，恢复为从属节点，并更新任期值为对方任期值。并且，当管理节点发现存在更大任期值的节点时，将会放弃管理节点状态，修改任期，变更为从属节点。发生此状态的原因一般存在2种：一种为管理节点长时间网络故障，未与其余工作节点发生有效通信，其余节点因此已通过重新选举重新构建新的分布式系统，此时管理节点排除网络故障，重新加入该分布式环境，因此需要重新变更为从属节点；另一种情况为管理节点发送的心跳信息过大，并且心跳信息与超时时间比例不合理，从属节点在未完全处理心跳信息时便已达到超时时间，发起管理节点竞选。为了避免上述情况，应合理预设心跳时间间隔与计时器时间之间的比例关系，一般而言，应满足心跳时间<<计时器时间[7]。图1为LC-Raft算法状态转移图。

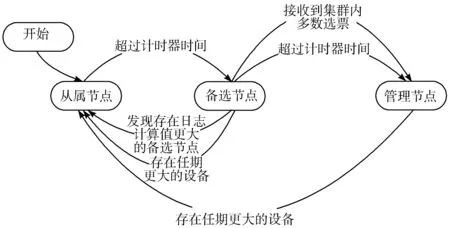
图1 LC-Raft算法状态转移图

1.3 记录节点物理时间日志

在Raft算法的设计机制中，并不考虑物理时间日志在竞选管理节点的选举阶段及状态机修改阶段中的应用，而是采用任期及索引作为逻辑时间加以判断，这是由于各节点物理时间并不能达成完全一致[8]。在使用Raft一致性协议的分布式系统中，已达成一致性的日志项将由管理节点分发至每个从属节点，并保存在日志列表中。日志项对应的任期值不能进行删减，只能增加对应同一任期值更大索引号的日志项或者更大任期值的日志项。因此，日志列表中保存的各日志项表示该节点在分布式环境中运行期间的各类操作，由客户端通过各任期内管理节点将已达成共识的日志项通过AppendEntries RPC消息传递给各个从属节点[8]，从而实现分布式系统中各个节点的最终一致性。

然而，上述日志列表中的日志项只包含有各日志的逻辑时间戳与状态机对应状态值，并不能体现每个节点的稳定性程度。对于稳定性较差的节点，日志项参数并不会告知其余节点其经历的正常工作时间与异常响应次数，在该节点故障排除后，通过与管理节点的心跳信息多次交互后，仍然能表现出与正常节点相同的日志列表与状态机状态。Raft算法中，在节点进行管理节点选举时，具有相同任期的不同备选节点根据其余节点的赞成投票次数来决定最后的管理节点，不仅可能出现因选票瓜分而导致的超时选举，同时也可能出现选举出的新管理节点在稳定性程度上不能胜任工作的情况[9]。

因此，在原有选举机制上，可以考虑加入基于节点历史日志判断稳定性的方案，进行备选节点的二次判决。一方面可以避免多个备选节点瓜分选票导致选举超时，另一方面也可排除所有稳定性较差的备选节点，增强分布式系统的鲁棒性。

1.4 历史日志计算值

本节在原有Raft一致性算法的选举机制上，增加每个节点在固定物理时间范围的异常日志统计，通过事件ID统计在此时段内的典型异常响应次数，以及节点正常工作时间等参数，作为选举管理节点的附加评价指标。从设计目的出发，主要存在2个考量因素：

1)避免出现管理节点选举阶段多个备选节点瓜分选票，造成超时选举。

2)确保新选举出的管理节点是所有备选节点中稳定性最好的节点设备，减少新的分布式系统管理节点发生故障概率。

对于在分布式系统中稳定运行时间更长的节点，倾向于认为该节点状态更加稳定，出现故障或下线的概率更低。尤其在本文需要考虑的边缘计算场景，各终端设备的稳定性远不如云端服务器，在节点可用闲置资源量相差不大的情况下，管理节点的稳定性往往需要作为选举阶段的重要参考指标。

在实施方案中，本节对位于分布式系统中的各个节点定时设置统一物理时间戳，用于计算最近2次物理时间戳之间的固定物理时间。对于每个节点在该时段内日志的异常响应事件ID进行次数统计，在此基础上，2次异常事件ID之间的正常运行时间同样也纳入评价指标。异常事件ID以黑名单方式存储，对应的所有异常事件都有相应的恢复事件ID号，根据具体实验需求，添加需要加入的具体事件ID号。从属节点在超时时间内仍未接收到来自管理节点的心跳信息时，会将上述固定时段内统计的日志信息按照公式(1)计算，并保存为历史日志计算值。

(1)

其中，T表示2次物理时间戳之间的固定时间，M表示统计的异常事件总次数，K表示节点在该历史时段内的正常工作次数，ti表示节点每次正常工作的时间。计算所得值Log_Calculate作为评价节点稳定性的数值指标，介于[0,M]之间，数值越小，表示该节点在此时段内的稳定性越好，以无符号浮点数格式保存。

在从属节点修改为备选节点后，需要将竞选信息RequestVote RPC通过广播发送至其余所有节点，上述计算的历史日志计算值也将包含在其中，新的RequestVote RPC如表1所示。

表1 LC-Raft竞选信息参数表

举例说明，当竞选管理节点的选举阶段存在2个备选节点时，对于上述方案设置2次物理时间戳之间的固定时间为24 h，即8.64×107ms，节点A在此时间内存在异常响应28次，正常运行时间为7.59×107ms；节点B存在异常响应19次，正常运行时间为5.41×107ms。根据公式(1)计算可知，Log_CalculateA≈3.40, Log_CalculateB≈7.10，节点A的历史日志计算值小于节点B，由此判断节点A稳定性更优于节点B。

1.5 选票瓜分解决方案

在原Raft算法中，每个从属节点在回复心跳信息之后，会重置计时器时间，并随机增加一段随机时间，以避免多个从属节点在未收到心跳信息时而达到超时时间[10]。当第一个从属节点在超时时间未收到心跳信息时，将修改节点状态为备选节点，增加任期，并广播竞选信息RequestVote RPC。然而，由于节点之间存在通信开销，存在一定概率使得另外的从属节点在未收到上述竞选信息时也达到超时时间[11]。当上述情况出现时，每个备选节点临近的从属节点将会优先接收到来自此备选节点的竞选信息，从而在分布式系统中形成多个选票分区。Raft一致性算法规定，从属节点只有收到超过半数以上节点的同意竞选回复后才能成为新的管理节点，如果多个选票分区中所有分区均无法达到半数以上选票，则此次管理节点选举失败，所有节点将等待至超时时间后重新竞选。

上述方案在极端情况下将出现多次超时选举，尽管出现概率较小，但在终端资源池中，由于设备的不稳定性，频繁的重新选举过程仍然需要从实现机制上避免上述情况发生[12]。在本节提出的方案中，分布式系统中的各个节点仍然设置有固定的计时器时间，当超过该时间从属节点未收到来自管理节点心跳信息时，节点将修改节点状态为备选节点，任期增加，重置计时器时间，随即增加一段起始时间，并广播竞选信息。与Raft算法可能出现的选票瓜分情况相似，本节方案中仍然有可能出现多个备选节点。不同之处在于，备选节点在接收到其余备选节点的竞选信息时，将额外对比竞选信息RequestVote RPC中以无符号浮点数保存的历史日志计算值，根据值的大小，判定2个备选节点在分布式系统中的稳定性程度。对于更加稳定的备选节点，保留节点状态，并继续等待其余节点的回复信息；否则备选节点将修改自身状态为从属节点，放弃所有选票，重置计时器时间。在上述方案中，多个备选节点在对比来自系统其余备选节点的竞选信息后，将只保留唯一一个备选节点，剩余的备选节点当有超过半数从属节点回复同意竞选时，则成功竞选为管理节点。当剩余的备选节点未接收到半数设备的同意回复时，将继续保留节点状态直至达到超时时间，当达到超时时间时，由于此时系统只存在唯一的备选节点，该节点将宣布成功竞选为管理节点。

1.6 LC-Raft算法选举管理节点流程

该算法在选举管理节点阶段的具体工作流程如图2所示，各从属节点通过日志项信息进行日志列表的共识确认及状态机执行，该日志项由管理节点每次发送的心跳信息AppendEntries RPC负责维护[13]。同时，心跳信息作为从属节点判断管理节点是否正常工作的判断依据，当超过计时器预先设置的计时器时间而未收到心跳信息，则从属节点认为管理节点出现故障，将修改自身状态为备选节点，计算最近2次物理时间戳之间的历史日志计算值，并增加任期号，广播竞选信息RequestVote RPC[14]。在广播信息中LC-Raft一致性算法额外增加了以无符号浮点数格式保存的历史日志计算值，该数值综合计算了节点近期固定时段内发生异常响应次数以及正常运行总时长。

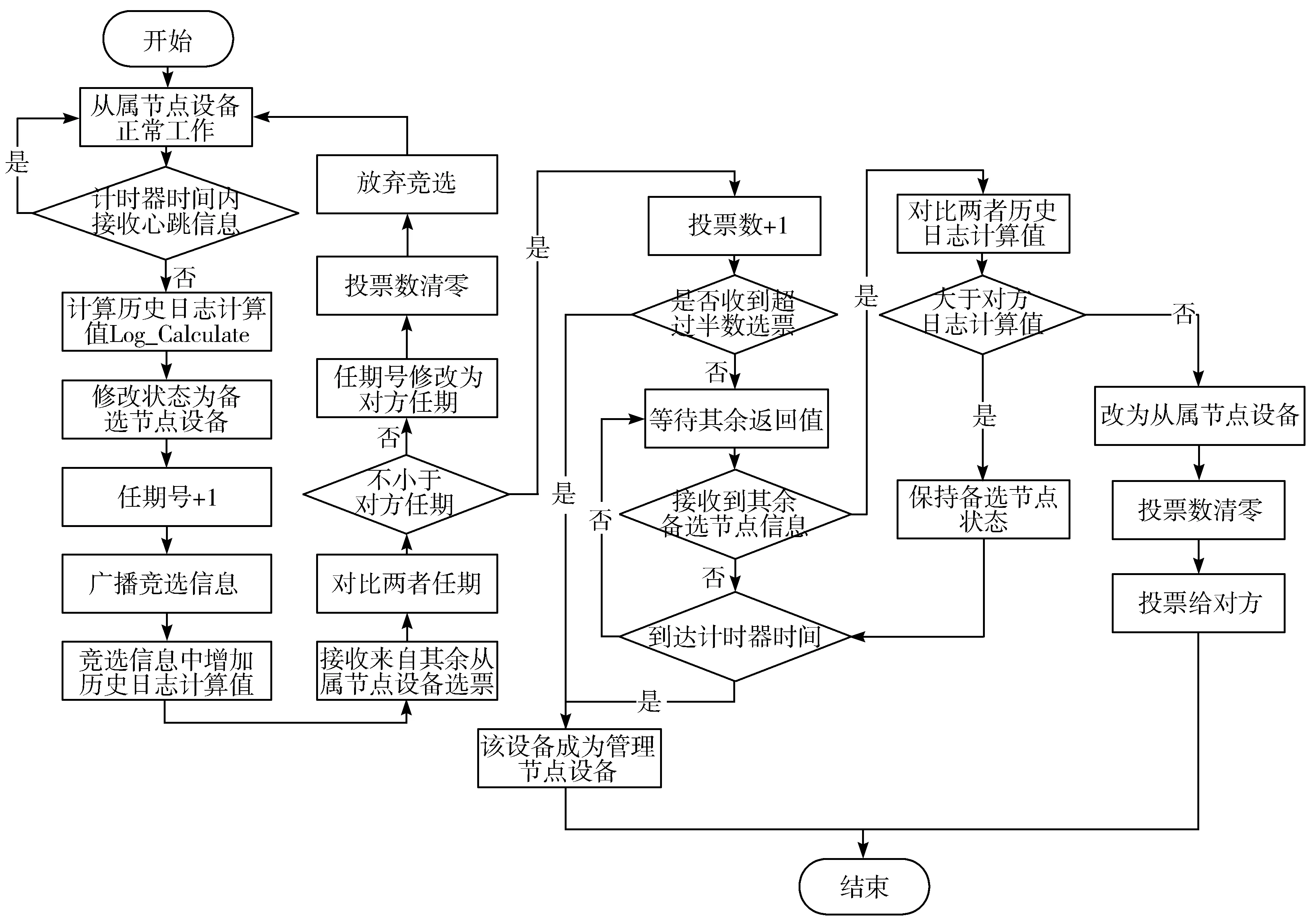
图2 LC-Raft一致性算法选举过程工作流程图

当备选节点接收到其余从属节点的回复信息时，需要对比两者任期值，当任期值小于对方时，备选节点将修改自身任期为对方任期，并清空投票，放弃竞选，重置计时器时间，将节点状态恢复为从属节点；否则，当回复信息为同意竞选时，该备选节点会增加投票数，当备选节点投票数超过半数节点数量时，则此次竞选结束[15]，该备选节点成功成为管理节点，广播心跳信息，表示此分布式系统结束重新选举，并恢复工作[16]。如果备选节点接收到来自其余备选节点的广播竞选信息，将通过比对附加在竞选信息中的Log_Calculate数值，以判断2个节点的稳定性程度，当该备选节点稳定性大于对方备选节点时，则保留备选节点状态，反之将节点状态修改为从属节点，并清空投票数，同意对方节点竞选。

经过上述步骤，分布式环境将保留唯一的备选节点，若仍未在计时器时间内收到半数以上选票，该备选节点达到超时时间后，将宣布成功竞选为管理节点，并广播心跳信息告知其余所有节点恢复正常工作状态。

2 实验与分析

本章针对改进的LC-Raft算法的选举管理节点部分核心设计模块加以实验论证。在实际运行环境中，节点通信采用RPC方式实现，实验中继续沿用原Raft算法中的Golang Channel方式实现RPC通信[17]。LC-Raft算法在迁移至运行环境时，对外提供与原Raft算法一致的接口，运行环境中其余模块无需发生改变。

实验拟在不同节点规模的分布式系统中模拟因管理节点故障而进行重新选举的过程，分布式环境中节点规模从5个节点到80个节点递增。在每个规模的选举过程中，模拟出所有节点任期值不完全相同的场景，以增加实验的复杂性，从而更加贴合实际应用环境。同时，为了避免实验偶然性，在每个节点规模中，改进的LC-Raft算法与原Raft算法均重复对比实验500次，取统计值作为评价指标，以增加实验可信度。

2.1 测试方案分析

为了验证上文提出的LC-Raft算法在重新竞选管理节点部分的性能指标，作以下方案设定：

1)以不同规模的物理节点作为测试节点进行部署。为了验证该算法在不同节点规模的分布式环境中与原Raft算法的性能差异，可以采用对不同规模下各个节点设备的测试环境配置及统一调度的方案。然而，当测试规模增大时，需要购买或租用大量的物理设备作为测试节点，并对每台设备进行测试环境配置，从操作复杂性角度及经济成本控制角度出发，此方案仅能在小规模分布式系统中进行实验测试，具有一定的局限性[18]。

2)使用虚拟机模拟测试节点在少量服务器上进行部署。此方案在一台或多台服务器上的硬件层面上实现虚拟化，通过在宿主机操作系统中运行虚拟机操作系统，实现资源的隔离性，从而模拟出多个可用于验证算法性能的测试节点[19]。此方案相比于第1种方案而言，操作复杂性得到一定程度的降低，同时仅需少量设备即可实现。与此同时，虚拟机操作系统需要额外的CPU及内存消耗，占用资源较大，无法大规模运行在单台服务器上[20]。此外，为了避免测试实验的偶然性，对于同一规模的性能测试需要重复多次后取统计值加以分析，虚拟机模拟的测试节点部署速度较慢，10 s左右的启动速度也成为限制该方案进一步优化的瓶颈所在。

3)使用容器技术模拟测试节点在单台服务器上进行部署。相比于虚拟机方案，基于Linux容器虚拟技术(Linux Container)的Docker轻量级虚拟化技术更加灵活轻便[21]。Docker容器能够与宿主机共享操作系统，通过命名空间实现资源之间的隔离，构造出多个类似“沙箱”的小规模环境，在运行时几乎无额外的性能损失，从而模拟出多个相互独立的测试节点[22]。在此基础上，该方案中单台服务器具有以脚本方式秒级增删数十台容器的优势，在同一节点规模下，可以快速分析验证LC-Raft算法与Raft算法多次测试的统计值。

综合上述方案分析，本节选用容器技术模拟LC-Raft算法与Raft算法在不同测试规模下的测试节点，实验中所有节点均以容器方式实现。为了简化描述，下述节点与容器表述均为一致。具体实验参数列表如表2所示。

表2 实验环境配置参数

在单台服务器中，通过Shell脚本指令及基础镜像，可以实现测试节点实验配置环境的批量部署。由于Docker自带的Docker Swarm容器编排工具中使用源生的Raft算法作为分布式一致性工具[23]，且改进的LC-Raft算法具有与原Raft算法一致的对外接口，实验中，通过修改Docker Swarm分别调用上述2个不同算法，实现LC-Raft算法与Raft算法在多个节点规模下的管理节点竞选性能对比。

在基础数值配置上，2种算法均设定管理节点的心跳时间为30 ms，初始所有节点任期值均设置为1，并且计时器时间为300 ms，从属节点在超过该时间未接收到来自管理节点的心跳信息则认定超时。经过测试分析，备选节点在实验分布式环境中，发布竞选信息RequestVote RPC到接收到从属节点的回复信息，时间大致在18 ms～27 ms之间。

在服务器上部署的各个容器，稳定性依赖于此服务器设备，在一定程度上并不能体现智能终端设备的不稳定性。为了模拟出类似于终端设备的不稳定程度，实验在每个容器初始化时通过脚本方式设置了不同的开关频率。为了简化实验流程，对于异常事件统计部分，只考虑由于容器关闭、重启所导致的不稳定性，并未模拟网络故障、读写IO故障等情况。同时，为了保证实验的可操作性，在一定程度缩减了正常运行时间、异常时间、统计周期的时间尺度，采用随机时间脚本方式加以修改。其中设置每次运行时间介于5 min～10 min之间，断开时间介于10 s～20 s之间。例如，容器A第1次正常运行时间为7.5 min，断开后间隔12 s恢复运行；第2次运行时间8 min，在断开后间隔10 s再一次正常运行。相邻物理时间戳之间设置为1 h的固定时段，统计最近时段内每个容器的断开次数以及运行总时长，以此计算每个容器的Log_Calculate值。重复开关容器方式的目的在于对各容器设定不同的异常响应次数及正常运行时间，上述操作所计算出的对应Log_Calculate值将作为后续各容器在选举过程中的二次评价指标。在计算结束后，不再对各容器进行重复开关，使得各容器在选举过程中正常运行，避免因容器的频繁上下线影响实验结果的有效性。

由于实验中需要设定所有节点任期不完全相同，以模拟出实际应用场景中选举阶段的复杂性，本实验选用下述方案实现，具体由Shell脚本负责执行操作：在由N个容器模拟的分布式环境中，在已初始化部署实现容器集群后，断开管理节点与其余节点之间的网络连接；同时对于其余从属节点，断开介于[0,N/2-1)之间随机个数的容器网络。在上述操作之后，仍保留网络连接的剩余容器将进行新一轮的管理节点竞选，当竞选完成时，新的容器集群中所有容器节点任期均比断开网络连接的容器节点至少+1，从而确保N个容器节点任期不完全相同。在完成上述步骤后，断开新的管理节点网络，并重新恢复原来断开网络的所有容器网络，从而模拟出不同任期的不同容器节点在管理节点故障时进行的竞选过程。该过程的操作流程如图3所示。

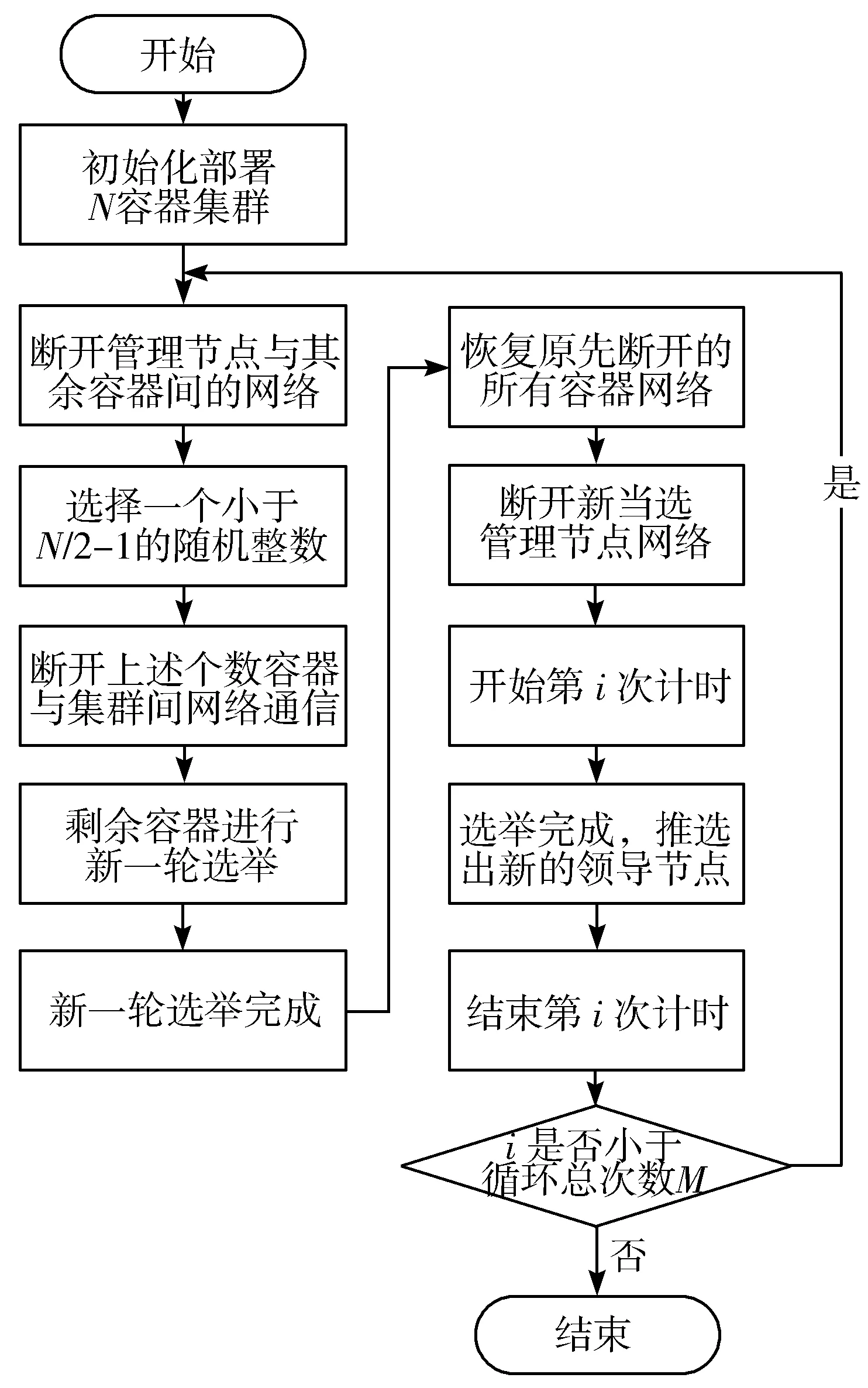
图3 固定节点情况下管理节点选举耗时计算流程图

根据上述方案，通过计算第i次结束时间减去第i次开始时间的值，可以得到在固定节点数情况下第i次选举总耗时。根据算法机制分析，该数值取决于3个因素变量：节点超时时间t1、节点接收到心跳信息后的预设随机时间值t2、节点从宣布竞选到成功竞选管理节点的耗时t3。关于t2部分的取值，本实验选择t2为介于[0,100] ms之间的随机数。

选举总耗时T计算公式如公式(2)所示。其中，t1-t2为第1阶段的计时，此时从属节点在发出对上一条心跳信息回复之后，等待到超时时间仍未收到来自管理节点的心跳信息；t3为第2阶段计时，此时从属节点已达到超时时间，将节点状态修改为备选节点，并广播RequestVote RPC信息，直到宣布竞选完成，成为新的管理节点。

T=t1-t2+t3

(2)

在对比实验中，选择Raft作为对比算法，进行选举过程的时间指标统计。由于本文提出的LC-Raft算法，主要针对原有Raft算法在选举阶段可能出现的超时情况加以改进，在其余逻辑时间戳等方面未作变动，并不会影响算法在集群正常运行时心跳信息中的日志一致性，也不会影响后续状态机读写性能。因此，本文考虑只在选举过程的各个性能指标上做出实验对比及数据分析。

实验中将按照上述耗时计算流程图计算每次不同任期节点竞选管理节点的用时开销，并根据预设的循环次数重复多次，记录下各个节点数情况下基于LC-Raft一致性算法或Raft一致性算法选举耗时的统计值。由于实验目的主要在于验证改进的LC-Raft算法在竞选管理节点时是否能够有效避免因选票瓜分导致的多次超时选举，因此在每个固定节点数统计值分析中主要需要考虑以下3个参数：选举最长耗时、选举平均耗时、标准差。

其中，统计选举最长耗时意义在于判断2种算法应对选票瓜分时最差将经历几次超时选举。由于t1为固定数值，t2为介于[0,t1]之间的随机数值，对于统计值结果影响并不大，因此，LC-Raft算法与Raft算法在选举耗时的性能对比上主要取决于节点从宣布竞选到成功竞选管理节点的耗时t3。t3数值的大小，具体反映了选举是否经历了选票瓜分带来的超时选举。鉴于上述分析，选举最长耗时可以反映出在固定节点次数情况下，2种算法应对选票瓜分情况的能力。

2.2 实验数据分析

对于上述实验方案，对应的统计结果如图4～图6所示，分别对应为选举最长耗时对比图、选举平均耗时对比图及标准差值对比图。

图4 选举最长耗时对比图

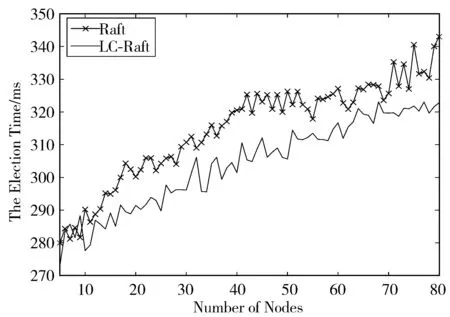
图5 选举平均耗时对比图

图6 算法标准差值对比折线图

由图4可知，在最差情况下，Raft算法对应的最长选举总时长在大致情况下与分布式环境节点数量呈现正相关关系。尽管各个节点存在随机的起始时间及统一的超时时间上限，在一定程度上能避免不同节点同时因达到超时时间而发起竞选广播，但由于备选节点在选举阶段广播RequestVote RPC过程存在通信开销，在最先发起竞选的备选节点广播信息未到达从属节点时，其余从属节点存在一定概率已达到超时时间，并再次发起广播竞选。当对应节点数增加时，统计结果中最长选举总时长整体表现为增长趋势，情况恶化程度增加。其中，当节点数介于5～55之间时，由统计结果可知，最长选举耗时在500次循环实验中最多经历了5次超时选举，最少对应2次超时选举。当节点数介于56～80时，最多经历6次超时选举，最少经历4次超时选举。

上述结果表明，原Raft一致性算法在竞选管理节点机制上并不能完全避免超时选举，存在一定概率会因为多次超时造成分布式环境选举过程缓慢，改进后的LC-Raft一致性算法在选举阶段能够避免出现因选票瓜分导致的多次超时选举，有效实现在最多一次超时时间内完成分布式系统的恢复，重新选举出新的管理节点。

在统计各个节点规模分布式环境下，选用2种一致性算法进行选举的平均耗时状态如图5所示。可见当节点数量增加时，采用Raft算法及LC-Raft算法均不可避免地会呈现出选举耗时均值增加的情况，表明节点数量增加会恶化一致性算法在管理节点选举过程的表现能力。同时，由曲线可知，改进后的LC-Raft算法在选举平均耗时均值增长斜率较Raft算法更加平缓，除去5～10个节点规模中个别情况均值表现较Raft算法更差之外，整体均值表现均优于原Raft算法。表明LC-Raft一致性算法在平均情况下，选举耗时开销普遍小于原Raft一致性算法。

图6为2种算法在各个节点规模下的标准差值对比折线图，标准差的大小表明在某个节点规模下，2种一致性算法在选举过程耗时的稳定程度。由图6可知，LC-Raft算法与Raft算法随着节点数量增加，选举耗时的不稳定程度呈现增加的趋势，同时，由于图中Raft对应数值在大部分情况下均大于LC-Raft算法对应数值，表明改进的LC-Raft一致性算法的稳定性在节点规模为11～80之间时，均优于原Raft一致性算法。

本实验通过在各个节点规模的多次循环实验，对改进的LC-Raft一致性算法及原Raft一致性算法在选举阶段的耗时性能方面做了相应统计验证，结论如下：

1)改进后的LC-Raft一致性算法在选举阶段能够避免由于选票瓜分而引起的多次超时选举，有效实现了在最多一次超时时间内完成分布式系统的恢复，重新选举出新的管理节点。

2)LC-Raft一致性算法在同样节点规模情况下，大部分选举耗时均值少于原Raft算法，体现了该算法在选举阶段的可用性。

3)在稳定性方面，LC-Raft一致性算法的选举耗时较原Raft算法更加稳定，出现极端情况较少，不存在因多次选票瓜分导致的多次超时选举过程。

3 结束语

本文实现了一种基于历史日志计算值的改进一致性算法LC-Raft，在分布式系统的重新选举阶段，能够实现在短时间内实现推举出具有较好稳定性的管理节点，同时避免出现多次超时选举的极端情况。并且基于Docker容器引擎，设计了一套在单台服务器上模拟实现各种节点规模选举过程的实验环境，通过多次实验统计值验证了本算法在选举过程中的良好性能，具有一定的实际应用价值。