铁路钢板运输装载方案装载量计算方法研究

2020-12-31杨广全马欣然

铁道货运 2020年12期

杨广全，胡淦，马欣然

(中国铁道科学研究院集团有限公司运输及经济研究所，北京 100081)

钢板是铁路货物运输的重要品类，常用规格的板厚 6 ～ 80 mm、板宽 1.5 ～ 3.2 m、板长 3 ～ 12 m，目前钢板铁路运输主要按《铁路货物装载加固规则》的定型方案采用敞车、平车组织装车[1]。钢板可视为一种线性弹性梁，其刚度与钢板的长度、厚度有关，钢板厚度越薄、长度越长，在垂直方向极易产生弯曲变形[2-3]。钢板采用支垫分层，沿车辆纵、横向中心线对称装载，装载后钢板的总重心投影落在车地板纵横中心线交点上，确保车辆不偏载、不偏重。钢板的重量通过支垫传递到车地板上，车辆承受多作用点的集中载荷。当采用敞车以《铁路货物装载加固规则》中定型方案2支承方式装车时，除个别厚度较大的钢板外，大部分钢板装载后存在下挠(塌腰)现象，同时由于敞车集载能力的问题，绝大部分规格的钢板使用通用敞车按定型方案装车时难以实现满载，一般情况下钢板的厚度越小，亏吨情况越严重，相应地增加了钢板的运输成本。由于铁路敞车集载能力的限制，装运时应根据钢板的规格确定合理装载量[4-5]，减少钢板的装载亏吨问题。因此，针对钢板的厚度和长度，以《铁路货物装载加固规则》规定的技术条件为依据，提出铁路钢板运输装载方案装载量计算方法，通过计算方案的理论装载量，优化钢板运输装载方案设计，提高钢板运输装载加固方案的经济性、安全性和可靠性。

1 铁路钢板运输装载方案装载量计算方法

根据钢板装载方式，钢板除了在支点处承受支反力外，仅承受自重均布载荷作用。由于其他钢板通过草支垫或垫木施加于该钢板的压力或支撑力不会引起该钢板内力变化，因而可以对单块钢板进行独立力学分析和计算。依据单块钢板的受力和钢板装载结构，基于力学平衡，可计算出车辆承受的集中载荷，从而确定车辆中央工作弯矩M工作。设M允许表示车辆中央最大允许弯矩，在M工作≤M允许的条件下，设计钢板装载结构，使钢板装载量最大，达到钢板装载方案优化设计的目的。

1.1 钢板基本力学模型构建及求解

将单块钢板视为具有n个支点，支点之间存在高度差的连续梁。以支点1为原点建立坐标系，δi表示支点i相对于支点1的高度偏差，取正值表示支点i高于支点1，取负值表示支点i低于支点1，记连续梁左右侧悬臂长度分别为l1，ln+1，梁中各简支梁的跨度从左向右依次为l2，l3，…，ln，则具有高度差的n支点连续梁力学模型如图1所示。

n个支点处共有n个支反力，分别用F1，F2，…，Fn表示，求解n个支点支反力的问题属于连续梁的高次超静定问题。为了求解该问题，在所有中间支座处将梁切开，并换为铰链连接，即基本系统为一系列简支梁。在每个简支梁上，仅承受直接作用于该跨的自重均布载荷及两端的支点弯矩，因而可求出梁端的转角，并根据中间支座处相连两截面的转角相同的条件，建立补充方程，确定全部支点弯矩，从而确定单块钢板的支反力。

1.2 支点弯矩计算

支点i处的左、右跨简支梁如图2所示。考虑图2支点i处的左、右两跨简支梁，在左跨(即第i跨)简支梁上，作用有支点i处弯矩Mi、支点i-1处弯矩Mi-1及自重均布载荷q；在右跨(即第i+1跨)简支梁上，作用有支点i处弯矩Mi、支点i+1处弯矩Mi+1及自重均布载荷q。

支点高差引起的初始转角如图3所示。分析并确定左跨简支梁上右端截面i处的转角由左跨简支梁支点高差在支点i处引起的初始转角左跨简支梁自重均布载荷在支点i处产生的转角及左跨简支梁上的支点弯矩Mi与Mi-1在支点i处产生的转角组成。因此，左跨简支梁截面i的总转角可表示为

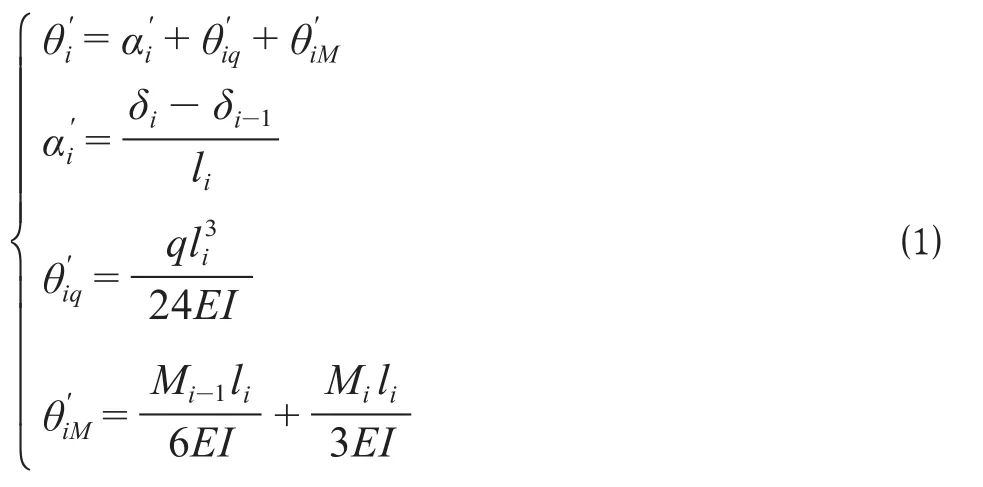
式中：E为钢板的弹性模量；I为钢板的垂向惯性矩；Mi为支点i处的弯矩。

同理，分析并确定右跨简支梁上左端截面i处的转角由右跨简支梁支点高差在支点i处引起的初始转角右跨简支梁自重均布载荷在支点i处产生的转角及右跨简支梁上的支点弯矩Mi与Mi+1在支点i处产生的转角组成。右跨简支梁左端截面i的总转角可表示为

图1 具有高度差的n支点连续梁力学模型Fig.1 Dynamics model of continuous beam having n fulcrums with height difference

图2 支点i处的左、右跨简支梁Fig.2 Left and right span simply supported beams at fulcrum i

图3 支点高差引起的初始转角Fig.3 Initial rotation angle caused by height difference of fulcrum

支点i处转角连续条件如图4所示，在中间支点i处，左、右相连两截面的转角相同，即

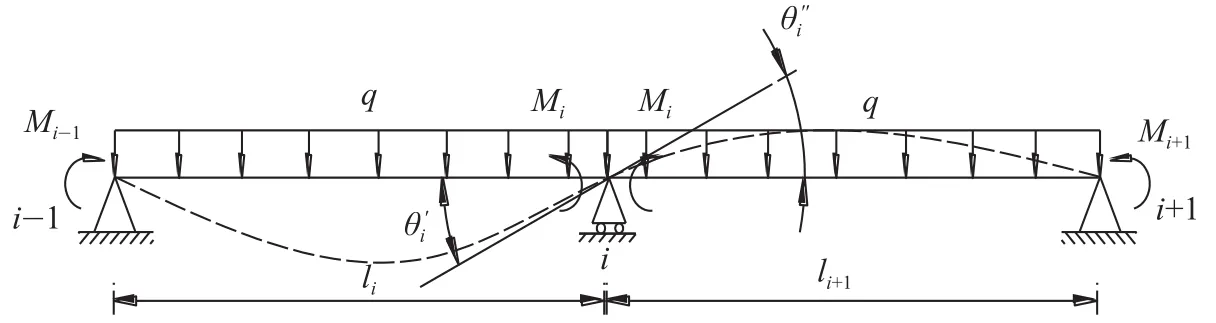
图4 支点i处转角连续条件Fig.4 Continuous condition of rotation angle at the fulcrum i

将公式 ⑴、公式 ⑵ 代入公式 ⑶，得补充方程为

对于支点1和支点n，弯矩分别为

式中：M1为钢板连续梁的左侧悬臂在支点1处产生的弯矩；Mn为钢板连续梁的右侧悬臂在支点n处产生的弯矩。

由图1可知，连续梁具有n-2个中间支点，根据公式 ⑷，即可建立具有n-2个方程的线性方程组，以公式 ⑸ 和公式 ⑹ 为初始条件，求解该线性方程组，即可求出n-2个未知的支点弯矩。

1.3 钢板的支反力计算

支点弯矩确定后，结合各简支梁上承受的自重均布载荷，可求出各简支梁的支反力，并计算相邻简支梁在共同支座处的支反力的代数和，即得连续梁的支反力。支点i处的左、右跨简支梁受力分析如图5所示。

计算连续梁在支点i处的支反力Fi。对于各简支梁，承受支点弯矩、自重均布载荷的作用，受力平衡，对支点i-1处求力矩，计算公式为

式中：为支点i处的左跨简支梁承受的支点弯矩Mi-1，Mi及自重均布载荷q在支点i处的支反力。

对支点i+1处求力矩，计算公式为

式中：为支点i处的右跨简支梁承受的支点弯矩Mi，Mi+1及自重均布载荷q在支点i处的支反力。

连续梁支点i处支反力计算公式为

对于支点1和支点n，其支反力计算公式分别为

图5 支点i处的左、右跨简支梁受力分析Fig.5 Force analysis of left and right span simply supported beams at fulcrum i

将公式 ⑼、公式 ⑽、公式 ⑾ 联立建立n维线性方程组，求出单块钢板的支点反力F1，F2，…，Fn。

1.4 钢板允许装载量的确定

单块钢板的n个支反力确定后，根据钢板的对称装载结构，计算车辆在装载2块钢板时承受的集中载荷。由于货物对称装载时车辆的最大工作弯曲力矩产生于车辆中央，根据车辆承受2块钢板的集中载荷，计算车辆中央承受弯矩，进而确定钢板理论装载量为

式中：Qmax为钢板理论装载量；Mq2为装载2块钢板时车辆中央承受的弯矩；Q为单块钢板的质量。

2 铁路钢板运输装载方案设计实例

2.1 基本技术条件及优化

为了避免敞车集重装载，铁路钢板运输装载方案需要满足以下基本技术条件：①车体主要部件的工作弯曲力矩应小于其最大容许弯曲力矩，即M工作≤M允许。根据《铁路货物装载加固规则》，60 t，61 t敞车承受对称集中载荷时的最大允许弯矩M允许为380 730 N·m，70 t敞车承受对称集中载荷时的最大允许弯矩M允许为635 922 N·m，作为钢板理论装载量计算的依据；②钢板装车后车体主要部件(中梁、侧梁、横梁、枕梁等)的工作应力要小于其许用应力，作为车辆强度校核的依据。

根据铁路钢板运输装载方案基本技术条件，钢厂大部分规格的钢板可以采用敞车装运，但由于敞车集载能力的限制，为提高钢板的装载量，在设计铁路钢板运输装载方案时可以在以下方面进行优化[6]。

（1）增加钢板装载的支点数目，使车体趋向于承受均布载荷。将定型方案的2支点支承优化为多支点支承，增加支点数量后，降低了每个支点的承载量，即降低了作用在车地板上作用力[7-8]，使钢板载荷近似于均布载荷分布在车地板上，既有利于降低车辆承载部位局部区域的应力，也可大幅度降低载荷在车辆中部引起的弯矩。

（2）合理布置支点放置位置。根据车底架结构，将支点布置在车底架的大横梁、小横梁上，通过横梁将部分载荷传递到车侧墙(梁)上，降低车底架中梁承载后的应力。

（3）采用钢板靠车辆两端墙向中部叠装的方式。采用钢板靠车辆两端墙向中部叠装的方式，可使部分钢板载荷作用在车辆转向架台车上，尽可能降低叠装部分钢板在车辆中部引起的弯矩。当所装载的钢板数目为偶数时，钢板靠车辆两端墙向车辆中部叠装装载；当所装载的钢板为单数时，先将第1块钢板沿车辆对称装载，再将其余钢板靠车辆两端墙向车辆中部依次叠装装载。

2.2 钢板装载方案设计

拟采用60 t，61 t通用敞车装运10 m长钢板，为了使车辆受力均匀，车辆地板上设置了6个支点，并将支点布置在车底架的大横梁、小横梁上，通过横梁将部分载荷传递到车侧墙(梁)上，降低车底架中梁承载后的应力；钢板靠车辆两端墙向中部叠装装载，以降低叠装部分钢板在车辆中部引起的弯矩，进而提高钢板的装载量。为了保证钢板对称装载，钢板的装载数目为偶数。60 t，61 t通用敞车装载长10 m钢板的装载加固方案示意图如图6所示。

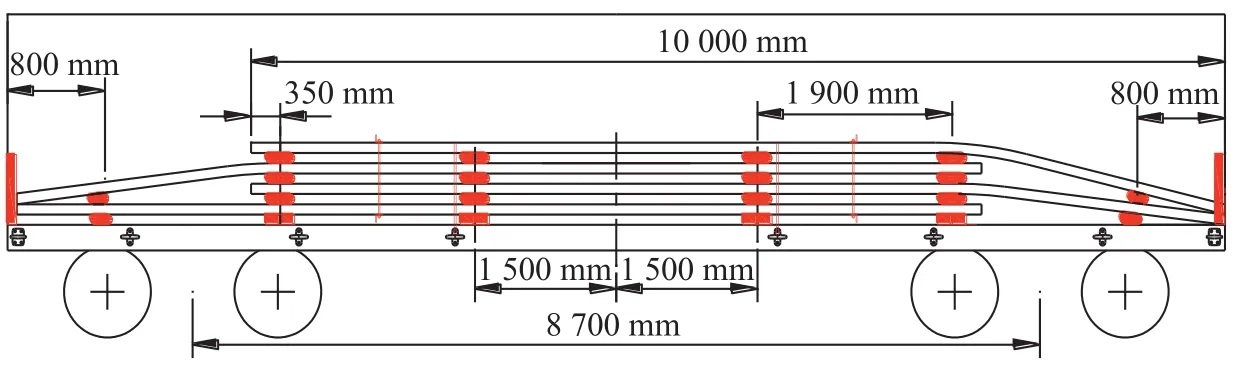
图6 60 t，61 t通用敞车装载长10 m钢板的装载加固方案示意图Fig.6 Loading reinforcement scheme of 10-meter steel plate loading onto 60t/61t open wagon

拟装载钢板的长度L= 10 m，宽度W= 2.5 m，厚度H= 16 mm，密度为7.8 t/m3，弹性模量E= 200 GPa，则钢板的质量Q为

Q=L×W×H×7.8 = 10×2.5×0.016×7.8 = 3.12 t

钢板的自重均布载荷q为

q= 9.8×1 000Q/L= 9.8×1 000×3.12 / 10 = 3 057.6 N/m

钢板的惯性矩I为

根据图6所示的钢板装载结构，选取底部单块钢板建立基本力学模型，支点数n= 5，钢板的悬臂长度及跨度从左到右依次为l1= 0.8 m，l2= 2.05 m，l3= 1.9 m，l4= 3 m，l5= 1.9 m，l6= 0.35 m，支点高差从左向右依次为δ1，δ2，δ3，δ4，δ5。计算工况为：工况 1，δ1=δ3=δ4= 0 ；工况 2，δ1= 0，δ3=δ4=-20 mm；工况 3，δ3=δ4= -20 mm ；工况 4，δ1=-40 mm，δ3=δ4= -20 mm ；工况 5，δ1= -80 mm，δ3=δ4= -20 mm ；工况 6，δ1= 0 mm，δ3=δ4= -40 mm ；工况 7，δ1= -20 mm，δ3=δ4= -40 mm；工况 8，δ1=-40 mm，δ3=δ4= -40 mm ；工况 9，δ1= -80 mm，δ3=δ4= -40 mm。根据支点高差不同组合工况，依据公式 ⑼、公式 ⑽、公式 ⑾ 建立的5维线性方程组，计算钢板支点反力。单块钢板支点反力计算结果如表1所示。

表1 单块钢板支点反力计算结果 NTab.1 Computational results of support reaction with single steel plate

根据钢板的对称装载结构，计算车辆在装载2块钢板时承受的集中载荷T1～T6，即T1=T2=F1，T2=T5=F2+F5，T3=T4=F3+F4，车辆2个转向架承受的钢板质量均为Q。根据力矩平衡，计算车辆中央承受弯矩为

式中：LC为车辆转向架中心距，为8.7 m。

计算车辆承受2块钢板时车辆中央弯矩Mq2如表2所示。

根据计算结果，支点高差δ1，δ2，δ4增加时，车辆承受的中央弯矩减小；当δ3=δ4= -40 mm，δ1= -80 mm时，车辆中央承受的弯矩最小，为10 460 N·m，据此确定钢板理论装载量为

Qmax=M允许/ (2×Mq2)×Q= 380 730 / (2×10 460)×3.12 = 56.78 t

由于每块钢板为3.12 t，且钢板装载数目为偶数，通过计算可装载18块钢板，实际所装载的钢板质量为56.16 t。因此，通过布置合适的支点位置，选择合适的支点高差分布及高差值，不仅可以增大装载量，并且可以改善车辆承载分布，将车辆承受的力向车辆枕梁转移，改善车辆的承载状况。

2.3 钢板装载加固方案试验验证

为了验证钢板装载加固方案的可行性，开展静载试验和冲击试验。静载试验主要测试按装载方案装载状态下车辆主结构的强度及钢板挠度情况，应力测点布置在敞车中梁、侧梁、大横梁、小横梁上。冲击试验主要测试钢板的加固状态。冲击试验模拟铁路车站调车作业过程，冲击速度逐步增加，采用单端连续冲击的方式进行，记录钢板位移数据和装载加固状态。试验结果表明：①静态加载后车辆主结构最大应力小于车辆材料许用应力值。钢板最大挠度发生在3 m跨处，测量钢板最大挠度为6 mm，钢板挠度符合要求；②经过10次冲击试验后，所装载钢板纵向位移较小，加固状态满足《铁路货物装载加固要求》。

3 结束语

货物装载加固和货车满载工作技术性强，是铁路运输工作的重要组成部分。钢板作为铁路货物运输的重要品类，由于型号规格较多，钢板装运亏吨问题较大影响了钢板装载加固方案的制定质量，制约铁路货车装载钢板的装载量和运用经济性。铁路钢板运输装载方案装载量计算方法研究，通过计算在不同支点高差分布下出铁路钢板运输装载方案的理论装载量，实现了铁路钢板运输装载方案的优化设计。应综合考虑《铁路货物装载加固规则》的技术要求、钢板规格和钢板力学特点进行定制化设计，在确保钢板装载加固方案安全可靠的前提下，重点提高铁路钢板运输装载量，设计出具有市场竞争力的钢板铁路运输产品，以提高铁路钢板运输经济效益，推动铁路钢板运输发展。