垂直发射舰载火箭弹出筒姿态研究

欧阳福蕾，李 磊，龚春林，刘佳琪

（1.北京航天长征飞行器研究所，北京，100076；2.西北工业大学航天学院，西安，710072）

0 引 言

21 世纪，海军作战从大洋转向近海，不仅要有制海能力，而且要有对地攻击能力。依托海上舰艇平台对陆地（或岛屿）上的固定目标进行精确打击，是海军作战任务的重要组成部分，对近海作战、维护海洋权益、打击恐怖主义具有十分重要的现实意义[1]。

舰载火箭弹与陆基火箭弹的最大区别在于发射载体是海平面上运动的动基座。在适配器出筒前，火箭弹在适配器约束下随同动基座运动，即跟随舰船一起运动[2]。舰载火箭弹的出筒运动参量主要有出筒速度、姿态角和角速度，是火箭弹飞行的起始条件。初始扰动是影响舰载火箭弹发射精度的主要因素[3]，舰载火箭弹的发射精度取决于两方面因素：一是弹-架系统特性，比如推力偏心、摩擦力等；二是舰船摇摆产生的过载。为满足舰载火箭弹制导系统要求的初始发射精度，火箭弹出筒运动参数应当控制在合理范围内[4]。因此，有必要研究垂直发射舰载火箭弹的出筒姿态。

1 舰载火箭弹出筒过程动力学建模

垂直发射舰载火箭弹采用双适配器[5]，其出筒过程分为两个阶段；第1 阶段是开始运动至前适配器离筒瞬间，第2 阶段是前适配器离筒至后适配器离筒瞬间。

1.1 第1 阶段

在第1 阶段，舰载火箭弹的受力情况如图1 所示。

有：

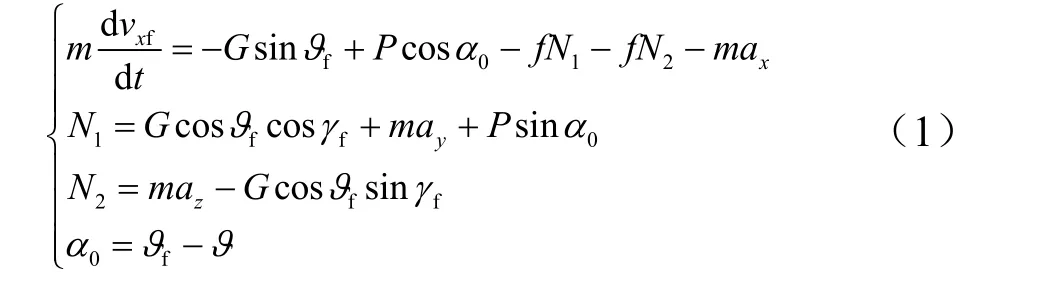
式中 ϑf,ψf,γf为垂直发射装置的姿态角；ϑ 为舰载火箭弹的姿态角；t 为滑行时间； α0为ϑ 与 ϑf两者夹角；ax为火箭弹受到的惯性加速度在 Oxf方向的分量。按照给定的滑行距离l，可求得出筒速度：

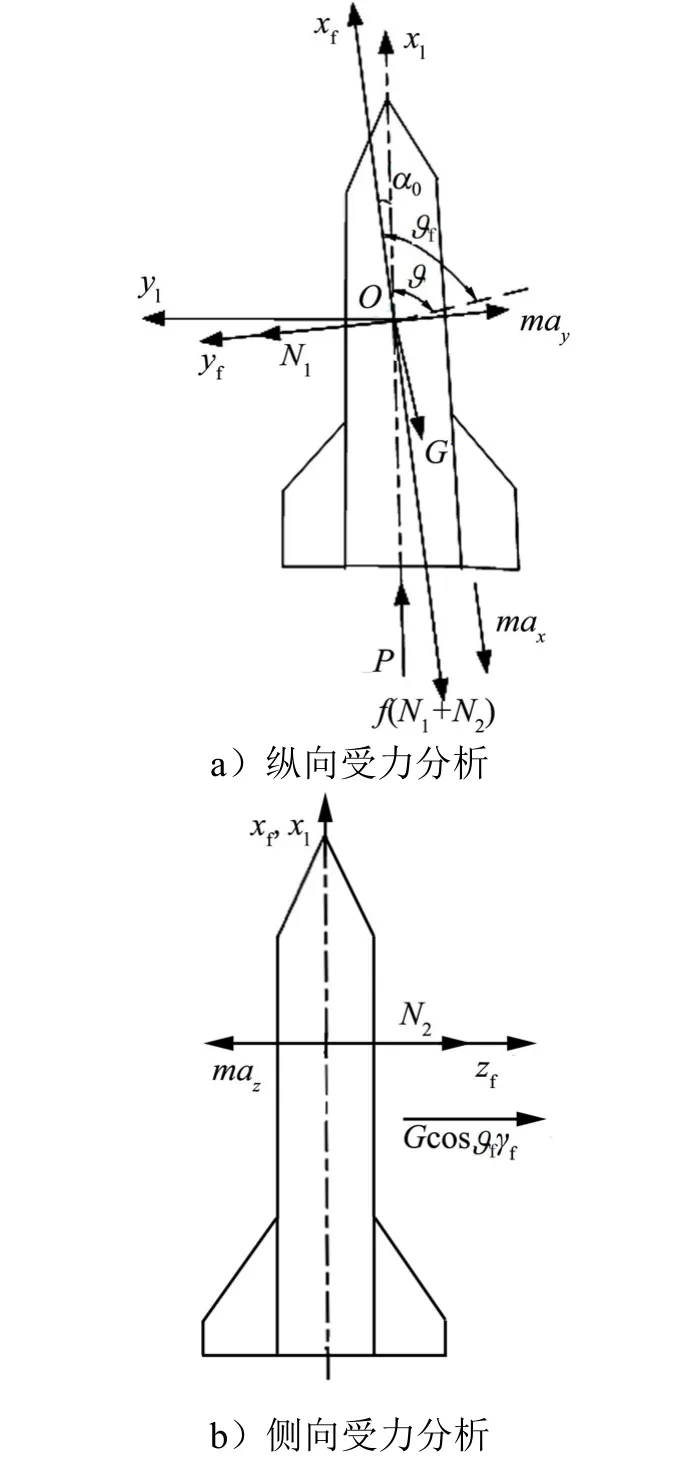
图1 第1 阶段舰载火箭弹受力分析Fig.1 Force Analysis of Shipboard Rocket in the First Stage

1.2 第2 阶段

由于前适配器出筒，后适配器仍受发射筒刚性约束，舰载火箭弹随舰船一起摇摆运动和升沉运动。火箭弹除了沿发射筒滑行之外，还有绕质心转动[7]，火箭弹质心的运动是这两种运动的复合运动，如图2 所示。

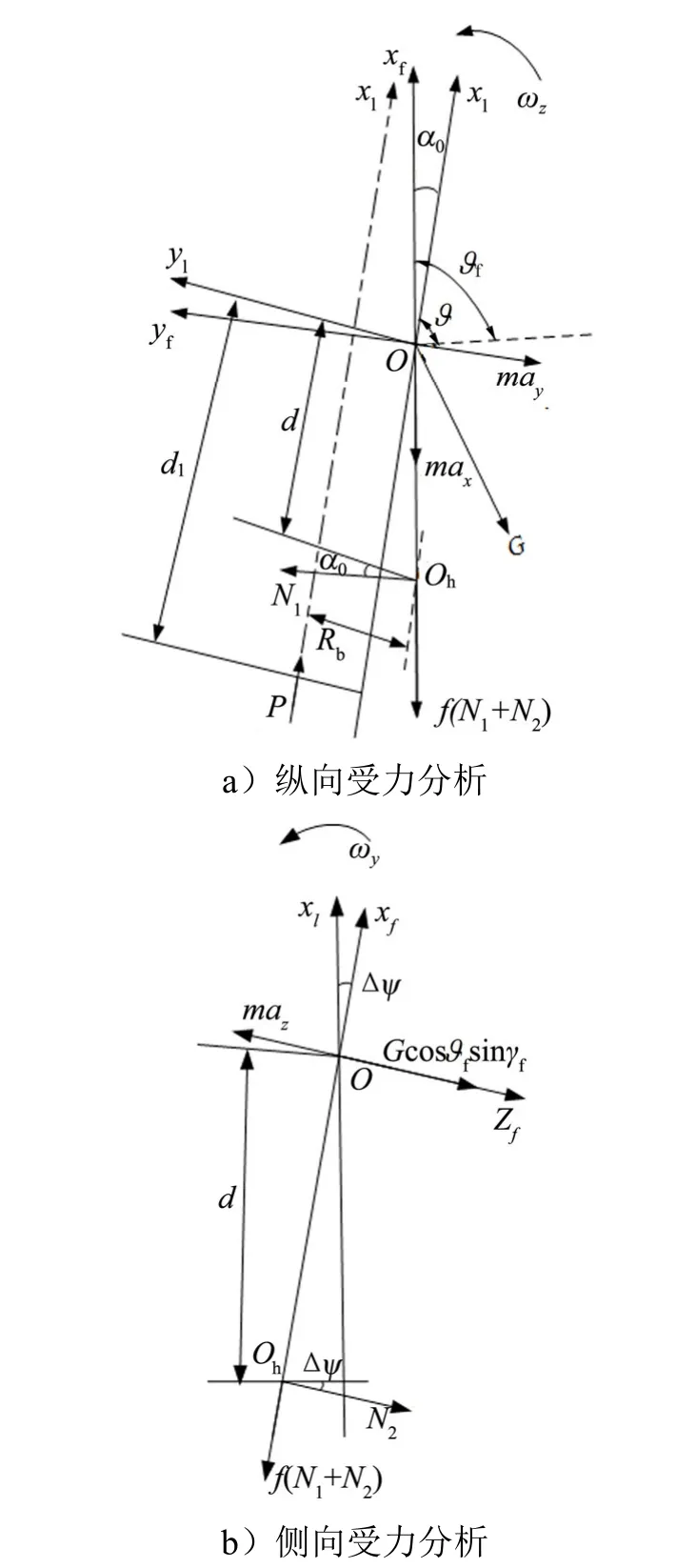
图2 第2 阶段舰载火箭弹受力分析Fig.2 Force Analysis of Shipboard Rocket in the Second Stage

建立舰载火箭弹出筒过程动力学方程为

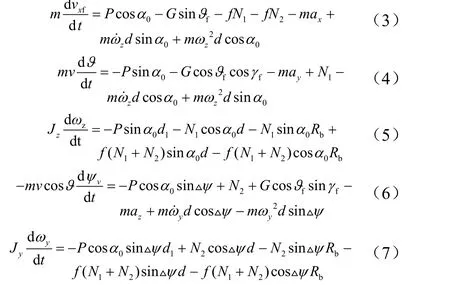
式中 △ψ =ψf-ψ； Jy， Jz分别为绕Oy 轴、Ox 轴的转动惯量。

建立舰载火箭弹运动学方程为

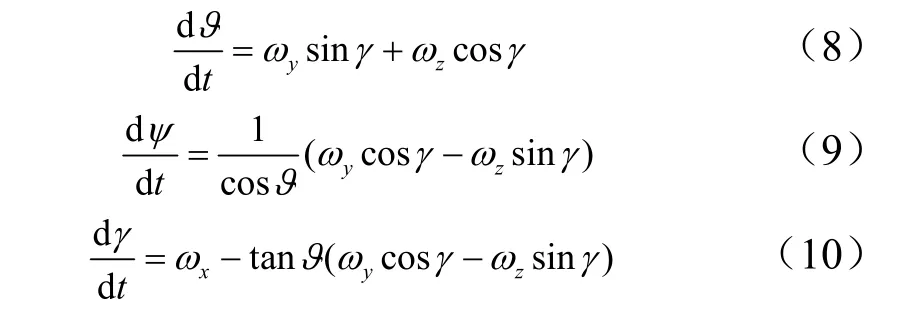
式中 γ 为火箭弹的滚动角。

2 舰载火箭弹惯性过载分析

根据舰船耐波性理论，舰船运动有在推进器作用下的运动和在海浪作用下的附加运动。按照刚体运动理论，舰船在水中的振荡是纵漂、横漂、升沉、横摇、纵摇、偏摇的耦合作用结果，只考虑影响较大的升沉、横摇和纵摇[9]。式（11）为舰船升沉运动方程和稳态的横、纵摇运动方程。

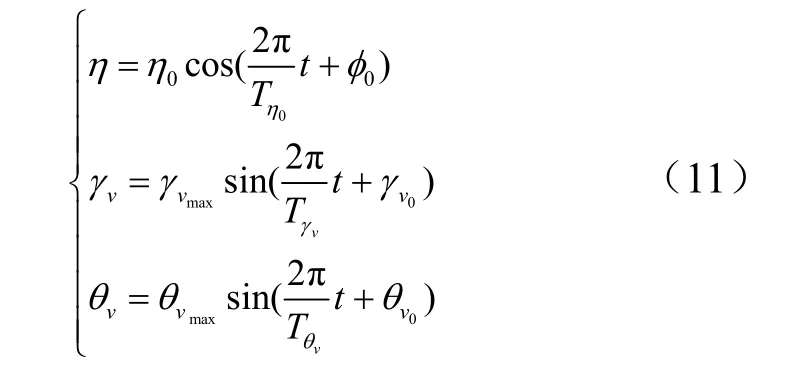
在舰船坐标系下，任意时刻舰船的摇摆角速度和角加速度为

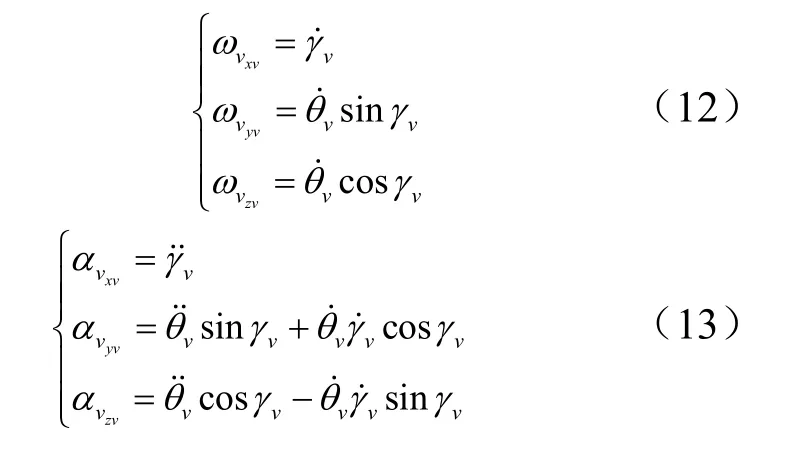
舰船与垂直发射装置固连，舰载火箭弹在发射筒运动时，质心O 点在舰船坐标系中的初始位置为( xvc, yvc, zvc)。牵连加速度 ae由舰船横纵摇产生的法向加速度 an、切向加速度 aτ和升沉运动引起的加速度 a0组成。

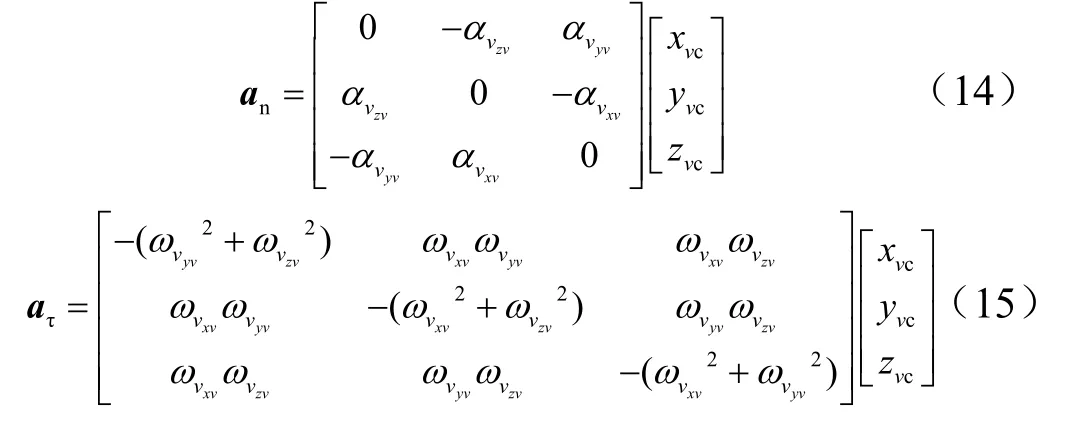
牵连加速度 ae和科氏加速度 ak之为和 av，即av= ae+ak。其中， ak= 2ωv×vr， vr为火箭弹在舰船坐标系下的相对速度。

3 仿真计算分析

3.1 舰船运动仿真

假设某舰船在5 级海情下顶浪航行，船速12.347 m/s，根据风浪等级表确定5 级海情基本参数[10]，火箭弹质心在舰船坐标系下的初始位置为(36m,7.073m,0m)。

联立式（11）和式（12），计算得到各摇摆角速度随时间变化关系，如图3 所示。摇摆速度中，ωvxv由横摇产生、幅值为0.27 rad/s， ωvyv、 ωvzv是由纵摇产生的沿坐标轴分量，ωvzv的幅值为0.14 rad/s，ωvyv幅值最小，只有0.04 rad/s。

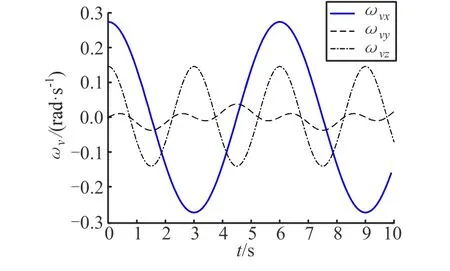
图3 摇摆角速度随时间变化Fig.3 Rocking Angle Speed Changes with Time

联立式（11）和式（13），计算得到各摇摆角加速度随时间变化如图4 所示。摇摆加速度中，avxv是由横摇产生的，avyv和avzv是由横摇和纵摇作用产生的，avyv较小，幅值仅为0.07 rad/s2, avxv和avzv的幅值为0.3 rad/s2左右。

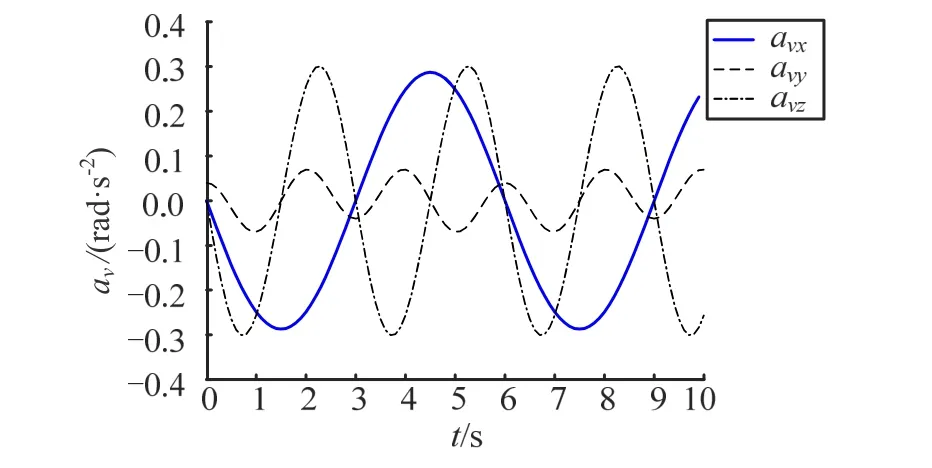
图4 摇摆角加速度随时间变化Fig.4 Rocking Angle Acceleration Changes with Time

在发射坐标系下，垂直发射装置的姿态角随时间变化如图5 所示。由于垂直发射，ϑf在90°左右波动，ψf稳定在0°左右。横摇主要产生较大的 γf，最大值为15°，与5 级海情下顶浪航行的实际符合。

图5 舰船运动产生的姿态角变化Fig.5 Attitude Angle Produced by Ship Movement

3.2 舰载火箭弹出筒姿态仿真

联立上述舰载火箭弹出筒过程计算方程和惯性过载计算方程，运用龙格-库塔数值方法求解得到出筒姿态角、角速度和速度。俯仰角ϑ 随时间变化如图6 所示。

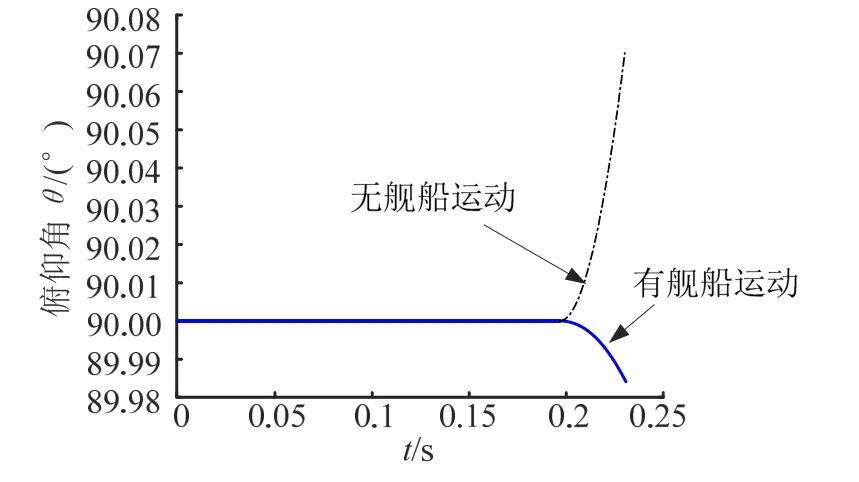
图6 俯仰角θ随时间变化Fig.6 Pitch AngleθChanges with Time

舰载火箭弹出筒过程中，第1 阶段（0～0.19 s），俯仰角保持在90°，第2 阶段（0.19～0.23 s），俯仰角相对第1 阶段有明显变化，但变化量小，从而可以忽略不计。舰船运动对俯仰角的影响小。

偏航角ψ 随时间变化如图7 所示。无舰船运动时，偏航角稳定在0°，有舰船运动时，偏航角从0°下降至-2°左右。因此，舰船运动对偏航角有一定的影响。

角速度分量 yω 随时间变化如图8 所示。无舰船运动时，角速度分量 yω 始终为零，但舰船运动使 yω 从0 rad/s 增大至0.19 rad/s，可得舰船运动对 yω 的影响较大。

角速度分量 zω 随时间变化如图9 所示。无舰船运动时，角速度分量 zω 会从0 rad/s 增至0.07 rad/s。有舰船运动时，zω 从0 rad/s 降至-0.02 rad/s 左右，所以，摇摆运动对 zω 有一定的影响。

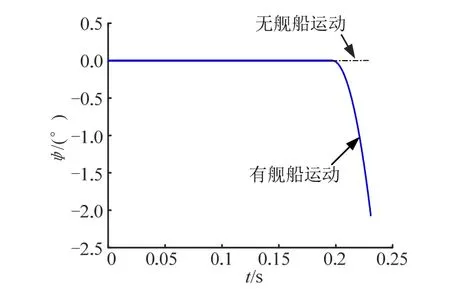
图7 偏航角ψ 随时间变化Fig.7 Yaw Angleψ Changes with Time

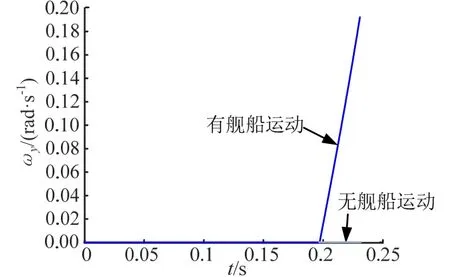
图8 角速度分量 ω y随时间变化Fig.8 Angular Velocity Componentω yChanges with Time

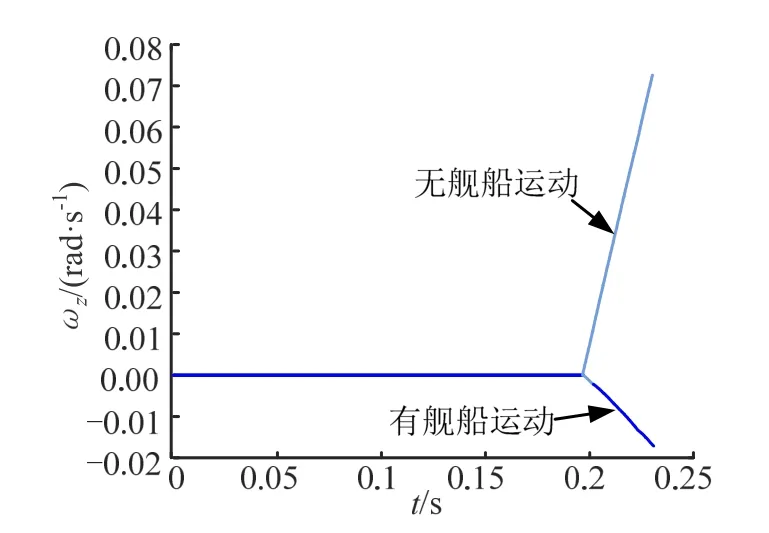
图9 角速度分量 ω z随时间变化Fig.9 Angular Velocity Componentω zChanges with Time

舰载火箭弹出筒过程中的弹道倾角θ 和弹道偏角ψv基本维持在初始状态，变化量小。因此舰船运动对弹道倾角θ 和弹道偏角ψv的影响可忽略不计，如图10和图11 所示。

联立上述模型的动力学方程和运动学方程，求解得到火箭弹出筒速度为36.6 m/s。通过做垂直发射舰载火箭弹关键技术验证试验，传感器测量出火箭弹的出筒速度为38.1 m/s，图12 为仿真速度与实验速度的对比。从图12 可见，仿真与实验结果基本一致，验证了出筒过程中数学模型的可行性和正确性。

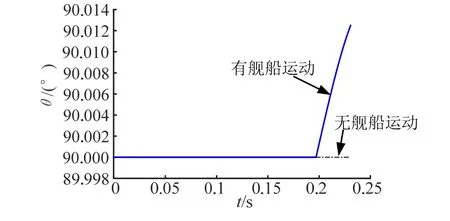
图10 弹道倾角θ 随时间变化Fig.10 Ballistic Inclinationθ Changes with Time

图11 弹道偏角ψ v随时间变化Fig.11 Ballistic Deflection Angle ψ vChanges with Time

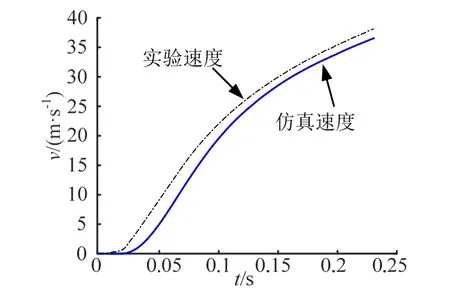
图12 仿真速度与实验速度对比Fig.12 Comparison of Simulation Speed and Experiment Speed

4 结 论

通过建立垂直发射舰载火箭弹出筒过程的动力学方程和运动学方程，分析了舰船运动、推力偏心和摩擦力的影响，结合仿真计算分析舰载火箭弹出筒过程中的运动参量，得到结论如下：

a）舰载火箭弹在出筒过程中受力状态复杂，yω 角速度和 zω 角速度在前适配器出筒后变化大。

b）俯仰角ϑ、偏航角ψ 、弹道倾角θ 和弹道偏角vψ基本维持在初始状态，舰船运动产生的影响可忽略不计。

c）对比仿真和实验结果，两者速度基本吻合，验证了模型的正确性。