运载火箭贮箱典型结构件自主统一造型方法研究

王 腾，张 茜，李 澍，聂蓉梅

（北京宇航系统工程研究所，北京，100076）

0 引 言

运载火箭的贮箱是航天运载器动力系统和结构系统的关键部件。当前国内外主流运载火箭的贮箱多为承力式贮箱[1,2]，即贮箱也是火箭箭体的外壳。贮箱的前（后）底大多为椭球形或圆球形。贮箱在概念设计时，可以通过将前（后）底用椭圆形或圆形旋转360°得到，但是在对贮箱的前（后）底详细设计时，考虑到制造的难易程度，会将贮箱的前（后）底划分为瓜瓣、叉形环、法兰以及法兰瓜瓣连接环板等几个部分。目前，中国使用三维CAD 软件完成贮箱的前（后）底详细设计，但由于设计软件均为国外的商业软件，对结构三维建模的内核进行了封装，用户无法对商软的建模原理进行自主定制和修改，随着软件升级换代及设计平台的更新和更换，有可能出现原先设计的三维模型打不开或出错的问题，且中国运载火箭产品的是否自主可控关乎国防安全，所以有必要研究自主可控且能够准确表示结构设计意图的贮箱前（后）底结构模型的统一表达方法。

贮箱模型结构的组成曲线包括直线、解析曲线等，对直线和解析曲线的统一描述常常采用NURBS 曲线，NURBS 曲线由于具有强大的造型功能，所以被主流几何造型系统使用，不仅可以表示任意曲线，还可以将规则曲线和任意曲线的表达统一起来，并通过调节权因子对曲线进行精细化控制。

1 贮箱前（后）底结构表达流程

通过对贮箱前（后）底的研究发现，贮箱前（后）底可以分解为法兰、法兰瓜瓣连接环板、瓜瓣、叉形环4 个子结构，如图1 所示。

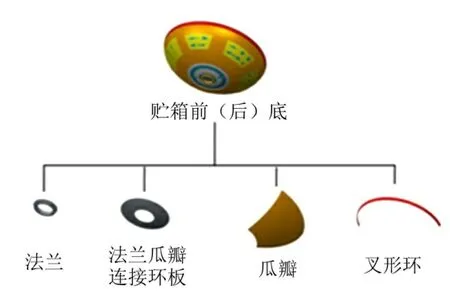
图1 贮箱前（后）底结构组成分解Fig.1 Diagram of the Ellipsoid Bottom Structure

通过对法兰、法兰瓜瓣连接环板、瓜瓣、叉形环结构特征的分析，可知贮箱前（后）底是由草图特征、旋转特征、加厚特征和布尔减运算特征组成。由于贮箱前（后）底的横截面为椭圆形，所以法兰瓜瓣连接环板、瓜瓣、叉形环结构的草图特征是由若干直线段和椭圆弧段组成。对贮箱前（后）底结构设计模型的自主表达流程如图2 所示。

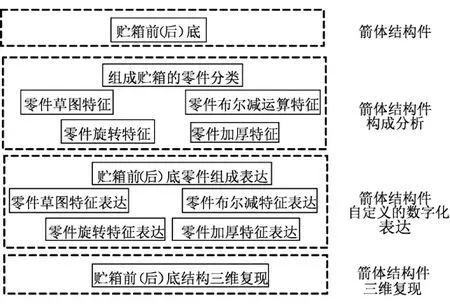
图2 贮箱前（后）底结构的自主表达流程Fig.2 Independent Describing Flow Chart of the Ellipsoid Bottom Structural

2 曲线统一表达的关键算法研究

2.1 任意椭圆弧段的NURBS 表示

贮箱前（后）底的横截面可以被划分为3 段椭圆弧，如图3 所示，从法兰盘开始，顺时针方向弧AB 为法兰瓜瓣连接环板的横截面椭圆弧、弧BC 为瓜瓣结构的横截面椭圆弧、弧CD 为叉形环的横截面椭圆弧。贮箱前（后）底的造型设计问题转变为已知椭圆上任意两点的位置坐标和椭圆的曲线方程，求解用NURBS表示的指定椭圆弧的参数曲线方程[3,4]。

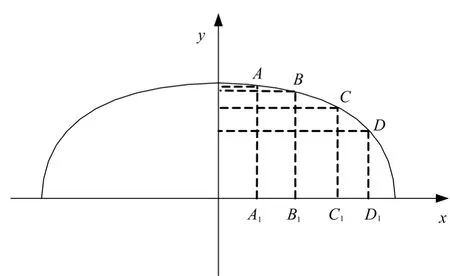
图3 椭圆形贮箱底横截面示意Fig.3 Cross Section of the Ellipse on the Tank Bottom

椭圆弧至少需要用3个控制点的二次曲线来表达，如图4 所示。

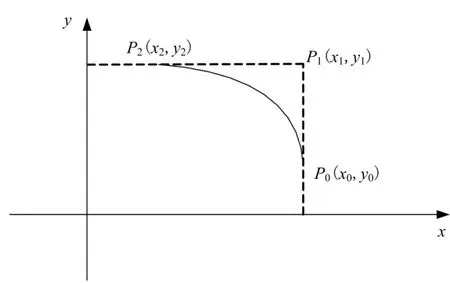
图4 椭圆弧的NURBS 曲线Fig.4 NURBS Express of the Elliptic Arc

取：

得到用3 个控制点表示的二次NURBS 曲线椭圆弧参数方程为

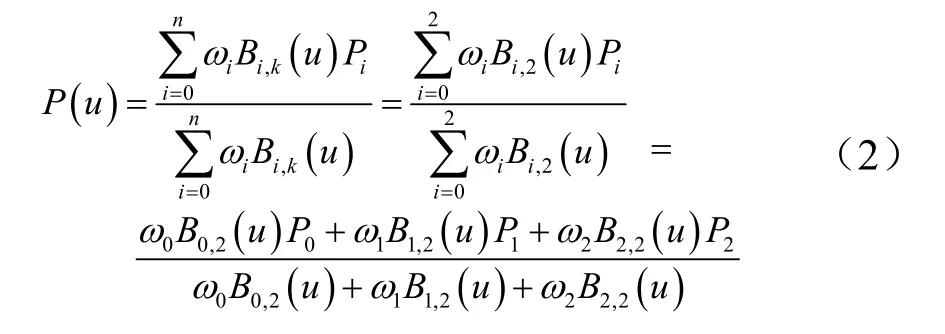
式中 ωi为控制顶点的权因子， i = 0,1,… ,n；n 为控制点个数的编号；Bi,k（ u ）为根据B 样条递推公式确定的k次规范B 样条基函数，共n+ 1个控制顶点的数量；k 为控制曲线的最高阶次；u 为结点矢量的控制参数。取：

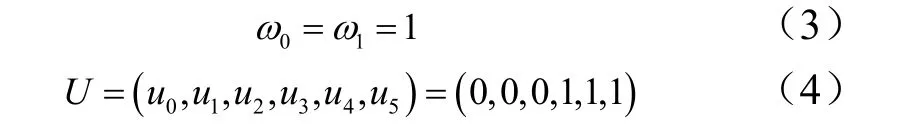
整理，得：

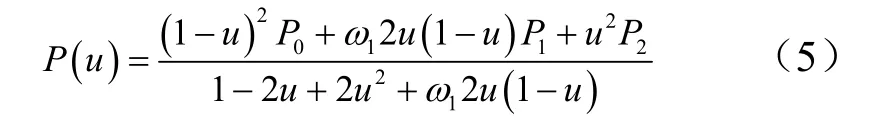
由此可解得1ω ，即得到用3 个控制点表示的二次椭圆弧的NURBS 参数曲线方程。

2.2 任意椭圆弧段经加厚特征后的NURBS 表示

任意段的椭圆弧经加厚特征后，需要准确找到椭圆弧端点沿椭圆弧径向平移一定距离的点的坐标，如图5 所示。

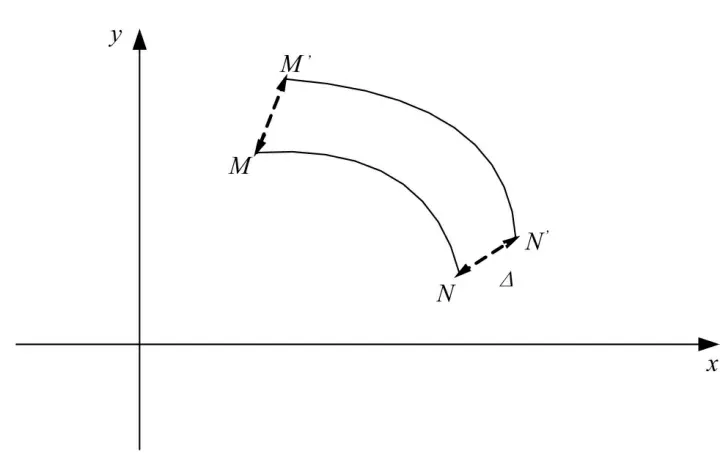
图5 任意段椭圆弧加厚特征后示意Fig.5 Schematic Diagram of the Thickened Arbitrary Elliptic Arc

点M 的坐标为（ xM,yM），点N 的坐标为（ xN,yN），椭圆弧MN 在点M 处的切线方程为

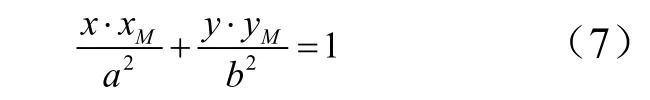
点M 处的法向量为

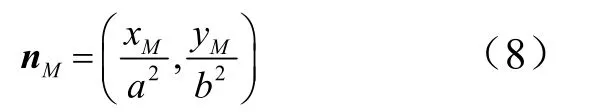
联立方程即可解得任意椭圆弧上一点沿径向平移Δ 距离之后的点的坐标和再按照2.1 节方法确定任意段椭圆弧加厚之后的NURBS 表示。

2.3 任意直线段的NURBS 表示

直线段的NURBS 表示可以用两个端点的一次曲线来表示，即令 n= 1， k= 1，则，

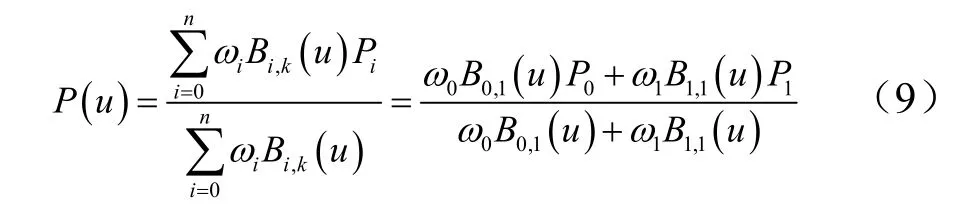
取 ω0= ω1= 1，令结点矢量：

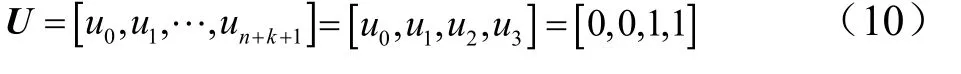
则，

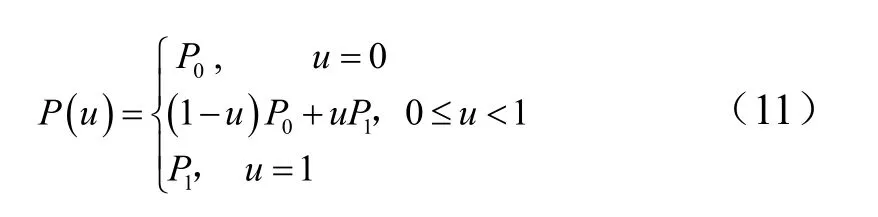
2.4 任意圆弧段的NURBS 表示

圆弧段的NURBS 表示可以用3 个端点的二次曲线来表示，即令 n= 2， k= 2，类似于任意椭圆弧段的NURBS 表示，令ω0= ω1= 1，可求得ω1，即得到用3 个控制点表示的二次圆弧的NURBS 参数曲线方程。

3 椭球形贮箱前（后）底结构三维模型

3.1 数字化表达

XML 语言具有准确表示结构化数据和半结构化数据的功能，且不依赖任何编程语言、操作系统或软件供应商，与平台无关，具有良好的扩展性[5]，故本文使用XML 完成贮箱典型结构的数字化统一表达，以下是对贮箱前底结构的XML 描述：

3.1.1 法兰的数字化表达

法兰结构是在草图特征的基础上经过旋转特征生成的。草图特征由直线段和圆弧段组成，直线段用两个端点的一次NURBS 曲线表示，即直线段的NURBS表示需要用到n、k 、0ω 、1ω 、 u0、1u 、 u2、 u3以及直线段两个端点的x、y、z 坐标值共14 个参数，如下所示：

............

............

圆弧段用3 个端点的二次NURBS 曲线表示，即圆弧段的NURBS 表示需要用到n、k 、0ω 、1ω 、2ω 、u0、 u1、 u2、 u3、 u4、 u5以及圆弧段的3 个控制顶点的x、y、z 坐标值共20 个参数，圆弧段关键参数的定义参考直线段，以参数n 为例的定义为

3.1.2 法兰瓜瓣连接环板的数字化表达

法兰瓜瓣连接环板结构是在草图特征的基础上经旋转特征和加厚特征生成。草图特征由椭圆弧段组成，本文用3 个端点的二次NURBS 曲线来表示椭圆弧曲线，即椭圆弧的NURBS 表示需要用到n、k、ω0、ω1、ω2、 u0、 u1、 u2、 u3、 u4、 u5，以及椭圆弧段的3 个控制顶点的x、y、z 坐标值共20 个参数，椭圆弧段关键参数的定义也可以参考直线段，以参数n 为例的定义如下：

3.1.3 瓜瓣的数字化表达

瓜瓣结构是在草图特征的基础上经旋转特征、加厚特征和布尔减运算特征生成的。草图特征由椭圆弧段组成，椭圆弧段的表示同法兰瓜瓣连接环板的椭圆弧表示，即每一段椭圆弧段都需要记录20 个参数。瓜瓣结构用到了布尔减运算，瓜瓣结构的布尔减运算是在一个大的椭圆弧板的基础上布尔减运算掉一个小的椭圆弧板，运算的XML 描述如下：

3.1.4 叉形环的数字化表达

叉形环结构是在草图特征基础上经旋转特征生成。类似于法兰，叉形环的草图特征由直线段和椭圆弧段组成。叉形环草图特征中直线段的NURBS 表示和椭圆弧段的NURBS 表示同法兰和法兰瓜瓣连接环板。

3.2 数字表达方式的可视化

本文使用开源的三维 CAD 几何造型引擎OpenCASCADE 来验证贮箱结构三维模型采用基于NURBS 的统一描述方法的可行性[6,7]。基于自定义的XML 描述文件，在OpenCASCADE 基础上开发了自动读取3.1 节中自定义的模型描述文件的接口，实现了自定义模型信息的三维模型可视化[8]。

借助开发的数据读取接口和OpenCASCADE 将

3.1.1 节中的法兰结构数字化表达实现可视化，如图6a所示。法兰结构的原Creo 三维模型如图6b 所示。

图6 法兰两种可视化三维模型比较Fig.6 Comparison of the Two Kinds of Falan Model

同理，法兰瓜瓣连接环板结构的数字化表达实现可视化，如图7a 所示，法兰瓜瓣连接环板结构的原Creo 三维模型图如图7b 所示。

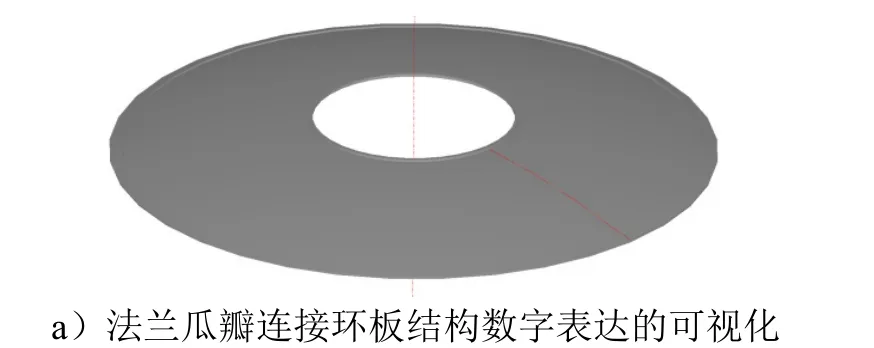
图7 法兰瓜瓣连接环板两种可视化三维模型比较Fig.7 Comparison of the Two Kinds of Falan and Melon Petals Collection Plate Model

续图7

同理，瓜瓣结构的数字化表达实现可视化，如图8a 所示，瓜瓣结构的原Creo 三维模型图如图8b 所示。

图8 瓜瓣结构两种可视化三维模型比较Fig.8 Comparison of the Two Kinds of Melon Petals Model

同理，叉形环结构的数字化表达实现可视化，如图9a 所示，叉形环结构的原Creo 三维模型图如图9b所示。

图9 叉形环结构两种可视化三维模型比较Fig.9 Comparison of the Two Kinds of Fork-like Ring Model

续图9

4 结 论

通过研究任意段曲线的NURBS 表示方法，将航天结构件的常用线段用统一的方式进行表达，提出了一种航天专用的结构件自主可控的数字表达及描述方法，以运载火箭的贮箱典型结构件为例，验证了运载火箭典型三维结构模型的自主化统一表达方法的可行性。验证实例结构较为简单，对于较复杂的结构可用类似的描述方法进行定义及三维复现，本文提出的描述方法为航天弹箭体结构件统一化表达的实现做好了技术储备，为后续自主定义及实现三维结构的可视化提供了参考。