兰州压实黄土水分迁移规律试验与数值模拟

李博鹏 胡海军 严武庆

摘 要：为了研究试坑浸水试验过程中水分迁移规律，依托兰州市填沟造地工程，首先对压实黄土进行一维入渗试验并应用改进的浸润锋前进法获得压实黄土的非饱和渗透系数函数;然后依据非饱和土体水分运动理论，应用SWMS-2D程序建立了室内试坑浸水的土体水分轴对称二维数值模型，利用该模型并应用求解Richard方程的数值方法，对可以清晰观测浸润锋的室内试坑浸水试验进行了模拟;最后对比了一维入渗和二维入渗的差别。结果表明：数值模拟法能较好地预测室内试坑浸水试验中的浸润锋迁移规律，说明应用一维土柱获得的非饱和渗透系数函数以及求Richard方程数值方法的可靠性;随着试坑直径的增大，试坑中心线下浸润锋迁移规律趋向于一维入渗;已有近似解析模型在预测试坑中心线下水分场变化规律是可靠的，数值计算方法能模拟水平入渗范围。

关键词：黄土;浸润锋;数值模拟;水分迁移

中图分类号：TU444;TV16 文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.12.031

Abstract：In order to study the law of water migration during the immersion test， this paper relied on the Lanzhou landfill project， firstly carried out onedimensional infiltration test in compacted loess and applied the improved wetting front forward method to obtain the unsaturated hydraulic conductivity function of compacted loess. Then based on the theory of unsaturated soil water movement， the SWMS2D program was used to establish the axisymmetric twodimensional numerical model of the indoor pit immersion test. Using the model and applying the numerical method of solving the Richard equation， indoor immersion test in which the wetting front could be clearly observed was simulated. Finally， the difference between onedimensional infiltration and twodimensional infiltration was compared. The research shows that the numerical simulation method can well predict the migration law of wetting front in the indoor pit immersion test. It proves that the unsaturated hydraulic conductivity function obtained by applying the onedimensional soil column and the numerical method of calculating the Richard equation are reliable. Numerical experiments show that with the increase of the diameter of the test， the migration law of the wetting front under the center line of pit tends to onedimensional infiltration. The approximate analytic model is reliable in the change of the water field under the center line of the pretest pit. The numerical simulation can well predict the wetted range in horizontal direction.

Key words： loess; wetting front; numerical simulation; water migration

隨着西部开发和国家“一带一路”倡议的实施，黄土高原地区的工程建设项目日益增多，如兰州市和延安市开展的“削山造城”工程建设[1]。这些工程涉及深厚重塑黄土填方，众所周知，非饱和黄土的力学特性具有水敏性，其强度和变形模量与含水率密切相关，在应力作用下遇水易发生湿陷变形，而黄土地基在浸水过程中是逐步增湿的[2]，研究人员已开始关注黄土单元体及黄土地基的增湿变形情况[3-5]，获得浸水过程中的水分场是研究黄土地基增湿变形的前提。对于黄土水分迁移试验研究，李萍等[6]设计人工滴水试验模拟天然降雨条件，研究了黄土地区降雨入渗地面水分的迁移;朱才辉等[7]以西北地区黄土高填方工程为研究背景，开展了不同压实度下重塑黄土在小雨、中雨和大雨情况下的水分迁移规律研究;刘保健等[8-10]开展了现场浸水试验，研究了原状黄土水分入渗规律。对于一维入渗，应用Green-Ampt模型以及修正Green-Ampt模型[11-12]计算水分迁移过程已有大量研究。对于二维以及三维入渗，求解Richard方程的数值方法[13-16]以及近似解析解[17-19]得到广泛应用，池宝亮等[13]应用求解Richard方程的Hydrus软件建立了点源滴灌的土壤水分轴对称二维数值模拟模型，分析了几种土壤条件下地埋点源滴灌时土壤水分的运动状况;李道西等[14]利用Hydrus软件对不同地下滴灌系统设计参数下土壤水分分布进行了模拟分析;王铁行等[15-16]应用自编程序分析了降雨条件下非饱和黄土路基水分场的变化等;张爱军等[5]应用GeoStudio软件分析了不同防渗层下渠基浸水的水分场变化;穆斯塔伐耶夫[17]利用近似解析法得到了浸水过程中二维解析解;刘保健等[18]根据黄土浸水试验的量测结果，提出了黄土的二维入渗模型。

笔者依托兰州市填沟造地工程，对压实黄土进行一维入渗试验，应用改进的浸润锋前进法[19]获得了压实黄土的非饱和渗透系数函数，然后应用求解Richard方程的数值方法，对可以清晰观测到浸润锋的室内试坑浸水试验进行了模拟，并对比了一维入渗和二维入渗的差别，分析了已有近似解析解的可靠性。需要说明的是，室内试坑浸水试验能克服现场试验[20-22]观测浸润锋的误差，但受室内模型的限制，入渗过程中的湿陷变形对渗透参数的影响在研究中暂不考虑。

1 土体情况及非饱和渗透参数

1.1 试验土体

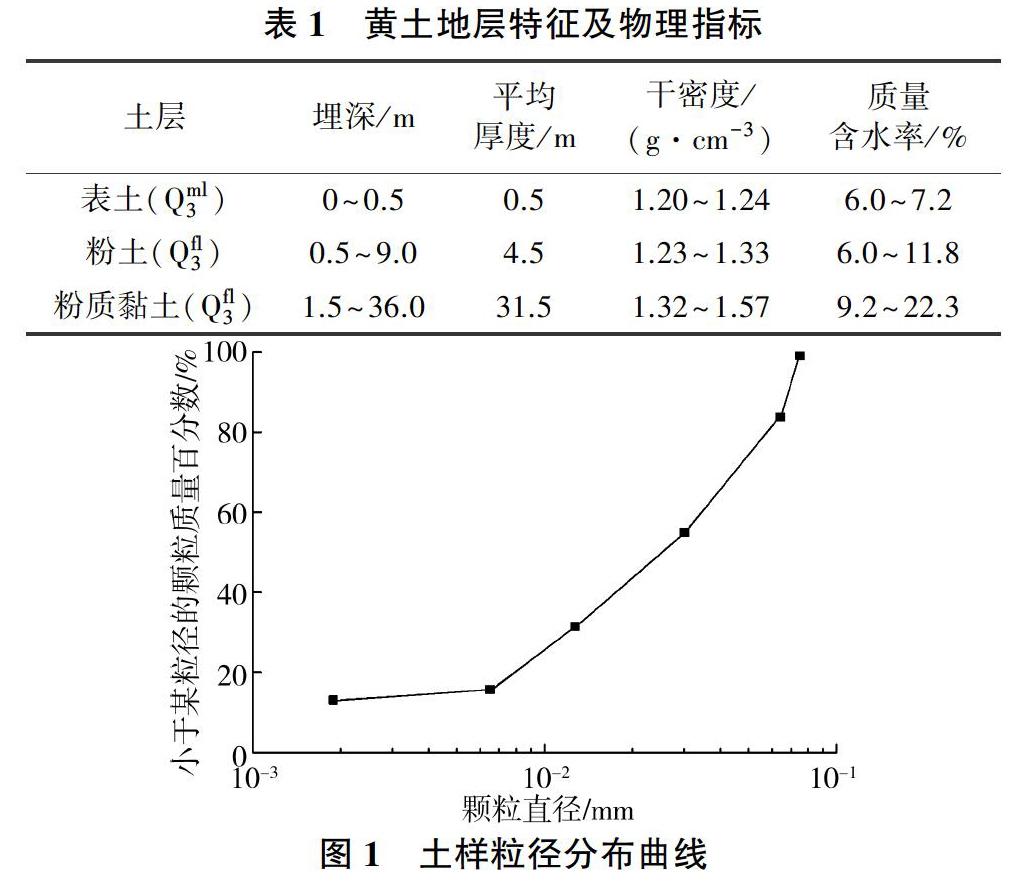
试验所用黄土取自蘭州市和平镇金川科技园，地貌单元属黄河南岸Ⅳ级阶地。取样场地为厚度36.5 m的Q3黄土，湿陷程度强烈。场地各土层物理指标见表1[21]，取样土层为粉土层，埋深为0.5～9.0 m;土样干密度为1.23～1.33 g/cm3，颗粒级配见图1。

1.2 渗透参数的测定

1.2.1 一维土柱制取

有些填沟造地工程填方区存在黄土压实度很低的情况[23-24]，如延安新区压实后孔隙比接近1.15[23]，这种状态和天然状态孔隙比接近，因此在研究压实黄土水分迁移规律时，笔者选用了与原状黄土相近的孔隙比，制样土料质量含水率为8.9%，土柱直径为 14 cm，考虑已有一维入渗试验土柱长度与直径比通常大于5[25]，土柱长度采用90 cm。土柱共分18层、每层5 cm，击实而成，制样时根据目标孔隙比和土料含水率计算每层土料的质量，每层击到目标高度后均刮毛后再填装一层土料。整个试验装置主体为竖直放置的有机玻璃管，总长1 m，顶端设置1.8 cm高的恒定水头。考虑到张力计有滞后效应，入渗试验仅应用ECH20水分仪（脚长约5 cm）测定各测点体积含水率，而基质吸力依据持水曲线计算得到，水分仪以15 cm等间距布置，共布设5个水分仪，从上往下距离土柱顶部分别为15、30、45、60、75 cm，依次命名为测点A、B、C、D、E。有机玻璃管上水分仪的孔为长条形孔，制土柱时先将这些孔用塞子塞住，以防止制样时土从孔中漏出，当制样高度大于传感器高度时，将塞子取出，插入水分仪，并用橡皮泥密封水分仪与有机玻璃管间隙。马氏瓶用于提供与土柱最高点相同的恒定水位并用于获得入渗量信息。

1.2.2 持水曲线测试

该试验所用仪器见图2，水分仪需要标定校正，先配置质量含水率为8.9%的土料、静置1 d后进行含水率测试，在直径为10 cm高度为10 cm的有机玻璃管中按干密度为1.28 g/cm3制样，5 cm一层，制作两层，共制作6个试样。对6个试样分别加水至质量含水率为12%、16%、20%、24%、28%、32%。在试样中，沿着玻璃管圆周分布插入所有水分仪，各水分仪一般读数相差不大，如相差太大，证明没插紧或水分仪脚没完全插入;之后记录读数，然后挖出一定量的土测试含水率。应用浸润锋前进法确定非饱和渗透系数时，需要一维入渗过程中各测点的基质吸力变化，这需要根据土水特征曲线计算得到。因此，对土水特征曲线进行了测试，埋入土壤MPS-6水势传感器测试6个试样的基质吸力。对于低吸力情况，埋入张力计复测，稳定后再次测定土体含水率。

应用土壤水势传感器法和张力计法可测得吸力和体积含水率关系的离散点（见图3）。应用式（1a）VG模型[26]对测试离散点进行拟合，所得参数见图3。

式中：θ为体积含水率;θs为土样饱和体积含水率，这里采用浸水到饱和的实际体积含水率0.47;θr为残余含水率，根据数据拟合获得;ψ为基质吸力，kPa;a为与进气值有关的拟合参数，kPa;n为与曲线斜率有关的拟合参数;m=1-1/n。

1.2.3 一维入渗试验及非饱和渗透系数函数的确定

应用水分仪读数与实际体积含水率之间的标定关系，获得一维入渗试验过程中各测点体积含水率随时间的变化情况，见图4。

采用改进的浸润锋前进法获得非饱和渗透系数函数，具体过程如下：根据土柱上各测点含水率开始变化的时间即浸润锋达到该处的时间与在试验过程观测记录的浸润锋位置与时间的数据点，得到浸润锋迁移距离与时间的关系（见图5）;

应用zf=2.37t0.553 2很容易得到不同时刻浸润锋迁移速率vzf，以其中一个测点A为例，按式（2a）计算得到t1—t2时间段通过A断面水的平均流速v（zA，t1+t22）;依据浸润锋前进法[27]，采用式（2b）计算t2时刻A断面的水力梯度i（zA，t2）;依据改进的浸润锋前进法[19]，采用式（2c）计算t1—t2时间段A断面的平均水力梯度i（zA，t1+t22）;根据达西定律便可得到该时间段平均吸力下的渗透系数。选取不同的时间段便可得到不同吸力下的渗透系数：

图6给出了应用改进的浸润锋前进法所得不同吸力下的非饱和渗透系数。应用VG模型对所得非饱和渗透系数和基质吸力的关系进行拟合（E点浸润锋达到底边界，浸润锋前进法的假设不成立），这里便没用测点E获得非饱和渗透系数。笔者采用邵明安等[28]的建议，将入渗试验后的土柱进行渗透试验，通过马氏瓶读数与时间的关系获得土体饱和渗透系数ks=2.74×10-4 cm/s。由于应用式（1b）与式（1c）拟合非饱和渗透系数时，所得a和n与原持水曲线拟合参数不同，因此需要在新的a和n条件下，重新拟合土水特征曲线，得到残余含水率θr为0.048 2，通过对比测试点发现前后两次所得持水特征曲线在增湿区间都很接近测试点，而入渗过程是增湿过程，所得非饱和渗透系数函数在含水率大于初始含水率时具有足够的精度。

2 室内试坑浸水试验

模型试验利用一上部开口的有机玻璃容器作为模型箱，在该模型箱中制取40 cm×40 cm×40 cm土样。为在有机玻璃容器两侧可以清晰地看到浸水过程，在土样顶部平面4个角中选一个角，以角顶点为圆心，以5 cm为半径，形成一个四分之一的圆，向下挖取5 cm试坑，并置入半径为5 cm的1/4有机玻璃管作为护壁，在试坑中填入3 cm高的大粒径石子。试验开始时向四分之一的圆柱试坑中加入5 cm高水头，并且加水后试坑由橡胶管连接马氏瓶以维持试坑中水头不变，模拟实际场地的浸水试坑试验。土体在分层制样过程中埋设水分仪，从而获得浸水过程中不同位置地基土的水分变化。在水分入渗过程中，通过试坑两侧有机玻璃面观察入渗情况，并用记号笔每隔一段时间画出浸润锋的位置，见图7。

3 數值计算

3.1 土体水分运动方程

根据达西定律和质量守恒原理，浸水试坑下的土体水分运动一般属于三维问题。若假定土体为各向同性的均质体，本文所研究圆形试坑浸水下的水分运动具有轴对称性，可视为轴对称条件下的二维问题，其土体水分运动方程为

3.2 初始条件

3.3 边界条件

均质土体浸水试坑的土体水分运动可视为轴对称条件下的二维问题，由于轴对称性，因此仅研究水分运动剖面的一半即可。利用Galerkin有限单元法完成对数学模型的数值求解[29]。将模拟计算区域剖分为矩形单元，边界条件见图8，室内试验中试坑侧壁用了有机玻璃管，所以设置为不透水边界。

4 水分迁移过程数值模拟结果

4.1 水分场计算结果

上述室内试坑浸水模型试验，由于具有轴对称性，可视为轴对称条件下的二维问题，运用上述建立的数学模型并利用SWMS-2D程序对室内试坑数值模型试验进行模拟，并用Surfer软件绘制出水分场并与模型箱试验浸水过程中实际观测记录的10、30、90、270、510、630 min浸润锋位置进行对比，见图9。

由图9可见，利用笔者所建立的模型所得不同时刻浸润锋位置与实测浸润锋位置两者具有较好的一致性，水平方向在270 min之后出现些许差异，实测浸润锋水平前进速度要比预测速度慢，可能是试验时上部边界未用保鲜膜覆盖导致有一定的蒸发造成的。

4.2 浸润锋迁移规律一维与二维差别分析

为分析一维入渗与试坑入渗的差异，对两种试坑直径下浸润锋深度与时间的关系与一维入渗试验结果进行对比，见图10。由图10可以发现，随着试坑直径的增大，试坑中心线下浸润锋迁移规律偏向于一维入渗，浸润锋深度较小时更符合一维入渗。

4.3 已有试坑中心线下水分分布计算模型可靠性验证

为验证已有解析模型在预测水分场变化规律上的可靠性，利用式（6a）拟合浸润锋迁移规律，见图11。然后用式（6b）计算得到试坑中心线下含水率沿深度的分布及随时间变化的规律。

5 结 论

笔者依托兰州市填沟造地工程，对压实黄土进行了一维入渗试验，应用改进的浸润锋前进法获得压实黄土的非饱和渗透系数函数，然后应用求解Richard方程的数值方法，对可以清晰观测浸润锋的室内试坑浸水试验进行了模拟，并对比了一维入渗和二维入渗的差别，分析了已有近似解的可靠性，得出如下结论：

（1）数值模拟结果能较好地预测室内试坑浸水试验中的浸润锋，说明应用一维土柱获得的非饱和渗透系数函数以及求解Richard方程数值方法的可靠性。

（2）分析一维入渗与二维试坑入渗的差异，发现随着试坑直径的增大，试坑中心线下浸润锋迁移规律趋向于一维入渗，且浸润锋深度较小时更符合一维入渗。

（3）已有近似解析模型在预测试坑中心线下水分场变化规律是可靠的，数值计算方法能模拟水平入渗范围。

综上，笔者所建模型能比较真实地反映试验土体二维入渗条件下的水分迁移运动情况。

参考文献：

[1] LI P， QIAN H， WU J H. Environment： Accelerate Research on Land Creation[J]. Nature， 2014， 510：29-31.

[2] 建工部建筑科学研究院地基砖木研究室.西安黄土地基浸水后变形范围的试验研究[J].建筑学报，1961（3）：21-27.

[3] 张苏民，郑建国.湿陷性黄土（Q3）的增湿变形特征[J].岩土工程学报，1990，12（4）：21-31.

[4] 付艳斌，王铁行，赵树德，等.黄土地基水分入渗分析及增湿变形计算[J].西安建筑科技大学学报（自然科学版），2005，37（2）：210-214.

[5] 张爱军，邢义川，汪海涛，等.基于增湿变形的渠道工程黄土渠基湿陷性评价方法[J].水利学报，2017，48（1）：41-51，60.

[6] 李萍，李同录，王阿丹，等.黄土中水分迁移规律现场试验研究[J].岩土力学，2013，34（5）：1331-1339.

[7] 朱才辉，张世斌.降雨条件下压实黄土水分入渗规律模型试验研究[J].岩土工程学报，2018，40（6）：1117-1124.

[8] 刘保健，谢永利，于友成.黄土非饱和入渗规律原位试验研究[J].岩石力学与工程学报，2004，23（24）：4156-4160.

[9] 黄雪峰，陈正汉，哈双，等.大厚度自重湿陷性黄土场地湿陷变形特征的大型现场浸水试验研究[J].岩土工程学报，2006，28（3）：382-389.

[10] 姚志华，黄雪峰，陈正汉，等.兰州地区大厚度自重湿陷性黄土场地浸水试验综合观测研究[J].岩土工程学报，2012，34（1）：65-74.

[11] MEIN R G， FARRELL D A. Determination of Wetting Front Suction in the Green-Ampt Equation [J]. Soil Science Society of America Proceedings， 1974， 38（4）： 872-875.

[12] MA Y， FENG S Y， SU D Y， et al. Modeling Water Infiltration in a Large Layered Soil Column with a Modified Green-Ampt Model and HYDRUS-1D [J]. Computers and Electronics in Agriculture， 2010， 71（S）： 40-47.

[13] 池宝亮，黄学芳，张冬梅.点源地下滴灌土壤水分运动数值模拟及验证[J].农业工程学报，2005，21（3）：56-59.

[14] 李道西，彭世彰.地下滴灌灌水设计参数对土壤水分分布影响的计算机模拟[J].沈阳农业大学学报，2004，35（增刊1）：507-509.

[15] 王铁行.非饱和黄土路基水分场的数值分析[J].岩土工程学报，2008，30（1）：41-45.

[16] 王铁行，罗扬，任海波.管沟渗水下的黄土地基水分场数值分析[J].地下空间与工程学报，2011，7（1）：54-58，111.

[17] 穆斯塔伐耶夫.湿陷性黄土上地基与基础的计算[M].北京：水利电力出版社，1984：67-119.

[18] 刘保健，谢定义，郭增玉.黄土地基增湿变形的实用算法[J].岩土力学，2004，25（2）：270-274.

[19] 胡海军，李常花，崔玉军，等.增湿情况重塑黄土非饱和渗透系数的测定方法研究[J].水利学报，2018，49（10）：1216-1226.

[20] 苏立海，姚志华，黄雪峰，等.自重湿陷性黄土场地的水分运移规律研究[J].岩石力学与工程学报，2016，35（增刊2）：4328-4336.

[21] 姚志华.大厚度自重湿陷性黄土的水气运移和力学特性及地基湿陷变形规律研究[D].重庆：后勤工程学院，2012：45-87.

[22] 米维军，熊治文，屈耀辉，等.郑西铁路客运专线路基防排水技术研究[J].铁道工程学报，2010，27（5）：4-8.

[23] 张沛然.沟谷填方非饱和黄土填料增减湿变形特性、模型及结构性分析研究[D].兰州：兰州理工大学，2018： 22-26.

[24] 李金奎，陶韬，吴凯.灰土桩处理高填方湿陷性黄土管廊地基的试验研究[J].四川建筑科学研究，2018，44（5）： 59-63.

[25] NG C W W， LEUNG A K. Measurements of Drying and Wetting Permeability Functions Using a New Stress-Controllable Soil Column[J]. Journal of Geotechnical and Geoenvironmental Engineering， 2012， 138（1）： 58-68.

[26] VAN GENUCHTEN M T. A ClosedForm Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils [J]. Soil Science Society of American Journal， 1980， 44（5）： 892-898.

[27] LI X， ZHANG L M， FREDLUND D C. Wetting Front Advancing Column Test for Measuring Unsaturated Hydraulic Conductivity[J].Canadian Geotechnical Journal， 2009， 46（12）： 1431-1445.

[28] 邵明安，王全九，HORTON R.推求土壤水分運动参数的简单入渗法：Ⅱ实验验证[J].土壤学报，2000，37（2）：217-224.

[29] SIMUNEK J， SEJNA M， VAN GENUCHTEN M T. The HYDRUS-2D Software Package for Simulating the TwoDimensional Movement of Water， Heat， and Multiple Solutes in Variably Saturated Media[M]. California： U.S. Department of Agriculture， 1999： 57-62.

【责任编辑 赵宏伟】