基于神经网络和遗传算法的泥沙模型研发及应用

2020-12-30陈雄波王俊昀龚钰婷

人民黄河 2020年12期

陈雄波王俊昀龚钰婷

摘要：针对黄河流域的泥沙问题，根据BP网络原理和训练流程、遗传算法原理，优化BP网络参数的加速遗传算法的迭代步骤，编制了计算程序;根据数学模型计算及管理的特点，设计完成了软件功能表和模型功能模块;在研发的软件中检验了计算程序模块的功能，经测试是正确的;将计算模块无缝嵌入到模型软件中，并通过方案管理、结果查询等辅助模块实现了计算过程的通用化、可视化。该模型软件的组成模块在黄河口流路运用方案比选、多泥沙河流断面概化中得到应用，经分析成果比较合理。

关键词：BP神经网络;遗传算法;优化模型;计算过程;通用化;可视化

中图分类号：TP183;TV142;TV882.1 文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.12.004

Abstract：Aiming at the sediment problem in the Yellow River basin， according to the principle of BP network and training flow， genetic algorithm and the iteration steps of accelerated genetic algorithm to optimize the parameters of BP network， and the calculation program was compiled. According to the characteristics of mathematical model calculation and management， the software function table and model function module were designed and completed. The calculation program was tested and verified. The calculation module was seamlessly embedded in the model software and the computational process was universal and visualized through auxiliary modules such as scheme management and result query. The component module of the model software had been applied in the comparison and selection of the operation schemes of the Yellow River estuary and the generalization of the sedimentladen river section. The analysis results were reasonable.

Key words： BP neural network; genetic algorithm; optimization model; computational process; general utilization; visualization

1 神經网络和遗传算法原理

描述水沙运动的N-S方程、对流-扩散方程都是非线性的。近年来，各种非线性数学方法在泥沙研究领域有了很多应用，如人工神经网络（Artificial Neural Network，简称ANN）和遗传算法（Genetic Algorithm，简称GA）等。

Trent等首次将ANN应用于泥沙运动规律研究，实际应用的神经网络模型大都采用误差逆传播（BackPropagation，简称BP）网络及其变化形式。典型的BP网络包含输入层、中间层（也称隐含层）和输出层，各层之间实行全连接。BP网络的学习训练由4个过程组成，即模式顺传播、误差逆传播、记忆训练和学习收敛[1]。

GA的算法如下：①用二进制数字串来模拟染色体，用数字串中的某位元模拟基因，用数量极大的数字串表示优化问题可行域内的试探解;②用目标函数或其变化形式作为适应度函数来模拟个体对生存环境的适应性;③对适应度较高的数字串进行杂交，得到下一代（子代）;④子代数字串变异;⑤进化迭代，转步骤②，如此反复运行，直至获得满意的解或达到预定进化迭代次数，并把适应度最高的数字串所表示的解作为优化的结果。遗传算法是在“优胜劣汰”指导下的随机并行自适应优化方法，可视为介于确定性与随机性优化方法之间的一类新的优化方法[2]。

2 基于神经网络和遗传算法的泥沙模型和软件功能设计

目前所使用的泥沙计算模型大都人为依赖度高、更新困难、可视化差，且缺乏先进、科学的优化方法。通过对非线性数学优化方法的应用研究，针对黄河流域的泥沙问题，结合实际工作需要和现有经验模型的优点，研发出一套泥沙模型软件，并以应用模块、模型系统的形式提交出来，实现模型运算的通用化、可视化、软件化。

2.1 基于神经网络的泥沙模型建立步骤

基于神经网络的泥沙模型建立步骤如下：①根据河流动力学理论，选择输入、输出因子，以多泥沙河流为例，把汛期冲淤量作为输出因子（因变量），与上游控制站来水量和来沙量、区间汇流或引水产生的来水来沙量、洪峰过程（可通过流量分级来表达）等有关，这些物理量作为输入因子（自变量）;②输入、输出因子的归一化工作，即将所有变量通过一定的变换转化到0～1之间;③编制BP网络训练和预测程序，在达到指定迭代次数并且全局误差小于一定值后，训练迭代停止;④保存连接权值及阈值，输出训练值;⑤采用新的输入因子，根据BP网络的连接权值及阈值，可得到预测值。

2.2 基于遗传算法的泥沙模型建立步骤

基于遗传算法的泥沙模型建立步骤如下：①根据河道治理实践，建立经验公式，假定河流进口断面流量Q上、出口断面含沙量S下、河道比降J是决定河道输沙率QS的相关因素，建立QS与Q上、S下、J之间的经验关系，可能有直线形式、指数形式、对数形式、三角函数或其组合等;②将经验公式涉及的自变量、因变量整理、输入到模型软件中;③设定优化函数;④采用遗传算法优化经验公式中的参数，使计算值与实测值差别（优化函数残差）震荡减小;⑤在达到指定迭代次数并且优化函数残差小于一定值后，保存经验公式中的参数，输入新的自变量组次，采用该公式可得到预测值。

2.3 模型软件功能设计

考虑基于神经网络和遗传算法的泥沙模型软件的计算及管理特点，该模型软件功能见表1。

3 模型软件开发及计算过程的通用化、可视化

3.1 软件登录

系统主界面按照功能区域可分为3个部分：一是系统主菜单区，包括模型计算、方案管理、统计报表、数据图表、动态显示和结果查询6个主要功能按钮;二是功能子菜单区，根据系统主要功能的选择不同显示相对应的详细操作功能;三是地图平面显示区，由黄河流域水系GIS地图构成，并将各计算模型布置在GIS图形对应水库位置上，便于用户直观地点击计算模型和进行主要参数的查询。

3.2 模型计算

进入软件主界面后，点击“模型计算”按钮，进入模型计算界面。“模型计算”主界面包括方案选择的相关信息、运用方式选择、水沙系列选择、起始年份与计算年数、创建时间与创建用户、方案说明等。

模型计算是软件研发中最为核心的功能模块，承担着计算前处理、模型计算过程控制、模型计算后处理、模型计算进度、计算中间过程数据的显示分析以及神经网络与遗传算法相结合的多模型联合计算控制等重要功能的实现。主要功能模块如下。

（1）分组统计模块。

流量是影响河道冲淤能力的关键参数之一，发电量、引水供水量、输沙能力、河道糙率计算等都与流量有关，因此分组流量统计是一项非常常见的工作，对长系列而言，如果用常规方法统计，工作十分繁琐。在该模块中填写左侧相关分析数据并准备好基于Excel表格的数据后，点击“开始统计”按钮，分流量级统计数据即在屏幕右侧显示。

该模块除了应用于流量分组统计以外，还可以应用于其他任何同类物理量（如降雨量、含沙量、集水面积等）的分组统计，只要将待分组的数据按照输入格式整理，点击相应按钮即可迅速获得结果，大大提高了工作效率。

（2）BP网络训练和预测模块。点击BP网络训练按钮可进行相应BP网络训练与预测，以参考文献[3]所列数据为例，输入黄河干流下河沿水文站水量、沙量、区间水沙量，各流量级出现天数由分组统计模型得出，以宁蒙河段1953—1999年（水文年）实测淤积量作为训练系列，2000—2004年作为预测系列，累计冲淤量训练（或预测）结果与实测值进行对比验证，结果比较合理[3]。

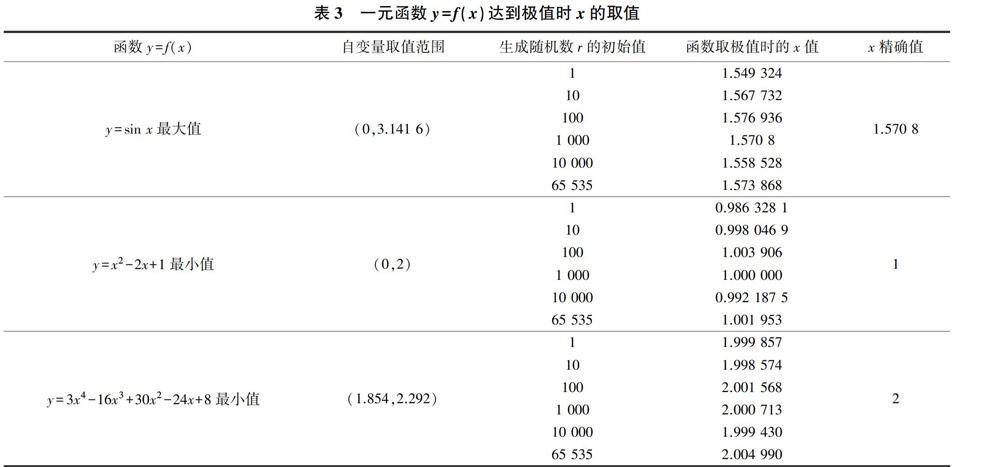
（3）遗传算法应用模块。选择遗传算法应用模块，在左侧菜单栏填入对应数据、函数或参数，点击“开始计算”按钮，按遗传算法规则进行一元函数计算，输出结果见表3。由表3可知，计算值与精确值十分接近，表明应用模塊测试正确。

（4）BP网络与遗传算法的结合模块测试。BP网络的参数包括连接权值及阈值，所谓BP网络的参数优化问题是指通过迭代改进这些参数，使网络全局误差更小。在BP算法训练网络出现收敛速度缓慢时启用GA来优化网络参数，把GA的优化结果作为BP算法的初始值再用BP算法训练网络，如此交替运行BP算法和GA就可加快网络的收敛速度，同时在一定程度上改善局部最小问题。这样交替利用BP算法和GA来训练人工神经网络的方法，称之为BP-GA混合算法。该算法包括如下8步：①BP网络的自变量参数变化区间的构造;②BP网络的参数的编码;③初始父代的生成;④父代个体的适应能力评价;⑤父代个体的选择;⑥父代个体的杂交;⑦子代个体的变异;⑧进化迭代[4]。

本次软件开发时嵌入BP-GA混合算法模块，采用参考文献[5]所列37组水槽试验挟沙力数据，分别用BP网络方法和BP-GA算法进行网络训练，结果表明：将初始连接权和阈值优化后，归一化后37组数据的综合误差由9.92×10-3下降为6.37×10-3，也就是说，BP-GA优化参数后，误差下降了35.8%，分散度减小，说明BP网络与遗传算法的结合模块通过了测试[5]。

在几个核心计算模块开发完成并成功通过测试后，将它们无缝嵌入到模型软件中，通过方案管理、结果查询等辅助模块，实现计算过程的通用化和可视化。

3.3 方案管理

方案管理功能子菜单包含了创建方案、删除方案、打开方案、方案对比、关闭方案5个功能操作按钮，并可以通过方案名称、创建人、创建日期等信息进行查询。其中方案对比提供了对系统数据库内所有已建方案模型计算结果的比对功能，通过选定任意个数的方案名称，即可对全河各个库区的模型计算结果按数据类型、系列年份进行分类比选，结果以图表形式直观地显示，同时支持显示结果的导出功能。

3.4 结果查询

该模块提供了丰富的模型计算结果数据分析手段和显示方式，模块基于Tee Chart Pro V5和MSH Flex Grid 6.0两大功能组件进行了二次开发，实现了图表、报表、动态显示相结合的结果显示分析手段。

通过与GIS综合显示分析相结合，用户可以直接在相应地形图上选择所要计算及训练的河段泥沙相关信息，系统将自动识别当前所选河道、水库的名称、类型以及所对应的数学模型信息，同时在GIS地图上以浮动窗口的形式显示该数学模型的所有计算结果类型供用户选择查询。

结果查询模块支持流量、输沙率、含沙量、冲淤量、水库蓄水量、水位等数据类型的查询，选择计算结果年份范围、数据类型后点击查询按钮，显示查询结果数据表，模型结果显示分析包含的统计报表、数据图表和动态显示等内容都穿插在各个模块中。

4 模型应用之一——黄河口流路运用方案比选

黄河入海口位于渤海湾和莱州湾之间，现行清水沟流路于1976年5月开始行河，改汊流路有3条，即现行清8汊河、北汊、1996年改汊前的河道。刁口河是1964—1976年行河的老河道，是黄河河口综合治理规划的备用流路。

4.1 清水沟、刁口河联合运用方案

入海流路改道控制条件：黄河河口发生10 000 m3/s洪水时西河口水位不超过12 m（大沽高程，下同）。清水沟计算初始条件为2017年汛前地形，刁口河采用过流能力3 000 m3/s的主河槽开挖后的地形，对两流路联合运用方案进行简要说明，见表4[6]。

4.2 评价指标及计算值

黄河口泥沙处置4个评价准则为技术、经济、生态、社会，包括11個指标，见表5。

4.3 评价结果

在评价指标中，数值最大为“优”的有平滩流量、外海输沙量、经济效益、供水保证率、生态流量保证率、湿地供水天数、代表性物种数量;数值最小为“优”的有淤积量经济投入、迁移人口、海岸侵蚀。选择各指标最优的为第一行，各指标平均值为第二行，各指标最差的为第三行，建立评价矩阵：

将矩阵（1）处理成数值均为0.05～0.95之间的输入文件，认为输出因子为矩阵（2），使用本次“基于神经网络和遗传算法的泥沙模型”BP网络模块训练20万次，全局误差E=2.31×10-4，说明训练效果较好。以第1～6方案的各指标数值作为输入值，使用BP网络预测模块，可得到输出值分别为0.41、0.61、0.44、0.71、0.33、0.51。

由于方案4得到的输出值0.71为各方案中的最大值，因此将方案4作为清水沟、刁口河联合运用的推荐方案。这与文献[6]结论一致，说明成果比较可靠。

5 模型应用之二——多泥沙河流断面概化

令m为实测资料总组数，采用“基于神经网络和遗传算法的泥沙模型”软件中的遗传算法模块来优化式（5）的参数ci，使优化函数的E极小化。

南京水利科学研究院在室内大型水槽中对多泥沙河流断面形态进行了试验研究，共进行了11组[1]。表7列出了本次GA算法和多元线性回归法的计算结果。

采用北洛河朝邑站1970年7月—1973年10月共24组实测数据[1]对本软件中GA算法的适用性进行检验，结果见表8。

从表7和表8可以看出，在大多数情况下，采用GA法得到的E比多元线性回归法略小，小部分比多元线性回归法稍大，说明采用本模型软件中遗传算法模块研究多沙河流断面概化是成功的。

6 结语

针对黄河泥沙问题，结合实际工作需要和现有经验模型的优点，对BP神经网络和遗传算法这两类非线性数学优化方法进行研究，通过改善现有多泥沙河流的经验计算方法，提高模型结果准确度和工作效率，建立了一套适用面宽、准确性较高、易修改的数学模型，可方便地应用于黄河泥沙问题规划研究实际工作中，主要结论如下。

（1）综合“基于神经网络和遗传算法的泥沙模型软件”的计算及管理的特点，设计完成了软件功能表和模型功能模块。

（2）根据BP网络原理和训练流程、遗传算法原理，优化BP网络参数的加速遗传算法过程，编制了计算程序，并在研发的软件中测试正确;将计算模块无缝嵌入到模型软件中，通过方案管理、结果查询等辅助模块，实现了计算过程的通用化和可视化。

（3）本模型软件的组成模块在黄河口流路运用方案比选、多泥沙河流断面概化中得到应用，经分析成果比较合理。

参考文献：