基于AHP-可拓理论的消落带岩质边坡稳定性分析

程平 王林峰 曾韬睿

摘 要：基于层次分析法（AHP）的可拓理论，以单轴抗压强度、岩体质量指标、变形模量、岩体透水系数、地下水发育程度、日最大降雨量、消落带水位变化、岩体结构面特征、黏聚力、内摩擦角10个因素为预测指标，采用层次分析法计算影响边坡稳定性的各个指标权重，在物元理论、可拓集合论和关联函数运算的基础上建立了三峡库区消落带岩质边坡稳定性分析的物元模型。通过对重庆巫山箭穿洞岩质边坡T1j1、T1d4、T1d3三段进行稳定性评价，发现T1j1属于Ⅰ级（稳定），T1d4和T1d3属于Ⅳ级（欠稳定），需要对基座和危岩进行加固处理，得出的结论与工程实际相符合。研究结果表明：基于层次分析法的可拓理论能较好地确定消落带岩体稳定性评价指标的权系数和反映其稳定性等级，可应用于消落带岩质边坡稳定性分析。

关键词：层次分析法;可拓学理论;消落带;岩质边坡;稳定性

中图分类号：TU457;TV697.1 文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.12.028

Abstract：This paper adopted extension theory based on Analytic Hierarchy Process （AHP） and considered 10 predictive indicators including uniaxial compressive strength， rock quality designation， deformation modulus， rock permeability coefficient， groundwater development degree， daily maximum rainfall， water level change in the hydrofluctuation belt， characteristic of rock structure plane，cohesion and internal friction angle. The weights of each index affecting slope stability were calculated by analytic hierarchy process. On the basis of matterelement theory， theory of extension set and correlation function operation， a matterelement model for stability analysis of rock slope in the Three Gorges Reservoir area was established. Through the stability evaluation of the three sections T1j1， T1d4 and T1d3 of the Wushan Jianchuandong rock slope in Chongqing， it was found that T1j1 belonged to level I and was in a stable state. T1d4 and T1d3 belonged to level IV and were in an unstable state， the pedestal and dangerous rock needed to be reinforced， and the conclusions obtained were consistent with the actual situation on site. The results show that the extension theory based on analytic hierarchy process can better determine the weight coefficient of the stability evaluation index of the rock mass in the hydrofluctuation belt and reflect its stability grade. This method can be applied to analyze the stability of rock slope in the hydrofluctuation belt.

Key words： stratification analysis method; extenics theory; hydrofluctuation belt; rock slope; stability

三峽水库自建成以来，根据防洪、发电等要求，水位出现周期性变化，改变了库区边坡的水文地质条件，滑坡等地质灾害发生的风险明显增大[1-3]，库区成为滑坡地质灾害高发区和重灾区，这些地质灾害严重影响航道的地质安全。因此，研究三峡库区消落带岩质边坡的稳定性具有十分重要的意义。

分析岩质边坡稳定性的方法有很多，常用的有模糊数学法[4-5]、灰关联分析法[6]、人工神经网络法[7]、Bayes判别分析法[8]等，研究对象大多为公路边坡和不涉水边坡，将这些分析方法应用到消落带岩质边坡的研究较少。蒋秀玲等[9]采用MorgensternPrice法对三峡库区水位变动下的滑坡稳定性进行了评价;刘磊磊等[10]通过AHP-理想点模型对岩质边坡进行分级评价，为岩质边坡稳定性分级评价提供了一种新的方法;司俊燕等[11]将粒子群优化算法、投影寻踪算法和逻辑斯谛曲线三者相结合，构建了岩石高边坡稳定性评价模型（PSO-PP） ，不仅提高了精确度，而且提高了运算速度;朱玉平等[6]采用灰关联分析法对岩质边坡稳定性进行评价，评价结果通过工程实例验证了其精确性;何翔等[7]将神经网络与遗传算法结合起来，建立边坡稳定性评价体系，从而使预测结果更加精准。工程实践表明，边坡稳定性的影响因素有很多，且各个因素之间并不是单一的关系[12]。岩体质量问题是一类复杂的矛盾问题，在岩质边坡评价中需要将矛盾转化，可拓学理论可将矛盾问题转化为相容问题，运用可拓学理论对围岩进行评价是一种比较理想的方法[13-14];层次分析法可以把复杂的问题简化为若干层次和因素，在各因素间进行比较和计算，从而得到各影响因素的权重，为最佳方案的选择提供可靠的依据。三峡库区消落带岩质边坡在多种荷载作用下，极易发生滑坡、崩塌等地质灾害，加上周期性水位变化，基座岩体长期处于干湿循环之中，已经开始发生软化。王文沛等[15]通过分析三峡库区危岩体目前的变形和受力状态，发现危岩体的强度和稳定性持续降低。在江水侵蚀、岩体压力、地下水、暴雨、人类活动等多种因素长期作用下，三峡库区形成了30 m消落带，并发生多次滑坡。针对上述问题，笔者综合考虑各种方法的优点，提出采用基于层次分析法（AHP）的可拓理论评价模型，对消落带岩质边坡稳定性进行分级评价，并将该方法应用于工程实践。

1 可拓学理论分析方法

可拓学[16]是将物元理论和可拓数学原理相结合，通过引入物元R=（N，C，V）（物，特征，量值），从可行性和优化的角度对研究对象进行定性定量评价，定性分析主要通过物元的可拓性确定，定量计算则依靠可拓集合论和关联函数。可拓学中的物元理论和可拓集合理论是岩体稳定性分析的基础，采用可拓理论分析的基本步骤如下[17-18]。

（1）确定经典域。给定事物的名称为N，它关于特征C的量值为V，通过有序的三元组R=（N，C，V）来描述事物的基本元，称之为经典域物元。则经典域的物元矩阵可表示为式中：Rji为经典域物元矩阵;Nj为第j个评价类别（j=1，2，…，m）;Ci为第i个评价指标（i=1，2，…，n）;Vji为第j个评价类别关于第i个评价指标的量值范围，即为经典域。

（2）确定节域。节域物元表示的是每一岩体级别各评价指标的权值范围。节域的物元矩阵表达式为

（3）确定待评同征物元体。根据同征物元体得出待评物元体，对于待评的事物，把所收集到的数据用物元Rt表示：

（4）确定关联度。某评价类别Ni关于等级t的关联函数为根据式（6）和式（7）可得待评物元的等级为t0。

2 层次分析法（AHP）

层次分析法[19]是20世纪70年代美国著名运筹学家Saaty提出的一种系统分析方法，通过将复杂问题中的各个因素分解成层级结构，使其成为有关联的有序层，利用判断矩阵来分析各个因素的重要性，并通过比较不同因素的重要性来确定每个因素在每个层次中的权重。层次分析法能较为准确地求出各个指标的权系数，其逻辑性、实用性都较好，被广泛应用于决策分析中。层次分析法用于评价消落带岩质边坡稳定性的步骤[10]如下。

（1）构建判断矩阵。根据工程地质条件，选取岩体透水系数、岩体完整系数、岩体单轴抗压强度、岩体结构特征、日最大降雨量、地下水状态、水位变化、黏聚力、内摩擦角、变形模量10个因素作为消落带岩质边坡稳定性评价指标。引入适当的判断标度，将指标间的相对重要性以数字的形式体现，指标重要性判断标度见表1。

（3）检验指标一致性。指标一致性检验的目的是为了避免专家的主观偏向性，保证权重分配的合理性。一致性检验判断标准采用指标CR表示，CR在不同范围内所对应的一致性检验判断标准见表2。

采用Matlab软件对判断矩阵S求特征值和特征向量，计算得出最大特征值λmax=10.827。对特征向量进行归一化处理，得到评价指标的权重向量为W=（0.275，0.220，0.191，0.066，0.092，0.048，0.033，0.023，0.017，0.036），利用式（11）、式（12）进行一致性检验，得到CR=0.062<0.1，表明其一致性很好（合理），因此得出的权重向量即为所求各评价指标的权重。

3 案例分析

为验证基于AHP的可拓理论模型用于消落带岩质边坡稳定性分析的合理性与有效性，以重庆巫山箭穿洞（见图1）岩质边坡为例进行分析。三峡库区箭穿洞危岩体地理位置特殊，一旦发生失稳滑坡，损失将非常大。张枝华等[20]研究发现箭穿洞危岩主要为三叠系下统大冶组第四段（T1d4），岩体较完整且强度高，主要为灰色、肉红色的中-厚层状灰岩;高程280 m以上为嘉陵江组第一段（T1j1），岩体完整，但表层风化强烈，主要为薄-中厚层的白云岩;基座以下为大冶组第三段（T1d3），岩体破碎且强度低，主要为灰白色的薄-中厚层状泥质灰岩。

3.1 参数确定

用单因素法将岩体質量分为5个等级，根据水利水电边坡工程的相关规范及国家标准[21-22]和专家打分法[18，23-25]，以及库水位变化时边坡稳定性规律，得出消落带岩质边坡稳定性评价指标分类标准（见表4）。

3.2 经典域和节域的确定

根据表5无量纲化的单因素评价标准，取Ⅰ～Ⅴ级消落带岩体质量指标对应的取值范围作为经典域（10个因素分别记为c1～c10），节域根据岩体质量等级确定。

3.3 待评物元的确定

3.4 计算箭穿洞危岩级别的关联度

3.5 箭穿洞岩质边坡稳定性级别确定

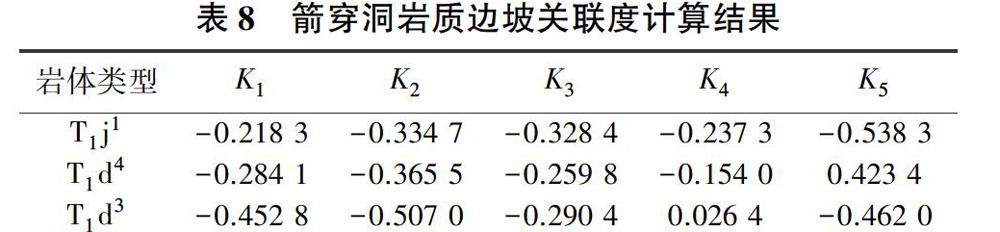
根据式（7）和表8，可以判断该岩体所处的稳定性级别。由于max Kj（T1j1）=K1，max Kj（T1d4）=K4，max Kj（T1d3）=K4，因此岩质边坡T1j1属于Ⅰ级（稳定），岩质边坡T1d4和T1d3属于Ⅳ级（欠稳定）。综合判断，箭穿洞岩质边坡处于欠稳定状态，需要对基座和危岩进行加固处理，这与张枝华等[20]对箭穿洞危岩稳定分析的结果一致，说明基于AHP-可拓理论的消落带岩质边坡稳定性分析方法可以用于实际工程中。

4 结 语

鉴于消落带岩质边坡的岩体物理力学性质和公路边坡岩体有所不同，采用层次分析法确定评价指标权重，结合可拓理论分析消落带岩质边坡稳定性，并通过具体案例验证了该方法的有效性与可行性。

（1）选取单轴抗压强度、岩体质量指标、变形模量、岩体透水系数、地下水发育程度、日最大降雨量、消落带水位变化、岩体结构面特征、黏聚力、内摩擦角10个因素为预测指标，采用层次分析法计算影响边坡稳定性的各个指标权重，运用可拓理论建立了消落带岩质边坡稳定性分级方法。

（2）运用该方法对重庆巫山箭穿洞岩质边坡进行分析，结果表明：箭穿洞岩质边坡上部较为稳定，基座和围岩中下部处于欠稳定状态，需要对其进行加固防护处理。该结论与张枝华对箭穿洞危岩的分析结果相符合，因此可以将该方法运用到三峡库区消落带岩质边坡的稳定性分级评价中。

（3）消落带岩质边坡地理位置特殊，稳定性评价和工程建设中要统筹考虑多方面因素，对存在风险的边坡要及时采取合理的治理措施。

参考文献：

[1] 唐辉明，马淑芝，刘佑荣，等.三峡工程库区巴东县赵树岭滑坡稳定性与防治对策研究[J]. 地球科学，2002，27（5）：621-625.

[2] COJEAN R，CAI Y J.Analysis and Modeling of Slope Stability in the ThreeGorges Dam Reservoir （China）：the Case of Huangtupo Landslide[J].Journal of Mountain Science，2011，8（2）：166-175.

[3] 李智慧，贾苍琴，王贵和，等. 水位骤降对边坡稳定性影响研究综述[J].水利水电科技进展，2011，31（增刊1）：86-90.

[4] 叶海旺，常剑. 基于模糊决策和层次分析法的采矿方法选择[J]. 武汉理工大学学报，2009，31（8）：145-148，153.

[5] LI L，LI Y M. The Designand Stability Analysis of Adaptive System Based on Linear T-S Fuzzy System[J]. Acta Automatica Sinica，2003，29（6）：1024-1026.

[6] 朱玉平，莫海鸿. 灰关联分析法在岩质邊坡稳定性评价中的应用[J].岩石力学与工程学报，2004，23（6）：915-919.

[7] 何翔，李守巨，刘迎曦，等. 岩土边坡稳定性预报的人工神经网络方法[J]. 岩土力学，2003，24（增刊2）：73-76.

[8] 文畅平. 岩体质量分级的Bayes 判别分析方法[J]. 煤炭学报，2008， 32（4）：395-399.

[9] 蒋秀玲，张常亮.三峡水库水位变动下的库岸滑坡稳定性评价[J]. 水文地质工程地质，2010，37（6）：38-42.

[10] 刘磊磊，张绍和，刘利茂.岩质边坡稳定性分级的 AHP-理想点模型及应用[J].中南大学学报（自然科学版），2014，45（10）：3499-3504.

[11] 司俊燕，郭海庆，徐飞，等. PSO-PP模型在岩石高边坡稳定性评价中的应用[J]. 水电能源科学，2011，29（1）：79-82.

[12] 高玮.基于蚁群聚类算法的岩石边坡稳定性分析[J]. 岩土力学，2009，30（11）：3476-3480.

[13] 姚令侃. 可拓学在泥石流预报减灾决策上的应用[J]. 系统工程理论与实践，1998，18（1）：139-144.

[14] 贾超，肖树芳，刘宁. 可拓学理论在洞室岩体质量评价中的应用[J]. 岩石力学与工程学报，2003，22（5）：751-756.

[15] 王文沛，李滨，黄波林，等.三峡库区近水平厚层斜坡滑动稳定性研究：以重庆巫山箭穿洞危岩为例[J]. 地质力学学报，2016，22（3）：725-731.

[16] 蔡文.物元模型及其应用[M].北京：科学技术出版社，1994：21-25.

[17] 黄祥志，佘成学.基于可拓理论的围岩稳定分类方法的研究[J]. 岩土力学，2006，27（10）：1800-1804.

[18] 康志强，冯夏庭，周辉. 基于层次分析法的可拓学理论在地下洞室岩体质量评价中的应用[J]. 岩石力学与工程学报，2006，25（增刊2）：3688-3690.

[19] DUBOIS D， PRADE H. Fuzzy Sets and Systems， Theory and Applications[M]. New York：Academic Press，1998：25-39.

[20] 张枝华，杜春兰，余姝. 三峡库区巫峡箭穿洞危岩体稳定性分析及防治工程设计[J].中国地质灾害与防治学报，2018，29（2）：48-54.

[21] 中华人民共和国水利部.工程岩体分级标准： GB 50218—94 [S].北京：中国计划出版社，1995：4-10.

[22] 中华人民共和国水利部.水利水电工程地质勘察规范： GB 50287—99 [S].北京：中国计划出版社，1999：52-68.

[23] 王新民，康虔，秦健春，等. 层次分析法-可拓学模型在岩质边坡稳定性安全评价中的应用[J].中南大学学报（自然科学版），2013，44（6）：2456-2461.

[24] 刘华伟. 基于可变权重理想点法的边坡稳定性评价[J]. 水电能源科学，2014，32（5）：101-104.

[25] 任洋，李天斌，熊国斌，等. 基于可拓理论的高地应力隧道围岩分级及应用[J]. 工程地质学报，2012，20（1）：66-73.

[26] 吴贤国，王洪涛，何云. 基于模糊物元的岩溶隧道开挖稳定性评价[J]. 中国安全科学学报，2018，28（1）：99-104.

[27] 朱维伟. 基于可拓学的公路边坡稳定性评价与防治策略研究[D].南京：南京林业大学，2013：44-46.

[28] 仉文岗，王尉，高学成. 库区水位下降对库岸边坡稳定性的影响[J]. 武汉大学学报（自然科学版），2019，52（1）：21-25.

【责任编辑 张华兴】