基于D-S证据理论的子午河流域洪水预报模型优选

肖瑜 刘茵 苏岩

摘 要：洪水预报作为重要的防洪非工程措施，是减少洪水损失不可或缺的手段。以洪水预报模型优选为目标，根据三河口水利枢纽所在流域子午河流域的降雨径流规律和产汇流特性，以及三河口水利枢纽的施工导流方案和度汛标准，选择流域2010—2015年实测13场历史雨洪資料，采用新安江模型（简称XAJ模型）、API模型、TOPMODEL模型模拟历史洪水过程，以洪峰流量、峰现时间、合格率、确定性系数4个指标为模型综合优选指标体系，引入D-S证据理论选择流域洪水预报适宜模型。结果表明：3个模型洪水模拟结果可信度分别为0.824（XAJ模型）、0.813（API模型）、0.883（TOPMODEL模型），TOPMODEL模型在流域洪水模拟综合测评中表现相对最优，可应用于三河口水利枢纽施工期洪水预报。

关键词：洪水预报;多模型;D-S证据理论;三河口水利枢纽

中图分类号：TV121 文献标志码：A

doi：10.3969/j.issn.1000-1379.2020.12.009

Abstract： As an important nonengineering measure of flood control， flood forecasting is an indispensable means of decreasing floodwater disaster. According to the law of rainfall runoff and the characteristics of runoff generation and convergence of Ziwu River basin where Sanhekou HydroJunction is located， as well as the construction diversion scheme and the standard of flood retaining and control of Sanhekou HydroJunction Project， the paper aimed at selecting the optimum flood forecasting model， 13 historical flood data measured in the basin from 2010 to 2015 were chosen and three models which were Xinanjiang Model（XAJ Model for short）， API Model and TOPMODEL Model were used to simulate historical flood process. Furthermore， four indexes of flood peak discharge， occurrence time， qualification rate and certainty coefficient were taken as the index system of model optimization and DS evidence theory was introduced to select a suitable model for river basin flood forecasting. The result indicates that the reliability of XAJ Model is 0.824， API Model is 0.813 and TOPMODEL Model is 0.883， so TOPMODEL Model is relatively optimal in the comprehensive evaluation of basin flood simulation， which can be applied to the flood forecasting of Sanhekou HydroJunction Project during the construction period.

Key words： flood forecasting; multimodels; DS evidence theory; Sanhekou HydroJunction Project

我国是一个洪涝灾害频繁发生的国家[1]。洪水预报是防灾减灾的重要非工程措施，经过多年的预报理论发展和实践，我国的洪水预报技术有了长足的发展，特别是近年来分布式水文模型的迅速发展[2]，使得河流的洪水预报更简单快速，甚至几分钟就可以得到多种模型的预报结果，但这也带来了哪种预报方案最优这一新的问题，这其实是多属性决策问题。

多属性决策本质就是在多个属性信任度之间的权衡[3]，在各行各业、各个领域都有应用，比如水质评价[4]、体系评估[5]、风险评价[6]、工程投资决策[7]、方案优选[8]等。朱志强等[4]采用G2赋权法确定主观权重，采用CRITIC赋权法确定客观权重，并考虑到组合赋权的可信性，引入Kullback相对熵理论，运用正态云模型对水质状况进行识别和比较分析，充分反映了水质的变化趋势;佟瑞鹏等[5]提出评估安全管理体系的2个层级指标，构建结构方程模型（SEM）用于分析各评价指标的关系，并根据模型变量间的效应系数计算各级指标的权重系数，并通过实例应用验证了该评价指标的适用性和有效性;彭康等[6]根据尾矿库溃坝的特点和成因，选择防洪设计标准等16项未确知测度函数评价指标，建立尾矿库溃坝风险分级预测的未确知测度评价模型，丰富了尾矿库溃坝危险性的评价方法;杨开云等[7]以模糊数学和灰色系统的基本理论为基础，提出多目标灰色关联度法的概念，建立了多目标灰色关联度决策模型，并应用到实际投资决策中;郑伯坤等[8]基于未确知测度理论，选择对充填系统影响较大的12个因素作为评价指标，建立了充填工艺方案评价模型并应用于三山岛金矿充填工艺的方案优选;王文川等[9]针对水利工程方案优选过程中主观赋权的随意性和不确定性，通过博弈论思想将序关系分析法（G1）确定的主观权重和熵值法确定的客观权重进行组合优化，结合灰色关联理论构建了博弈论组合赋权的灰色关联模型;刘锋等[10]在综合考虑从优隶属度和灰色关联的基础上，提出改进灰色关联模糊决策方法，建立技术指标权重集和灰色关联系数矩阵，通过综合评价模型，实现了设计方案的模糊优选，有效减少了评价过程中的主观因素干扰。综上所述，多属性决策分析其实是确定和不确定之间的一场博弈，而D-S证据理论能够很好地表示“不确定”[11]，目前已经被广泛应用于处理多属性决策问题分析，因此本文尝试采用证据理论来解决多模型洪水预报方案的优选问题。

本研究以三河口水利枢纽所在流域为例，采用D-S证据理论对三河口水利枢纽施工期洪水预报方案进行优选。首先采用3个不同的洪水预报模型（XAJ模型、API模型、TOPMODEL模型）对三河口水利枢纽施工期进行洪水预报;然后对洪峰流量、峰现时间、合格率、确定性系数4个指标进行无量纲化和归一化处理，建立了基于多模型洪水预报的基本信任分配函数;最后按照D-S证据合成规则分别计算出3个模型对应的可信度，并得出TOPMODEL模型对应的洪水预报方案为最优预报方案的结论，丰富了洪水预报方案优选的方法。

1 基于D-S证据理论的洪水预报模型优选体系的建立

D-S证据理论是一种先验知识的不确定性推理方法[12]，起源于20世纪60年代哈佛大学数学家A.P. Dempster利用上、下限概率解决多值映射问题，1967年起A.P. Dempster连续发表一系列论文，标志着证据理论的正式诞生[13]。后来Dempster的学生G.Shafer进一步发展了证据理论，并引入信任函数概念，形成了一套“证据”和“组合”来处理不确定性推理的数学方法，并在1976年出版了《证据的数学理论》，标志着证据理论已经发展为一种处理不确定性问题的完整理论[14]。D-S证据理论不需要知道先验概率，能够很好地表示“不确定”，被广泛用来处理不确定数据，主要适用于情报分析、信息融合、法律案件分析、专家系统、多属性决策分析等方面。

在D-S证据理论的应用过程中，基本概率赋值函数（简称BPA）的生成是关键且核心的步骤[15]，对本研究而言，就是如何利用多模型洪水预报的成果构建洪水预报的BPA。洪水预报模型优选的依据是《水文情报预报规范》（GB/T 22482—2008），洪水预报精度评定的项目包括水位、流量（洪峰）、洪水过程等预报要素，评定指标目前主要是合格率;洪水预报误差的指标包括相对误差、绝对误差、确定性系数。因此，本研究的关键就是选择能够表示洪水特征和预报精度的指标，对指标进行无量纲化和归一化处理，从而生成BPA，然后利用D-S证据理论合成规则计算3个模型的可信度。

2 三河口水利枢纽洪水预报模型优选

2.1 工程概况

三河口水库是引汉济渭调水项目的主干工程之一，坝址位于汉中市佛坪县大河坝镇，椒溪河、蒲河、汶水河汇合口（即三河口）下游2 km处，控制流域面积2 186 km2，占全流域的72.6%，坝址处河床高程525 m（黄海）。

三河口水库所在区域的椒溪河、蒲河、汶水河、黑河等及其支流地处中高山区，暴雨多发频发，河床纵比降较大，坡面汇流速度快、时间短，河道洪水涨落急剧。历史上，该区域河流曾多次发生大洪水和特大洪水，如“02·6·9”特大暴雨洪水，椒溪河佛坪县城河段、蒲河陈家坝河段的洪峰流量分别高达1 900、2 400 m3/s，椒溪河、蒲河、汶水河河口段的洪峰流量分别达1 430、2 800、3 500 m3/s。三河口水利枢纽及秦岭隧洞部分支洞施工地点，位于主河道或河岸附近，施工区与生活区多依山傍河，地形复杂，人员及施工设备极易受暴雨洪水的威胁，为确保工程施工期安全，必须选择适宜的洪水预报模型，制定洪水预报方案，为科学安排施工和组织预防、抢险、撤离争取时间。

2.2 多模型洪水预报

XAJ模型、API模型、TOPMODEL模型在陕西省部分流域洪水预报中广泛应用。XAJ模型适用性很强，这几年经过不断改进和发展，在洪水预报方面取得了较好的应用效果，在陕南地区和关中部分区域应用也较多，它用一种比较简单的函数关系表示径流形成过程的空间变化特性，是一种概念性模型。李文泰[17]建立丹巴水文站新安江模型，并经过对比分析证明了该模型的有效性和可用性;郭君[18]以清江流域为研究对象，设置了三层水箱模型，提高了预报精度，证明了XAJ模型的适用性。API模型在资料条件较好的中小河流应用比较广泛，属于多输入单输出静态的概念性模型。谢静[19]采用API模型对典型暴雨区荥经河进行洪水预报演算，取得了良好效果。TOPMODEL模型結构简单、参数少、物理概念明确、实用性较强，属于半分布式流域水文模型。苏万敏[20]以半湿润半干旱山丘区的冰峪沟小流域为研究对象，采用新安江模型和TOPMODEL模型进行该流域7场历史洪水的模拟研究，并得出2个模型在该流域具有较好的适用性。

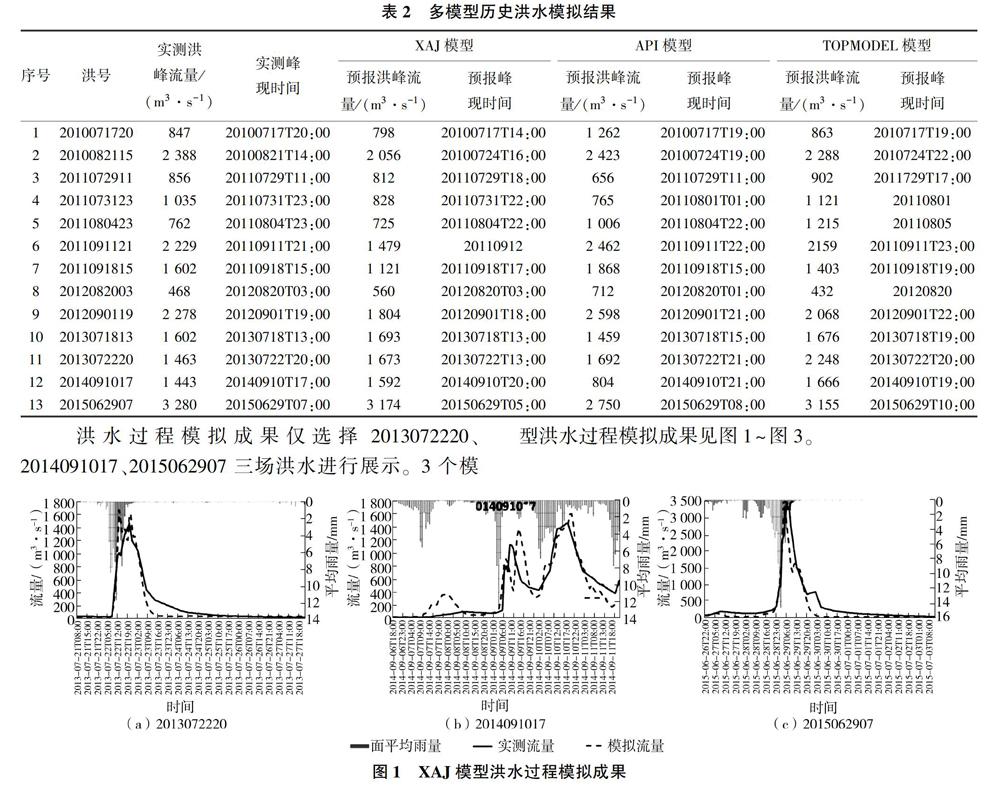
本研究针对三河口水库区域水文特性和下垫面特点，考虑水文资料、地形地貌、土地利用等资料情况，以及模型实用性，选择大河坝水文站2010—2015年实测13场雨洪资料，分别采用XAJ模型、API模型、TOPMODEL模型模拟历史洪水过程，洪峰流量和峰现时间模拟结果见表2。

2.3 方案优选

步骤1，根据上述D-S证据理论与多模型洪水预报的耦合方式，选择洪峰流量、峰现时间、合格率、确定性系数共4个能够体现洪水特征和预报精度的指标作为“证据”，通过式（8）～式（11）得到D-S证据理论的BPA，见表3。图2 API模型洪水过程模拟成果

3 结 语

采用XAJ模型、API模型、TOPMODEL模型分别模拟了大河坝水文站2010—2015年共13场历史洪水过程，并选择洪峰流量、峰现时间、合格率、确定性系数4个能够体现洪水特征和预报精度的指标作为“证据”，生成D-S证据理论的BPA，最后依据证据合成规则计算3个模型洪水模拟结果的可信度，结论如下：

（1）3个模型对历史洪水的模拟基本都是满足洪水预报许可误差的;

（2）洪峰流量、峰现时间、合格率、确定性系数4个指标作为“证据”是合理的;

（3）3个模型的可信度分别为0.824（XAJ模型）、0.813（API模型）、0.883（TOPMODEL模型），TOPMODEL模型在流域洪水模拟综合测评中表现相对最优，可应用于三河口水利枢纽施工期洪水预报;

（4）本研究对D-S证据理论的应用丰富了洪水预报方案优选的方法，为决策者提供了更为客观、科学的决策支持。

参考文献：

[1] 张杰平.跨流域调水补偿制度创新研究[D].武汉：武汉大学，2012：15-16.

[2] 张红萍.山区小流域洪水风险评估与预警技术研究[D].北京：中国水利水电科学研究院，2012：10.

[3] DAVID L O. Simulation of Fuzzy Multiattribute Models for Grey Relationships[J]. European Journal of Operational Research， 2005， 175（1）：111-120.

[4] 朱志强，唐金平，张强，等.基于博弈论组合赋权的正态云模型在地下水水质评价中的应用[J].节水灌溉，2019（6）：43-46.

[5] 佟瑞鹏，张浩.基于结构方程模型的安全管理体系评估与实证分析[J].中国安全生产科学技术，2017，13（5）：157-162.

[6] 彭康，李夕兵，王世鸣，等.基于未确知测度模型的尾矿库溃坝风险评价[J].中南大学学报（自然科学版），2012，43（4）：1447-1452.

[7] 杨开云，朱峰，赵刚.基于多目标灰色关联度的工程投资方案优选[J].人民黄河，2009，31（2）：72-73.

[8] 郑伯坤，尹旭岩，黄腾龙，等.基于未确知测度理论的三山岛金矿充填工艺方案优选[J].矿业研究与开发，2020，40（2）：13-18.

[9] 王文川，马俊清，徐冬梅，等.基于博弈论的灰色关联模型在水利工程方案优选中的应用[J].水利规划与设计，2020（1）：55-58.

[10] 刘锋，魏光辉.基于灰色关联的水利工程方案模糊优选[J].水力发电学报，2012，31（1）：10-14，26.

[11] 廉伟健.基于D-S证据理论和SVM的多传感器信息融合算法研究[D].长春：吉林大学，2019：7-8.

[12] 李弼程，王波，魏俊，等.一种有效的证据理论合成公式[J].数据采集与处理，2002（1）：33-36.

[13] 冯义.发电企业成本管理与竞价优化理论与应用研究[D].北京：华北电力大学，2008：6-9.

[14] SHAFER G. A Mathematical Theory of Evidence[M]. Princeton： Princeton University Press，1976：27-30.

[15] 黃杰.基于改进D-S证据理论的网络证据融合方法研究[D].济南：山东师范大学，2019：6.

[16] 肖洁，罗军刚，张晓.基于D-S证据理论的多模型洪水预报方案优选[J].西北农林科技大学学报（自然科学版），2013，41（9）：193-199.

[17] 李文泰.基于新安江模型的丹巴水文站预报方案编制[J].四川水利，2019，40（2）：91-92.

[18] 郭君.清江流域降雨径流预报模型的研究[D].武汉：华中科技大学，2004：8-9.

[19] 谢静.API模型在中小河流预报方案编制中的应用[J].陕西水利，2018（5）：12-14.

[20] 苏万敏.小流域洪水预报方法研究及应用[D].大连：大连理工大学，2016：11-13.

[21] 曹晓军，彭会萍.基于证据可信度的D-S证据理论合成规则[J].微计算机信息，2012，28（7）：93-94.

【责任编辑 张华岩】