既有建筑幕墙平整度拟合方法的研究
2020-12-30刘永成徐迎春张泽雨姚远宏
刘永成,徐迎春,张泽雨,姚远宏
(中国建筑科学研究院天津分院,天津 300384)
0 引言
城市化进程的加快使大型建筑不断涌现,幕墙的市场需求量不断增加,一方面是幕墙建筑数量的增加,但是另一方面是其安全性能的降低,包括深圳平安金融中心、成都“环球中心”天堂洲际大饭店、人民中路国际购物中心商业街、九江市南湖国际小区等等这些幕墙建筑都相继发生了安全事故,所以幕墙检测就显得尤为重要。对于检测工作,全站仪 NP 模式以及三维激光扫描仪问世为快速获取幕墙坐标提供了有效的手段,但后期不同数据处理方法所得成果有所差异,传统最小二乘方法系数矩阵存在误差,也有人对幕墙进行小面积分区计算(无法反应幕墙整体情况具有局限性)。针对上述问题,本文提出对幕墙个点坐标与平均坐标组成的向量与法向量的数量积最小原理,运用 SVD 奇异值分解的方法,使用 MATLAB 编程求解出平面方程,最后通过算例验证了方法的可行性,为检测鉴定工作提供帮助。
1 检测与拟合推导
运用全站仪 NP 模式采集幕墙板的三维坐标[1],由于建造施工误差、建筑物变形、观测误差等影响,这些点位并不会处于同一个平面内,需要建立模型,拟合出最佳幕墙平面,计算出平整度,以检查建筑物质量是否合格。
1.1 数据采集
在进行公共商场等场所房屋安全鉴定时,需要对外侧幕墙进行平整度检测,根据现场的实际情况布设控制网,如果现场条件允许建议布设成闭合导线网,建立独立的坐标系统,并采用严密平差的方法得到各控制点坐标,最后进行碎部测量,采集幕墙板坐标[2]。
根据幕墙板大小选择合适的位置进行坐标采集,幕墙板测点位置如图 1 所示。
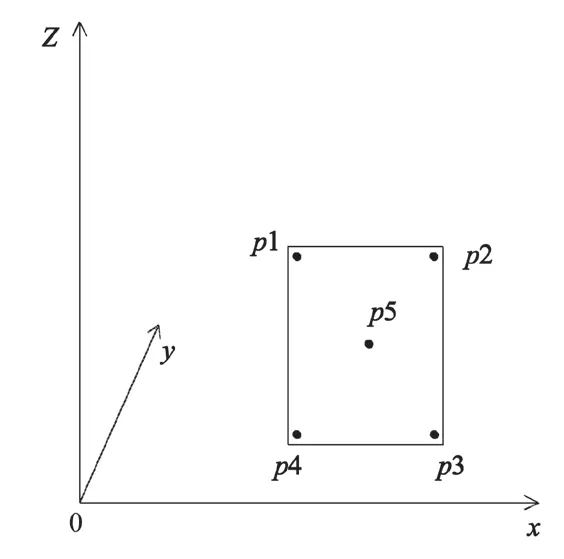
图1 幕墙板检测点位图
1.2 幕墙拟合方法推导
假设采集同一平面坐标点为(xi,yi,zi),拟合出的平面方程如式(1)所示,约束条件如式(2)所示。

式中:x,y,z 为坐标值,A、B、C 为平面方程系数,D 为常数。

式中:A、B、C 为平面方程系数,m 为常数。
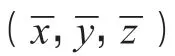

式(1)-式(3)得出式(4)
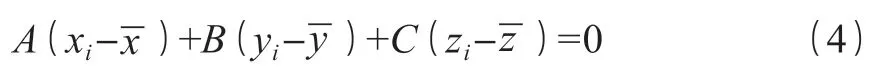
可以写成:

如果式(5)成立需要所有点都在平面上,实际情况由于施工误差、幕墙自身变形以及观测误差导致一定有部分点在平面之外,这就需要进行拟合使所有点与平面的距离之和最小,故使:

式中:β,X 为式(5)矩阵。
约束条件为

式中:X 为式(5)矩阵,m 为常数。
对 β 进行奇异值分解:

式中:β 同式(5),D 是对角阵,U 和 VT均为正交矩阵(酉矩阵)。
根据正交不变性,则:
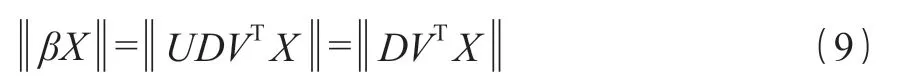
式中符号同式(5)、式(8)。
其中 VTX 为列矩阵,根据酉矩阵的性质可得:

式中符号同式(7)、式(8)。
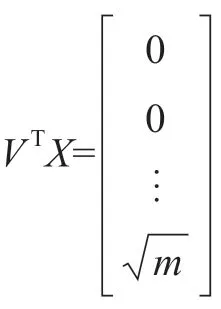
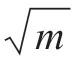
每个观测点 pi到拟合平面的距离,如式(11)所示。

式中:di为观测点到拟合平面的距离,其他符号同式(4)。
幕墙平面的平整度如式(12)所示。

式中:M 为平整度,n 为拟合所需坐标点数,其他符号同式(11)。
2 工程实例
以天津市塘沽区金街大型商场为例,天津中原百货滨海有限公司经营场所为一栋地上 4 层的商业建筑,坐落于天津市滨海新区上海道 629 号。据可查资料,该建筑设计于 2001 年,设计名称为“天津市塘沽区新百商贸股份有限公司”,结构形式为钢框架结构,建筑外墙采用加气混凝土砌块填充墙,部分墙体外做彩色压型钢板墙面,靠近金街一侧墙体外做封闭式铝塑板幕墙,两种围护结构做法均未见有效设计资料。
2.1 确定控制点
根据现场情况布设 5 个控制点(见图 2),并运用全站仪以及水准仪进行控制网测量,后期内业工作时运用 Cosawin 平差软件进行数据处理,所得坐标如表 1 所示。布点时注意一测站能扫到整面幕墙板,否则增加的测站误差影响数据成果。
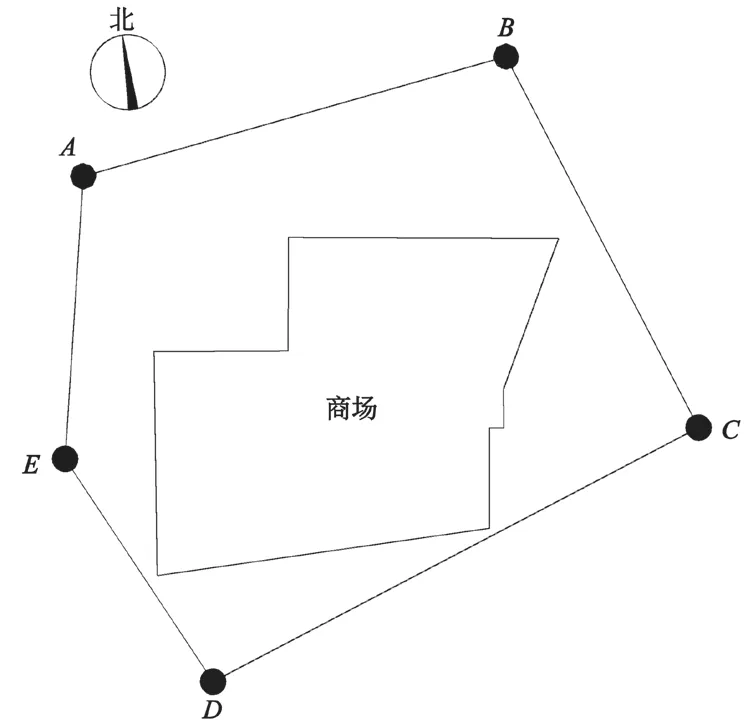
图2 控制点布置示意图
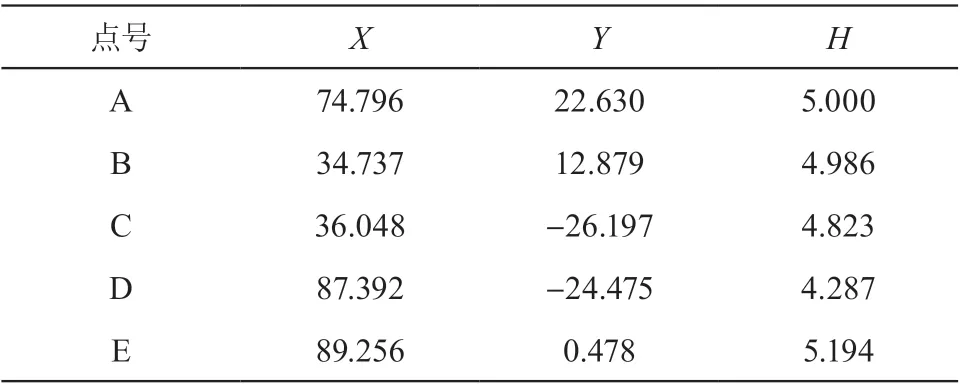
表1 控制点平差成果表 m
2.2 数据采集
用全站仪免棱镜模式根据图 1 进行幕墙目标点采集工作,本项目共采集 1 053 个坐标点,记录时不仅要记录点号,还要提前画好立面图并编辑好轴号(见图 3),后期对数据分析时便于找出变形过大的幕墙板进行针对性查勘。由于篇幅有限本文仅对东区北侧幕墙数据进行分析。
2.3 计算方法
根据 SVD 奇异值分解进行 MATLAB 软件编程进行处理,以下为主要编程思路。
xyzdata=[坐标];
xyzping=mean(xyzdata,1);% 求坐标平均值
β=bsxfun(@minus,xyzdata,xyzping);% 根据式(4)建立系数矩阵
[U,S,V]=svd(β);% 奇异值分解
a=V(1,3);
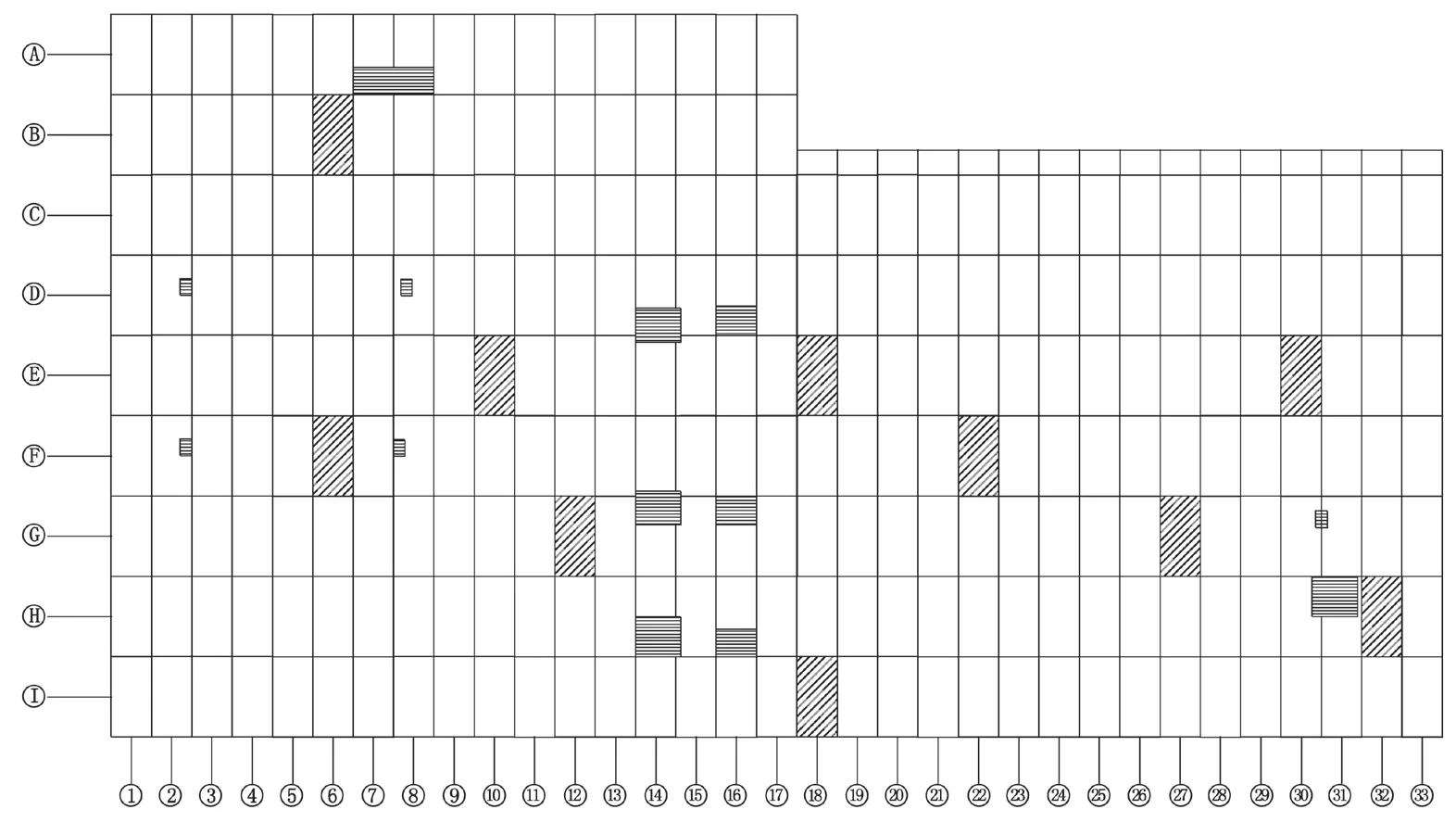
图3 东区幕墙板立面图
b=V(2,3);
c=V(3,3);
d=-dot([a b c],xyzping);
di=abs(x*a+y*b+z*c+d)/sqrt(a2+b2+c2);
经过对东区北侧幕墙板的计算求出右奇异矩阵:

所以拟合平面方程为a x+b y+c z+d=0(a= -0.517 953 403 239 086;b=-0.855 405 555 215 044; c=-0.002 368 159 684 488 78;d=12.088 835 417 622 9);并计算出每个坐标点到拟合平面的距离 di与平整度如表 2 所示。
根据坐标以及测点到拟合平面距离运用 MATLAB 进行绘图,得到平整度图(见图 4),图 4 过渡颜色比较明显,说明平整度比较差;后期根据数据计算情况找到数值过大点位,找到超限值的幕墙板,见表 2 中 18-D 轴幕墙板点位到拟合平面距离为 26 mm,通过拆除查勘发现幕墙板龙骨锈蚀严重等问题(见图 5),为鉴定提供帮助。
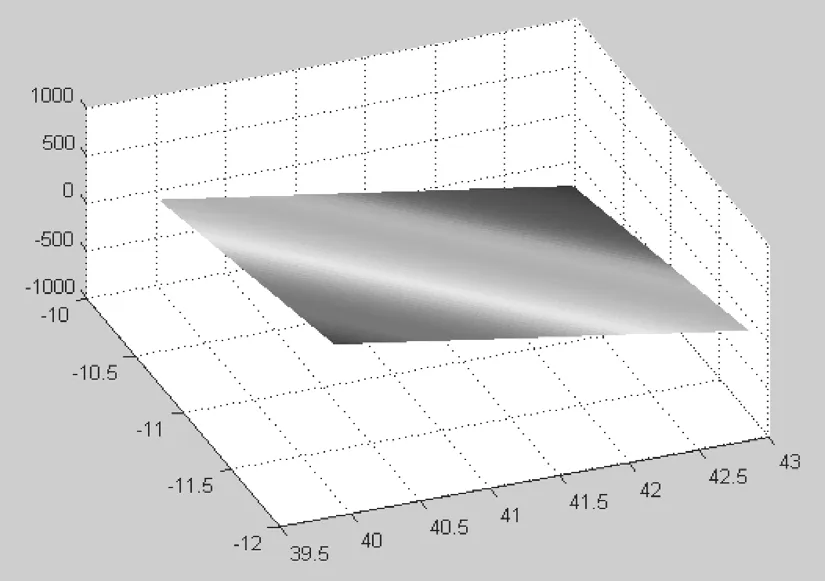
图4 东区北侧幕墙平整度图

图5 东区北侧幕墙横梁锈蚀
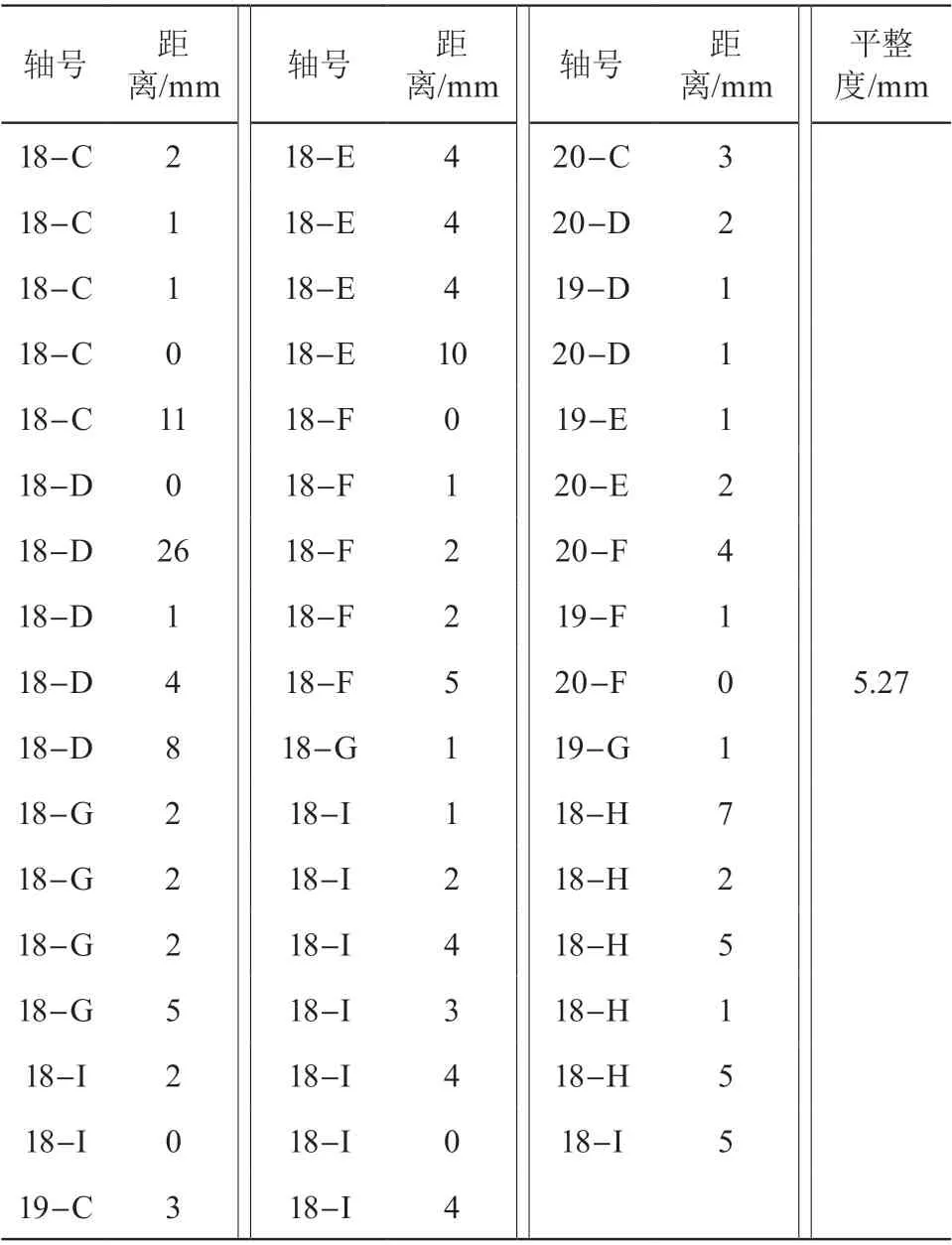
表2 坐标点到拟合平面距离与平整度(SVD)
2.4 成果与 spss 软件对比
运用 spss 软件解多元线性回归,首先建立多元线性回归方程模型 Z=β1X+β2Y+β3,把东区北侧 50 个幕墙坐标点导入到 spss 软件中,在分析中选择线性回归,置信区间级别选择 95 %、R 方变化量、模型拟合。软件运算结果模型吻合程度如表 3 所示、方程系数如表 4 所示,根据方程系数计算出每个坐标点到拟合平面的距离如表 5 所示。
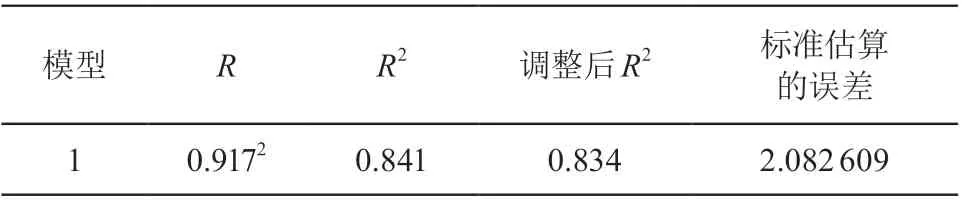
表3 模型摘要

表4 系数 a
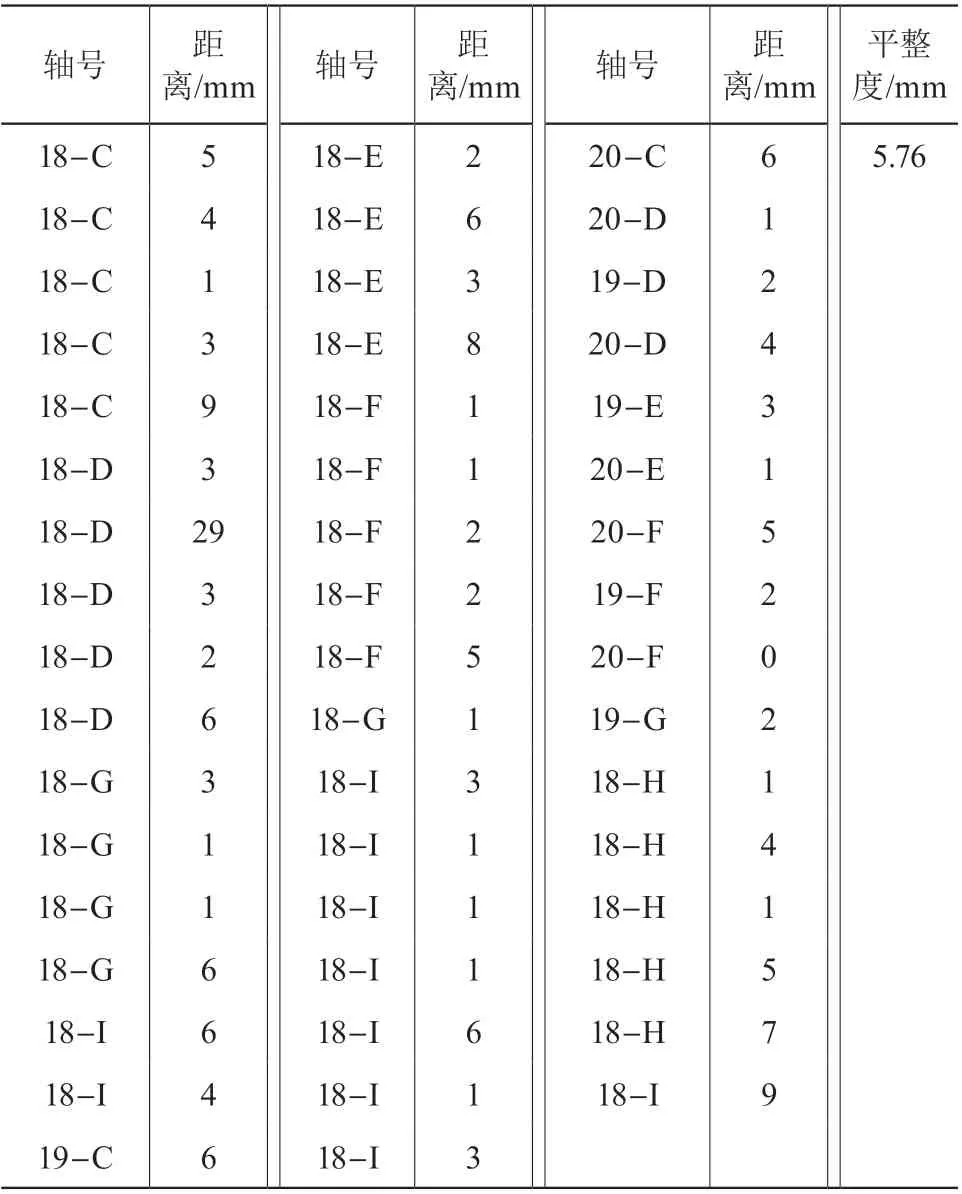
表5 坐标点到拟合平面距离与平整度(spss)
可以看出置信区间在 95 %,回归方程为 Z=-183.236 X-302.833 Y+4 275.919。
带入坐标点求得平整度为 5.76 mm,通过表 2 与表 5 对比分析,SVD 算法中点位到拟合平面距离之和小于 spss 中运算的结果,说明 SVD 方法拟合成果较好。
3 结论
幕墙建筑在施工和使用过程中的安全问题日益突出,幕墙检测鉴定显得尤为重要,本文对幕墙平整度检测以及数据处理提出了有效可靠的方法。
1)文章对幕墙平整度检测的外业观测方法以及内业数据处理(采用法向量与各平面向量数量积最小原则,运用 SVD 奇异值分解求拟合平面方程)做出了系统的说明,SVD 解法与传统数据拟合方法对比结果更为准确、合理。
2)SVD 数据处理方法对于幕墙平整度检测具有重要意义,并通过工程实例验证所得数据与现场实际情况相符,为工程实践提供了一定的参考价值,但是此方法对粗差剔除方面还需进一步研究。
