基于客流需求的城市轨道交通行车计划与列车时刻表优化

曹璐，曹成铉

(北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044)

维系一座城市正常运转必不可缺的是城市内的公共交通，相比于其他公共运输方式，轨道交通优势明显。如何提高城市轨道交通的运输效率，是近些年研究的重点之一，行车计划和列车时刻表的优化中起到了关键作用。行车计划决定了各个时间段的列车开行数量和运用车辆，是城市轨道交通一系列工作的基础。列车时刻表决定了列车在每个站的到发时间以及是否停车等，是城市轨道交通运营组织的重要内容。

针对行车计划，以往主要研究行车间隔和列车开行对数。王树文[1]根据掌握的客流时空分布特性，利用有序样品最优分割法分割运营时段，提出行车间隔和开行对数优化模型。孙焰等[2]以实载率最大化和时间分段数最小化为目标研究多个循环区段上的列车开行对数，分步优化确定行车计划。洪玲等[3]分析客流分布特征、列车交路形式和服务水平与行车间隔之间的相互影响关系，给出了行车间隔与实际客流需求和系统能力的变化趋势线。

国内外学者也对列车时刻表进行了一系列的研究。Zhang等[4]以乘客总出行时间最小化为目标建立两种非线性非凸规划模型，对时刻表进行优化使其适应拥挤条件下的动态客流需求。Niu等[5]以乘客的总等待时间最小化为目标建立非线性规划模型，并引入二元整数规划模型表示乘客的到站和离开，实现了过饱和情况下列车时刻表优化。张璐[6]提出乘客出行能量消耗反映列车的拥挤情况和乘客的等待时间，并以乘客等待时间最小和出行能量消耗最小为目标建立了两个模型。Hassannayebi等[7]以乘客的平均出行成本最小为目标，创建优化模型，使用拉格朗日松弛算法将模型简化，有效缩短了模型计算的时间。王一阁[8]从乘客出行费用出发，利用遗传算法，在预测客流的基础上优化时刻表中列车的发车间隔和停站时间, 降低了车载乘客数与车载定员之差，减少了乘客的候车时间和乘车时间。Sun等[9]计算了总出行等待时间和列车能源消耗，求得使乘客和运营商两者利益达到平衡的列车时刻表。

遗传和声算法(genetic harmony algorithm)是将遗传算法与和声算法结合的改进启发式算法，目前已经被应用到很多复杂问题的优化中。韩红燕等[10]为了验证改进遗传和声算法的可行性对6个测试函数进行仿真，结果显示改进后的算法计算结果更优，而且能提高搜索效率，更容易跳出局部极小。王英博等[11]设计了车辆配送路径优化模型，在求解时使用了改进的遗传和声算法，减轻了初始记忆库对算法的影响，使求解时间减少，并提高了准确性。张风荣[12]提出遗传和声算法能够帮助提高解的质量，提升算法跳出局部极小的能力。

综上所述，目前的研究倾向于单独讨论行车计划或单独优化列车时刻表。在此基础上，本文将行车计划的结果作为列车时刻表优化的约束条件，将两者结合从而获得更好的优化效果。在模型求解时，设计遗传和声算法求解，并通过计算比较，验证了该算法对于解决本文提出的优化模型的合理性和准确性。

1 行车计划和列车时刻表优化

在一条单线循环的线路中，如图1所示，共有2K个车站。车站的编号依次为1,2,…,K，车站1和K分别表示每条线路的起点和终点，列车在线路上循环行驶。为了使模型的表述更加简单，将图1所示的循环线路分成两个方向：f=1表示上行方向；f=2表示下行方向。由于两条线路方向相反，认为乘客不换乘即乘客的需求相互独立。

图1 轨道交通单线循环示意图

1.1 模型假设和参数规定

为了使模型的表达更加清晰，本文主要作了以下假设：

注：T为计划期结束时刻。

(2)折返站有足够的容量容纳来的列车。除了折返站，一个车站每次只能接受一辆列车，网络上不会发生越行。

(3)如果折返站的列车超过一辆，在调度时遵循先来先服务原则。

(4)列车循环受最小车头时距和折返站的折返时间的限制。

(5)在折返站对向到达的车辆优先折返发车，在对向车辆没有到达时，采用备用车辆，没有备用车辆不发车。

(6)列车在运行中采取站站停的停站方式。

本文的优化分两步进行，首先给出行车计划，然后以此为基础优化列车时刻表，模型参数如表1所示，变量如表2所示。

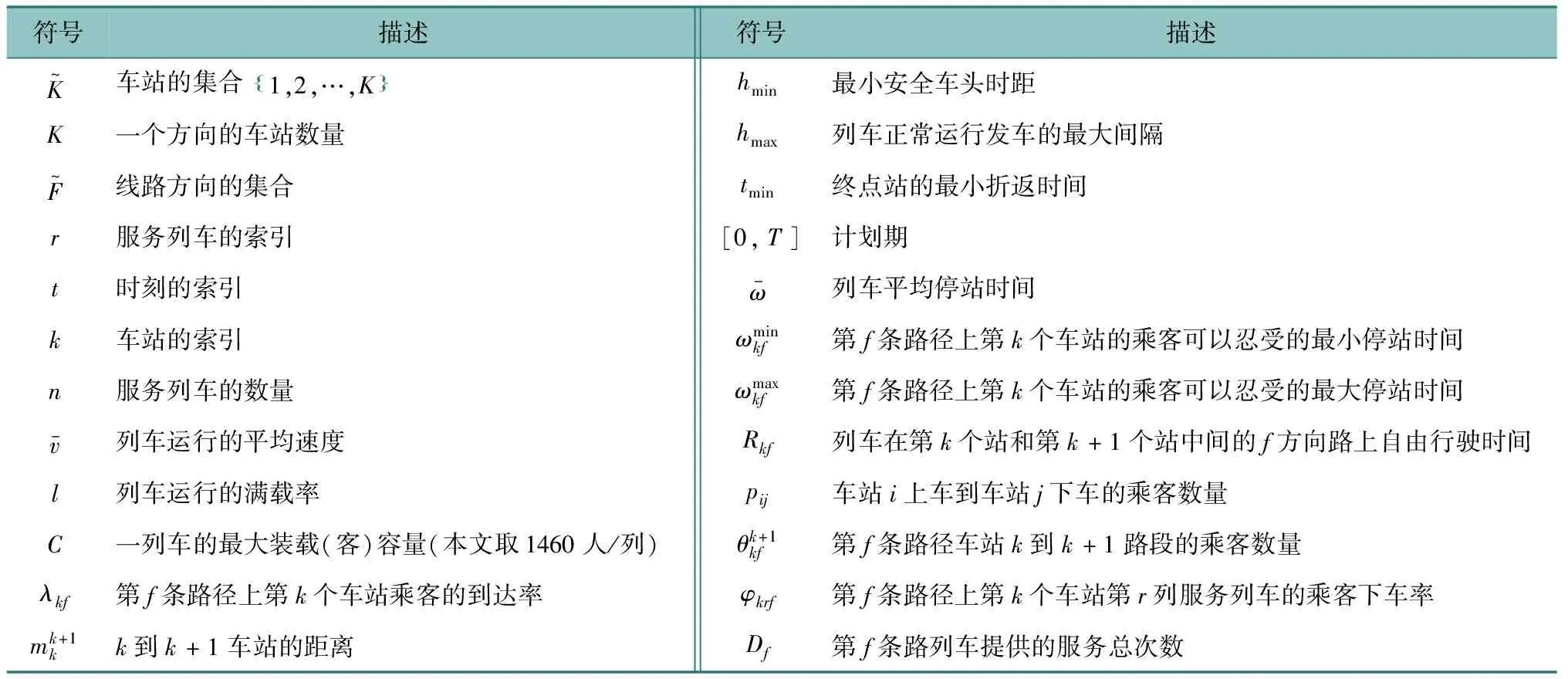
表1 模型参数

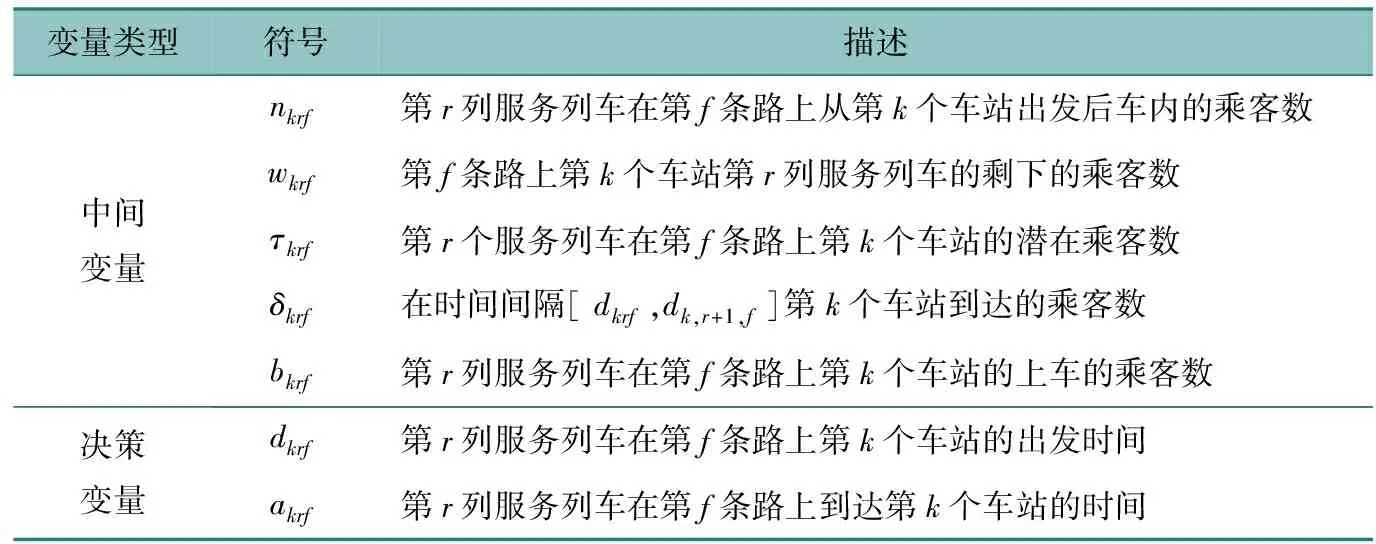
表2 中间变量与决策变量

1.2 行车计划

为了满足线路上的客流需求，同时节约城市轨道系统运能和运输资源，在规定了研究计划期后，结合最大断面客流、列车容量、设计满载率和最大发车间隔等影响因素。不考虑列车跳停，计划期开行的列车数按照如下公式计算：

(1)

为了保证公式(1)计算的开行对数有意义，要求地铁公司在车辆段必须准备一定数量的运用列车数，该列车数与高峰小时列车开行对数、每列车的编组数以及列车周转时间有关。本文假设每辆列车为6辆车编组，需要的列车数nf按如下公式计算：

(2)

通过计算得出能够满足乘客需求的行车计划。

1.3 列车运行时刻表优化

为了更好地描述模型，对文中的中间变量进行简单计算，第k个车站对于第r个列车的潜在乘客数按照公式(3)、(4)进行计算，是第r-1列车离开后第k个车站剩下的乘客与第k个车站在时间间隔[dk,r-1,f，dkrf]新到达的乘客数量之和，而对第一辆列车来说是列车到达车站之前到达的乘客数量。

(3)

(4)

公式(3)、(4)中时间间隔[dkrf，dk,r+1,f]期间到达的乘客数量按照公式(5)、(6)计算，公式(6)表示第k个车站从最后一辆列车发出后到达的乘客数量。

(5)

(6)

公式(3)中列车从k站出发时刻的站台上没有上车的乘客数量按照公式(7)、(8)计算，即为想要上车的乘客数量减去考虑列车运力后实际上车的乘客数量。

(7)

(8)

此外，当列车从第k个车站离开时列车上的乘客数量可以使用公式(9)、(10)计算，一辆车从车站出发后的载客量等于其到达时的载客量加上上车乘客减去下车乘客。

(9)

(10)

上车的乘客数量计算分两种情况，当候车乘客数量大于车上剩余位置时，上车的乘客数量等于列车上的剩余位置，否则等于候车的乘客数量也就是说候车的乘客都能上车。

(11)

(12)

在前文计算得到行车计划的基础上，将乘客在站台的等待时间分为四部分，第一部分为由于列车满员未能上车的乘客的等待时间，第二部分是在两辆服务列车运行间隔期间到达的乘客的等待时间，第三部分是指第一辆车到达车站之前乘客的等待时间，第四部分是列车服务结束后到规划期结束之前乘客的等待时间。

(13)

可以为线路提供服务的列车数量是有限的，因此这个问题的主要解决方案是优化所有列车的发车时间以及到达时间。利用表1～3的变量和参数，列车时刻表优化模型需要满足以下约束：

(14)

(15)

(16)

(17)

(18)

(19)

约束(14)是最小以及最大车头时距限制，结合《地铁设计规范》[13]对于城市轨道交通列车高峰和平峰的运行间隔的规定，为了保证列车运行的安全性，列车运行时的车头时距不能小于最小追踪间隔hmin=2 min，最大运行间隔为hmax=10 min。约束(15)保证列车在计划期内发车的均衡性。在不同的阶段，列车发车时间的跳跃性可增长乘客的出行时间，列车的发车间隔应保证均衡性[14]，其中α∈[0,1]，β∈[0,1]。约束(16)规定了列车在车站的停留时间，列车的停车时间等于列车离开站台的时刻减去列车到达站台的时刻，列车在站台上的停留时间太短会导致乘客无法顺利上车，停留时间过长则会增加乘客的旅行时间，因此列车在站台上的停靠时间应该控制在合理的范围内。约束(17)规定了列车的折返作业组织，说明了起始站的发车时间与对向列车的到达时间以及折返作业时间相关，在服务列车数量有限的情况下，如果列车晚点，可能造成整个线路的列车运行发生故障。约束(18)为车站空余约束，假设除折返站外其余车站每次只能停一辆列车，该约束保证车站只有不大于一辆列车停靠。约束(19)为运营时间约束，第r列列车在第f方向列车从k站行驶到k+1站的时间为Rkf。

2 遗传和声算法

传统的遗传算法在优化大规模不规则问题时，计算时间长，难以实现全局搜索，给求解造成一定困难。Geem[15]受协调乐队演奏出音乐的启发，抽象出一种新的启发式智能算法——和声算法，具有概念简单、可调参数少、容易实现的特点，并成功应用于函数优化问题，但取值概率以及微调概率的不同对求解过程以及结果影响较大，求解复杂问题容易陷入局部最优。为了优化两种算法的缺点，本文将遗传算法和和声算法组合并优化，优化后算法稳定性强，比原算法跳出局部最小的能力强[12]。将问题的求解分成以下两个部分：运用遗传算法求得一组列车到达始发站时刻和停站时间，作为和声初始库输入和声算法进行求解；再运用和声搜索机制在得到的始发站时刻和停站时间的次优种群中进行搜索微调，获得更优的列车时刻表。

具体算法求解步骤如下，求解逻辑图如图3所示。

图3 算法逻辑图

步骤1：初始化算法参数。设定最大遗传代数、种群规模、交叉变异概率、和声记忆库大小、和声保留概率、音调微调概率、扰动带宽、和声迭代次数。

步骤2：编码。染色体由车辆到达始发站时间和列车在站台停靠时间两部分组成。根据计划期以及列车服务总次数Df生成所有方向的列车到达始发站时刻的初始编码；根据各区间列车最大停靠时间和最小停靠时间为界限随机生成列车在站台停靠时间编码。

步骤3：选择操作。根据得到的每一个列车在初始站到达时刻和停站时刻组结合路段运行时间，计算乘客在站台等待的时间，根据得到的等待时间的倒数分配个体被选择的比例，随机选择，更新种群。

步骤4：交叉操作。将染色体片段分为列车始发站到达时刻片段和列车停站时间片段，随机选择两个父代个体，选择基因起止位置，选择方式为随机选择，交换这两组基因的位置。进行冲突监测，监测列车始发站到达时刻片段是否出现重复整数，是否满足列车追踪间隔约束，保证子代基因无冲突。比较交叉前后个体的适应度大小，将较优个体加入到子代。

步骤5：变异操作。经过多次计算尝试，本文变异参数p的取值范围为0.05～0.20。与交叉操作类似，将染色体片段划分为列车始发站到达时刻片段和列车停站时间片段。列车到达始发站时刻组是一组升序自然数，列车在站停车时间组是一组最大和最小停站时间范围内的随机自然数，因此，对前者基因片段采用均匀变异法，对后者采用插入变异法，验证变异后的染色体片段是否满足优化问题中的约束条件，满足则将变异后的个体遗传到下一代。

步骤6：遗传算法结束条件。若迭代次数小于最大遗传代数，进行步骤7，否则返回步骤3。

步骤7：生成新和声。步骤6得到的次优种群输入为和声算法的和声库，一系列列车到达时刻和停站时间，通过随机选择、和声保留、扰动原则等3个原则产生新解，扰动原则为Xnew=X+2LbwR-Lbw，其中，X表示解的集合，R是0和1之间的随机数，Lbw是扰动带宽。

步骤8：更新记忆库。根据步骤7得到新的时刻表，验证得到的时刻表是否满足以上模型的约束条件，满足则求乘客站台等待时间，将其与原来最长等待时间比较，若小于则替换，和声记忆库更新。

步骤9：和声算法终止条件。迭代次数是否小于最大迭代次数，否则返回步骤7，是则输出求解的较优列车到达始发站时刻和列车停车间隔时间，转化为优化后的最终的列车时刻表。

3 算例分析

本文以图4所示的单线循环的线路为例，共有2×5个相互独立的车站。循环线路分成两个方向：f=1表示上行方向；f=2表示下行方向。两条线路相互独立，不存在乘客换乘。为了验证本文所提方法的正确性及模型的效果，两端都有车辆段可以发车，列车从1车站发车后，经过车站2、3、4后在车站5进行折返并从另一方向的车站1继续发车，研究时间段为5400 s。

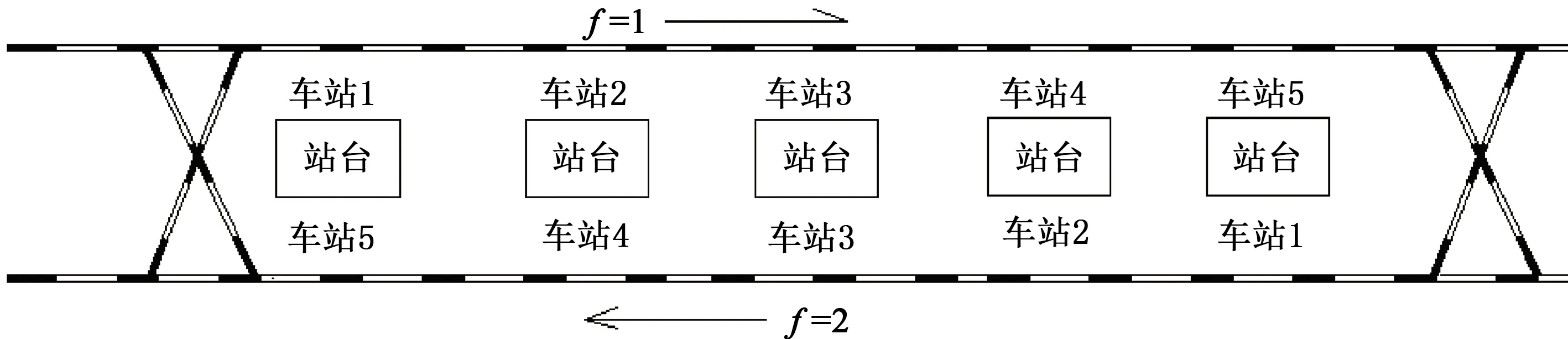
图4 算例示意图

3.1 参数设置

列车的各项基本参数如表3所示。

表3 列车运行基础参数

遗传和声算法参数包括种群规模100、交叉概率0.7、变异概率0.2、最大遗传代数600、和声记忆库大小100、和声迭代次数600、和声保留概率0.95、音调调节率0.3和扰动带宽0.2。

OD矩阵(origin-destination matrix)又名起讫点矩阵，其中“O”指出行的出发地点，“D”指出行的目的地，直观简洁地表示了从一个地点向另一个地点转移的客流数量。本文轨道交通线路上的乘客出行OD矩阵如表4所示。

表4 乘客出行OD矩阵

3.2 计算结果

根据上述参数和约束条件，使用遗传算法和遗传和声算法分别计算得到的9次较优解的结果以及平均值，见表5。

表5 遗传算法与遗传和声算法计算人均候车时间对比

通过表5的对比可以直观地看出，遗传算法共搜索到了3次较优解，人均等待时间为1141 s/人，9次较优解的平均值为1 152.6 s/人。而遗传和声算法共搜索到了7次较优解1141 s/人，9次较优解的平均值为1 144.6 s/人。结果表明，遗传和声算法相较遗传算法计算结果更加准确，跳出局部最小的能力更强，体现了遗传和声算法的应用价值。

在按照客流需求给出行车计划后，用Matlab设计的遗传和声算法求解列车时刻表优化模型得到较优解。图5是根据解所绘制的列车运行图，优化结果符合列车运行安全等约束。

图5 列车运行图

4 结论

本文根据客流需求计算行车计划，将行车计划结果用于列车时刻表的优化模型，并采用遗传和声算法求解优化问题，提高了求解效率和准确性。最后通过算例分析，得到了符合实际且合理的列车时刻表。在未来的工作中，将进一步研究混合编组、跨站停车、快慢车等复杂条件下行车计划的制定和列车运行时刻表的优化问题，并进一步验证遗传和声算法求解这类复杂问题的合理性和准确性。