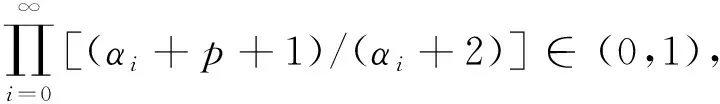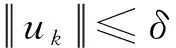Schrödinger-Bopp-Podolsky方程多重负能量解的存在性
2020-12-30朱玉婷陈春芳
朱玉婷,陈春芳
(南昌大学理学院,中国 南昌 330031)
2019年,d’Avenia和Siciliano考虑在Bopp-Podolsky电磁理论[1]中,将薛定谔场Ψ=Ψ(t,x)与其电磁场相结合,并研究静电场情况下驻波问题,首次提出如下Schrödinger-Bopp-Podolsky系统:
(1)
其中a,ω>0,q≠0,并得到以下结论:
(i)若a,ω>0,p∈(2,6),则当|q|足够小时问题(1)存在非平凡解;
(ii)若a,ω>0,p∈(3,6)则对任意的q≠0,问题(1)存在非平凡解;
(iii)问题(1)存在径向解,且当a→0时,该径向解趋于如下经典薛定谔泊松方程的径向解
此外,文章中还证明了K(x-x0)是方程-Δφ+a2Δ2φ=4πδx0的基本解,其中
进而有φuΔK*u2是方程-Δφ+a2Δ2φ=4πu2在空间D上的唯一解。
更多有关算子-Δ+a2Δ2的内容可参见文献[2]。算子-Δ+a2Δ2还岀现于很多物理问题与数学问题中,见文献[3-6]。在文献[7]中,Gaetano和Kaye对文献[2]的结果进行了进一步的补充与完善得到了问题(1)解的个数与q取值之间的关系。
在文献[8]中,陈思彤和唐先华研究了如下带有位势函数V(x)的Schrödinger-Bopp-Podolsky系统:
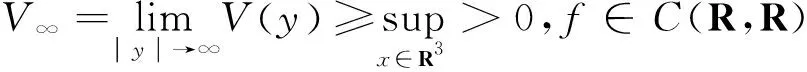
目前可见文献中,对Schrödinger-Bopp-Podolsky系统的研究多集中于非平凡解的存在性与基态解的存在性, 研究其多解的文献尚不多见。2015年,Liu[10]等人对文献[9]中所给出的Clark定理进行了完善,得到了如下扩展的Clark定理。
定理1[10]设X是一个Banach空间,Φ∈C1(X,R)。假设Φ满足(PS)条件,且有:
(i)Φ(u)=Φ(-u),Φ(0)=0且Φ有下界;
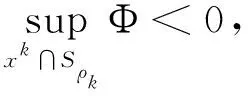
则以下结论中至少有一条成立:
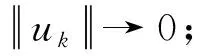
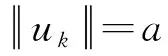
基于此,本文希望利用扩展的Clark定理,研究如下非线性Schrödinger-Bopp-Podolsky系统的负能量解的多重性。
(2)
其中a>0,V(x),Q(x)>0。对V(x),Q(x),f(x,u)做如下假设:

(V2) 存在常数do>0使得对任意正数A,有
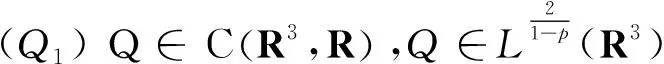
(fl) 存在δ>0,0
(f2) 在一些球Br(xo)内,有下面等式一致成立:
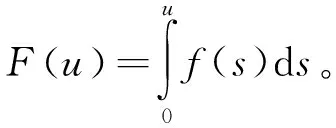
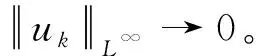
1 预备知识
本节先来介绍变分框架及一些重要结论。本文的工作空间是
内积为
范数为
引理1[1]假设(V1)- (V2)成立,则当s∈[2,6]时,E连续嵌入Ls(R3);当s∈[2,6)时,E紧嵌入Ls(R3)。
1.1 算子-Δ+a2Δ2
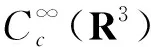
显然,D连续嵌入D1,2(R3)且连续嵌入L6(R3)。
引理2[2]K*f是方程-Δφ+a2Δ2φ=4πf的解。此外,
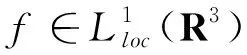
由上述引理可知,对任意u∈H1(R3),K*u2是问题(2)中第二个方程在空间D中的非平凡解,且有以下引理成立。
引理3[2]对任意u∈H1(R3),有以下结论成立:
(i) 对任意y∈R3,有φu(·+y)=φu(·+y);
(ii)φu≥0;
(iii)对任意s∈(3,+∞],有φu∈Ls(R3)∩C0(R3);
(v)φu∈D;
(vii)φu是下面方程的唯一最优解
(viii)若在空间H1(R3)中vn弱收敛于v,那么在空间D中φvn弱收敛于φv。
1.2 变分框架
下面,在E×D中定义一个能量泛函:
若(u,φ)∈E×D是泛函R的一个临界点,对任意v∈E有:
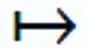
GΦ={(u,φ)∈E×D:∂uR(u,φ)=0}且Φ∈C1(E,D)。
因此,在空间E中得到如下泛函:
对任意u,v∈E,下面等式成立:
I′(u)[v]=∂uR(u,Φ(u))[v]+∂φR(u,Φ(u))°Φ′(u)[v]=∂uR(u,Φ(u))[v]
显然,研究方程(2)的解的问题可以转化为研究泛函I的临界点问题。
2 定理证明
为了得到问题(2)无穷多个负能量解的存在性,考虑如下系统
(3)
其对应能量泛函为
下面证明问题(3)具有无穷多负能量解。
因此, 由引理4知:
(4)
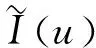
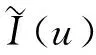

当R→∞且n→∞时, 有
故n→∞时,有:
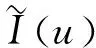
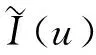
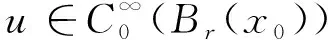
因此,得到
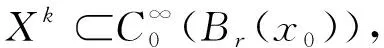
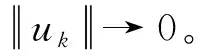
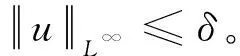
假设u为系统(3)的解, 记uM(x):=max {-M,min{u(x),M}}, 其中α>0且M>0。 由问题(3)中第一个等式,可以得到:
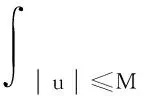
从而可以得到:
且
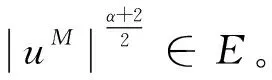
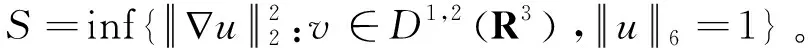
令α0=5-p,αk=3αk-1+5-p。 利用迭代法可以得到:
当k→∞时, 可得