碟形越浪式波能发电装置的三维数值模拟

刘大方,刘 臻,张国梁

(中国海洋大学 工程学院,山东 青岛266100)

目前世界上具有代表性的越浪式波浪能发电装置大多为欧洲国家所研发[1],如1985年挪威波能公司(Norwave A.S.)在挪威MOWC 电站附近建造了一座渐缩水道式波能电站[2],该电站的装机容量为350 k W,其经济效益良好,每度电成本仅为4美分,低于该岛上的柴油发电成本,这表明了利用波浪能发电装置为偏远海岛地区供电的可能性。瑞典开发了一种离岸越浪式波能发电装置——漂浮式波能船[3],该装置因具有特殊的锚固系统使其船体正对来波方向,其波能装换效率较高。丹麦所开发的龙式波能发电装置[4]由曲线型发射壁、双曲面型引浪面、漂浮式蓄水池和水轮机组组成,2个大型的曲线型引浪面使其获得了更高的捕能效率,且该装置可以很好地适应不同极端海况。

碟形越浪式波能发电装置[5]作为一种新型的越浪式波能发电装置,主要由碟形引浪面、蓄水池、导流叶片和出水管四部分组成,其结构形式较简单,可靠性较高,可以适应于不同的复杂海域和偏远海岛,且可以将不稳定的入射波能转化为较为稳定的电能,其波能转换效率较高。目前国内的学者对碟形越浪式波能装置的越浪机理和越浪性能进行了大量的物理模型试验和数值模拟研究,也对碟形越浪式波能发电装置进行了系统探索。Liu等[6]在中国海洋大学波浪水槽中进行了物理模型试验,得出了安装导流叶片以及采用较小的坡度可以显著提高装置的越浪量,并且在较小的波高和周期的条件下,导流叶片的安装角度对越浪过程也会产生较大的影响。刘娅君[7]通过二维数值模拟,进一步研究得出了干舷高度越大越浪量越小,且长周期波的越浪性能优于短周期波的结论,并通过物理试验和数值模拟相结合的方法对装置的形状进行了进一步优化[8],同时,对比轴流桨叶式水轮机和曲面叶片式水轮机,认为轴流桨叶式水轮机整体工作性能优于曲面叶片式水轮机。

碟形越浪装置还存在许多未探索和需优化的内容,且针对碟形越浪装置的数值模拟研究大多为二维数值模拟研究,而二维数值模拟存在一定的片面性和不全面性,很难反映实际情况,本文采用三维数值模拟研究方法,以碟形越浪式波能发电装置为研究对象,在规则波条件下,采用不同干舷高度和波高周期组合,进行装置的主要结构参数(包括坡度、导流叶片个数)对碟形装置的越浪性能的影响研究,得到装置的最优结构参数,进而优化碟形装置。

1 三维数值波浪水槽

1.1 控制方程

建立三维数值波浪水槽,造波板位于水槽的左侧,产生的波浪由左向右传播,消波区域位于水槽的右侧(图1)。

本文所建立的三维数值波浪水槽的顶部边界为压力出口边界条件,造波板边界、消波区边界、水槽底部和边壁均选择为壁面边界条件。在三维数值模拟研究中,通常无需考虑液体的压缩性,但需考虑液体的黏性,其控制方程为连续性方程和雷诺时均方程:

图1 三维数值波浪水槽及计算域Fig.1 Three-dimensional numerical wave flume and its computational domain

式中:x,y,z和u,v,w为坐标轴的方向和速度在该方向上的分量;υ为运动黏滞系数;ρ为流体的密度,p为流体的压强,f x,f y,f z为质量力在该方向上的分量。

本文采用VOF水气两相模型[7],该方法基于分数函数的思想:定义水的体积函数为C,在一个空间单元网格中,若C=0,则该空间单元内全部为气相;若C=1,则该空间单元内全部为水相;若0＜C＜1,则该空间单元内为水气两相自由交界面。

1.2 数值方法

本次数值模拟采用的造波技术为推板造波,因为推板造波较其他造波原理简单,易于设置。造波板的运动方程:

式中:S为冲程;ω=2π/T为入射波频率。消波区采用对规则波消波较好的Sommerfeld辐射条件,将水平速度赋予消波区,检测每个空间单元网格的水相体积分数。若水面上升,则消波区边界外移;若下降,则内移,保持该区域的水位始终保持在静水位来达到消波效果。本次数值模拟过程中的造波和消波均采用用户自定义函数(UDF)完成。模型的建立和网格的划分采用专业的前处理器ANSYS ICEM CFD 16.0,为更好地检测水气两相自由交界面处的变化,减少波浪前进过程中产生的误差,对自由水面处的网格进行加密处理。

本次数值模拟采用的离散化方法为有限体积法,为提高计算效率,求解方法选择PISO 算法进行压力-速度耦合计算,湍流模型选择RNG K-Epsilon[8]模型。

1.3 波浪水槽的验证

图2 碟形越浪装置的基本参数Fig.2 Basic parameters of the circular ramp overtopping wave energy convertor

为验证本文所构建的三维数值波浪水槽的可靠性,对碟形越浪式波能发电装置进行数值模拟,并对比模拟结果与物理试验结果[9]。碟形越浪装置的主要结构参数如图2所示,其中Rc为干舷高度,Dm为蓄水池直径,Db为装置底盘直径,Df为装置吃水线长度,Hr为蓄水池高度,α为坡度角。入射波选择线性规则波,坡度比S=1∶1.25,干舷高度Rc=0.1 m,共计算了12组规则波工况(表1),其中H为波高,T为周期。

在本次数值模拟研究中,对每一种工况进行至少10个波浪的检测,以保证数值模拟的结果的准确性。评价装置的越浪性能的主要参数指标是进入蓄水池的越浪量,为消除在模拟过程中波高的影响,对单宽越浪量q进行无量纲计算:

本文构建的三维数值波浪水槽的模拟结果与试验结果的相互比较如图3所示。物理模型试验与数模的越浪状态图对比如图4所示。

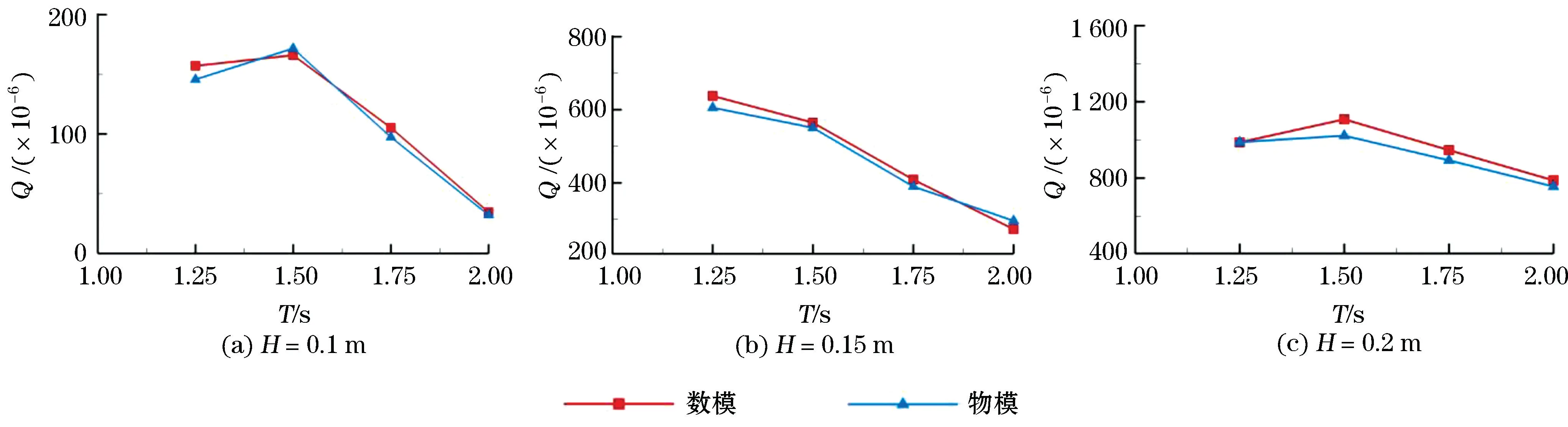
图3 试验与数值模拟无量纲越浪量对比Fig.3 Comparison of dimensionless overtopping rates obtained by testing and numerically simulating

图4 物理模型试验结果(左)与数模越浪状态(右)对比Fig.4 Comparison of the wave overtopping states obtained by physical model testing(left)and numerically simulating(right)

图3给出了在不同波高周期条件下数值模拟结果和试验结果的无量纲越浪量的对比,由于数值模拟中的流量损失误差较少且无外界因素的影响,数值模拟结果略大于物模结果,其总体误差约为8%。如图4所示,在一个周期的越浪过程中,本文中数值模拟的越浪状态图与试验的越浪状态图吻合良好且总体趋势相同,所构建的三维数值波浪水槽能够准确模拟越浪现象,并能够准确预测碟形越浪装置的越浪量。因此本文所构建的三维数值波浪水槽达到计算要求。

2 不同参数对越浪性能的影响

为研究碟形越浪装置的最优结构参数(包括坡度比、导流叶片个数和干舷高度),以三维碟形越浪装置数值模型为研究对象,在规则波条件下,采用2组干舷高度,3组波高和4组波周期组合,分析结构参数对越浪性能的影响。

2.1 坡度比

装置的坡度比对越浪性能有着一定的影响,在蓄水池高度确定的情况下,坡度比也决定了装置的引浪面长度,为探索坡度比对装置越浪性能的影响,本次数值模拟研究采用4种不同的坡度比分别为:S=1∶1.25,S=1∶1.50,S=1∶1.75,S=1∶2.00。在干舷高度Rc=0.1 m、导流叶片个数为0的条件下进行了12组规则波的数值模拟,其数值模拟结果如图5所示。

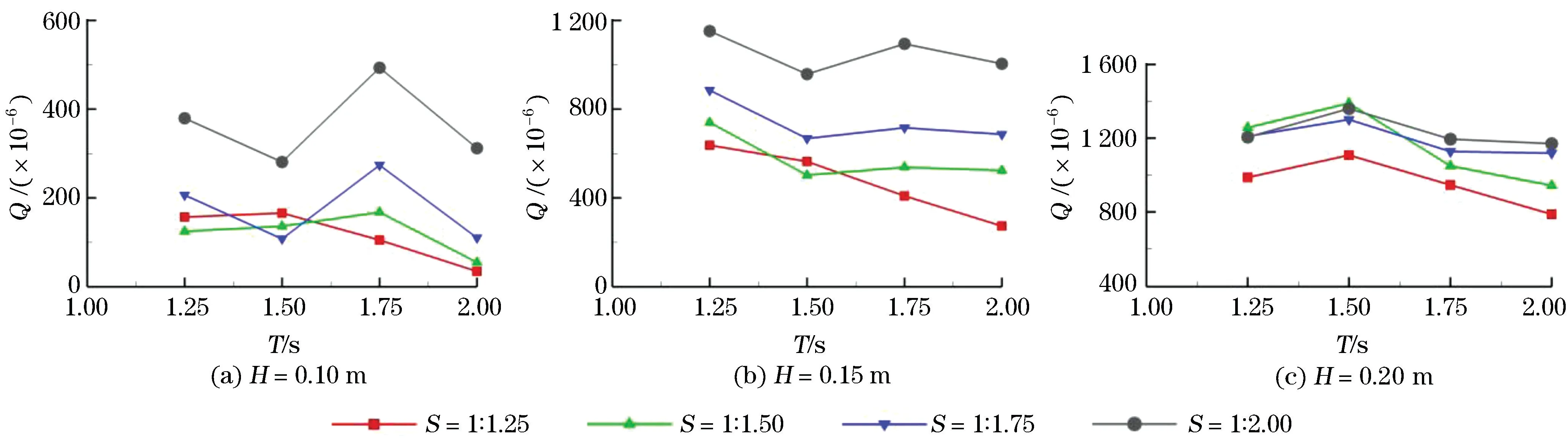
图5 不同坡度比的越浪量对比Fig.5 Comparison of the overtopping rates with different slope ratios

由图5可知,当波高H=0.10和0.15 m 时,坡度比S=1∶2.00的越浪量明显高于其他3种坡度比;当H=0.20 m 时坡度比S=1∶2.00与S=1∶1.75,S=1∶1.50的越浪量相差不大。综上所述,在本次数值模拟条件下,当坡度比S=1∶2.00时,装置的越浪量最大,装置的越浪效果最为良好,可作为该条件下的最优坡度比的选择。

2.2 导流叶片个数

导流叶片的存在有利于回收原本会回落海中的水体并顺着导流叶片进入蓄水池内。本次三维数值模拟计算中选择了3种不同导流叶片个数分别为0,6和12,在干舷高度Rc=0.1 m、坡度比S=1∶2.00条件下进行了12组规则波的数值计算,其数值模拟结果见图6。图6为在相同波高周期条件下的不同导流叶片个数的无量纲越浪量的对比,当导流叶片个数为12时,其越浪量明显优于6叶片和0叶片,所以装置设置12导流叶片能更好限制水体滑落,同时抬高波浪增大越浪量,其越浪性能最好。所以12导流叶片可作为装置的最优选择。

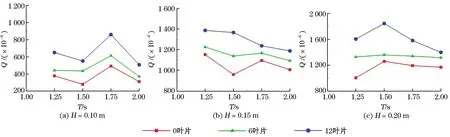
图6 不同导流叶片的越浪量对比Fig.6 Comparison of the overtopping rates with different numbers of diversion blades

2.3 干舷高度

不同的干舷高度也会影响装置的越浪量,本次三维数值模拟给出了2种不同的干舷高度,分别为:Rc=0.10和0.15 m,在坡度比S=1∶2,导流叶片为0的条件下,进行12组规则波的数值计算,结果见图7。由图7可知,在波高周期一定的情况下,干舷高度越大,装置的越浪量越小,其越浪性能越差,所以在实际海况中,应当使装置保持一个较小的干舷高度以确保有足够的越浪量带动水轮机的运转。

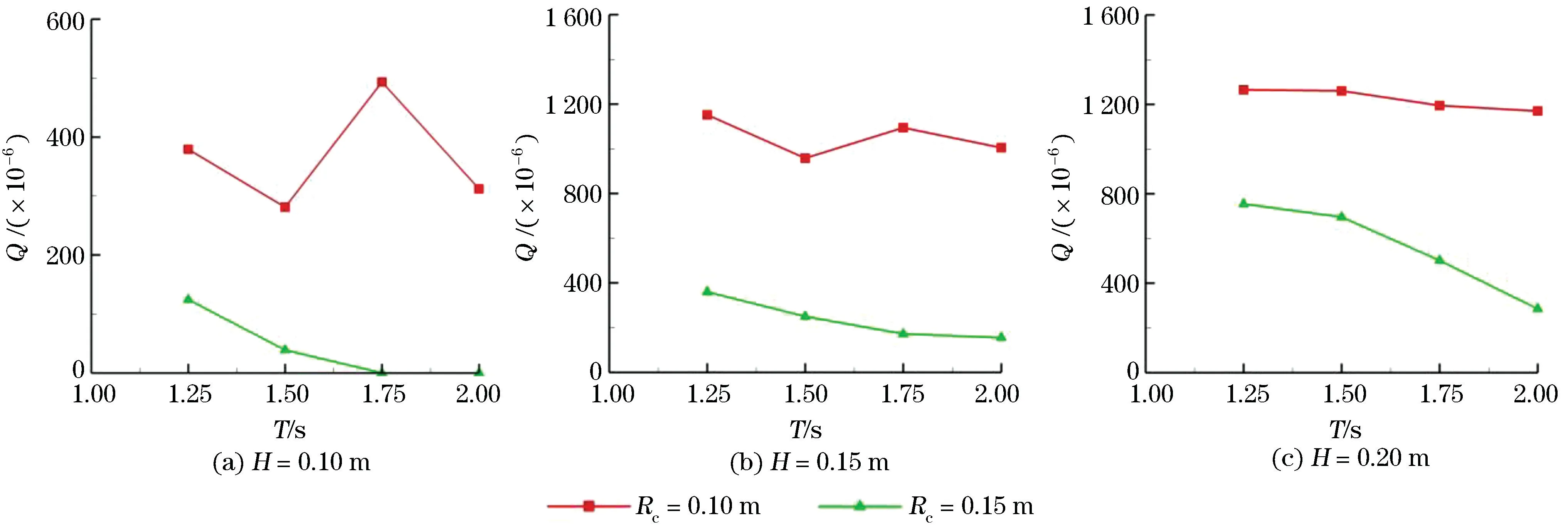
图7 不同干舷高度的越浪量对比Fig.7 Comparison of the overtopping rates with different freeboard heights

3 优化设计

在对碟形装置的三维数值模拟中,通过观察其越浪过程发现波浪在爬坡过程,若没能跃进蓄水池,波浪会顺着斜坡形成回流阻碍后面的波浪前进。为减少波浪回流,在碟形装置的斜坡面边缘加上回流板以达到优化效果(图8),回流板长度为D。为探索回流板对碟形越浪装置有无优化影响,在坡度比S=1∶2,干舷高度Rc=0.1 m 的条件下对带有回流板的装置进行12组规则波的数值模拟,其与原装置的越浪量对比见图9。

图8 优化后碟形越浪装置Fig.8 The circular ramp overtopping wave energy convertor after the optimization

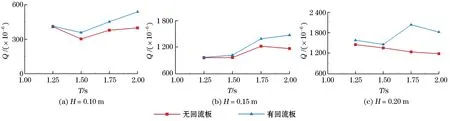
图9 有无回流板的越浪量对比Fig.9 Comparison of the overtopping rates with and without backflow plate

由图9可知,当周期T=1.25和1.50 s时,回流板对装置的优化效果较小,优化效果约在7%左右,当周期T=1.75,2.00 s时,回流板对装置的优化效果较好,优化效果约在30%左右。总体来说,带有回流板的碟形越浪装置的越浪量大于原装置,其越浪性能优于原装置,所以回流板对碟形装置具有一定的优化作用。

现探索回流板的长度对装置的优化效果的影响,本次研究给出3种不同的回流板长度分别为D=0.10,0.15和0.20 m,在坡度比S=1∶2,导流叶片为0的条件下,进行12组规则波的数值计算,其3种不同长度的越浪量对比结果见图10。

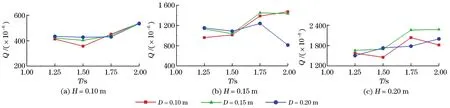
图10 不同回流板长度的越浪量对比Fig.10 Comparison of the overtopping rates with different backflow plate lengths

由图10可知,当波高H=0.1 m 时,3种不同长度的回流板的优化效果相差不大,当波高H=0.15 m 和H=0.2 m 时,在周期T=1.25 s时与T=1.50 s时D=0.15 m 与D=0.20 m 的越浪量较优于D=0.10 m时的越浪量;当T=1.75 s时与T=2.00 s时,D=0.15 m 时的越浪量较优于D=0.10 m 与D=0.20 m 的越浪量。综上所述,回流板长度设为0.15 m 时的优化效果最为良好。

4 结 论

构建了基于VOF模型的三维数值波浪水槽,并对碟形越浪装置进行了数值模拟计算,此三维数值波浪水槽可准确模拟越浪现象,可用于碟形越浪装置的模拟和优化计算。

在不同的波高、周期和干舷高度组合条件下对碟形越浪装置的主要结构参数进行了三维数值模拟计算,并对碟形装置进行了优化设计和数值模拟,得到了以下结论:

1)当坡度比S增大时,装置的越浪量随之增大,坡度比S=1∶2时装置的越浪性能最为良好,当导流叶片个数增多时,装置的越浪量随之增大,当导流叶片为12时装置的越浪性能最为良好。

2)装置的越浪量随着干舷高度的增大而减小,在实际海况中,装置应保持一个较小的干舷高度以保证其良好的越浪性能。

3)带有回流板的碟形装置的越浪性能有明显的提高,当回流板长度增大时,装置的越浪量有先增大后减小的趋势,当回流板长度D=0.15 m 时装置的越浪性能最为良好。